Exercise 1.5 & 1.6 - Real Numbers RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Exercise - 1.5
Question: 1
Show that the following numbers are irrational.
(i) 7 √5
(ii) 6 + √2
(iii) 3 - √5
Solution:
(i) Let us assume that 7 √5 is rational. Then, there exist positive co primes a and b such that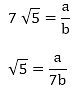
We know that √5 is an irrational number
Here we see that √5 is a rational number which is a contradiction.
(ii) Let us assume that 6+√2 is rational. Then, there exist positive co primes a and b such that
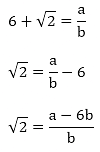
Here we see that √2 is a rational number which is a contradiction as we know that √2 is an irrational number
Hence 6 + √2 is an irrational number
(iii) Let us assume that 3 - √5 is rational. Then, there exist positive co primes a and b such that
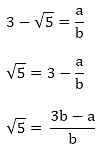
Here we see that √5 is a rational number which is a contradiction as we know that √5 is an irrational number
Hence 3 - √5 is an irrational number.
Question: 2
Prove that the following numbers are irrationals.
(i) 2√7
(ii) 3/(2√5)
(iii) 4 + √2
(iv) 5√2
Solution:
(i) Let us assume that 2√7 is rational. Then, there exist positive co primes a and b such that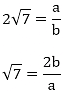
√7 is rational number which is a contradiction
Hence 2√7 is an irrational number
(ii) Let us assume that 3/(2√5) is rational. Then, there exist positive co primes a and b such that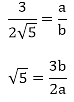
√5 is rational number which is a contradiction
Hence 3/(2√5) is irrational.
(iii) Let us assume that 3/(2√5) is rational. Then, there exist positive co primes a and b such that

√2 is rational number which is a contradiction
Hence 4+ √2 is irrational.
(iv) Let us assume that 5√2 is rational. Then, there exist positive co primes a and b such that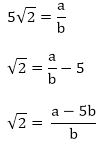
√2 is rational number which is a contradiction
Hence 5√2 is irrational
Question: 3
Show that 2 - √3 is an irrational number.
Solution:
Let us assume that 2 - √3 is rational. Then, there exist positive co primes a and b such that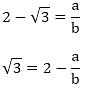
Here we see that √3 is a rational number which is a contradiction
Hence 2- √3 is irrational
Question: 4
Show that 3 + √2 is an irrational number.
Solution:
Let us assume that 3 + √2 is rational. Then, there exist positive co primes a and b such that
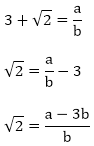
Here we see that √2 is a irrational number which is a contradiction
Hence 3 + √2 is irrational
Question: 5
Prove that 4 - 5√2 is an irrational number.
Solution:
Let us assume that 4 - 5√2 is rational. Then, there exist positive co primes a and b such that
This contradicts the fact that √2 is an irrational number
Hence 4 – 5√2 is irrational
Question: 6
Show that 5 - 2√3 is an irrational number.
Solution:
Let us assume that 5 -2√3 is rational. Then, there exist positive co primes a and b such that
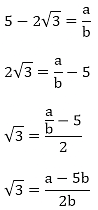
This contradicts the fact that √3 is an irrational number
Hence 5 – 2√3 is irrational
Question: 7
Prove that 2√3 - 1 is an irrational number.
Solution:
Let us assume that 2√3 – 1 is rational. Then, there exist positive co primes a and b such that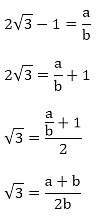
This contradicts the fact that √3 is an irrational number
Hence 5 - 2√3 is irrational
Question: 8
Prove that 2 - 3√5 is an irrational number.
Solution:
Let us assume that 2 - 3√5 is rational. Then, there exist positive co primes a and b such that

This contradicts the fact that √5 is an irrational number
Hence 2 - 3√5 is irrational
Question: 9
Prove that √5 + √3 is irrational.
Solution:
Let us assume that √5 + √3 is rational. Then, there exist positive co primes a and b such that
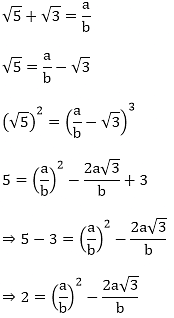
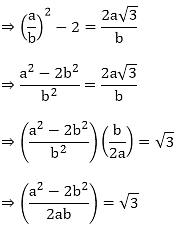
Here we see that √3 is a rational number which is a contradiction as we know that √3 is an irrational number
Hence √5 + √3 is an irrational number
Question: 10
Prove that √3 + √4 is irrational.
Solution:
Let us assume that √3 + √4 is rational. Then, there exist positive co primes a and b such that

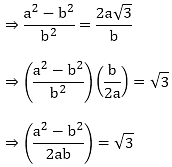
Here we see that √3 is a rational number which is a contradiction as we know that √3 is an irrational number
Hence √3 + √4 is an irrational number
Question: 11
Prove that for any prime positive integer p, √p is an irrational number.
Solution:
Let us assume that √p is rational. Then, there exist positive co primes a and b such that
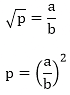
⇒ pb2 = a2
⇒ p|a2 ⇒ p|a2
⇒ p|a ⇒ p|a
⇒ a = pc for some positive integer c ⇒ a = pc for some positive integer c
b2p = a2
⇒ b2p = p2c2 ( ∵ a = pc)
⇒ p|b2 (since p|c2p) ⇒ p|b2(since p|c2p)
⇒ p|b ⇒ p|a and p|b
This contradicts the fact that a and b are co primes
Hence √p is irrational
Question: 12
If p, q are prime positive integers, prove that √p + √q is an irrational number.
Solution:
Let us assume that √p + √q is rational. Then, there exist positive co primes a and b such that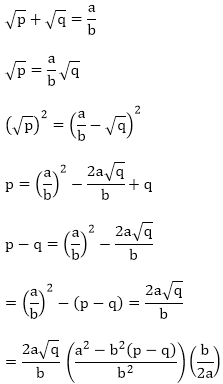
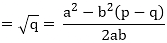
Here we see that √q is a rational number which is a contradiction as we know that √q is an irrational number
Hence √p + √q is an irrational number
Exercise - 1.6
Question: 1
Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
(i) 23/8
(ii) 125/441
(iii) 35/50
(iv) 77/210
(v) 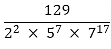
Solution:
(i) The given number is 23/8
Here, 8 = 23 and 2 is not a factor of 23.
So, the given number is in its simplest form.
Now, 8 = 23 is of the form 2m × 5n, where m = 3 and n = 0.
So, the given number has a terminating decimal expansion.
(ii) The given number is 125/441
Here, 441 = 32 × 72 and none of 3 and 7 is a factor of 125.
So, the given number is in its simplest form.
Now, 441 = 32 × 72 is not of the form 2m × 5n
So, the given number has a non-terminating repeating decimal expansion.
(iii) The given number is 35/50 and HCF (35, 50) = 5.
Here, 7/10 is in its simplest form.
Now, 10 = 2 × 5 is of the form 2m × 5n, where in = 1 and n = 1.
So, the given number has a terminating decimal expansion.
(iv) The given number is 77/210 and HCF (77, 210) = 7.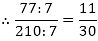
Here, 11/30 is in its simplest form. 30
Now, 30 = 2 × 3 × 5 is not of the form 2m × 5n.
So, the given number has a non-terminating repeating decimal expansion.
(v) The given number is  Clearly, none of 2, 5 and 7 is a factor of 129.
Clearly, none of 2, 5 and 7 is a factor of 129.
So, the given number is in its simplest form.
Question: 2
Write down the decimal expansions of the following rational numbers by writing their denominators in the form of 2m × 5n, where m, and n, are the non- negative integers.
(i) ⅜
(ii) 13/125
(iii) 7/80
(iv) 14588/625
(v) 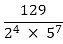
Solution.
(i) The given number is ⅜
Clearly, 8 = 23 is of the form 2m × 5n, where m = 3 and n = 0.
So, the given number has terminating decimal expansion.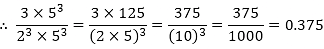
(ii) The given number is 13/125
Clearly, 125 = 53 is of the form 2m × 5n, where m = 0 and n = 3.
So, the given number has terminating decimal expansion.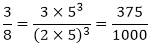
(iii) The given number is 7/80.
Clearly, 80 = 24 × 5 is of the form 2m × 5n, where m = 4 and n = 1.
So, the given number has terminating decimal expansion.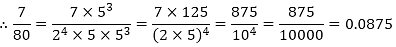
(iv) The given number is 14588/625
Clearly, 625 = 54 is of the form 2m × 5n, where m = 0 and n = 4.
So, the given number has terminating decimal expansion?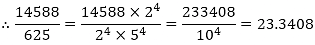
(v) The given number is 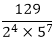 Clearly, 22 × 57 is of the form 2m × 5n, where in = 2 and n = 7.
Clearly, 22 × 57 is of the form 2m × 5n, where in = 2 and n = 7.
So, the given number has terminating decimal expansion?
Question: 3
What can you say about the prime factorization of the denominators of the following rational?
(i) 43.123456789
(ii) 
(iii) 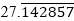
(iv) 0.120120012000120000
Solution.
(i) Since 43.123456789 has terminating decimal expansion. So, its denominator is of the form 2m × 5n, where m, n are non-negative integers.
(ii) Since 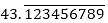 has non-terminating decimal expansion. So, its denominator has factors other than 2 or 5.
has non-terminating decimal expansion. So, its denominator has factors other than 2 or 5.
(iii) Since 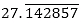 has non-terminating decimal expansion. So, its denominator has factors other than 2 or 5.
has non-terminating decimal expansion. So, its denominator has factors other than 2 or 5.
(iv) Since 0.120120012000120000 … has non-terminating decimal expansion. So, its denominator has factors other than 2 or 5.
|
5 videos|292 docs|59 tests
|
FAQs on Exercise 1.5 & 1.6 - Real Numbers RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are the properties of real numbers? |  |
| 2. What is the difference between rational and irrational numbers? |  |
| 3. How can real numbers be represented on a number line? |  |
| 4. How do you determine if a number is rational or irrational? |  |
| 5. What are the different types of real numbers? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|

















