Exercise 1.1
Question: 1
If a and b are two odd positive integers such that a > b, then prove that one of the two numbers  and
and  is odd and the other is even.
is odd and the other is even.
Solution:
Given: If a and b are two odd positive integers such that a > b.
To Prove: That one of the two numbers  and
and  is odd and the other is even.
is odd and the other is even.
Proof: Let a and b be any odd positive integer such that a > b. Since any positive integer is of the form q, 2q + 1
Let, a = 2q + 1 and b = 2m + 1, where, q and in are some whole numbers

Which is a positive integer.

Given, a > b
2q + 1 > 2m + 1
2q > 2m
q > m
Therefore,

Thus,  is a positive integer.
is a positive integer.
We need to prove that one of the two numbers  and
and  is odd and other is even.
is odd and other is even.
Consider, 
Also, we know that from the proof above that

are positive integers.
We know that the difference of two integers is odd if one of them is odd and another is even. (Also, the difference between two odd and two even integers is even)
Hence it is proved that if a and b are two odd positive integers is even.
Hence, it is proved that if a and b are two odd positive integers such that a > b then one of the two number  and
and  is odd and the other is even.
is odd and the other is even.
Question: 2
Prove that the product of two consecutive positive integers is divisible by 2.
Solution:
To Prove: that the product of two consecutive integers is divisible by 2.
Proof: Let n – 1 and n be two consecutive positive integers.
Then their product is n (n – 1) = n2 – n
We know that every positive integer is of the form 2q or 2q + 1 for some integer q.
So let n = 2q
So, n2 – n = (2q)2 – (2q)
n2 – n = (2q)2 – (2q)
n2 – n = 4q2 – 2q
n2 – n = 2q (2q – 1)
n2 – n = 2r [where r = q(2q – 1)]
n2 – n is even and divisible by 2
Let n = 2q + 1
So, n2 – n = (2q + 1)2 – (2q + 1)
n2 – n = (2q + 1) (2q + 1) – 1)
n2 – n = (2q + 1) (2q)
n2 – n = 2r[r = q (2q + 1)]
n2 – n is even and divisible by 2
Hence it is proved that the product of two consecutive integers is divisible by 2.
Question: 3
Prove that the product of three consecutive positive integers is divisible by 6.
Solution:
To Prove: the product of three consecutive positive integers is divisible by 6.
Proof: Let n be any positive integer. Since any positive integer is of the form 6q or 6q + 1 or 6q + 2 or 6q + 3 or 6q + 4, 6q + 5.
If n = 6q, n(n + 1)(n + 2) = 6q(6q + 1)(6q + 2), which is divisible by 6
If n = 6q + 1, n(n + 1)(n + 2) = (6q + 1)(6q + 2)(6q + 3) n(n + 1)(n + 2) = 6 (6q + 1)(3q + 1)(2q + 1) Which is divisible by 6
If n = 6q + 2, n(n + 1)(n + 2) = (6q + 2)(6q + 3)(6q + 4) n(n + 1)(n + 2) = 12(3q + 1)(2q + 1)(2q + 3),
Which is divisible by 6.
Similarly, we can prove others.
Hence it is proved that the product of three consecutive positive integers is divisible by 6.
Question: 4
For any positive integer n, prove that n3 – n divisible by 6.
Solution:
To Prove: For any positive integer n, n3 — n is divisible by 6.
Proof: Let n be any positive integer. n3 — n = (n – 1)(n)(n + I)
Since any positive integer is of the form 6q or 6q + 1 or 6q + 2 or 6q + 3 or 6q + 4, 6q + 5
If n = 6q,
Then, (n —1)n(n + 1) = (6q —1)6q (6q + 1)
Which is divisible by 6
If n = 6q + 1,
Then, (n —1)n(n + 1) = (6q)(6q + 1)(6q + 2)
Which is divisible by 6.
If n = 6q + 2,
Then, (n – 1)n(n + 1) = (6q + 1)(6q + 2)(6q + 3)
(n – 1)n(n + 1) = 6(6q + 1)(3q + 1)(2q + 1)
Which is divisible by 6.
Similarly, we can prove others.
Hence it is proved that for any positive integer n, n3— n is divisible by 6.
Question: 5
Prove that if a positive integer is of form 6q + 5, then it is of the form 3q + 2 for some integer q, but not conversely.
Solution:
To Prove: If a positive integer is of the form 6q + 5 then it is of the form 3q + 2 for some integer q, but not conversely.
Proof: Let n = 6q + 5
Since any positive integer n is of the form of 3k or 3k + 1, 3k + 2
If q = 3k,
Then, n = 6q + 5
n = 18k + 5 (q = 3k)
n = 3(6k + 1) + 2
n = 3m + 2 (where m = (6k + 1))
If q = 3k+ 1,
Then, n = (6q + 5)
n = (6 (3k + 1) + 5)(q = 3k + 1)
n = 18k + 6 + 5
n = 18k + 11
n = 3(6k + 3) + 2
n = 3m + 2 (where m = (6k + 3))
If q = 3k + 2,
Then, n = (6q + 5)
n = (6(3k + 2) + 5)(q = 3k + 2)
n = 18k + 12 + 5
n = 18k + 17
n = 3(6k + 5) + 2
n = 3m + 2 (where m = (6k + 5))
Consider here 8 which is the form 3q + 2 i.e. 3 × 2 + 2 but it can’t be written in the form 6q + 5. Hence the converse is not true.
Question: 6
Prove that any square of any positive integer of the form 5q + 1 is of the same form.
Solution:
To Prove: That the square of a positive integer of the form 5q + 1 is of the same form
Proof: Since positive integer n is of the form 5q + 1
If n = 5q + 1
Then n2 = (5q + 1)2
n2 = (5q)2 + 2 (1) (5q) + 12 = 25q2 + 10q + 1
n2 = 5m + 1 (where m = (5q2 + 2q))
Hence n2 integer is of the form 5m + 1.
Question: 7
Prove that the square of any positive integer is of form 3m or 3m + 1 but not of form 3m + 2.
Solution:
To Prove: that the square of a positive integer is of form 3m or 3m + 1 but not of form 3m + 2.
Proof: Since positive integer n is of the form of 3q , 3q + 1 and 3q + 2
If n = 3q
n2 = (3q)2
n2 = 9q2
n2 = 3 (3q)2
n2 = 3m(m = 3q)2
If n = 3q + 1
Then, n2 = (3q + 1)2
n2 = (3q)2 + 6q + 1
n2 = 9q2 + 6q + 1
n2 = 3q(3q + 1) + 1
n2 = 3m +1(where m = (3q + 2))
If n = 3q + 2
Then, n2 = (3q + 2)2 = (3q)2 + 12q + 4
n2 = 9q2 + 12q + 4
n2 = 3 (3q + 4q + 1) + 1
n2 = 3m + 1 (where q = (3q + 4q + 1)
Hence, n2 integers are of the form 3m, 3m + 1 but not of the form 3m + 2.
Question: 8
Prove that the square of any positive integer is of the form 4q or 4q + 1 for some integer q.
Solution:
To Prove: The square of any positive integer is of the form 4q or 4q + 1 for some integer q.
Proof: Since positive integer n is of the form of 2q or 2q + 1
If n = 2q
Then, n2 = (2q)2
n2 = 4q2
n2 = 4m (where m = q2)
If n = 2q + 1
Then, n2 = (2q + 1)2
n2 = (2q)2 + 4q + 1
n2 = 4q2 + 4q + 1
n2 = 4q (q + 1) + 1
n2 = 4q + 1 (where m = q (q + 1))
Hence it is proved that the square of any positive integer is of the form 4q or 4q + 1, for some integer q.
Question: 9
Prove that the square of any positive integer is of the form 5q or 5q + 1, 5q + 4 for some integer q.
Solution:
To Prove: The square of any positive integer is of the form 5q or 5q + 1, 5q + 4 for some integer q.
Proof: Since positive integer n is of 5q or 5q + 1, 5q + 4.
If n = 5q, Then. n2 = (5q)2
n2 = 25q2
n2 = 5 (5q)
n2 = 5m (Where m = 5q)
If n = 5q + 1
Then, n2 = (5q +1)2
n2 = (5q)2 + 10q + 1
n2 = 25q2 + 10q + 1
n2 = 5q (5q + 2) + 1
It n2 = 5q (5q +2) + 1
n2 = 5m +1 (where m = q (5q + 2))
If n = 5q + 2
Then, n2 = (5q + 2)2
n2 = (5q)2 + 20q + 4
n2 = 25q2 + 20q + 4
n2 = 5q (5q + 4) + 4
n2 = 5m + 4 (where m = q (5q + 4))
If n = 5q + 4
Then, n2 = (5q + 4)2
n2 = (5q)2 + 40q + 16
n2 = 25q2 + 40q + 16
n2 = 5 (5q2 + 8q + 3) + 1
n2 = 5m + 1 (where m = 5q2 + 8q + 3 )
Hence it is proved that the square of any positive integer is of the form 5q or 5q + 1, 5q + 4 for some integer q.
Question: 10
Show that any positive odd integer is from 6q +1 or 6q + 3 or 6q + 5, where q is some integer.
Solution:
To Prove: the square of any positive integer is of the form 8q + 1 for some integer q.
Proof: Since any positive integer n is of the form 4m + 1 and 4m + 3
If n = m + 1
Then,
n2 = (4m + 1)2
n2 = (4m)2 + 8m + 1
n2 = 16m2 + 8m + 1
n2 = 8m (2m + 1) + 1
n2 + 8q +1 (where q = m (2m + 1))
If n = 4m + 3
Then, n2 = (4m + 3)2
n2 = (4m)2 + 24m + 9
n2 = 16m2 + 24m + 9
n2 = 8 (2m2 + 3m + 1) + 1
n2 = 8q + 1 (where q = (2m2 + 3m + 1))
Hence, n2 integers are of the form 8q + 1, for some integer q.
Question: 11
Show that any positive odd integer is from 6q +1 or 6q + 3 or 6q + 5, where q is some integer.
Solution:
To Show: Any positive odd integer is of the form 6q + 1 or 6q + 3 or 6q + 5 where q is any integer.
Proof: Let ‘a’ be any odd positive integer and b = 6.
Then, there exists integers q and r such that a = 6q + r, 0 ≤ r < 6 (by division algorithm)
a = 6q or 6q + 1 or 6q + 2 or 6q + 3 or 6q + 4
But 6q or 6q + 2 or 6q + 4 are even positive integers.
So, a = 6q + 1 or 6q + 3 or 6q + 5
Hence it is proved that any positive odd integer is of the form 6q + 1 or 6q + 3 or 6q + 5, where q is an integer.
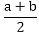 and
and 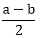 is odd and the other is even.
is odd and the other is even. and
and 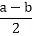 is odd and the other is even.
is odd and the other is even.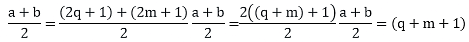


 is a positive integer.
is a positive integer. and
and 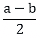 is odd and other is even.
is odd and other is even.
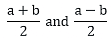
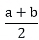 and
and  is odd and the other is even.
is odd and the other is even.
























