Real Numbers - 2 RD Sharma Solutions | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Exercise 1.2 |

|
| Exercise: 1.3 |

|
| Exercise - 1.4 |

|
| Exercise - 1.5 |

|
| Exercise - 1.6 |

|
Exercise 1.2
Question: 1
Define HCF of two positive integers and find the HCF of the following pairs of number:
(i) 32 and 54
(ii) 18 and 24
(iii) 70 and 30
(iv) 56 and 88
(v) 475 and 495
(vi) 75 and 243
(vii) 240 and 6552
(viii) 155 and 1385
(i×) 100 and 190
(×) 105 and 120
Solution:
(i). We need to find H.C.F. of 32 and 54.
By applying division lemma 54 = 32 × 1 + 22
Since remainder ≠ 0, apply division lemma on 32 and remainder 22
32 = 22 × 1 + 10
Since remainder ≠ 0, apply division lemma on 22 and remainder 10
22 = 10 × 2 + 2
Since remainder ≠ 0, apply division lemma on 10 and 2
10 = 2 × 5 + 0
Therefore, H.C.F. of 32 and 54 is
(ii) We need to find H.C.F. of 18 and 24.
By applying division lemma
24 = 18 × 1 + 6.
Since remainder ≠ 0, apply division lemma on divisor 18 and remainder 6
18 = 6 × 3 + 0.
Therefore, H.C.F. of 18 and 24 is 6
(iii) We need to find H.C.F. of 70 and 30.
By applying Euclid's Division lemma
70 = 30 × 2 + 10.
Since remainder ≠ 0, apply division lemma on divisor 30 and remainder 10
30 = 10 × 3 + 0.
Therefore, H.C.F. of 70 and 30 = 10
(iv) We need to find H.C.F. of 56 and 88.
By applying Euclid's Division lemma
88 = 56 × 1 + 32.
Since remainder ≠ 0, apply division lemma on 56 and remainder 32
56 = 32 × 1 + 24.
Since remainder ≠ 0, apply division lemma on 32 and remainder 24
32 = 24 × 1+ 8.
Since remainder ≠ 0, apply division lemma on 24 and remainder 8
24 = 8 × 3 + 0. Therefore, H.C.F. of 56 and 88 = 8
(v) We need to find H.C.F. of 475 and 495.
By applying Euclid’s Division lemma,
495 = 475 × 1 + 20.
Since remainder ≠ 0, apply division lemma on 475 and remainder 20
475 = 20 × 23 + 15.
Since remainder ≠ 0, apply division lemma on 20 and remainder 15
20 = 15 × 1 + 5.
Since remainder ≠ 0, apply division lemma on 15 and remainder 5
15 = 5 × 3 + 0.
Therefore, H.C.F. of 475 and 495 = 5
(vi) We need to find H.C.F. of 75 and 243.
By applying Euclid's Division lemma
243 = 75 × 3 + 18.
Since remainder ≠ 0, apply division lemma on 75 and remainder 18
75 = 18 × 4 + 3.
Since remainder ≠ 0, apply division lemma on divisor 18 and remainder 3
18 = 3 × 6 + 0.
Therefore, H.C.F. of 75 and 243 = 3
(vii) We need to find H.C.F. of 240 and 6552.
By applying Euclid's Division lemma
6552 = 240 × 27 + 72.
Since remainder ≠ 0, apply division lemma on divisor 240 and remainder 72
240 = 72 × 3 + 24.
Since remainder ≠ 0, apply division lemma on divisor 72 and remainder 24
72 = 24 × 3 + 0.
Therefore, H.C.F. of 240 and 6552 = 24
(viii) We need to find H.C.F. of 155 and 1385.
By applying Euclid's Division lemma
1385 = 155 × 8 + 145.
Since remainder ≠ 0, apply division lemma on divisor 155 and remainder 145.
155 = 145 × 1 + 10.
Since remainder ≠ 0 apply division lemma on divisor 145 and remainder 10
145 = 10 × 14 + 5.
Since remainder ≠ 0, apply division lemma on divisor 10 and remainder 5
10 = 5 × 2 + 0.
Therefore, H.C.F. of 155 and 1385 = 5
(ix) We need to find H.C.F. of 100 and 190.
By applying Euclid's division lemma
190 = 100 × 1 + 90.
Since remainder ≠ 0, apply division lemma on divisor 100 and remainder 90
100 = 90 × 1 + 10.
Since remainder ≠ 0, apply division lemma on divisor 90 and remainder 10
90 = 10 × 9 + 0.
Therefore, H.C.F. of 100 and 190 = 10
(x) We need to find H.C.F. of 105 and 120.
By applying Euclid's division lemma
120 = 105 × 1 + 15.
Since remainder ≠ 0, apply division lemma on divisor 105 and remainder 15
105 = 15 × 7 + 0.
Therefore, H.C.F. of 105 and 120 = 15.
Question: 2
Use Euclid's division algorithm to find the HCF of
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255
Solution:
(i) Given integers are 225 and 135.
Clearly 225 > 135.
So we will apply Euclid's division lemma to 225 and 135, we get,
867 = (225) (3) + 192
Since the remainder ≠ 0. So we apply the division lemma to the divisor 135 and remainder 90. We get,
135 = (90) (1) + 45
Now we apply the division lemma to the new divisor 90 and remainder 45. We get,
90 = (45) (2) + 0
The remainder at this stage is 0. So the divisor at this stage is the H.C.F.
So, the H.C.F of 225 and 135 is 45
(ii) Given integers are 38220 and 196. Clearly 38220 > 196.
So we will apply Euclid's division lemma to 38220 and 196, we get,
38220 = (196)(195) + 0
The remainder at this stage is 0. So the divisor at this stage is the H.C.F.
So the H.C.F of 38220 and 196 is 196
(iii) Given integers are 867 and 255. Clearly 867 > 225.
So we will apply Euclid's division lemma to 867 and 225, we get,
867 = (225)(3) + 192
Since the remainder 192 ≠ 0. So we apply the division lemma to the divisor 225 and remainder 192. We get,
225 = (192)(1) + 33
Now we apply the division lemma to the new divisor 192 and remainder 33. We get,
192 = (33)(5) + 27
Now we apply the division lemma to the new divisor 33 and remainder 27. We get,
33 = (27)(1) + 6
Now we apply the division lemma to the new divisor 27 and remainder 6. We get,
27 = (6)(4) + 3
Now we apply the division lemma to the new divisor 27 and remainder 6. We get,
6 = (3) (2) + 0
The remainder at this stage is 0. So the divisor at this stage is the H.C.F.
So the H.C.F of 867 and 255 is 3.
Question: 3
Find the HCF of the following pair of integers and express it as a linear combination of them,
(i) 963 and 657
(ii) 592 and 252
(iii) 506 and 1155
(iv) 1288 and 575
Solution:
(i) We need to find the H.C.F. of 963 and 657 and express it as a linear combination of 963 and 657. By applying Euclid’s division lemma, 963 = 657 × 1 + 306.
Since remainder ≠ 0, apply division lemma on divisor 657 and remainder 306
657 = 306 × 2 + 45.
Since remainder ≠ 0, apply division lemma on divisor 306 and remainder 45
306 = 45 × 6 + 36.
Since remainder ≠ 0, apply division lemma on divisor 45 and remainder 36
45 = 36 × 1 + 9.
Since remainder ≠ 0, apply division lemma on divisor 36 and remainder 9
36 = 9 × 4 + 0.
Therefore, H.C.F. = 9.
Now, 9 = 45 – 36 × 1
= 45 – [306 – 45 × 6] × 1 = 45 – 306 × 1 + 45 × 6
= 45 × 7 – 306 × 1 = [657 - 306 × 2] × 7 – 306 × 1
= 657 × 7 – 306 × 14 – 306 × 1
= 657 × 7 – 306 × 15
= 657 × 7 – [963 – 657 × 1] × 15
= 657 × 7 – 963 × 15 + 657 × 15
= 657 × 22 – 963 × 15.
Hence, obtained.
(ii) We need to find the H.C.F. of 592 and 252 and express it as a linear combination of 592 and 252.
By applying Euclid's division lemma
592 = 252 × 2 + 88
Since remainder ≠ 0, apply division lemma on divisor 252 and remainder 88
252 = 88 × 2 + 76
Since remainder ≠ 0, apply division lemma on divisor 88 and remainder 76
88 = 76 × 1 + 12
Since remainder ≠ 0, apply division lemma on divisor 76 and remainder 12
76 = 12 × 6 + 4
Since remainder ≠ 0, apply division lemma on divisor 12 and remainder 4
12 = 4 × 3 + 0.
Therefore, H.C.F. = 4.
Now, 4 = 76 – 12 × 6
= 76 – 88 – 76 × 1 × 6
= 76 – 88 × 6 + 76 × 6
= 76 × 7 – 88 × 6
= 252 – 88 × 2 × 7 – 88 × 6
= 252 × 7- 88 × 14 - 88 × 6
= 252 × 7- 88 × 20
= 252 × 7 – 592 – 252 × 2 × 20
= 252 × 7 – 592 × 20 + 252 × 40
= 252 × 47 – 592 × 20
= 252 × 47 + 592 × (-20)
Hence obtained.
(iii) We need to find the H.C.F. of 506 and 1155 and express it as a linear combination of 506 and 1155. By applying Euclid's division lemma
1155 = 506 × 2 + 143.
Since remainder ≠ 0, apply division lemma on divisor 506 and remainder 143
506 = 143 × 3 + 77.
Since remainder ≠ 0, apply division lemma on divisor 143 and remainder 77
143 = 77 × 1 + 66.
Since remainder ≠ 0, apply division lemma on divisor 77 and remainder 66
77 = 66 × 1 + 11.
Since remainder ≠ 0, apply division lemma on divisor 66 and remainder 11
66 = 11 × 6 + 0.
Therefore, H.C.F. = 11.
Now, 11 = 77 – 66 × 1 = 77—[143 – 77 × 1] × 1
= 77 – 143 × 1 + 77 × 1
= 77 × 2 – 143 × 1
= [506 – 143 × 3] × 2 – 143 × 1
= 506 × 2 – 143 × 6 – 143 × 1
= 506 × 2 – 143 × 7 = 506 × 2 – [1155 – 506 × 2] × 7 = 506 × 2 – 1155 × 7+ 506 × 14
= 506 × 16 – 1155 × 7
Hence obtained.
(iv) We need to find the H.C.F. of 1288 and 575 and express it as a linear combination of 1288 and 575. By applying Euclid's division lemma
1288 = 575 × 2 + 138.
Since remainder ≠ 0, apply division lemma on divisor 506 and remainder 143
575 = 138 × 4 + 23.
Since remainder ≠ 0, apply division lemma on divisor 143 and remainder 77
138 = 23 × 6 + 0.
Therefore, H.C.F. = 23.
Now, 23 = 575 – 138 × 4 = 575—[1288 – 575 × 2] × 4
= 575 – 1288 × 4 + 575 × 8
Hence, obtained.
Question: 4
Find the largest number which divides 615 and 963 leaving remainder 6 in each case.
Solution:
We need to find the largest number which divides 615 and 963 leaving remainder 6 in each case.
The required number when divides 615 and 963, leaves remainder 6, this means 615 — 6 = 609 and 963 — 6 = 957 are completely divisible by the number.
Therefore,
The required number = H.C.F. of 609 and 957.
By applying Euclid’s division lemma
957 = 609 × 1+ 348
609 = 348 × 1 + 261
348 = 216 × 1 + 87
261 = 87 × 3 + 0.
Therefore, H.C.F. = 87.
Hence, the required number is 87
Question: 5
If the HCF of 408 and 1032 is expressible in 1032 m – 408 × 5, find m.
Solution:
We need to find m if the H.C.F of 408 and 1032 is expressible in the form 1032 m — 408 × 5
Given integers are 408 and 1032 where 408 < 1032
By applying Euclid’s division lemma, we get 1032 = 408 × 2 + 216.
Since the remainder ≠ 0, so apply division lemma on divisor 408 and remainder 216
408 = 216 × 1 + 192.
Since the remainder ≠ 0, so apply division lemma on divisor 216 and remainder 192
216 = 192 × 1 + 24.
Since the remainder ≠ 0, so apply division lemma on divisor 192 and remainder 24
192 = 24 × 8 + 0.
We observe that remainder is 0. So the last divisor is the H.C.F of 408 and 1032.
Therefore,
24 = 1032 m — 408 × 5
1032 m = 24 + 408 × 5
1032 m = 24 + 2040
1032 m = 2064
m = 2064/1032
m = 2
Therefore, m = 2.
Question: 6
If the HCF of 657 and 963 is expressible in the form 657x + 963x – 15, find x.
Solution:
We need to find x if the H.C.F of 657 and 963 is expressible in the form 657x + 963y (-15).
Given integers are 657 and 963.
By applying Euclid's division lemma, we get,
963 = 657 × 1+ 306.
Since the remainder ≠ 0, so apply division lemma on divisor 657 and remainder 306
657 = 306 × 2 + 45.
Since the remainder ≠ 0, so apply division lemma on divisor 306 and remainder 45
306 = 45 × 6 + 36.
Since the remainder ≠ 0, so apply division lemma on divisor 45 and remainder 36
45 = 36 × 1 + 9.
Since the remainder ≠ 0, so apply division lemma on divisor 36 and remainder 9
36 = 9 × 4 + 0.
Therefore, H.C.F. = 9.
Given H.C.F = 657x + 936 (-15).
Therefore, 9 = 657x —14445
9 + 14445 = 657x
14454 = 657x
x = 14454/657
On solving the above, we have,
x = 22.
Hence obtained.
Question: 7
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to in the same number of columns. What is the maximum number of columns in which they can march?
Solution:
We are given an army contingent of 616 members to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. We need to fund the maximum number of columns in which they can march.
Members in army = 616
Members in-band = 32.
Therefore, Maximum number of columns = H.C.F of 616 and 32.
By applying Euclid’s division lemma
616 = 32 × 19 + 8
32 = 8 × 4 + 0.
Therefore, H.C.F. = 8
Hence, the maximum number of columns in which they can march is 8
Question: 8
A merchant has 120 litres of oil of one kind, 180 litres of another and 240 litres of the third kind. He wants to sell the oil by filling the three kinds of oil in tins of equal capacity. What should be the greatest capacity of such a tin?
Solution:
The merchant has 3 different oils of 120 litres, 180 litres and 240 litres respectively.
So the tin's greatest capacity for filling three different types of oil is given by the H.C.F. of 120,180 and 240.
So first we will calculate H.C.F of 120 and 180 by Euclid's division lemma.
180 = (120)(1) + 60
120 = (60)(2) + 0
The divisor at the last step is 60. So the H.C.F of 120 and 180 is 60.
Now we will fund the H.C.F. of 60 and 240,
240 = (60)(4) + 0
The divisor at the last step is 60. So the H.C.F of 240 and 60 is 60.
Therefore, the tin should be of 160 litres.
Question: 9
During a sale, colour pencils were being sold in packs of 24 each and crayons in packs of 32 each. If you want full packs of both and the same number of pencils and crayons, how many of each would you need to buy?
Solution:
We are given that during a sale, colour pencils were being sold in packs of 24 each and crayons in packs of 32 each. If we want full packs of both and the same number of pencils and crayons, we need to find the number of each we need to buy.
Given that, Number of colour pencils in one pack = 24
The number of crayons in pack = 32.
Therefore, the least number of both colours to be purchased
L.C.M of 24 and 32 = 2 × 2 × 2 × 2 × 2 × 3 = 96
Hence, the number of packs of pencils to be bought
96/24 = 4, And a number of packs of crayon to be bought
96/32 = 3
Question: 10
144 cartons of coke cans and 90 cartons of Pepsi cans are to be stacked in a canteen. If each stack is of the same height and contains cartons of the same drink, what would be the greatest number of cartons each stack would have?
Solution:
Given that 144 cartons of coke cans and 90 cartons of Pepsi cans are stacked in a canteen. If I each stack is of the same height and contains cartons of the same drink. We need to find the greatest number of cartons, and each stack would have
Given that,
Number of cartons of coke cans = 144
A number of cartons of Pepsi cans = 90.
Therefore, the greatest number of cartons in one stack = H.C.F. of 144 and 90.
By applying Euclid’s division lemma 144 = 90 × 1 + 54
90 = 54 × 1+ 36
54 = 36 × 1 + 18
36 = 18 × 2 + 0
H.C.F. =18.
Hence, the greatest number cartons in one stack 18
Question: 11
Find the greatest number which divides 285 and 1249 leaving remainders 9 and 7 respectively.
Solution:
We need to find the greatest number which divides 285 and 1249 leaving remainder 9 and 7 respectively.
The required number when divides 285 and 1249, leaves remainder 9 and 7, this means 285 – 9 = 276 and 1249 -7 = 1242 are completely divisible by the number.
Therefore, the required number = H.C.F. of 276 and 1242.
By applying Euclid's division lemma,
1242 = 276 × 4 + 138
276 = 138 × 2 + 0.
Therefore, H.C.F. = 138
Hence, the required number is 138
Question: 12
Find the largest number which exactly divides 280 and 1245, leaving remainders 4 and 3, respectively.
Solution:
We need to find the largest number which exactly divides 280 and 1245, leaving remainders 4 and 3, respectively.
The required number when divides 280 and 1245, leaves remainder 4 and 3, this means 280 – 4 = 276 and 1245 – 3 = 1242 are completely divisible by the number.
Therefore, the required number = H.C.F. of 276 and 1242.
By applying Euclid’s division lemma 1242 = 276 × 4 + 138
276 = 138 × 2 + 0.
Therefore, H.C.F. = 138.
Hence, the required number is 138
Question: 13
What is the largest number that divides 626, 3127 and 15628 and leaves remainders of 1, 2 and 3 respectively?
Solution:
We need to find the largest number that divides 626, 3127 and 15628 and leaves remainders of 1, 2 and 3 respectively.
The required number when divides 626, 3127 and 15628 leaves remainders 1, 2 and 3 this means
626 – 1 = 625,
3127 – 2 = 3125,
And 15628 – 3 = 15625 are completely divisible by the number.
Therefore, the required number = H.C.F. of 625, 3125 and 15625.
First, we consider 625 and 3125.
By applying Euclid’s division lemma
3125 = 625 × 5 + 0.
H.C.F. of 625 and 3125 = 625
Now, consider 625 and 15625.
By applying Euclid’s division lemma 15625 = 625 × 25 + O.
Therefore, H.C.F. of 625, 3125 and 15625 = 625
Hence, the required number is 625
Question: 14
Find the greatest number that will divide 445, 572 and 699, leaving remainders 4, 5 and 6 respectively.
Solution:
To find the greatest number that divides 445, 572 and 699 and leaves remainders of 4, 5 and 6 respectively. The required number when divides 445, 572 and 699 leaves remainders 4, 5 and 6 this means
445 – 4 = 441, 572 – 5 = 567 and 699 – 6 = 693 are completely divisible by the number.
Therefore, the required number = H.C.F. of 441, 567 and 693.
First, consider 441 and 567.
By applying Euclid’s division lemma
567 = 441 × 1 + 126
441 = 126 × 3 + 63
126 = 63 × 2 + 0.
Therefore, H.C.F. of 441 and 567 = 63
Now, consider 63 and 693
By applying Euclid's division lemma
693 = 63 × 11 + 0.
Therefore, H.C.F. of 441, 567 and 693 = 63
Hence, the required number is 63
Question: 15
Find the greatest number which divides 2011 and 2623, leaving remainders 9 and 5 respectively.
Solution:
To find the greatest number which divides 2011 and 2623 leaving remainder 9 and 5 respectively.
The required number when divides 2011 and 2623 leaves remainders 9 and 5 this means
2011 – 9 = 2002 and 2623 – 5 = 2618 are completely divisible by the number.
Therefore, the required number = H.C.F. of 2002 and 2618
By applying Euclid's division lemma
2618 = 2002 × 1 + 616
2002 = 616 × 3 + 154
616 = 154 × 4 + 0.
H.C.F. of 2002 and 2618 = 154
Hence, the required number is 154
Question: 16
Two brands of chocolates are available in packs of 24 and 15, respectively. If I need to buy an equal number of chocolates of both kinds, what is the least number of boxes of each kind I would need to buy?
Solution:
We are given that two brands of chocolates are available in packs of 24 and 15, respectively. If lie needs to buy an equal number of chocolates of both kinds, then find the least number of boxes of each kind he would need to buy.
Given that,
Number of chocolates of 1st brand in one pack = 24
The number of chocolates of 2nd brand in one pack = 15.
Therefore, the least number of chocolates he needs to purchase is
L.C.M. of 24 and 15 = 2 × 2 × 2 × 3 × 5 = 120
Therefore, the number of a packet of 1st brand is
120/24 = 5, And the number of the packet of 2nd brand is 120/15 = 8
Question: 17
A mason has to fit a bathroom with square marble tiles of the largest possible size. The size of the bathroom is 10ft by 8ft. What would be the size in inches of the tile required to be cut and how many such tiles are required?
Solution:
Size of bathroom = 10 ft by 8 ft = (10 × 12) inch by (8 × 12) inch = 120 inch by 96 inch
The largest size of tile required = HCF of 120 and 96 By applying Euclid's division lemma
120 = 96 × 1 + 24
96 = 24 × 4 + 0
Therefore, HCF = 24
Therefore, the Largest size of tile required = 24 inches
Question: 18
15 pastries and 12 biscuit packets have been donated for a school fete. These are to be packed in several smaller identical boxes with the same number of pastries and biscuits packets in each. How many biscuit packets and how many pastries will each box contain?
Solution:
Given:
Number of pastries = 15
Number of biscuit packets = 12
Therefore, the required no of boxes to contain equal number = HCF of 15 and 13
By applying Euclid's division lemma, 15 = 12 × 13
12 = 2 × 9 = 0
Therefore, No. of boxes required = 3
Hence each box will contain 15/3 = 5 pastries and 2/3 biscuit packs.
Question: 19
105 goats, 140 donkeys and 175 cows have to be taken across a river. There is only one boat which will have to make many trips to do so. The lazy boatman has his conditions for transporting them. He insists that he will take the same number of animals on every journey and be of the same kind. He will naturally like to take the largest possible number each time. Can you tell me how many animals went on each trip?
Solution:
Given:
Number of goats = 205
Number of donkey = 140
Number of cows = 175
Therefore, The largest number of animals in one trip = HCF of 105. 140 and 175.
First consider 105 and 140
By applying Euclid’s division lemma
140 = 105 × 1 + 35
105 = 35 × 3 + 0 4
Therefore, HCF of 105 and 140 = 35
Now consider 35 and 175
By applying Euclid’s division lemma
175 = 35 × 5 + 0
HCF of 105, 140 and 175 = 35
Question: 20
The length, breadth and height of a room are 8 m 25 cm, 6 m 75 cm and 4 m 50 cm, respectively. Determine the longest rod which can measure the three dimensions of the room exactly.
Solution:
Length of room = 8m 25 cm = 825 cm
Breadth of room = 6m 75m = 675 cm
Height of room = 4m 50m = 450 cm
The required longest rod = HCF of 825, 675 and 450
First consider 675 and 450
By applying Euclid’s division lemma
675 = 450 × 1 + 225
450 = 225 × 2 + 0
Therefore, HCF of 675 and 450 = 825
Now consider 625 and 825
By applying Euclid’s division Lemma:
825 = 225 × 3 + 150
225 = 150 × 1 + 75
150 = 75 × 2 + 0
Therefore, HCF of 825, 675 and 450 = 75
Question: 21
Express the HCF of 468 and 222 as 468x + 222y where x, y are integers in two different ways.
Solution:
We need to express the H.C.F. of 468 and 222 as 468x + 222y
Where x, y are integers in two different ways.
Given integers are 468 and 222, where 468 > 222
By applying Euclid’s division lemma, we get 468 = 222 × 2 + 24.
Since the remainder ≠ 0, so apply division lemma on divisor 222 and remainder 24
222 = 24 × 9 + 6.
Since the remainder ≠ 0, so apply division lemma on divisor 24 and remainder 6
24 = 6 × 4 + 0.
We observe that remainder is 0. So the last divisor 6 is the H.C.F. of 468 and 222 from we have
6 = 222 – 24 × 9
6 = 222 – (468 – 222 × 2) × 9
6 = 222 – 468 × 9 + 222 × 18
6 = 222 × 19 – 468 × 9 [Substituting 24 = 468 — 222 × 2]
16 = 222y + 468×, where × = – 9 and y = 19.
Hence, obtained.
Exercise: 1.3
Question: 1
Express each of the following integers as a product of its prime.
1. 420
2. 468
3. 945
4. 7325
Solution:
To express: each of the following numbers as a product of their prime factors
1. 420
420 = 2 × 2 × 3 × 5 × 7
2. 468
468 = 2 × 2 × 3 × 3 × 13
3. 945
945 = 3 × 3 × 3 × 5 × 7
4. 7325
7325 = 5 × 5 × 293
Question: 2
Determine the prime factorization of each of the following positive integer:
1. 20570
2. 58500
3. 45470971
Solution:
To Express: Each of the following numbers as a product of their prime factors.
1. 20570
20570 = 2 × 5 × 11 × 11 × 17
2. 58500
58500 = 2 × 2 × 3 × 3 × 5 × 5 × 5 × 13
3. 45470971
45470971 = 7 × 7 × 13 × 13 × 17 × 17 × 19
Question: 3
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Solution:
Why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
We can see that both the numbers have common factor 7 and 1.
7 × 11 × 13 + 13 = (77 + 1) × 13 = 78 × 13
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 = (7 × 6 × 4 × 3 × 2 + 1) × 5 = 1008 × 5
And we know that composite numbers are those numbers which have at least one more factor other than 1.
Hence after simplification we see that both numbers are even and therefore the given two numbers are composite numbers
Question: 4
Check whether 6n can end with the digit 0 for any natural number n.
Solution:
To Check: Whether 6n can end with the digit 0 for any natural number n.
We know that 6n = (2 × 3)n
6n = 2n × 3n
Therefore, prime factorization of 6n does not contain 5 and 2 as a factor together. Hence 6n can never end with the digit 0 for any natural number n.
Exercise - 1.4
Question: 1
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the integers:
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:
To Find: LCM and HCF of following pairs of integers
To Verify: L.C.M × H.C.F = product of the numbers
(i) 26 and 91
Let us first find the factors of 26 and 91
26 = 2 × 13
91= 7 × 13
L.C.M of 26, and 91 = 2 × 7 × 13
L.C.M of 26, and 91 = 182
H.C.F of 26, and 91 = 182
We know that, L.C.M × H.C.F = First number × Second number
182 × 13 = 26 × 91 = 2366 = 2366
Hence verified
(ii) 510 and 92
Let us first find the factors of 510 and 92
510 = 2 × 3 × 5 × 17
92 = 2 × 2 × 23
L.C.M of 510 and 92 = 2 × 2 × 3 × 5 × 23 × 17
L.C.M of 510 and 92 = 23460
H.C.F of 510 and 92 = 2
We know that, L.C.M × H.C.F = First Number × Second Number
23460 × 2 = 510 × 92
46920 = 46920
Hence verified.
(iii) 336 and 54
Let us first find the factors of 336 and 54
336 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7
54 = 2 × 3 × 3 ×3
L.C.M of 336 and 54 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7
L.C.M of 336 and 54 = 3024
H.C.F of 336 and 54 = 6
We know that, L.C.M × H.C.F = First Number × Second Number
3024 × 6 = 336 × 54
18144 = 18144
Hence verified
Question: 2
Find the LCM and HCF of the following integers by applying the prime factorization method:
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
(iv) 40, 36 and 126
(v) 84, 90 and 120
(vi) 24, 15 and 36
Solution:
To Find: LCM and HCF of following pairs of integers
(i) 15, 12 and 21
Let us first find the factors of 15, 12 and 21
12 = 2 × 2 × 3
15 = 3 × 5
21 = 3 × 7
L.C.M of 12, 15 and 21 = 2 × 2 × 3 × 5 × 7
L.C.M of 12, 15 and 21 = 420
H.C.F of 12, 15 and 21 = 3
(ii) 17, 23 and 29
Let us first find the factors of 17, 23 and 29
17 = 1 × 17
23 = 1 × 23
29 = 1 × 29
L.C.M of 17, 23 and 29 = 1 × 17 × 23 × 29
L.C.M of 17, 23 and 29 = 11339
H.C.F of 17, 23 and 29 = 1
(iii) 8, 9 and 25
Let us first find the factors of 8, 9 and 25
8 = 2 × 2 ×2
9 = 3 × 3
25 = 5 × 5
L.C.M of 8, 9 and 25 =23 × 32 × 52
L.C.M of 8, 9 and 25 = 1800
H.C.F of 8, 9 and 25 = 1
(iv) 40, 36 and 126
Let us first find the factors of 40, 36 and 126
40 = 23 × 5
36 = 23 × 32
126 = 2 × 3 × 3 × 7
L.C.M of 40, 36 and 126 = 23 × 32 × 5 × 7
L.C.M of 40, 36 and 126 = 2520
H.C.F of 40, 36 and 126 = 2
(v) 84, 90 and 120
Let us first find the factors of 84, 90 and 120
84 = 2 × 2 × 3 × 7
90 = 2 × 3 × 3 × 5
120 = 2 × 2 × 2 × 3 × 5
L.C.M of 84, 90 and 120 = 23 × 32 × 5 × 7
L.C.M of 84, 90 and 120 = 2520
H.C.F of 84, 90 and 120 = 6
(vi) 24, 15 and 36
Let us first find the factors of 24, 15 and 36
24 = 23 × 3
15 = 3 × 5
36 = 2 × 2 × 3 × 3
LCM of 24, 15 and 36 = 2 × 2 × 2 × 3 × 3 × 5
LCM of 24, 15 and 36 = 360
HCF of 24, 15 and 36 = 3
Question: 3
Given that HCF (306, 657) = 9, find LCM (306, 657 )
Solution:
Given:
HCF of two numbers 306 and 657 is 9
To find: LCM of number
We know that,
LCM × HCF = first number × second number
LCM × 9 = 306 × 657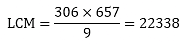
Question: 4
Can two numbers have 16 as their HCF and 380 as their as their LCM? Give reason.
Solution:
To find: can two numbers have 16 as their HCF and 380 as their LCM
On dividing 380 by 16 we get 23 as the quotient and 12 as the remainder
Since LCM is not exactly divisible by the HCF, two number cannot have 16 as their HCF and 380 as their
Question: 5
The HCF of two numbers is 145 and their LCM is 2175. If one number is 725, find the other.
Solution:
Given:
LCM and HCF of two numbers 145 and 2175 respectively.
If one number is 725
To find: other number
We know that,
LCM × HCF = first number × second number
2175 × 145 = 725 × second number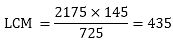
Question: 6
The HCF of two numbers is 16 and their LCM is 3072. Find the LCM.
Solution:
Given: HCF of two numbers is 16. If the product of the numbers is 3072
To find: LCM of number
We know that,
LCM × HCF = first number × second number
LCM × 16 = 3072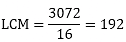
Question: 7
The LCM and HCF of two numbers are 180 and 6 respectively. If one of the numbers is 30, find the other number.
Solution:
Given:
LCM and HCF of two numbers 180 and 6 respectively.
If one number is 30
To find: other number
We know that,
LCM × HCF = First Number × Second Number
180 × 6 = 30 × Second Number

Question: 8
Find the smallest number which when increased by 17 is exactly divisible by both 520 and 468.
Solution:
To Find Smallest number which when increased by 17 is exactly divisible by both 520 and 468. L.C.M OF 520 and 468
520 = 23 × 5 × 13
468 = 2 × 2 × 3 × 3 × 13
LCM of 520 and 468 = 23 × 32 × 5 × 13 = 4680
Hence 4680 is the least number which exactly divides 520 and 468 i.e. we will get a remainder of 0 in this case. But we need the Smallest number which when increased by 17 is exactly divided by 520 and 468.
Therefore = 4680 – 17 = 46631
Hence 4663 is Smallest number which when increased by 17 is exactly divisible by both 520 and 468.
Question: 9
Find the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively.
Solution:
To Find: The smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively.
L.C.M of 28 and 32.
28 = 2 × 2 × 7
32 = 25
L.C.M of 28, and 32 = 25 × 7 = 224
Hence 224 is the least number which e×actly divides 28 and 32 i.e. we will get a remainder of 0 in this case. But we need the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively.
Therefore = 224 – 8 – 12 = 204
Hence 2041 is the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively
Question: 10
What is the smallest number that, when divided by 35, 56 and 91 leaves remainders of 7 in each case?
Solution:
To Find:
Smallest number that. When divided by 35, 56 and 91 leaves remainder of 7 in each case L.C.M OF 35, 56 and 91
35 = 5 × 7
56 = 23 × 7
91 = 13 × 7
L.C.M of 35, 56 and 91 = 23 × 7 × 5 × 13 = 3640
Hence 84 is the least number which exactly divides 28, 42 and 84 i.e. we will get a remainder of 0 in this case. But we need the smallest number that, when divided by 35, 56 and 91 leaves remainder of 7 in each case.
Therefore = 3640 + 7 = 3647
Hence 36471 is smallest number that, when divided by 35, 56 and 91 leaves remainder of 7 in each case.
Question: 11
A rectangular courtyard is 18 m 72 cm long and 13 m 20 cm broad. It is to be paved with square tiles of the same size. Find the least possible number of such tiles.
Solution:
Given: A rectangular yard is 18 m 72 cm long and 13 m 20 cm broad .It is to be paved with square tiles of the same size.
TO FIND: Least possible number of such tiles.
Length of the yard = 18 m 72 cm = 1800 cm + 72 cm = 1872 cm (therefore, 1 m = 100 cm)
Breadth of the yard = 13 in 20 cm = 1300 cm + 20 cm = 1320 cm
The size of the square tile of same size needed to the pave the rectangular yard is equals the HCF of the length and breadth of the rectangular yard.
Prime factorization of 1872 = 24 × 32 × 13
Prime factorization of 1320 = 23 × 3 × 5 × 11
HCF of 1872 and 1320 = 23 × 3 = 24
Therefore, Length of side of the square tile = 24 cm
Number of tiles required = Area of the courtyard, Area of each tile = Length × Breadth
Side2 = 1872 cm × 1320 cm 24 cm = 4290.
Thus, the least possible number of tiles required is 4290.
Question: 12
Find the greatest number of 6 digits exactly divisible by 24, 15 and 36.
Solution:
To Find:
Greatest number of 6 digits exactly divisible by 24, 15 and 36
The greatest 6 digit number be 999999 divisible by 24, 15 and 36
24 = 2 × 2 × 2 × 3
15 = 3 × 5
36 = 2 × 2 × 3 × 3
L.C.M of 24, 15 and 36 = 360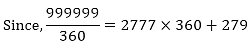
Therefore, the remainder is 279. Hence the desired number is = 999999 – 279 = 9997201
Hence 9997201 is the greatest number of 6 digits exactly divisible by 24, 15 and 36.
Question: 13
Determine the number nearest to 110000 but greater 100000 which is exactly divisible by each of 8, 15 and 21.
Solution:
To Find:
The number nearest to 110000 but greater than 100000 which is exactly divisible by each of 8, 15 and 21.
L.C.M of 8, 15 and 21.
8 = 2 × 2 × 2
15 = 3 × 5
21 = 3 × 7
L.C.M of 8, 15 and 21 =23 × 3 × 5 × 71= 840
When 110000 is divided by 840, the remainder is obtained as 800.
Now, 110000 — 800 = 109200 is divisible by each of 8, 15 and 21.
Also, 110000 + 40 = 110040 is divisible by each of 8, 15 and 21.
109200 and 110040 are greater than 100000.
Hence, 110040 is the number nearest to 110000 but greater than 100000 which is exactly divisible by each of 8, 15 and 21.
Question: 14
Find the least number that is divisible by all the numbers between 1 and 10 (both inclusive)
Solution:
To Find: Least number that is divisible by all the numbers between 1 and 10 (both inclusive) Let us first find the L.C.M of all the numbers between 1 and 10 (both inclusive)
1 = 1
2 = 2
3 = 3
4 = 2 × 2
5 = 5
6 = 2 × 3
7 = 7
8 = 2 × 2 × 2
9 = 3 × 3
10 = 2 × 5
L.C.M 2520
Hence 2520 is the least number that is divisible by all the numbers between 1 and 10 (both inclusive)
Question: 15
A circular field has a circumference of 360km. three cyclists start together and can cycle 48, 60 and 72 km a day, round the field. When will they meet again?
Solution:
Given: A circular field has a circumference of 360 km. Three cyclists start together and can cycle 48, 60, and 72 km a day, round the field.
TO FIND: When they meet again.
In order to calculate the time when they meet, we first find out the time taken by each cyclist in covering the distance.
Number of days 1st cyclist took to cover 360 km = Total distance covered in 1 day = 360/48 = 7.5 = 7510 = 152 days
Similarly, number of days taken by 2nd cyclist to cover same distance = 360/60 = 6 days
Also, number of days taken by 3rd cyclist to cover this distance = 360/72 = 5 days
Now, LCM of 152, 6 and 5 = LCM of numerators
HCF of denominators = 30/1 = 30 days
Thus, all of them will take 30 days to meet again.
Question: 16
In a morning walk three persons step off together, their steps measure 80cm, 85 cm and 90 cm respectively. What is the minimum distance each should walk so that he can cover the distance in complete steps?
Solution:
Given:
In a morning walk, three persons step off together. Their steps measure 80 cm, 85 cm and 90 cm.
To Find minimum distance each should walk so that all can cover the same distance in complete steps.
The distance covered by each of them is required to be same as well as minimum. The required distance each should walk would be the L.C.M of the measures of their steps i.e. 80 cm, 85 cm, and 90 cm,
So we have to find the L.C.M of 80 cm, 85 cm, and 90 cm.
80 = 24 × 5
85 = 17 × 5
90 = 2 × 3 × 3 × 5
L.C.M of 80, 85 and 90 = 24 × 3 × 3 × 5 × 17 = 12240 cm
Hence minimum 12240 cm distance each should walk so that all can cove the same distance in complete steps.
Exercise - 1.5
Question: 1
Show that the following numbers are irrational.
(i) 7 √5
(ii) 6 + √2
(iii) 3 - √5
Solution:
(i) Let us assume that 7 √5 is rational. Then, there exist positive co primes a and b such that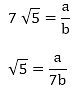
We know that √5 is an irrational number
Here we see that √5 is a rational number which is a contradiction.
(ii) Let us assume that 6+√2 is rational. Then, there exist positive co primes a and b such that
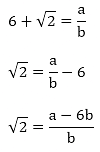
Here we see that √2 is a rational number which is a contradiction as we know that √2 is an irrational number
Hence 6 + √2 is an irrational number
(iii) Let us assume that 3 - √5 is rational. Then, there exist positive co primes a and b such that
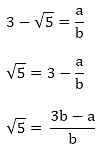
Here we see that √5 is a rational number which is a contradiction as we know that √5 is an irrational number
Hence 3 - √5 is an irrational number.
Question: 2
Prove that the following numbers are irrationals.
(i) 2√7
(ii) 3/(2√5)
(iii) 4 + √2
(iv) 5√2
Solution:
(i) Let us assume that 2√7 is rational. Then, there exist positive co primes a and b such that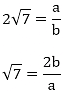
√7 is rational number which is a contradiction
Hence 2√7 is an irrational number
(ii) Let us assume that 3/(2√5) is rational. Then, there exist positive co primes a and b such that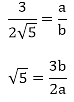
√5 is rational number which is a contradiction
Hence 3/(2√5) is irrational.
(iii) Let us assume that 3/(2√5) is rational. Then, there exist positive co primes a and b such that

√2 is rational number which is a contradiction
Hence 4+ √2 is irrational.
(iv) Let us assume that 5√2 is rational. Then, there exist positive co primes a and b such that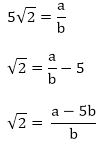
√2 is rational number which is a contradiction
Hence 5√2 is irrational
Question: 3
Show that 2 - √3 is an irrational number.
Solution:
Let us assume that 2 - √3 is rational. Then, there exist positive co primes a and b such that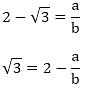
Here we see that √3 is a rational number which is a contradiction
Hence 2- √3 is irrational
Question: 4
Show that 3 + √2 is an irrational number.
Solution:
Let us assume that 3 + √2 is rational. Then, there exist positive co primes a and b such that
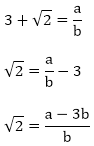
Here we see that √2 is a irrational number which is a contradiction
Hence 3 + √2 is irrational
Question: 5
Prove that 4 - 5√2 is an irrational number.
Solution:
Let us assume that 4 - 5√2 is rational. Then, there exist positive co primes a and b such that
This contradicts the fact that √2 is an irrational number
Hence 4 – 5√2 is irrational
Question: 6
Show that 5 - 2√3 is an irrational number.
Solution:
Let us assume that 5 -2√3 is rational. Then, there exist positive co primes a and b such that
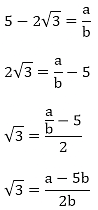
This contradicts the fact that √3 is an irrational number
Hence 5 – 2√3 is irrational
Question: 7
Prove that 2√3 - 1 is an irrational number.
Solution:
Let us assume that 2√3 – 1 is rational. Then, there exist positive co primes a and b such that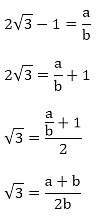
This contradicts the fact that √3 is an irrational number
Hence 5 - 2√3 is irrational
Question: 8
Prove that 2 - 3√5 is an irrational number.
Solution:
Let us assume that 2 - 3√5 is rational. Then, there exist positive co primes a and b such that

This contradicts the fact that √5 is an irrational number
Hence 2 - 3√5 is irrational
Question: 9
Prove that √5 + √3 is irrational.
Solution:
Let us assume that √5 + √3 is rational. Then, there exist positive co primes a and b such that
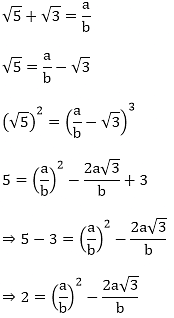
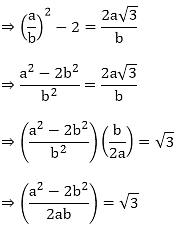
Here we see that √3 is a rational number which is a contradiction as we know that √3 is an irrational number
Hence √5 + √3 is an irrational number
Question: 10
Prove that √3 + √4 is irrational.
Solution:
Let us assume that √3 + √4 is rational. Then, there exist positive co primes a and b such that

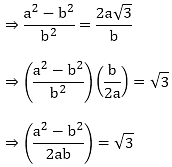
Here we see that √3 is a rational number which is a contradiction as we know that √3 is an irrational number
Hence √3 + √4 is an irrational number
Question: 11
Prove that for any prime positive integer p, √p is an irrational number.
Solution:
Let us assume that √p is rational. Then, there exist positive co primes a and b such that
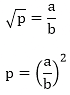
⇒ pb2 = a2
⇒ p|a2 ⇒ p|a2
⇒ p|a ⇒ p|a
⇒ a = pc for some positive integer c ⇒ a = pc for some positive integer c
b2p = a2
⇒ b2p = p2c2 ( ∵ a = pc)
⇒ p|b2 (since p|c2p) ⇒ p|b2(since p|c2p)
⇒ p|b ⇒ p|a and p|b
This contradicts the fact that a and b are co primes
Hence √p is irrational
Question: 12
If p, q are prime positive integers, prove that √p + √q is an irrational number.
Solution:
Let us assume that √p + √q is rational. Then, there exist positive co primes a and b such that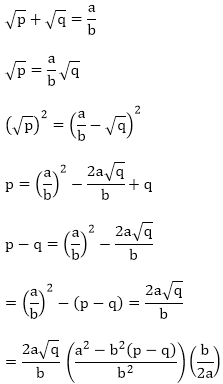
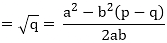
Here we see that √q is a rational number which is a contradiction as we know that √q is an irrational number
Hence √p + √q is an irrational number
Exercise - 1.6
Question: 1
Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
(i) 23/8
(ii) 125/441
(iii) 35/50
(iv) 77/210
(v) 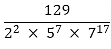
Solution:
(i) The given number is 23/8
Here, 8 = 23 and 2 is not a factor of 23.
So, the given number is in its simplest form.
Now, 8 = 23 is of the form 2m × 5n, where m = 3 and n = 0.
So, the given number has a terminating decimal expansion.
(ii) The given number is 125/441
Here, 441 = 32 × 72 and none of 3 and 7 is a factor of 125.
So, the given number is in its simplest form.
Now, 441 = 32 × 72 is not of the form 2m × 5n
So, the given number has a non-terminating repeating decimal expansion.
(iii) The given number is 35/50 and HCF (35, 50) = 5.
Here, 7/10 is in its simplest form.
Now, 10 = 2 × 5 is of the form 2m × 5n, where in = 1 and n = 1.
So, the given number has a terminating decimal expansion.
(iv) The given number is 77/210 and HCF (77, 210) = 7.
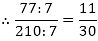
Here, 11/30 is in its simplest form. 30
Now, 30 = 2 × 3 × 5 is not of the form 2m × 5n.
So, the given number has a non-terminating repeating decimal expansion.
(v) The given number is  Clearly, none of 2, 5 and 7 is a factor of 129.
Clearly, none of 2, 5 and 7 is a factor of 129.
So, the given number is in its simplest form.
Question: 2
Write down the decimal expansions of the following rational numbers by writing their denominators in the form of 2m × 5n, where m, and n, are the non- negative integers.
(i) ⅜
(ii) 13/125
(iii) 7/80
(iv) 14588/625
(v) 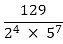
Solution.
(i) The given number is ⅜
Clearly, 8 = 23 is of the form 2m × 5n, where m = 3 and n = 0.
So, the given number has terminating decimal expansion.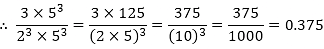
(ii) The given number is 13/125
Clearly, 125 = 53 is of the form 2m × 5n, where m = 0 and n = 3.
So, the given number has terminating decimal expansion.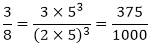
(iii) The given number is 7/80.
Clearly, 80 = 24 × 5 is of the form 2m × 5n, where m = 4 and n = 1.
So, the given number has terminating decimal expansion.
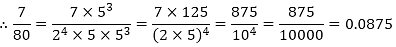
(iv) The given number is 14588/625
Clearly, 625 = 54 is of the form 2m × 5n, where m = 0 and n = 4.
So, the given number has terminating decimal expansion?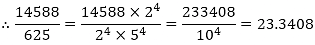
(v) The given number is 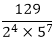 Clearly, 22 × 57 is of the form 2m × 5n, where in = 2 and n = 7.
Clearly, 22 × 57 is of the form 2m × 5n, where in = 2 and n = 7.
So, the given number has terminating decimal expansion?

Question: 3
What can you say about the prime factorization of the denominators of the following rational?
(i) 43.123456789
(ii) 
(iii) 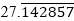
(iv) 0.120120012000120000
Solution.
(i) Since 43.123456789 has terminating decimal expansion. So, its denominator is of the form 2m × 5n, where m, n are non-negative integers.
(ii) Since 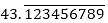 has non-terminating decimal expansion. So, its denominator has factors other than 2 or 5.
has non-terminating decimal expansion. So, its denominator has factors other than 2 or 5.
(iii) Since 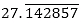 has non-terminating decimal expansion. So, its denominator has factors other than 2 or 5.
has non-terminating decimal expansion. So, its denominator has factors other than 2 or 5.
(iv) Since 0.120120012000120000 … has non-terminating decimal expansion. So, its denominator has factors other than 2 or 5.
|
126 videos|457 docs|75 tests
|
FAQs on Real Numbers - 2 RD Sharma Solutions - Mathematics (Maths) Class 10
| 1. What are real numbers? |  |
| 2. What is the importance of studying real numbers? |  |
| 3. How do we classify real numbers? |  |
| 4. What is the difference between rational and irrational numbers? |  |
| 5. How can real numbers be used in everyday life? |  |

|
Explore Courses for Class 10 exam
|

|

















