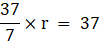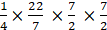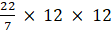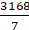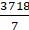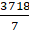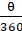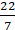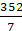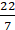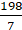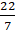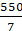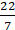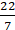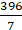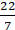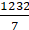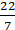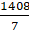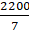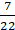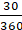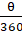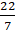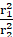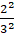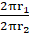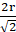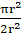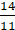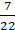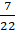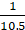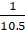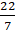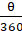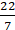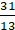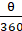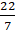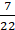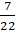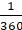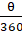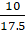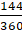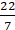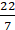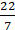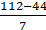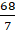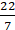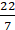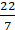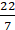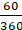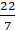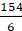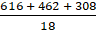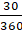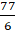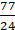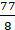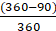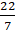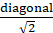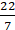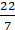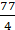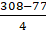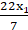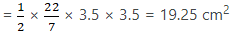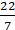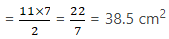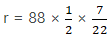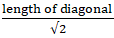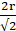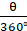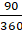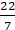RS Aggarwal Solutions: Area of Circle, Sector and Segment- 1 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download

Q.1. The difference between the circumference and radius of a circle is 37 cm. Using π = 22/7, find the circumference of the circle.

Given:
Difference between the circumference and the radius of circle = 37 cm
Let the radius of the circle be ‘r’.
Circumference of the circle = 2πr
So, Difference between the circumference and the radius of the circle = 2πr – r = 37
2πr – r = 37
2 × (22/7) × r – r = 37 
 (44/7) × r – r = 37


r = 37 × (7/37)
r = 7 cm
∴ Circumference of circle = 2 × (22/7) × 7
= 2 × 22
= 44 cm
Hence the circumference of the circle is 44 cm.

Q.2. The circumference of a circle is 22 cm. Find the area of its quadrant.

Given:
Circumference of circle = 22 cm
Let the radius of the circle be ‘r’.
∵ Circumference of circle = 2πr
∴ 22 = 2 × π × r
⇒ 22 = 2 × (22/7) × r 
⇒ 22 × (7/22) × (1/2) = r or  = r
or r = (7/2)
∵ Area of circle = πr²
∴ Area of its quadrant = (1/4)πr²
= 
= 77/8
Hence the area of the quadrant of the circle is 77/8 cm.

Q.3. What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameter 10 cm and 24 cm?

Given:
Let the two circles be C₁ and C₂ with diameters 10 cm and 24 cm respectively.
Area of circle, C = Area of C₁ + Area of C₂ …… (i)
∵ Diameter = 2 × radius
∴ Radius of C₁, r₁ = 10/2 = 5cm
and Radius of C₂, r₂ = 24/2 = 12cm
∵ Area of circle = πr² …… (ii)
∴ Area of C₁ = πr₁²
= (22/7) 5 x 5
= (22/7) x 25
= 550/7 cm²
Similarly, Area of C₂ = πr₂²
= 
= 22/7 × 144
= 3168/7 cm² 
∴ Using equation (i), we have
Area of C =  + 
=  cm² 
Now, using equation (ii), we have

 × r² = 
r² = 
r² = 169
r = 
r = 13 cm
⇒ Diameter = 2 × r
= 2 × 13
= 26 cm
Hence, the diameter of the circle is 26 cm.

Q.4. If the area of a circle is numerically equal to twice its circumference, then what is the diameter of the circle?

Given:
Area of circle = 2 × Circumference of circle …… (i)
Let the radius of the circle be ‘r’.
Then, the area of the circle = πr²
and the circumference of the circle = 2πr
Using (i), we have
πr² = 2 × 2πr
πr² = 4πr
r = 4 cm
∵ Diameter = 2 × radius
∴ Diameter = 2 × 4
= 8 cm
Hence, the diameter of the circle is 8 cm.

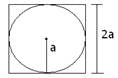
Q.5. What is the perimeter of a square which circumscribes a circle of radius a cm?

Given:
Perimeter of square circumscribes a circle of radius ‘a’.

Side of square = Diameter of circle
Diameter of circle = 2 × radius
= 2a
So, Side of square = 2a
∵ Perimeter of square = 4 × side
∴ Perimeter of square = 4 × 2a
= 8a
Hence, the perimeter of the square is 8a.

Q.6. Find the length of the arc of a circle of diameter 42 cm which subtends an angle of 60° at the centre.

Given:
Diameter of circle = 42 cm
⇒ Radius of circle = 42/2 cm = 21 cm
Angle subtended at the centre = 60°
∵ Length of arc =  × 2πr 
= 
= 22 cm
Hence, the length of the arc is 22 cm.

Q.7. Find the diameter of the circle whose area is equal to the sum of the areas of two circles having radii 4 cm and 3 cm.

Given:
Let the two circles with radii 4 cm and 3 cm be C₁ and C₂ respectively.
⇒ r₁ = 4 cm and r₂ = 3 cm
Area of circle, C = Area of C₁ + Area of C₂ …… (i)
∵ Area of circle = πr² …… (ii)
∴ Area of C₁ = πr₁²

= 
=  × 16 =  cm² 
Similarly, Area of C₂ = πr₂²
=  × 3 × 3 
=  × 9 =  cm² 
So, using (i), we have
Area of C =  +  =  cm² 
Now, using (ii), we have
πr² = 550/7
 × r² = 
r² =  ×  = 25 
r = √25 = 5
r = 5 cm
∵ Diameter = 2 × radius
∴ Diameter = 2 × 5 = 10 cm
Hence, diameter of the circle with area equal to the sum of two circles of radii 4 cm and 3cm is 10 cm.

Q.8. Find the area of a circle whose circumference is 8π.

Given:
Circumference of circle = 8π
∵ Circumference of a circle = 2πr
∴ 8π = 2πr
r = 4
∵ Area of circle = πr²
∴ Area of circle = π × 4 × 4
= 16π
Hence, the area of the circle is 16π.

Q.9. Find the perimeter of a semicircular protractor whose diameter is 14 cm.

Given:
Diameter of the semicircular protractor = 14 cm
Radius of the protractor = 14/2 cm = 7cm
∵ Perimeter of semicircle = πr + d
∴ Perimeter of semicircular protractor = (22/7)× 7 + 14 = 22 + 14
= 36 cm
Hence, the perimeter of the semicircular protractor is 36 cm.

Q.10. Find the radius of a circle whose perimeter and area are numerically equal.

Given:
Perimeter of circle = Area of circle …… (i)
∵ Perimeter of circle = 2πr and Area of circle = πr²
∴ Using (i), we have
2πr = πr²
2 = πr²/2πr
2 = r or r = 2
Hence, the radius of the circle is 2 cm.

Q.11. The radii of two circles are 19 cm and 9 cm. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.

Given:
Radius of one of the circles, C₁ = 19 cm = r₁
Radius of the other circle, C₂ = 9 cm = r₂
Let the other circle be C with radius ‘r’.
Circumference of C = Circumference of C₁ + Circumference of C₂ …………(i)
∵ Circumference of circle = 2πr
∴ Circumference of C₁ = 2πr₁ = 2 ×  × 19 = 
and Circumference of C₂ = 2πr₂ = 2 ×  × 9 = 
Using (i), we have
2πr =  +  = 
2 ×  × r = 
r =  ×  ×  = 28 
r = 28 cm
Hence, the radius of the circle is 28 cm.

Q.12. The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.

Given:
Radius of one of the circles, C₁ = 8 cm = r₁
Radius of the other circle, C₂ = 6 cm = r₂
Let the other circle be C with radius ‘r’.
Area of C = Area of C₁ + Area of C₂ …… (i)
∵ Area of circle = πr²
∴ Area of C₁ = πr₁² =  × 8 × 8 = 
and Area of C₂ = πr₂² =  × 6 × 6 = 
Using (i), we have
πr² =  +  = 
 × r² = 
r² =  ×  = 100 
r² = 100
r = √100 = 10 or r = 10
Hence, the radius of the circle is 10 cm.

Q.13. Find the area of the sector of a circle having radius 6 cm and of angle 30°.

Given:
Radius of circle = 6 cm
Angle of the sector = 30°
∵ Area of sector =  × πr² 
=  × 3.14 × 6 × 6 
= 3 × 3.14 = 9.42 cm² 
Hence, the area of the sector is 9.42 cm².

Q.14. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc.

Given:
Radius of circle = 21 cm
Angle subtended by the arc = 60°
∵ Length of arc =  × 2πr 
=  × 2 ×  × 21 = 22 cm 
Hence, the length of the arc is 22 cm.

Q.15. The circumferences of two circles are in the ratio 2:3. What is the ratio between their areas?

Given:
Ratio of circumferences of two circles = 2:3
Let the two circles be C1 and C2 with radii ‘r₁’ and ‘r₂’.
∵ Circumference of circle = 2πr
∴ Circumference of C₁ = 2πr₁
and Circumference of C₂ = 2πr₂
⇒  = 
⇒  = 
Squaring both sides, we get
⇒  = 
Multiplying both sides by ‘π’, we get
⇒  = 
∵ Area of circle = πr²
⇒  = 
Hence, the ratio between the areas of C₁ and C₂ is 4:9.

Q.16. The areas of two circles are in the ratio 4:9. What is the ratio between their circumferences?

Given:
Ratio of areas of two circles = 2:3
Let the two circles be C₁ and C₂ with radii ‘r₁’ and ‘r₂’.
∵ Area of circle = πr²
∴ Area of C₁ = πr₁²
and Area of C₂ = πr₂²
⇒  = 
⇒  = 
Taking square root on both sides, we get


Multiplying and dividing L.H.S. by ‘π’, we get

Multiplying and dividing L.H.S. by ‘2’, we get
⇒  = 
As Circumference of circle = 2πr
⇒  = 
Hence, the ratio between the circumferences of C₁ and C₂ is 2:3.

Q.17. A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.

Given:
A square is inscribed in a circle.
Let the radius of circle be ‘r’ and the side of the square be ‘x’.

⇒ The length of the diagonal = 2r
∵ Length of side of square =  
∴ Length of side of square =  = √2r 
Area of square = side × side = x × x = √2r × √2r = 2r²
Area of circle = πr²
Ratio of areas of circle and square = =  = 
Hence, the ratio of areas of circle and square is π:2.

Q.18. The circumference of a circle is 8 cm. Find the area of the sector whose central angle is 72°.

Given:
Circumference of circle = 8 cm
Central angle = 72°
∵ Circumference of a circle = 2πr
∴ 2πr = 8
2 ×  × r = 8 
r = 8 ×  × 
r =  cm 
∵ Area of sector =  × πr² 

= 1.02 cm²

Q.19. A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of the pendulum. 

Given:
Angle made by the pendulum = 30°
Length of the arc made by the pendulum = 8.8 cm
Then the length of the pendulum is equal to the radius of the sector made by the pendulum.
Let the length of the pendulum be ‘r’.
∵ Length of arc =  × 2πr 
∴ We have,
 × 2πr = 8.8 
(30/360) × 2 × 3.14 × r = 8.8 
r = 8.8 × 
r = 16.8 cm
Hence, the length of the pendulum is 16.8 cm.

Q.20. The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.

Given:
Length of minute hand = 15 cm
Here, the length of the minute hand is equal to the radius of the sector formed by the minute hand.
Angle made by the minute hand in 1 minute = 360/60 = 6°
Angle made by the minute hand in 20 minutes = 20 × 6 = 120°
Here, the area swept by the minute hand is equal to the area of the corresponding sector made.
∵ Area of sector = (θ/360) x πr² 
= (120/360) × 3.14 × 15 × 15 = 235.5 cm²
Hence, the area swept by it in 20 minutes is 235.5 cm².

Q.21. A sector of 56°, cut out from a circle, contains 17.6 cm². Find the radius of the circle.

Given:
Angle of the sector = 56°
Area of the sector = 17.6 cm²
Let the radius of the circle be ‘r’.
∵ Area of sector =  × πr² 
∴ 17.6 =  ×  × r² 
r² =  ×  × 17.6 
r² = 36
r = √36
r = 6 cm
Hence, the radius of the circle is 6 cm.

Q.22. The area of the sector of a circle of radius 10.5 cm is 69.3 cm². Find the central angle of the sector.

Given:
Radius of the circle = 10.5 cm
Area of the sector = 69.3 cm²
∵ Area of the sector =  × πr² 
∴ 69.3 =  ×  × 10.5 × 10.5 
θ = 69.3 × 360 ×  ×  × 
θ = 72°
Hence, the central angle is 72°.

Q.23. The perimeter of a certain sector of a circle of radius 6.5 cm is 31 cm. Find the area of sector.

Given:
Radius of circle = 6.5 cm
Perimeter of sector = 31 cm
Now, Perimeter of sector = 2 × radius + Length of arc
∵ Length of arc =  × 2r × 2πr 
∴ Perimeter of sector = 2 × r +  × 2r × π 
= 2r × [1 +  × π] 
31 = 2 × 6.5 × [1 +  × ] 
31 = 13 × [1 +  × ] 
 = 1 +  × 
 - 1 =  × 
 =  × 
θ =  × 360 ×   …. (i) 
∵ Area of sector =  × πr² 
∴ using (i), we have
Area =  × 360 ×  ×  ×  × 6.5 × 6.5
= 18 × 3.25 = 58.5 cm²
Hence, the area of the sector is 58.5 cm². 

Q.24. The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.

Given:
Radius of circle = 17.5 cm
Length of arc = 44 cm
∵ Length of arc =  × 2πr 
∴ 44 =  × 2 ×  × 17.5 
θ = 44 × 360 ×  ×  × 
θ =  = 144° 
Now, Area of sector =  × πr² 
=  ×  × 17.5 × 17.5 = 385 cm² 
Hence, the area of the sector is 385 cm².

Q.25. Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular cardboard of dimensions 14 cm × 7 cm. Find the area of the remaining cardboard.

Given:
Length of the rectangular cardboard = 14 cm
Breadth of the rectangular cardboard = 7 cm

∵ Area of rectangle = length × breadth
∴ Area of cardboard = 14 × 7 = 98 cm²
Let the two circles with equal radii and maximum area have a radius of ‘r’ cm each.
Then, 2r = 7
r = 7/2 cm
∵ Area of circle = πr²
∴ Area of two circular cut outs = 2 × πr²
= 2 ×  ×  × 
= 11 × 7 = 77 cm²
Thus, the area of remaining cardboard = 98 – 77 = 21 cm²
Hence, the area of remaining cardboard is 21 cm².

Q.26. In the given figure, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is also drawn. Find the area of the shaded region.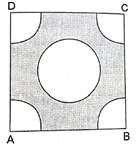

Given:
Side of the square = 4 cm
Radius of the quadrants at the corners = 1 cm
Radius of the circle in the centre = 1 cm
∵ 4 quadrants = 1 circle
∴ There are 2 circles of radius 1 cm
Area of square = side × side
= 4 × 4 = 16 cm²
Area of 2 circles = 2 × πr2
= 2 ×  × 1 × 1 =  cm² 
∵ Area of shaded region = Area of square – Area of 2 circles
= 16 - (44/7)
=  =  cm² = 9.7 cm² 
Hence, the area of shaded region is 9.72 cm².

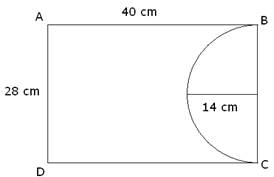
Q.27. From a rectangular sheet of paper ABCD wit AB = cm and AD = 28 cm, a semicircular portion wit BC as diameter is cut off. Find the area of the remaining paper.

Given:
Length of rectangular sheet of paper = 40 cm
Breadth of rectangular sheet of paper = 28 cm
Radius of the semicircular cut out = 14 cm

∵ Area of rectangle = length × breadth
∴ Area of rectangular sheet of paper = 40 × 28
= 1120 cm²
∵ Area of semicircle = (1/2)πr²
∴ Area of semicircular cut out =  ×  × 14 × 14 
= 22 × 14 = 308 cm²
Thus, the area of remaining sheet of paper = Area of rectangular sheet of paper – Area of semicircular cut out
= 1120 – 308 = 812 cm²
Hence, the area of remaining sheet of paper is 812 cm².

Q.28. In the given figure, OABC is a square of side 7 cm. If COPB is a quadrant of a circle wit centre C find the area of the shaded region.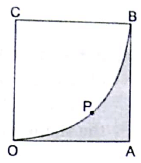

Given:
Side of square = 7 cm
Radius of the quadrant = 7 cm
Area of square = side × side
= 7 × 7 = 49 cm²
∵ Area of circle = πr²
∴ Area of a quadrant = (1/4) πr²
=  ×  × 7 × 7 
= 77/2 = 38.5 cm²
Thus, the area of shaded region = Area of square – Area of quadrant
= 49 – 38.5 = 10.5 cm²
Hence, the area of the shaded region is 10.5 cm².

Q.29. In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.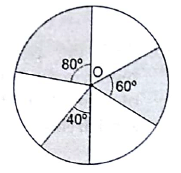

Given:
Radius of circle = 7 cm
Let the sectors with central angles 80°, 60° and 40° be S₁, S₂, and S₃ respectively.
Then, the area of shaded region = Area of S₁ + Area of S₂ + Area of S₃  ... (i)
∵ Area of sector = (θ/360) × πr²
∴ Area of S₁ =  ×  × 7 × 7 
= (308/9) cm² 
Similarly, Area of S₂ =  ×  × 7 × 7 
= 154/6 cm²
and Area of S₃ =  ×  × 7 × 7 
= 154/9 cm²
Thus, using (i), we have
Area of shaded region =  +  + 
= 
= 1386/18 = 77cm²
Hence, the area of shaded region is 77 cm².

Q.30. In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.

Given:
Radius of inner circle = 3.5 cm
Radius of outer circle = 7 cm
∠POQ = 30°
Let the sector made by the arcs PQ and AB be S₁ and S₂ respectively.
Then, Area of shaded region = Area of S₁ – Area of S₂ ….(i)
∵ Area of sector = (θ/360) x πr² 
∴ Area of S₁ =  ×  × 7 × 7 
= 71/6 cm²
Similarly, Area of S₂ =  ×  × 3.5 × 3.5 
= 77/24 cm²
Thus, using (i), we have
Area of shaded region =  - 
= 
=  =  cm² 
Hence, the area of shaded region is 77/8 cm².

Q.31. In the given figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircle.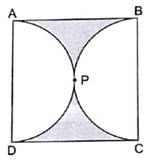

Given:
Side of square = 14 cm
Diameter of each semicircle = 14 cm
Radius of each semicircle = 14/2 = 7 cm
∵ Both the semicircles have same radius.
∴ We consider one circle of radius 7 cm.
Area of shaded region = Area of square – Area of circle  …. (i)
Area of square = side × side
= 14 × 14 = 196 cm²
Area of circle = πr²
= 22/7 × 7 × 7 = 22 × 7 = 154 cm²
Thus, using (i), we have
Area of shaded region = 196 – 154 = 42 cm²
Hence, the area of shaded region is 42 cm².

Q.32. In the given figure, the shape of the top of a table is that of a sector of circle with centre O and ∠AOB = 90°. If AO = OB = 42 cm, then find the perimeter of the top of the table.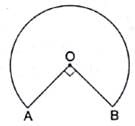

Give:
Radius of the circle = 42 cm
Central angle of the sector = ∠AOB = 90°
Perimeter of the top of the table = Length of the major arc AB + 2 × radius ……. (i)
Length of major arc AB =  × 2πr 
=  × 2 ×  × 42 
= (270/360) × 2 × 22 × 6
= 3/4 × 264 = 3 × 66 = 198 cm
Thus, using (i), we have
Perimeter of the top of the table = 198 + 2 × 42
= 198 + 84 = 282 cm
Hence, the perimeter of the top of the table is 282 cm.

Q.33. In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.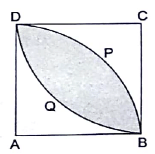

Given:
Side of square = 7 cm
Radius of each quadrant = 7 cm
Area of square = side × side = 7 × 7 = 49 cm²
∵ Area of quadrant = 1/4 πr²
∴ Area of 2 quadrants = 2 × 1/4 × πr²
=  ×  × 7 × 7 
= 77 cm²
Area of shaded region = Area of 2 quadrants – Area of square
= 77 – 49 = 28 cm²
Hence, the area of shaded region is 28 cm².

Q.34. In the given figure, OABC is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.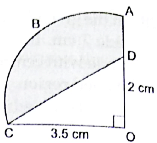

Given:
Radius of Circle = 3.5 cm
OD = 2 cm
∵ Area of Quadrant = 1/4 πr²
∴ Area of Quadrant OABC =  1/4 × 22/7 × 3.5 × 3.5
= 9.625 cm²
∵ Area of Triangle = 1/2 × Base × Height
∴ Area of Δ COD = 1/2 × 3.5 × 2 
= 3.5 cm²
Area of Shaded Region = Area of Quadrant OABC – Area of  ΔCOD
= 38.5 – 3.5 = 35 cm²
Hence, the area of shaded region is 35 cm².

Q.35. Find the perimeter of shaded region in the figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles.

Given:
Side of square = 14 cm
Diameter of semi circle = 14 cm
⇒ Radius of semi circle = 14/2 = 7 cm
∵ There are 2 semi circles of same radius.
∴ We consider it as one circle with radius 7 cm.
So,
Perimeter of 2 semicircles = Perimeter of circle = 2πr
= 2 × (22/7) × 7 
= 2 × 22 = 44 cm
Perimeter of shaded region = Perimeter of 2 semicircles + 2 × Side of Square = 44 + 2 × 14 = 44 + 28 = 72 cm
Hence, the area of the shaded region is 72 cm.

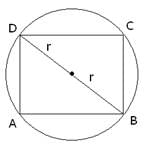
Q.36. In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.

Given:
Radius of the circle = 7 cm
Diameter of the circle = 14 cm
Here, diagonal of square = 14 cm
∵ Side of a square =
⇒ Side = 14/√2 = 7√2 cm 
⇒ Area of square = side × side
= 7√2 × 7√2
= 49 × 2 = 98 cm²
Area of circle = πr²
= 22/7 × 7 × 7 = 22 × 7 = 154 cm² 
Thus, the area of the circle outside the square
= Area of circle – Area of square = 154 – 98 = 56 cm²
Hence, the area of the required region is 56 cm².

Q.37. In the given figure, APB and CQD are semicircle of diameter 7 cm each, while ARC and BSD are semicircles of diameter 14 cm each. Find the (i) perimeter, (ii) area of the shaded region.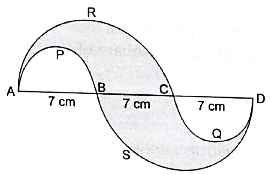

(i) Given:
Diameter of semicircles APB and CQD = 7 cm
⇒ Radius of semicircles APB and CQD = 7/2cm = r₁
Diameter of semicircles ARC and BSD = 14 cm
⇒ Radius of semicircles ARC and BSD = 14/2 cm = 7 cm = r₂
Perimeter of APB = Perimeter of CQD
Area of APB = Area of CQD ………….. (i)
Perimeter of ARC = Perimeter of BSD
Area of ARC = Area of BSD ………….. (ii)
∵ Perimeter of semicircle = πr …………… (iii)
∴ Perimeter of APB = πr₁
=  ×  = 11 cm 
Then, using (i), we have
Perimeter of CQD = 11 cm
Now, using (iii), we have
Perimeter of ARC = πr₂
= (22/7) × 7 = 22 cm 
Then, using (ii), we have
Perimeter of BSD = 22 cm
Perimeter of shaded region
= (Perimeter of ARC + Perimeter of APB) + (Perimeter of BSD + Perimeter of CQD)
= (22 + 11) + (22 + 11) = 33 + 33 = 66 cm
Hence, the perimeter of the shaded region is 66 cm.
(ii) Now,
∵ Area of semicircle = (1/2) πr²  …. (iv)
∴ Area of APB = (1/2) πr₁²
=  ×  ×  ×  =  cm² 
Then, using (i), we have
Area of CQD = 77/4 cm²
Now, using (iv), we have
Area of ARC = 1/2 πr₂² 
=  ×  × 7 × 7 = 11 × 7 = 77 cm² 
Then, by using (ii), we have
Area of BSD = 77 cm²
Area of shaded region
= (Area of ARC-Area of APB) + (Area of BSD- Area of CQD) 
= (77 - ) + (77 - ) 
= () + () =  +  =  = 115.5 cm² 
Hence, the area of the shaded region is 115.5 cm².

Q.38. In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.

Given:
Diameter of semicircle PSR = 10 cm
⇒ Radius of semicircle PSR = 10/2 = 5 cm = r₁
Diameter of semicircle RTQ = 3 cm
⇒ Radius of semicircle RTQ = 3/2 = 1.5 cm = r₂
Diameter of semicircle PAQ = 7 cm
⇒ Radius of semicircle PAQ = 7/2 = 3.5 cm = r₃
∵ Perimeter of semicircle = πr
∴ Perimeter of semicircle PSR = πr₁
= 3.14 × 5 = 15.7 cm
Similarly, Perimeter of semicircle RTQ = πr₂
= 3.14 × 1.5 = 4.71 cm
and Perimeter of semicircle PAQ = πr₃
= 3.14 × 3.5 = 10.99 cm
Perimeter of shaded region = Perimeter of semicircle PSR
+ Perimeter of semicircle RTQ
+ Perimeter of semicircle PAQ
= 15.7 + 4.71 + 10.99 = 31.4 cm
Hence, the perimeter of the shaded region is 31.4 cm.

Q.39. In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. IF OA = 20 cm, find the area of the shaded region. [Use π = 3.14]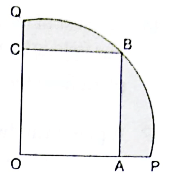

Given:
OA = Side of square OABC = 20 cm
∵ Area of square = Side × Side
∴ Area of square OABC = 20 × 20 = 400 cm2
Now,
∵ Length of diagonal of square = √2 × Side of Square
∴ Length of diagonal of square OABC = √2 × 20 = 20√2 cm
⇒ Radius of the quadrant = 20√2 cm
∵ Area of quadrant = 1/4πr²
∴ Area of quadrant OPBQ = (1/4) × 3.14 × 20√2 × 20√2 
= 3.14/4 × 400 × 2
= 3.14 × 200 = 628 cm²
Area of shaded region = Area of quadrant OPBQ – Area of square OABC = 628 – 400 = 228 cm²
Hence, the area of the shaded region is 228 cm².

Q.40. In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.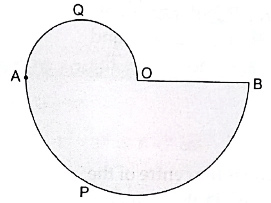

Given:
AO = OB
Perimeter of the figure = 40 cm………….. (i)
Let the diameters of semicircles AQO and APB be ‘x₁’ and ‘x₂’ respectively.
Then, using (1), we have
AO = OB
Also, AB = AO + OB = AO + AO = 2AO
⇒ x₂ = 2x₁
So, diameter of APB = 2x₁
and diameter of AQO = x₁
Radius of APB = x₁
and Radius of AQO =x₁/2   ….. (ii)
Perimeter of shaded region = perimeter of AQO + perimeter APB + diameter of APB  …… (iii)
∵ Perimeter of semicircle = πr
∴ Perimeter of semicircle AQO =   ×  =  cm 
Perimeter of semicircle APB =  × x₁ =  cm 
Now, using (iii), we have


40 × 7 = 40x₁
280 = 40x₁
x₁ = 280/40 = 7 cm 

∴ using (ii), we have
Radius of APB = 7 cm = r₁
And Radius of AQO = 7/2 cm = 3.5 cm = r₂
Now,
∵ Area of semicircle = 1/2 πr²
∴ Area of semicircle APB = 1/2 πr₁²

Similarly,
Area of semicircle APB = 1/2 πr₂²

Thus, Area of shaded region = Area of APB + Area of AQO
= 77 + 19.25 = 96.25 cm²
Hence, the area of the shaded region is 96.25 cm².

Q.41. Find the area of a quadrant of a circle whose circumference is 44 cm.

Given:
Circumference of circle = 44 cm
Let the radius of the circle be ‘r’ cm
∵ Circumference of circle = 2πr
∴ 44 = 2πr
 =  × r 
r = 22 × (7/22) = 7 cm 
Now, Area of quadrant = 1/4 × πr²


Hence, the area of the quadrant is 38.5 cm².

Q.42. In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.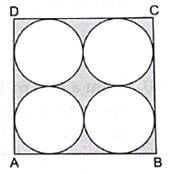

Given:
Side of square = 14 cm
Let the radius of each circle be ‘r’ cm
Then, 2r + 2r = 14 cm
4r = 14 cm
r = 14/4
= 7/2
Area of square = side × side
= 14 × 14
= 196 cm²
∵ Area of circle = πr²
∴ Area of 4 circles = 4 × πr²

= 22 × 7= 154 cm²
Area of shaded region = Area of the square – Area of 4 circles
= 196 -154
= 42 cm²
Hence, the area of the shaded region is 42 cm².

Q.43. Find the area of the shaded region in the given figure, if ABCD is a rectangle wit sides 8 cm and 6 cm ad O is the centre of the circle.

Given:
Length of rectangle = 8 cm
Breadth of rectangle = 6 cm
Area of rectangle = length × breadth
= 8 × 6 = 48 cm²
Consider Δ ABC,
By Pythagoras theorem,
AC² = AB² + BC²
= 8² + 6² = 64 + 36 = 100
AC = √100 = 10 cm
⇒ Diameter of circle = 10 cm
Thus, radius of circle = 10/2 = 5 cm
Let the radius of circle be r = 5 cm
Then, Area of circle = πr²
=  × 5 × 5 =  =  = 78.57 cm² 
Area of shaded region = Area of circle – Area of rectangle
= 78.57 - 48
= 30.57 cm²
Hence, the area of shaded region is 30.57 cm².

Q.44. A wire is bent to form a square enclosing an area of 484 m². Using the same wire, a circle is formed. Find the area of the circle.

Given:
Perimeter of square = Circumference of circle ……. (i)
Area of Square = 484m²
Let the side of square be ‘x’ cm.
∵ Area of Square = side × side
∴ 484 = x × x
x² = 484
x = √484 = 22cm
∵ Perimeter of square = 4 × side
= 4 × 22 = 88 cm
∴ Using (i), we have
Circumference of circle = 88 cm
Also, Circumference of Circle = 2πr
2πr = 88
2 × 22/7 × r = 88

r = 2 × 7 = 14 cm
Area of Circle = πr² = 22/7 × 14 × 14
= 22 × 2 × 14 = 616 cm²
Hence, the area of Circle is 616 cm².

Q.45. A square ABCD is inscribed in a circle of radius ‘r’. Find the area of the square.

Given: Radius of circle = r

Diagonal of Square = 2r
∵ Side of Square =
∴ Side =  = √2r 
Area of Square = Side × Side
= √2r × √2r
= 2r²
Hence, the area of square is ‘2r²’ square units.

Q.46. The cost of fencing a circular field at the rate of Rs. 25 per meter is Rs. 5500. The field is to be ploughed at the rate of 50 paise per m². Find the cost of ploughing the field. [Take π = 22/7]

Given:
Rate of fencing a circular field = Rs. 25/m
Cost of fencing a circular field = Rs. 5500
Rate of ploughing the field = 50p/m2 = Rs. 0.5/m²
Let the radius of circular field be ‘r’ and the length of the field fenced be ‘x’ m.
Then, 25 × x = 5500
x = 5500/25 = 220 m
∵ Circumference of circular field = 2πr
∴ 220 = 2πr
220 = 2 × 22/7 × r
r = 
r = 35 m
Area of the circular field = πr²
= 22/7 × 35 × 35
= 22 × 5 × 35
= 3850m²
Now, cost of ploughing the field = Rate of ploughing the field × Area of the field = 0.5 × 3850
= Rs. 1925
Hence, the cost of Ploughing the field is Rs. 1925.

Q.47. A park is in the form of a rectangle 120 m by 90 m. At the centre of the park, there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn. [Given, π = 3.14]

Given:
Length of the rectangular park = 120 m
Breadth of the rectangular park = 90 m
Area of the park excluding the circular lawn = 2950m²
Area of the rectangular park = length × breadth
= 120 × 90 = 10800m²
Area of circular lawn = Area of rectangular park – Area of park excluding the lawn
= 10800 – 2950
= 7850m²
∵ Area of circle = πr²
∴ 7850 = 3.14 × r²
r² = 7850/3.14 = 2500
r = √2500 = 50 m
Hence, the radius of the circular lawn is 50m.

Q.48. In the given figure PQSR represents a flower be. If OP = 21 m and OR = 14 m, find the area of the flower bed.

Given:
OP = 21 m = r₁
OR = 14 m = r₂
Let the quadrants made by outer and inner circles be Q₁ and Q₂, with radius r₁ and r₂ respectively.
Then, Area of flower bed = Area of Q₁ – Area of Q₂
∵ Area of Quadrant = 1/4 πr²
∴ Area of Q1 = 1/4 πr₁²
= 1/4 × 22/7 × 21 × 21= 693/2 m²
Similarly, Area of Q₂ = 1/4 πr₂²
= 1/4 × 22/7 × 14 × 14
= 308/2 m²
Thus, Area of flower bed = 693/2 - 308/2
= 385/2 = 192.5 m²
Hence, the area of the flower bed is 192.5 m².

Q.49. In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm, find the area of the shaded region.

Given:
AC = 54 cm
BC = 10 cm
⇒ AB = AC-BC = 54-10 = 44 cm
Radius of bigger circle = AC/2 = 54/2 = 27 cm = r₁
Radius of Smaller circle = AB/2 = 44/2 = 22 cm = r₂
∵ Area of Circle = πr²
∴ Area of Bigger Circle = πr₁²
= (22/7) × 27 × 27
= 16038/7 cm²
Similarly, Area of Smaller Circle = πr₂²
= (22/7) × 22 × 22
= 10648/7 cm²
Area of shaded region = Area of Bigger Circle – Area of Smaller Circle = 16038/7 - 10648/7 = 5390/7 = 770 cm²
Hence, Area of Shaded Region is 770 cm².

Q.50. From a thin metallic piece in the shape of a trapezium ABCD in which AB ∥ CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.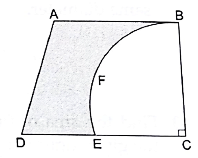

Given:
AB ∥ CD
∠BCD = 90°
AB = BC = 3.5 cm = EC
DE = 2 cm
DC = DE + EC = 2 + 3.5 = 5.5 cm
Area of Trapezium = 1/2 × Sum of Parallel Sides × h
= 1/2 × (AB + DC) × BC
= 1/2 × (3.5 + 5.5) × 3.5
= 1/2 × 9 × 3.5
= 15.75 cm²
Area of Quadrant BFEC = 1/4 × πr² = 1/4 × 22/7 × 3.5 × 3.5
= 9.625 cm²
Thus, Area of remaining part of metal sheet
= Area of Trapezium – Area of Quadrant BFEC
= 15.75 – 9.625 = 6.125 cm²
Hence, the area of the remaining part of metal sheet is 6.125 cm².

Q.51. Find the area of the major segment APB of a circle of radius 35 cm and ∠AOB = 90°, as shown in the given figure.

Given:
Radius of Circle = 35 cm
∠AOB = 90°
∵ Area of Sector =  × πr² 
=  ×  × 35 × 35 
= 1925/2 cm² 
∵ ∆ AOB is right-angled triangle.
∴ Area of ∆ AOB = 1/2 × OA × OB
= 1/2 × 35 × 35
= 1225/2 cm²
Now, Area of Minor Segment ACB
= Area of Sector – Area of ∆AOB
= 1925/2 - 1225/2 = 700/2 = 350 cm²
Area of Circle = πr²
= 22/7 × 35 × 35
= 22 × 5 × 35
= 3850 cm²
Thus, Area of Major Segment = Area of Circle – Area of Minor Segment = 3850 – 350 = 3500 cm²
Hence, the area of the major segment is 3500 cm².