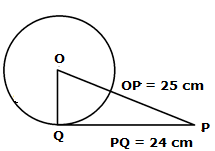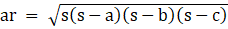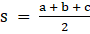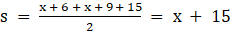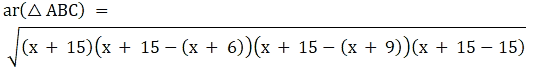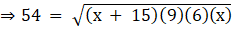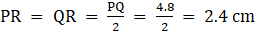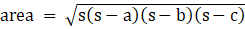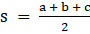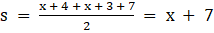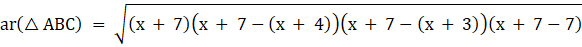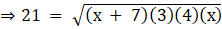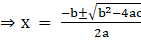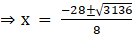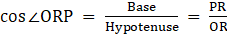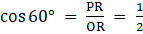RS Aggarwal Solutions: Circles- 1 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
Exercise: 12a
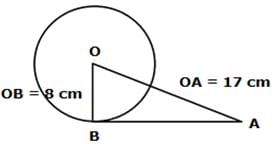
Q.1. Find the length of tangent drawn to a circle with radius 8 cm from a point 17 cm away from the center of the circle.
Let us consider a circle with center O and radius 8 cm.
The diagram is given as:Consider a point A 17 cm away from the center such that OA = 17 cm
A tangent is drawn at point A on the circle from point B such that OB = radius = 8 cm
To Find: Length of tangent AB = ?
As seen OB ⏊ AB
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
∴ In right - angled ΔAOB, By Pythagoras Theorem
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2 ]
(OA)2 = (OB)2 + (AB)2
(17)2 = (8)2 + (AB)2
289 = 64 + (AB)2
(AB)2 = 225
AB = 15 cm
∴ The length of the tangent is 15 cm.
Q.2. A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
Let us consider a circle with center O.
Consider a point P 25 cm away from the center such that OP = 25 cm
A tangent PQ is drawn at point Q on the circle from point P such that PQ = 24 cm
To Find : Length of radius OQ = ?
Now, OQ ⏊ PQ
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
∴ In right - angled △POQ,
By Pythagoras Theorem,
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2 ]
(OP)2 = (OQ)2 + (PQ)2
(25)2 = (OQ)2 + (24)2
625 = (OQ)2 + 576
(OQ)2 = 49
OQ = 7 cm
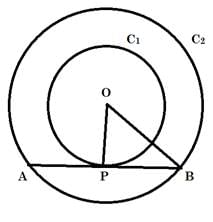
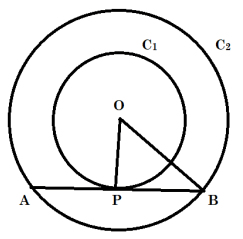
Q.3. Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Given: Two concentric circles (say C1 and C2) with common center as O and radius r1 = 6.5 cm and r2 = 2.5 cm respectively.
To Find: Length of the chord of the larger circle which touches the circle C2. i.e. Length of AB.
As AB is tangent to circle C2 and we know that "Tangent at any point on the circle is perpendicular to the radius through point of contact"
So, we have,
OP ⏊ AB
∴ OPB is a right - angled triangle at P,
By Pythagoras Theorem in △OPB
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2 ]
We have,
(OP)2 + (PB)2 = (OB)2
r22 + (PB)2 = r12
(2.5)2 + (PB)2= (6.5)2
6.25 + (PB)2 = 42.25
(PB)2 = 36
PB = 6 cm
Now, AP = PB ,
[ as perpendicular from center to chord bisects the chord and OP ⏊ AB ]
So,
AB = AP + PB = PB + PB
= 2PB = 2(6)
= 12 cm
Q.4. In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.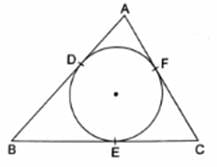
Let AD = x cm, BE = y cm and CF = z cm
As we know that,
Tangents from an external point to a circle are equal,
In given Figure we have
AD = AF = x [Tangents from point A]
BD = BE = y [Tangents from point B]
CF = CE = z [Tangents from point C]
Now, Given: AB = 12 cm
AD + BD = 12
x + y = 12
y = 12 – x…. [1]
and BC = 8 cm
BE + EC = 8
y + z = 8
12 - x + z = 8 [From 1]
z = x – 4…. [2]
and
AC = 10 cm
AF + CF = 10
x + z = 10 [From 2]
x + x - 4 = 10
2x = 14
x = 7 cm
Putting value of x in [1] and [2]
y = 12 - 7 = 5 cm
z = 7 - 4 = 3 cm
So, we have AD = 7 cm, BE = 5 cm and CF = 3 cm
Q.5. In the given figure, PA and PB are the tangent segments to a circle with center 0. Show that the points A, O, B and P are concyclic.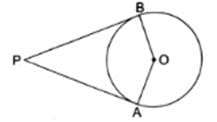
Given: PA and PB are tangents to a circle with center O
To show : A, O, B and P are concyclic i.e. they lie on a circle i.e. AOBP is a cyclic quadrilateral.
Proof:
OB ⏊ PB and OA ⏊ AP
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
∠OBP = ∠OAP = 90°
∠OBP + ∠OAP = 90 + 90 = 180°
AOBP is a cyclic quadrilateral i.e. A, O, B and P are concyclic.
[ As we know if the sum of opposite angles in a quadrilateral is 180° then quadrilateral is cyclic]
Hence Proved.
Q.6. In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.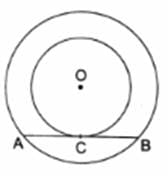
Given: Two concentric circles with common center as O
To Prove: AC = CB
Construction: Join OC, OA and OB
Proof :
OC ⏊ AB
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
In △OAC and △OCB, we have
OA = OB
[∵ radii of same circle]
OC = OC
[∵ common]
∠OCA = ∠OCB
[∵ Both 90° as OC ⏊ AB]
△OAC ≅ △OCB
[By Right Angle - Hypotenuse - Side]
AC = CB
[Corresponding parts of congruent triangles are congruent]
Hence Proved.
Q.7. From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14 cm, find the perimeter of △PCD.
Given : From an external point P, two tangents, PA and PB are drawn to a circle with center O. At a point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. And PA = 14 cm
To Find : Perimeter of △PCD
As we know that, Tangents drawn from an external point to a circle are equal.
So we have
AC = CE …[1] [Tangents from point C]
ED = DB …[2] [Tangents from point D]
Now Perimeter of Triangle PCD
= PC + CD + DP
= PC + CE + ED + DP
= PC + AC + DB + DP [From 1 and 2]
= PA + PB
Now,
PA = PB = 14 cm as tangents drawn from an external point to a circle are equal
So we have
Perimeter = PA + PB = 14 + 14 = 28 cm
Q.8. A circle is inscribed in a LABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR = 7 cm and CR = 5 cm, find the length of BC.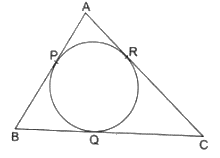
As we know that tangents drawn from an external point to a circle are equal ,
In the Given image we have,
AP = AR = 7 cm ….[1]
[tangents from point A]
CR = QC = 5 cm ….[2]
[tangents from point C]
BQ = PB …[3]
[tangents from point B]
Now,
AB = 10 cm [Given]
AP + PB = 10 cm
7 + PB = 10 [From 1]
PB = 3 cm
BQ = 3 cm …..[4]
[From 3]
BC = BQ + QC = 5 + 3 = 8 cm [ From 2 and 4]
Q.9. In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6 cm, BC = 7 cm and CD = 4 cm. Find AD.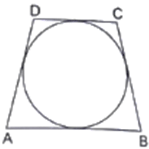
Let sides AB, BC, CD, and AD touches circle at P, Q, R and S respectively.
As we know that tangents drawn from an external point to a circle are equal,
In the given image we have,
AP = AS = w (say) [Tangents from point A]
BP = BQ = x (say) [Tangents from point B]
CP = CR = y (say) [Tangents from point C]
DR = DS = z (say) [Tangents from point D]
Now,
Given,
AB = 6 cm
AP + BP = 6
w + x = 6 …[1]
BC = 7 cm
BP + CP = 7
x + y = 7 ….[2]
CD = 4 cm
CR + DR = 4
y + z = 4 ….[3]
Also,
AD = AS + DS = w + z ….[4]
Add [1] and [3] and substracting [2] from the sum we get,
w + x + y + z - (x + y) = 6 + 4 - 7
w + z = 3 cm ; From [4]
AD = 3 cm
Q.10. In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.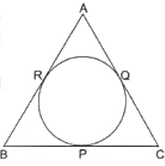
As we know that tangents drawn from an external point to a circle are equal,
BR = BP [ Tangents from point B] [1]
QC = CP [ Tangents from point C] [2]
AR = AQ [ Tangents from point A] [3]
As ABC is an isosceles triangle,
AB = BC [Given] [4]
Now substract [3] from [4]
AB - AR = BC - AQ
BR = QC
BP = CP [ From 1 and 2]
∴ P bisects BC
Hence Proved.
Q.11. In the given figure, O is the center of two concentric circles of radii 4 cm and 6 cm respectively. PA and PB are tangents to the outer and inner circle respectively. If PA = 10 cm, find the length of PB up to one place of decimal.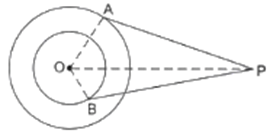
In given Figure,
OA ⏊ AP
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
∴ In right - angled △OAP,
By Pythagoras Theorem
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2]
(OP)2 = (OA)2 + (PA)2
Given, PA = 10 cm and OA = radius of outer circle = 6 cm
(OP)2 = (6)2 + (100)2
(OP)2 = 36 + 100 = 136 [1]
Also,
OB ⏊ BP
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
∴ In right - angled △OBP,
By Pythagoras Theorem
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2]
(OP)2 = (OB)2 + (PB)2
Now, OB = radius of inner circle = 4 cm
And from [2]
(OP)2 = 136
136 = (4)2 + (PB)2
(PB)2 = 136 - 16 = 120
PB = 10.9 cm
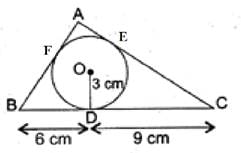
Q.12. In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 6 cm and 9 cm respectively. If the area of ABC = 54 cm2 then find the lengths of sides AB and AC.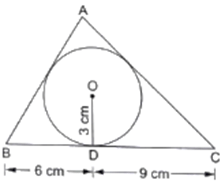
Given : △ABC that is drawn to circumscribe a circle with radius r = 3 cm and BD = 6 cm DC = 9cm
Also, area(△ABC) = 54 cm2
To Find : AB and AC
Now,
As we know tangents drawn from an external point to a circle are equal.
Then,
FB = BD = 6 cm [Tangents from same external point B]
DC = EC = 9 cm [Tangents from same external point C]
AF = EA = x (let) [Tangents from same external point A]
Using the above data, we get
AB = AF + FB = x + 6 cm
AC = AE + EC = x + 9 cm
BC = BD + DC = 6 + 9 = 15 cm
Now we have heron's formula for area of triangles if its three sides a, b and c are given
Where,
⇒
So for △ABC
a = AB = x + 6
b = AC = x + 9
c = BC = 15 cm
⇒
And
Squaring both sides, we get,
54(54) = 54x(x + 15)
x2 + 15x - 54 = 0
x2 + 18x - 3x - 54 = 0
x(x + 18) - 3(x + 18) = 0
(x - 3)(x + 18) = 0
x = 3 or - 18
but x = - 18 is not possible as length can't be negative.
So
AB = x + 6 = 3 + 6 = 9 cm
AC = x + 9 = 3 + 9 = 12 cm
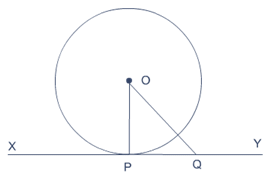
Q.13. PQ is a chord of length 4.8 cm of a circle of radius 3 cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.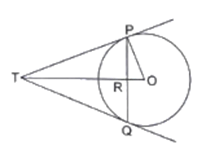
Given : A circle with center O and radius 3 cm and PQ is a chord of length 4.8 cm. The tangents at P and Q intersect at point T
To Find : Length of TP
Construction : Join OQ
Now in △OPT and △OQT
OP = OQ [radii of same circle]
PT = PQ
[tangents drawn from an external point to a circle are equal]
OT = OT [Common]
△OPT ≅ △OQT [By Side - Side - Side Criterion]
∠POT = ∠OQT
[Corresponding parts of congruent triangles are congruent]
or ∠POR = ∠OQR
Now in △OPR and △OQR
OP = OQ [radii of same circle]
OR = OR [Common]
∠POR = ∠OQR [Proved Above]
△OPR ≅ △OQT [By Side - Angle - Side Criterion]
∠ORP = ∠ORQ
[Corresponding parts of congruent triangles are congruent]
Now,
∠ORP + ∠ORQ = 180° [Linear Pair]
∠ORP + ∠ORP = 180°
∠ORP = 90°
⇒ OR ⏊ PQ
⇒ RT ⏊ PQ
As OR ⏊ PQ and Perpendicular from center to a chord bisects the chord we have
∴ In right - angled △OPR,
By Pythagoras Theorem
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2]
(OP)2 = (OR)2 + (PR)2
(3)2 = (OR)2 + (2.4)2
9 = (OR)2 + 5.76
(OR)2= 3.24
OR = 1.8 cm
Now,
In right angled △TPR,
By Pythagoras Theorem
(PT)2 = (PR)2 + (TR)2 …[1]
Also, OP ⏊ OT
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
In right angled △OPT, By Pythagoras Theorem
(PT)2 + (OP)2 = (OT)2
(PR)2 + (TR)2 + (OP)2= (TR + OR)2 …[From 1]
(2.4)2 + (TR)2 + (3)2 = (TR + 1.8)2
4.76 + (TR)2 + 9 = (TR)2 + 2(1.8)TR + (1.8)2
13.76 = 3.6TR + 3.24
3.6TR = 10.52
TR = 2.9 cm [Appx]
Using this in [1]
PT2 = (2.4)2 + (2.9)2
PT2 = 4.76 + 8.41
PT2 = 13.17
PT = 3.63 cm [Appx]
Q.14. Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its center.
Given: A circle with center O and AB and CD are two parallel tangents at points P and Q on the circle.
To Prove: PQ passes through O
Construction: Draw a line EF parallel to AB and CD and passing through O
Proof :
∠OPB = 90°
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
Now, AB || EF
∠OPB + ∠POF = 180°
90° + ∠POF = 180°
∠POF = 90° …[1]
Also,
∠OQD = 90°
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
Now, CD || EF
∠OQD + ∠QOF = 180°
90° + ∠QOF = 180°
∠QOF = 90° [2]
Now From [1] and [2]
∠POF + ∠QOF = 90 + 90 = 180°
So, By converse of linear pair POQ is a straight Line
i.e. O lies on PQ
Hence Proved.
Q.15. In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29 cm, AD = 23 cm, LB = 90° and DS = 5 cm then find the radius of the circle.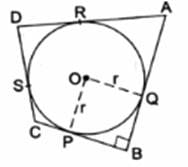
In quadrilateral POQB
∠OPB = 90°
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
∠OQB = 90°
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
∠PQB = 90° [Given]
By angle sum property of quadrilateral PQOB
∠OPB + ∠OQB + ∠PBQ + ∠POQ = 360°
90° + 90° + 90° + ∠POQ = 360°
∠POQ = 90°
As all angles of this quadrilaterals are 90° The quadrilateral is a rectangle
Also, OP = OQ = r
i.e. adjacent sides are equal, and we know that a rectangle with adjacent sides equal is a square
∴ POQB is a square
And OP = PB = BQ = OQ = r [1]
Now,
As we know that tangents drawn from an external point to a circle are equal
In given figure, We have
DS = DR = 5 cm
[Tangents from point D and DS = 5 cm is given]
AD = 23 cm [Given]
AR + DR = 23
AR + 5 = 23
AR = 18 cm
Now,
AR = AQ = 18 cm
[Tangents from point A]
AB = 29 cm [Given]
AQ + QB = 29
18 + QB = 29
QB = 11 cm
From [1]
QB = r = 11 cm
Hence Radius of circle is 11 cm.
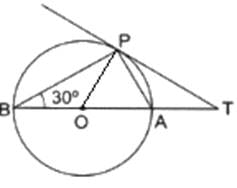
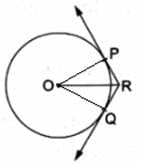
Q.16. In the given figure, O is the center of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30°, prove that BA : AT = 2 : 1.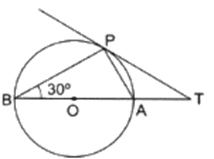
In Given Figure, we have a circle with center O let the radius of circle be r.
Construction : Join OP
Now, In △APB
∠ABP = 30°
∠APB = 90°
[Angle in a semicircle is a right angle]
By angle sum Property of triangle,
∠ABP + ∠APB + ∠PAB = 180
30° + 90° + ∠PAB = 180
∠PAB = 60°
OP = OA = r [radii]
∠PAB = ∠OPA = 60°
[Angles opposite to equal sides are equal]
By angle sum Property of triangle
∠OPA + ∠OAP + ∠AOP = 180°
60° + ∠PAB + ∠AOP = 180
60 + 60 + ∠AOP = 180
∠AOP = 60°
As all angles of △OPA equals to 60°, △OPA is an equilateral triangle
So, we have, OP = OA = PA = r [1]
∠OPT = 90°
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
∠OPA + ∠APT = 90
60 + ∠APT = 90
∠APT = 30°
Also,
∠PAB + ∠PAT = 180° [Linear pair]
60° + ∠PAT = 180°
∠PAT = 120°
In △APT
∠APT + ∠PAT + ∠PTA = 180°
30° + 120° + ∠PTA = 180°
∠PTA = 30°
So,
We have
∠APT = ∠PTA = 30°
AT = PA
[Sides opposite to equal angles are equal]
AT = r [From 1] [2]
Now,
AB = OA + OB = r + r = 2r [3]
From [2] and [3]
AB : AT = 2r : r = 2 : 1
Hence Proved !
Exercise: 12b
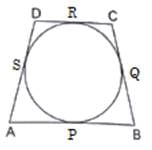
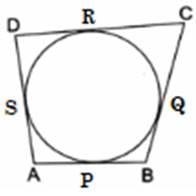
Q.1. In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD.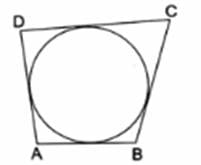
Let sides AB, BC, CD, and AD touches circle at P, Q, R and S respectively.
As we know that tangents drawn from an external point to a circle are equal ,
In the given image we have,
AP = AS = w (say) [Tangents from point A]
BP = BQ = x (say) [Tangents from point B]
CP = CR = y (say) [Tangents from point C]
DR = DS = z (say) [Tangents from point D]
Now,
Given,
AB = 6 cm
AP + BP = 6
w + x = 6 [1]
BC = 9 cm
BP + CP = 9
x + y = 9 [2]
CD = 8 cm
CR + DR = 8
y + z = 8 [3]
Also,
AD = AS + DS = w + z [4]
Add [1] and [3] and substracting [2] from the sum we get,
w + x + y + z - (x + y) = 6 + 8 - 9
w + z = 5 cm
From [4]
AD = 5 cm
Q.2. In the given figure, PA and PB are two tangents to the circle with center O. If ∠APB = 50° then what is the measure of ∠OAB.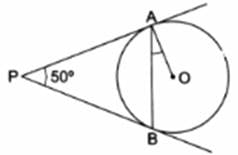
In the given figure, PA and PB are two tangents from common point P
∴ PA = PB
[Tangents drawn from an external point are equal]
∠PBA = ∠PAB
[Angles opposite to equal angles are equal] [1]
By angle sum property of triangle in △APB
∠APB + ∠PBA + ∠PAB = 180°
50° + ∠PAB + ∠PAB = 180° [From 1]
2∠PAB = 130°
∠PAB = 65° [2]
Now,
∠OAP = 90°
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
∠OAB + ∠PAB = 90°
∠OAB + 65° = 90° [From 2]
∠OAB = 25°
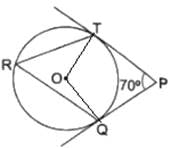
Q.3. In the given figure, O is the center of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70°, find ∠TRQ.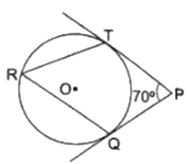
Given: In the figure, PT and PQ are two tangents and ∠TPQ = 70°
To Find: ∠TRQ
Construction: Join OT and OQ
In quadrilateral OTPQ
∠OTP = 90°
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
∠OQP = 90°
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
∠TPQ = 70° [Common]
By Angle sum of Quadrilaterals,
In quadrilateral OTPQ we have
∠OTP + ∠OQP + ∠TPQ + ∠TOQ = 360°
90° + 90° + 70° + ∠TOQ = 360°
250° + ∠TOQ = 360
∠TQO = 110°
Now,
As we Know the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
∴ we have
∠TOQ = 2∠TRQ
110° = 2 ∠TRQ
∠TRQ = 55°
Q.4. In the given figure, common tangents AB and CD to the two circles with centers O1 and O2 intersect at E. Prove that AB = CD.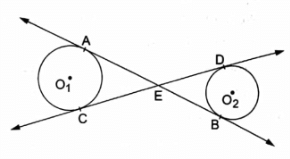
Given: AB and CD are two tangents to two circles which intersects at E .
To Prove: AB = CD
Proof:
As
AE = CE …[1]
[Tangents drawn from an external point to a circle are equal]
And
EB = ED …[2]
[Tangents drawn from an external point to a circle are equal]
Adding [1] and [2]
AE + EB = CE + ED
AB = CD
Hence Proved.
Q.5. If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.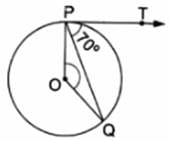
Given: PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°
To Find: ∠POQ = ?
Now,
∠OPT = 90°
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
∠OPQ + ∠QPT = 90°
∠OPQ + 70° = 90°
∠OPQ = 20°
Also,
OP = OQ [Radii of same circle]
∠OQP = ∠OPQ = 20°
[Angles opposite to equal sides are equal]
In △OPQ By Angle sum property of triangles,
∠OPQ + ∠OQP + ∠POQ = 180°
20° + 20° + ∠POQ = 180°
∠POQ = 140°
Q.6. In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4 cm and 3 cm respectively. If the area of ΔABC = 21 cm2 then find the lengths of sides AB and AC.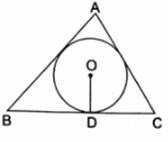
Given: △ABC that is drawn to circumscribe a circle with radius r = 2 cm and BD = 4 cm DC = 3cm
Also, area(△ABC) = 21 cm2
To Find: AB and AC
Now,
As we know tangents drawn from an external point to a circle are equal.
Then,
FB = BD = 4 cm [Tangents from same external point B]
DC = EC = 3 cm [Tangents from same external point C]
AF = EA = x (let) [Tangents from same external point A]
Using the above data, we get
AB = AF + FB = x + 4 cm
AC = AE + EC = x + 3 cm
BC = BD + DC = 4 + 3 = 7 cm
Now we have heron's formula for area of triangles if its three sides a, b and c are given
Where,
So, for △ABC
a = AB = x + 4
b = AC = x + 3
c = BC = 7 cm
⇒
And
Squaring both sides,
21(21) = 12x(x + 7)
12x2 + 84x - 441 = 0
4x2 + 28x - 147 = 0
As we know roots of a quadratic equation in the form ax2 + bx + c = 0 are,
So roots of this equation are,
but x = - 10.5 is not possible as length can't be negative.
So
AB = x + 4 = 3.5 + 4 = 7.5 cm
AC = x + 3 = 3.5 + 3 = 6.5 cm
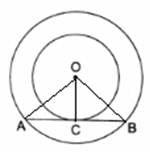
Q.7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle (in cm) which touches the smaller circle.
Given : Two concentric circles (say C1 and C2) with common center as O and radius r1 = 5 cm and r2 = 3 cm respectively.
To Find : Length of the chord of the larger circle which touches the circle C2. i.e. Length of AB.
As AB is tangent to circle C2 and,
We know that "Tangent at any point on the circle is perpendicular to the radius through point of contact"
So, we have,
OP ⏊ AB
∴ OPB is a right - angled triangle at P,
By Pythagoras Theorem in △OPB
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2 ]
We have,
(OP)2 + (PB)2 = (OB)2
r22 + (PB)2 = r12
(3)2 + (PB)2= (5)2
9 + (PB)2 = 25
(PB)2 = 16
PB = 4 cm
Now, AP = PB,
[ as perpendicular from center to chord bisects the chord and OP ⏊ AB ]
So,
AB = AP + PB = PB + PB
= 2PB = 2(4) = 8 cm
Q.8. Prove that the perpendicular at the point of contact of the tangent to a circle passes through the center.
Let us consider a circle with center O and XY be a tangent
To prove : Perpendicular at the point of contact of the tangent to a circle passes through the center i.e. the radius OP ⏊ XY
Proof :
Take a point Q on XY other than P and join OQ .
The point Q must lie outside the circle. (because if Q lies inside the circle, XY will become a secant and not a tangent to the circle).
∴ OQ is longer than the radius OP of the circle. That is,
OQ > OP.
Since this happens for every point on the line XY except the point P, OP is the
shortest of all the distances of the point O to the points of XY.
So OP is perpendicular to XY.
[As Out of all the line segments, drawn from a point to points of a line not passing through the point, the smallest is the perpendicular to the line.]
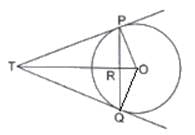
Q.9. In the given figure, two tangents RQ and RP are drawn from an external point R to the circle with center 0. If ∠PRQ = 120°, then prove that OR = PR + RQ.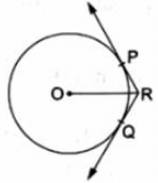
Given : In the figure ,
Two tangents RQ and RP are drawn from an external point R to the circle with center O and ∠PRQ = 120°
To Prove: OR = PR + RQ
Construction: Join OP and OQ
Proof :
In △△OPR and △OQR
OP = OQ [radii of same circle]
OR = OR [Common]
PR = PQ …[1]
[Tangents drawn from an external point are equal]
△OPR ≅ △OQR
[By Side - Side - Side Criterion]
∠ORP = ∠ORQ
[Corresponding parts of congruent triangles are congruent]
Also,
∠PRQ = 120°
∠ORP + ∠ORQ = 120°
∠ORP + ∠ORP = 120°
2∠ORP = 120°
∠ORP = 60°
Also, OP ⏊ PR
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
So, In right angled triangle OPR,
∴ OR = 2PR
OR = PR + PR
OR = PR + RQ [From 1]
Hence Proved.
Q.10. In the given figure, a circle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14 cm, BC = 8 cm and CA = 12 cm. Find the lengths AD, BE and CF.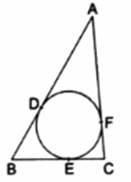
Let AD = x cm, BE = y cm and CF = z cm
As we know that,
Tangents from an external point to a circle are equal,
In given Figure we have
AD = AF = x
[Tangents from point A]
BD = BE = y
[Tangents from point B]6CF = CE = z [Tangents from point C]
Now, Given: AB = 14 cm
AD + BD = 14
x + y = 14
y = 14 - x … [1]
and BC = 8 cm
BE + EC = 8
y + z = 8
14 - x + z = 8 … [From 1]
z = x - 6 [2]
and
CA = 12 cm
AF + CF = 12
x + z = 12 [From 2]
x + x - 6 = 12
2x = 18
x = 9 cm
Putting value of x in [1] and [2]
y = 14 - 9 = 5 cm
z = 9 - 6 = 3 cm
So, we have AD = 9 cm, BE = 5 cm and CF = 3 cm
Q.11. In the given figure, 0 is the center of the circle. PA and PB are tangents. Show that AOBP is a cyclic quadrilateral.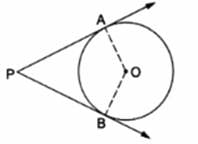
Given : PA and PB are tangents to a circle with center O
To show : AOBP is a cyclic quadrilateral.
Proof :
OB ⏊ PB and OA ⏊ AP
[Tangent at any point on the circle is perpendicular to the radius through point of contact]
∠OBP = ∠OAP = 90°
∠OBP + ∠OAP = 90 + 90 = 180°
AOBP is a cyclic quadrilateral
[ As we know if the sum of opposite angles in a quadrilateral is 180° then quadrilateral is cyclic ]
Hence Proved.
Q.12. In two concentric circles, a chord of length 8 cm of the larger circle touches the smaller circle. If the radius of the larger circle is 5 cm then find the radius of the smaller circle.
Let us consider circles C1 and C2 with common center as O. Let AB be a tangent to circle C1 at point P and chord in circle C2. Join OB
In △OPB
OP ⏊ AB
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
∴ OPB is a right - angled triangle at P,
By Pythagoras Theorem,
[i.e. (Hypotenuse)2 = (Base)2 + (Perpendicular)2]
(OB)2 = (OP)2 + (PB)2
Now, 2PB = AB
[As we have proved above that OP ⏊ AB and Perpendicular drawn from center to a chord bisects the chord]
2PB = 8 cm
PB = 4 cm
(OB)2 = (5)2 + (4)2
[As OP = 5 cm, radius of inner circle]
(OB)2 = 41
⇒ OB = √41 cm
Q.13. In the given figure, PQ is a chord of a circle with center 0 and PT is a tangent. If ∠QPT = 60°, find ∠P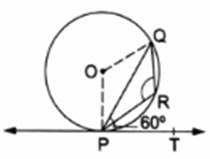
Given : , PQ is a chord of a circle with center 0 and PT is a tangent and ∠QPT = 60°.
To Find : ∠PRQ
∠OPT = 90°
∠OPQ + ∠QPT = 90°
∠OPQ + 60° = 90°
∠OPQ = 30° … [1]
Also.
OP = OQ [radii of same circle]
∠OQP = ∠OPQ [Angles opposite to equal sides are equal]
From [1], ∠OQP = ∠OQP = 30°
In △OPQ , By angle sum property
∠OQP + ∠OPQ + ∠POQ = 180°
30° + 30° + ∠POQ = 180°
∠POQ = 120°
As we know, the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
So, we have
2∠PRQ = reflex ∠POQ
2∠PRQ = 360° - ∠POQ
2∠PRQ = 360° - 120° = 240°
∠PRQ = 120°
Q.14. In the given figure, PA and PB are two tangents to the circle with center O. If ∠APB = 60° then find the measure of ∠OAB.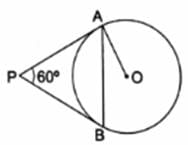
In the given figure, PA and PB are two tangents from common point P
∴ PA = PB
[∵ Tangents drawn from an external point are equal]
∠PBA = ∠PAB
[∵ Angles opposite to equal angles are equal] …[1]
By angle sum property of triangle in △APB
∠APB + ∠PBA + ∠PAB = 180°
60° + ∠PAB + ∠PAB = 180° [From 1]
2∠PAB = 120°
∠PAB = 60° …[2]
Now,
∠OAP = 90° [Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
∠OAB + ∠PAB = 90°
∠OAB + 60° = 90° [From 2]
∠OAB = 30°
|
53 docs|15 tests
|
|
Dec 26, 2024 Last updated |
|
53 docs|15 tests
|
|
Explore Courses for Class 10 exam
|
|
Semester Notes
,MCQs
,mock tests for examination
,RS Aggarwal Solutions: Circles- 1 | RS Aggarwal Solutions for Class 10 Mathematics
,Sample Paper
,Objective type Questions
,Important questions
,Extra Questions
,RS Aggarwal Solutions: Circles- 1 | RS Aggarwal Solutions for Class 10 Mathematics
,practice quizzes
,Viva Questions
,study material
,RS Aggarwal Solutions: Circles- 1 | RS Aggarwal Solutions for Class 10 Mathematics
,Free
,video lectures
,past year papers
,shortcuts and tricks
,Summary
,ppt
,Exam
,Previous Year Questions with Solutions
;
RS Aggarwal Solutions: Circles- 1 Free PDF Download
Importance of RS Aggarwal Solutions: Circles- 1
RS Aggarwal Solutions: Circles- 1 Notes
RS Aggarwal Solutions: Circles- 1 Class 10 Questions
Study RS Aggarwal Solutions: Circles- 1 on the App
|
© EduRev
|
Education Revolution
|
|
