RS Aggarwal Solutions: Constructions- 1 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
Exercise: 13a
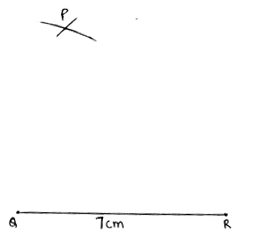
Q.1. Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that  .
.
Steps of Construction:
1. Draw a line segment AB of given length 7cm.
2. Draw a line originating from A and making an acute angle with line segment AB.
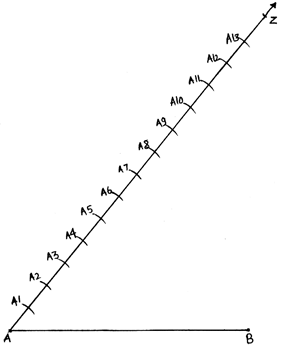
3. As we have to get 3 parts out of 5 parts of AB. We will divide the line from A into 5 parts.
4. Taking A as center draw an arc cutting at A1 on the line.
5. With the same radius and taking A1 as a center, draw another arc cutting line at A2. Repeat the same till A5, as shown below:
6. Join A5 and B by drawing a line:
7. Draw lines parallel to A5B from A4, A3, A3 and A1 cutting line AB.
8. The Point where the parallel line from A3 cuts AB is P.
9. Hence P is the required point such that AP/AB = 3/5.
Q.2. Draw a line segment of length 7. 6 cm and divide it in the ratio 5:8. Measure the two parts.
Steps of Construction:
1. Draw a line segment AB of length 7. 6cm.
2. Draw a ray AZ making an acute angle with the line AB.
3. As we have to divide the line in the ratio of 5:8. So we will make 5+8 = 13 points along AX.
4. Along AX we mark 13 arcs taking A as starting point for the first, A1 as starting point for second and so on till A13.
5. Join the A13B.
6. With the help of these arcs, this line can be divided into 13 equal points.
7. In our case of 5:8, we join the 5th point i. e. A5 with the line AB such that the line A5P is parallel to line A13B.
8. P is the required point, the point that divides the line in a ratio of 5:8.
Length of AP = 2. 9cm (approximately )
Length of PB = 4. 7cm (approximately )
AP+PB = 2. 9+4. 7 = 7. 6 = AB.
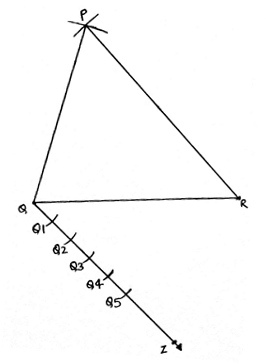
Q.3. Construct a ΔPQR, in which PQ = 6 cm, QR = 7 cm and PR = 8 cm. Then, construct another triangle whose sides are 4/5 times the corresponding sides of ΔPQR.
Steps of Construction:
1. First, we draw the triangle ABC of given dimensions.
2. Draw a line segment QR of length 7cm.
3. With Q as center draw an arc of radius 6cm(length of PQ).
4. With R as center draw an arc of radius 8cm(length of PR).
5. The point where the arcs intersect each other is P. Join PQ and PR.
6. Now we construct the triangle having dimensions of 4/5 of this triangle.
7. Draw a ray AZ at an acute angle to the line QR in the other direction of P.
8. Make 5 equal arcs along QZ, taking Q as starting point for the first arc, Q1 for second and so on till Q5. Join Q5R.
9. As we have to get the 4/5 dimensions of this triangle. We draw a line parallel to QR from Q4 till QR. This point is R’.
10. Now from R’, draw another line parallel to PR cutting PQ at P’.
11. P’QR’ is the required triangle.
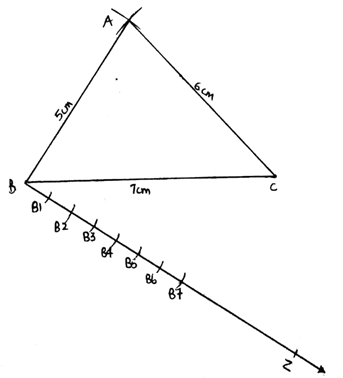
Q.4. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle.
Steps of Construction:
1. First, we have drawn a triangle of given dimensions, let’s say the triangle is ABC as in figure 1.
2. Draw a line segment BC of length 7cm.
3. Make an arc of radius 5cm taking B as a center.
4. Similarly, draw an arc of 6 cm taking C as center cutting the first arc at A.
5. Join AB and AC.
6. Now we have to make a triangle which is 7/5 times of this triangle. That is we have to make a bigger triangle.
7. Draw a ray BZ making an acute angle with BC. Make 7 equal arcs along BZ starting from B then B1 and so on till B7.
8. Join B5C. Extend the line segment BC in the direction of C.
9. Draw a line from B7 parallel to B5C cutting the extended BC at C’.
10. Extend BA along A. Draw a line from C’ parallel to CA cutting the extended line BA at A’.
11. Then A’BC’ is the required triangle.
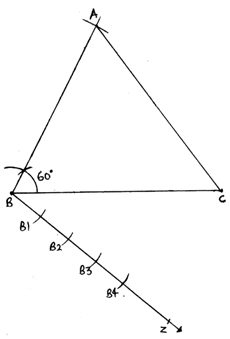
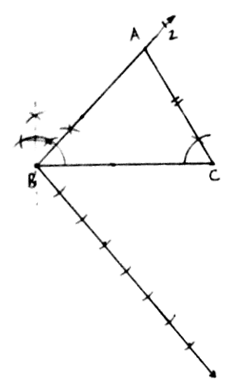
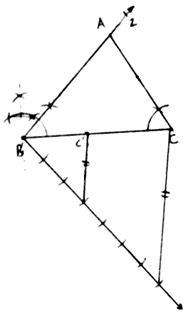
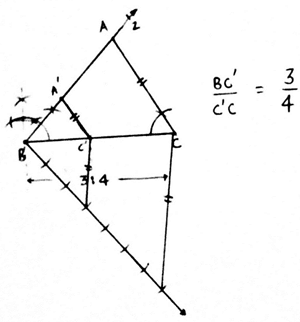
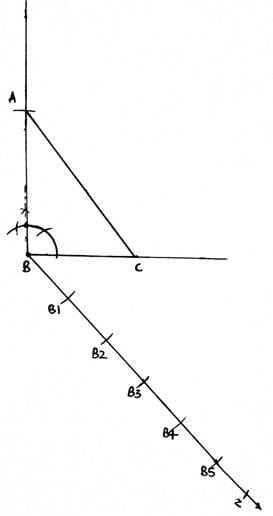
Q.5. Construct a ΔABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are 3/4 times the corresponding sides of ΔABC.
Steps of Construction:
1. First, we draw a triangle ABC of given dimensions.
2. Draw a line segment BC of length 7cm.
3. From B, make an angle of 60° and draw a ray from B.
4. Now taking B as center and radius of 6cm(length of AB), draw an arc on the ray. The point is A.
5. Join AC.
6. Now we have to make a triangle which is 3/4 times of this triangle.
7. Draw a ray BZ making an acute angle with the line BC. Make 4 equal arcs starting from B then B1 and so on till B4.
8. Join B4C. Draw a line from B3 parallel to B4C cutting BC at C’.
9. Draw another line from C’ parallel to CA cutting AB at A’.
10. A’BC’ is our required triangle,
Q.6. Construct a ΔABC in which AB = 6 cm, ∠A = 30° and ∠B = 60°. Construct another ΔAB' C' similar to ΔABC with base AB' = 8 an.
Steps of Construction:
1. Draw a line AB of length 6cm and extend it to B’ such that AB’ is of length 8 cm.
2. Make an angle of 30° from A and angle of 60° from B. The point where these extended rays meet is C.
3. As angles are equal in similar triangles, make an angle of 60° from B’ as well.
4. Extend the line AC along C such that it cuts the ray from B’ at C’.
5. AB’C’ is the required triangle .
Q.7. Construct a ΔABC in which BC = 8 cm, ∠B = 45° and ∠C = 60°. Construct another triangle similar to ΔABC such that its sides are 3/5 of the corresponding sides of ΔABC.
Steps of Construction:
1. Draw a line segment BC of length 8cm.
2. Make an angle of 45° from B and an angle of 60° from C. The point where the rays meet is point A.
3. Draw a ray BY making an acute angle with the line BC. Make 5 equal arcs starting from B, then B1 and so on till B5.
4. Join B5C.
5. As we have to get the triangle 3/5 times of this triangle ABC.
6. From B3, draw a line parallel to B5C cutting BC at C’.
7. Draw another line from C’ parallel to AC cutting AB at A’.
8. A’BC’ is our required triangle.
Q.8. To construct a triangle similar to ΔABC in which BC = 4. 5 cm, ∠B = 45° and ∠C = 60°, using a scale factor of 3/7, BC will be divided in the ratio
(a) 3 : 4 (b) 4:7 (c) 3 : 10 (d) 3 : 7
Steps of Construction:
1. First we construct the triangle ABC with the given dimensions.
2. Draw a line segment BC of length 4. 5 cm. Make an angle of 45° from B and an angle 60° from C.
3. The point where the rays meet is A.
4. Now draw a ray making an acute angle with BC. Make 7 equal arcs.
5. Join the last arc cut point with C and from 3rd arc, cut point draw a line parallel to B7C cutting BC at C’.
6. From C’ draw a line parallel to AC cutting AB at A’.
A’BC’ is or required triangle.
7. Now we see that our line BC gets divided into the ratio of 3:4.
So (a) 3:4 is the answer.
Q.9. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are  times the corresponding sides of the isosceles triangle.
times the corresponding sides of the isosceles triangle.
Steps of Construction:
1. Draw a line segment BC of length 8cm.
2. Now as we know that the altitude of the isosceles triangle is also the bisector of the baseline. So we draw a perpendicular bisector of line BC.
3. We cut an arc of length 4cm( length of altitude). The arc cut point is A.
4. Join AB and AC.
5. Now we have draw a triangle which is 3/2 times of this triangle that a triangle which is bigger than this.
6. So we extend BC along C and BA along A as in figure.
7. Draw a ray BZ making an acute angle with BC. Make 3 equal arcs along BZ.
7. Join the second arc with C. Now draw a line from last arc cut point parallel to the previous line cutting the extended BC at C’.
8. From C’ draw another line parallel to CA cutting the extended BY at A’.
9. A’BC’ is our required triangle.
Q.10. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then, construct another triangle whose sides are 3/5 times the corresponding sides of the given triangle.
Steps of Construction:
1. First we have to draw a triangle of given dimensions lets say ABC.
2. Draw a line segment of length BC of length 3cm.
3. Make an angle of 90° at B and cut an arc of radius 4cm taking B as center. The Arc cut point is A.
4. Join AC. ABC is the right angled triangle with the given dimensions.
5. Now we have to make a triangle which 5/3 times of this triangle, that is bigger than this triangle.
6. So we extend the line BC along C and BA along A.
7. Draw a ray BZ making an acute angle with BC. Make 5 equal arcs along BZ starting from B then B1 and so on till B5.
8. Join B3C. From B5 draw a ray parallel to B3C cutting the extended BC at C’.
9. From C’, draw another ray parallel to CA cutting the extended BA at A’.
10. Then A’BC’ is our required triangle.
Exercise: 13b
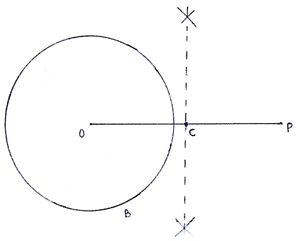
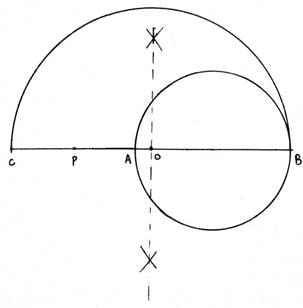
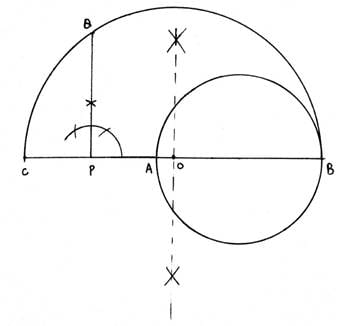
Q.1. Draw a circle of radius 3 cm. From a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents.
Steps of Construction:
1. Draw a circle of radius 3 cm taking O as center.
2. Mark a point P, 7 cm far from point O. Draw OP.
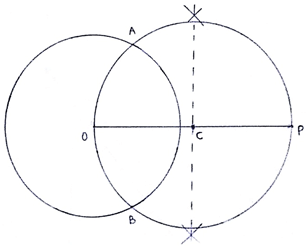
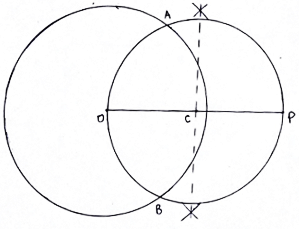
3. Draw a perpendicular bisector of OP. The bisector cuts OP at C.
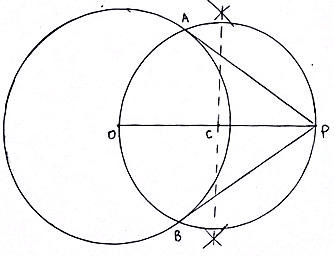
4. Taking C as center and radius equal to length OC or CP, draw a circle.
5. Both circles intersect at points A and B.
6. Join AP and BP. Then AP and BP are the required tangents.
Q.2. Draw two tangents to a circle of radius 3.5 cm from a point P at a distance of 6.2 cm from its centre.
Steps of Construction:
1. Draw a circle of radius 3. 5 cm taking O as center.
2. Mark a point P, 6. 2 cm far from point O. Draw OP.
3. Draw a perpendicular bisector of OP. The bisector cuts OP at C.
4. Taking C as center and radius equal to length OC or CP, draw a circle.
5. Both circles intersect at points A and B.
6. Join AP and BP. Then AP and BP are the required tangents.
Q.3. Draw a circle of radius 3.5 cm. Take two points A and B on one of its extended diameter, each at a distance of 5 cm from its centre. Draw tangents to the circle from each of these points A and B.
Steps of Construction:
1. Draw a circle of radius 3.5 cm taking O as the center.
2. Extend any diameter of the circle. On the extended diameter, mark two points in two directions, A and B such that OA = OB = 5 cm.
3. Draw perpendicular bisector of OA. The bisector cuts OA at P.
4. Draw perpendicular bisector of OB. The bisector cuts OB at Q.
5. Taking P as center and radius equal to length OP or PA, draw a circle.
6. The two circles intersect each other at K and L.
7. Join AK and AL. AK and AL are the required tangents from point A.
8. Now, Taking Q as center and radius equal to length OQ or QB, draw a circle.
9. The circle with center O and center Q intersect each other at M and N.
10. Join BM and BN. BM and BN are the required tangents from point B.
Q.4. Draw a circle with centre O and radius 4 cm. Draw any diameter AB of this circle. Construct tangents to the circle at each of the two end points of the diameter AB.
Steps of construction:
1. Draw a circle of radius 4 cm taking O as center.
2. Draw a diameter AB of this circle.
3. As we know that the tangents make an angle of 90° with the radius of the circle.
4. We draw ∠OAC = 90° at A. Produce CA to D. CD is the required tangent.
5. We draw ∠OBE = 90° at B. Produce EB to F. EF is the required tangent.
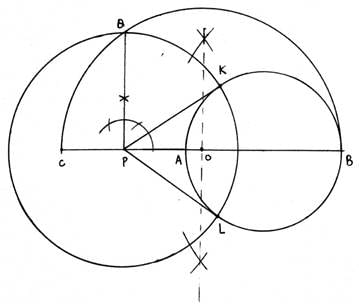
Q.5. Draw a circle with the help of a bangle. Take any point P outside the circle. Construct the pair of tangents from the point P to the circle. HINT See Example 6.
Steps of Construction:
1. Draw a circle with the help of a bangle. (implies center and radius of the circle is unknown)
2. Mark a point P outside the circle.
3. Draw a secant to this circle , PAB that intersect the circle at A and B.
4. Extend AP to C, such that PA = PC.
5. Draw perpendicular bisector of CB, which intersects CB at O.
6. With O as center, draw a semicircle passing through C and B.
7. From P, make an angle of 90° such that it cuts the semicircle at Q.
8. With P as center and PQ as the radius of the circle. Draw a circle that cuts the previous circle at K and L.
9. Join PK and PL. Then PK and PL are the required tangents.
Q.6. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Steps of Construction:
1. Draw a line segment AB of length 8cm.
2. With A as center, draw a circle with radius of length equal to 4cm.
3. With B as center , draw a circle with radius of length equal to 3cm.
4. Draw perpendicular bisector of AB, which cuts AB at O.
5. With O as center and radius equal to OA(or OB), draw a circle.
6. The Circle of center O cuts the center of center A at C and D.
7. Join BC and BD. Then BC and BD are the required tangents.
8. The circle of center O cuts a circle of center B at E and F.
9. Join AE and AF. Then AE and AF are the required tangents.
Q.7. Draw a circle of radius 4.2 cm. Draw a pair of tangents to this circle inclined to each other at an angle of 45°.
Steps of Construction:
1. Draw a circle with center O and radius of length 4. 2cm.
2. We then draw any diameter POQ of this circle.
3. We then draw an angle ROQ = 45°.
4. Draw angle of 90° from P and R.
5. Extend both the rays. The point where both the points intersect is S.
6. Then PS and RS are the required tangents.
Q.8. Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm, which are inclined to each other at an angle of 60°.
Steps of Construction:
1. Draw a circle with center O and radius of length 3cm.
2. We then draw any diameter POQ of this circle.
3. We then draw an angle ROQ = 60°.
4. Draw angle of 90° from P and R.
5. Extend both the rays. The point where both the points intersect is S.
6. Then PS and RS are the required tangents.
Q.9. Draw a circle of radius 3 cm. Draw a tangent to the circle making an angle of 30° with a line passing through the centre.
Steps of Construction:
1. Draw a circle with center O and radius of length 3cm.
2. Draw any radius OP of this circle.
3. Extend OP to Q.
4. Draw angle AOP = 60°.
5. From A, draw angle of 90°.
6. The two lines intersect each other at B.
7. Then BA is the required tangent.
Q.10. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Steps of Construction:
1. With O as center, draw a circle of radius of 4cm and another circle of radius 6cm.
2. Mark any point A on the bigger circle.
3. Join OA. Draw perpendicular bisector of OA.
4. The perpendicular bisector XY of OA intersects OA at B.
5. With B as center and radius of length OB (or BA), draw a circle.
6. This circle intersects the smaller circle(of radius 4cm) at P and Q.
7. Join AP and AQ.
8. Then AP and AQ are the required tangents.
|
53 docs|15 tests
|
|
53 docs|15 tests
|

|
Explore Courses for Class 10 exam
|

|