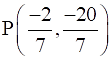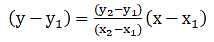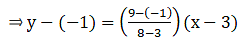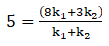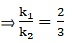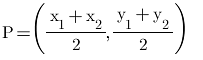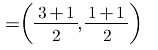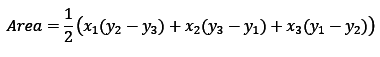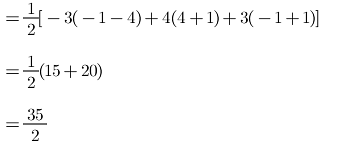RS Aggarwal Solutions: Coordinate Geometry- 2 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download

Q.1. Find the coordinates of the point which divides the join of A(– 1, 7) and B(4, – 3) in the ratio 2 : 3.

Let the point P(x, y) divides AB

Then
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (2 × 4 + 3 × (– 1))/2 + 3
= (8 – 3) /5
= 5/5 = 1
Y = (m₁y₂ + m₂y1)/ m₁ + m₂
= (2 × (– 3) + 3 × 7)/ 5
= (– 6 + 21)/5
= 15 / 5 = 3
= (1, 3)

Q.2. Find the coordinates of the point which divides the join of A(– 5, 11) and B(4, – 7) in the ratio 7 : 2.

Let the point P(x, y) divides AB

Then
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (7 × 4 + 2 × (– 5))/7 + 2
= (28 – 10) /9
= 18/9 = 2
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (7 × (– 7) + 2 × 11)/ 9
= (– 49 + 22)/9
= – 27 / 9 = – 3
= (2, – 3)

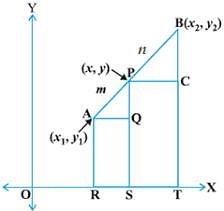
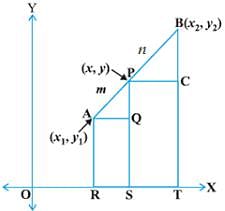
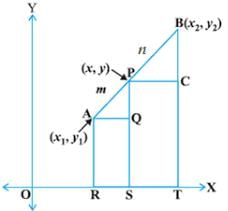
Q.3. If the coordinates of points A and B are (– 2, – 2) and (2, – 4) respectively, find the coordinates of the point P such that AP = 3/7 AB, where P lies on the line segment AB.

Let the point P(x, y) divides AB

Then
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (3 × 2) + 4x (– 2))/ 3 + 4
= (6 – 8)/7
= – 2/7
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (3 × (– 4) + 4 × (– 2))/ 7
= (– 12 – 8)/ 7
= – 20 / 7

Q.4. Point A lies on the line segment PQ joining P(6, – 6) and Q(– 4, – 1) in such a way that 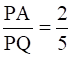.  If the point A also lies on the line 3x + k(y + 1) = 0, find the value of k.

Let the point P(x, y) divides AB
Then
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (2 × (– 4) + 3 × 6)/2 + 3
= (– 8 + 18) /5
= 10/5 = 2
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (2 × (– 1) + 3 x( – 6))/ 5
= (– 2 – 18)/5
= – 20 / 5 = – 4
If the point A also lies on the line 3x + k(y + 1) = 0
Then
3 × 2 + k(– 4 + 1) = 0
6 – 3k = 0
6 = 3k
k = 2

Q.5. Points P, Q, R and S divide the line segment joining the points A(1, 2) and B(6, 7) in five equal parts. Find the coordinates of the points P, Q and R.

P divides the segment AB in ratio 1:4
Q divides the segment AB in ratio 2:3
R divides the segment AB in ratio 3:2
For coordinates of P
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × 6 + 4 × 1)/1 + 4
= (6 + 4) /5
= 10/5 = 2
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1x 7 + 4 × 2)/5
= (7 + 8)/5
= 15 / 5 = 3
= (2, 3)
For coordinates of Q
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (2x 6 + 3x 1)/5
= (12 + 3) /5
= 15/5 = 3
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (2 × 7 + 3 × 2)/ 5
= (14 + 6)/5
= 20 / 5 = 4
= (3, 4)
For coordinates of R
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (3 × 6 + 2 × 1)/5
= (18 + 2) /5
= 20/5 = 4
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (3 × 7 + 2 × 2)/ 5
= (21 + 4)/5
= 25 / 5 = 5
= (4,5)
Hence P(2, 3), Q(3, 4), R(4, 5)

Q.6. Points P, Q and R in that order are dividing a line segment joining A(1, 6) and B(5, – 2) in four equal parts. Find the coordinates of P, Q and R.

P divides the segment AB in ratio 1:3
Q divides the segment AB in ratio 2:2
R divides the segment AB in ratio 3:1
For coordinates of P
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × 5 + 3 × 1)/1 + 3
= (5 + 3) /4
= 8/4 = 2
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1× (– 2) + 3 × 6)/4
= (– 2 + 18)/5
= 16 / 4 = 4
= (2, 4)
For coordinates of Q
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (2x 5 + 2x 1)/4
= (10 + 2) /4
= 12/4 = 3
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (2 × (– 2) + 2 × 6)/ 4
= (– 4 + 12)/4
= 8 / 4 = 2
= (3,2)
For coordinates of R
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (3x 5 + 1x 1)/4
= (15 + 1) /4
= 16/4 = 4
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (3 × (– 2) + 1 × 6)/ 4
= (– 6 + 6)/4
= 0/ 4 = 0
= (4,0)
∴ the coordinates are P(2, 4), Q(3, 2), R (4, 0)

Q.7. The line segment joining the points A(3, – 4) and B(1, 2) is trisected at the points P(p, – 2) and Q(5/3, q). Find the values of p and q.

P divides the segment AB in ratio 1:2
Q divides the segment AB in ratio 2:1
For coordinates of P
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × 1 + 2 × 3)/1 + 2
= (1 + 6) /3
= 7/3 = p
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1x2 + 2 × (– 4))/3
= (2 – 8)/3
= – 6/ 3 = – 2
For coordinates of Q
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (2x 1 + 1x 3)/3
= (2 + 3) /3
= 5/3
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (2 × 2 + 1 × (– 4))/3
= (4 – 4)/3
= 0/ 3
= 0 = q
p = 7/3 , q = 0

Q.7. Find the coordinates of the midpoint of the line segment joining
A(3, 0) and B (– 5, 4)

X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × (– 5) + 1x 3)/1 + 1
= (– 5 + 3) /2
= – 2/2 = – 1
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1x 4 + 1x 0)/2
= (4 + 0)/2
= 4 / 2 = 2
(– 1, 2)

Q.9. Find the coordinates of the midpoint of the line segment joining
P(– 11, – 8) and Q(8, – 2).

X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × 8 + 1x (– 11)/1 + 1
= (8 – 11) /2
= – 3/2
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1x (– 2) + 1x – 8)/2
= (– 2 – 8)/2
= – 10 / 2 = – 5

Q.10. If (2, p) is the midpoint of the line segment joining the points A(6, – 5) and B(– 2, 11), find the value of p.

X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × (– 2) + 1x 6)/1 + 1
= (– 2 + 6) /2
= 4/2 = 2
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1x 11 + 1x (– 5))/2
= (11 – 5)/2
= 6 / 2 = 3
p = 3

Q.11. The midpoint of the line segment joining A(2a, 4) and B(– 2, 3b) is C(1, 2a + 1). Find the values of a and b.

X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × (– 2) + 1× 2a)/1 + 1
= (– 2 + 2a) /2
(– 2 + 2a)/2 = 1
– 2 + 2a = 2
2a = 4
a = 2
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1 × 3b + 1 ×4)/2
= (3b + 4)/2
(3b + 4)/2 = 2a + 1
(3b + 4)/2 = 5
(3b + 4) = 10
3b = 6
b = 2
a = 2, b = 2

Q.12. The line segment joining A(– 2, 9) and B(6, 3) is a diameter of a circle with centre C. Find the coordinates of C.

X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × 6 + 1x (– 2)/1 + 1
= (6 – 2) /2
= 4/2 = 2
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1x 3 + 1x 9)/2
= (3 + 9)/2
= 12 / 2 = 6
C(2, 6)

Q.13. Find the coordinates of a point A, where AB is a diameter of a circle with centre C(2, – 3) and the other end of the diameter is B(1, 4).

Let the coordinates of A be × & y. So A(X,Y) and B(1,4)
2 = (m₁x₂ + m₂x₁)/ m₁ + m₂
2 = (1 × 1 + 1 × X)/1 + 1
2 = (1 + X) /2
1 + X = 4
× = 3
– 3 = (m₁y₂ + m₂y₁)/ m₁ + m₂
– 3 = (1× 4 + 1 × Y)/2
– 3 = (4 + Y)/2
(4 + Y) = – 6
Y = – 10
A(3, – 10)

Q.14. In what ratio does the point P(2, 5) divide the join of A(8, 2) and B(– 6, 9)?

2 = (m₁x₂ + m₂x₁)/ m₁ + m₂
2 = (m₁ × (– 6) + m₂ 8)/ m₁ + m₂
2 = (– 6m₁ + 8m₂ ) / m₁ + m₂
– 6m₁ + 8m₂ = 2(m₁ + m₂ )
– 8m₁ + 6m₂ = 0
5 = (m₁y₂ + m₂y₁)/ m₁ + m₂
5 = (m₁ × 9 + m₂ 2)/ m₁ + m₂
5 = (9m₁ + 2m₂ ) / m₁ + m₂
9m₁ + 2m₂ = 5(m₁ + m₂)
4m₁ + 3m₂ = 0
Solving for m₁ and m₂ we get
m₁ = 3
m₂ = 4
3 : 4

Q.15. Find the ratio in which the point 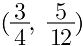 divides the line segment joining the points  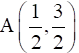and B(2, – 5).

3/4 = (m₁x₂ + m₂x₁)/ m₁ + m₂
3/4 = (m₁ × 2 + m₂ (1/2))/ m₁ + m₂
3/4 = (2m₁ + m₂ /2) / m₁ + m₂
6m₁ + 6m₂ = 16m₁ + 4m₂
6m₁ – 2m₂ = 0
5/12 = (m₁y₂ + m₂y₁)/ m₁ + m₂
5/12 = (m₁ × (– 5) + m₂ (3/2))/ m₁ + m₂
5/12 = (– 5m₁ + 3m₂ /2) / m₁ + m₂
– 120m₁ + 36m₂ = 10(m₁ + m₂)
130m₁ – 26m₂ = 0
Solving for m₁ and m₂ we get
m₁ = 1
m₂ = 5
1 : 5

Q.16. Find the ratio in which the point P(m, 6) divides the join of A(– 4, 3) and B(2, 8). Also, find the value of m.

6 = (m₁y₂ + m₂y₁)/ m₁ + m₂
6 = (m₁ × 8 + m₂ 3)/ m₁ + m₂
6 = (8m₁ + 3m₂ ) / m₁ + m₂
8m₁ + 8m₂ = 6(m₁ + m₂)
2m₁ – 3m₂ = 0
m₁:m₂ = 3:2
Now,
m = (m₁x2 + m₂x₁)/ m₁ + m₂
m = (m₁ × 2 + m₂ (– 4))/ m₁ + m₂
m = (2m₁ – 4m₂ ) / m₁ + m₂
2m₁ – 4m₂ = m(m₁ + m₂ )
Putting the values of m₁ & m₂
m = – 2/5
Hence, 3:2, m = – 2/5

Q.17. Find the ratio in which the point (– 3, k) divides the join of A(– 5, – 4) and B(– 2, 3). Also, find the value of k.

– 3 = (m₁x₂ + m₂x₁)/ m₁ + m₂
– 3 = (m₁ × (– 2) + m₂ (– 5))/ m₁ + m2
– 3 = (– 2m₁ – 5m₂ ) / m₁ + m₂
– 2m₁ – 5m₂ = – 3(m₁ + m₂ )
2m₁ + 5m₂ = 3(m₁ + m₂ )
m₁ – 2m₂ = 0
m₁:m₂ = 1:2
Now,
K = (m₁y₂ + m₂y₁)/ m₁ + m₂
K = (m₁ × 3 + m₂(– 4))/ m₁ + m₂
K = (3m₁ – 4m₂ ) / m₁ + m₂
3m₁ – 4m₂ = k(m₁ + m₂)
Putting the values of m₁ & m₂
k = 2/3
Hence, 2:1, k = 2/3

Q.18. In what ratio is the line segment joining A(2, – 3) and B(5, 6) divided by the x – axis? Also, find the coordinates of the point of division.

The segment is divided by x – axis i.e the coordinates are (x, 0)
x = (m₁x₂ + m₂x₁)/ m₁ + m₂
x = (m₁ × 5 + m₂ 2)/ m₁ + m₂
x = (5m₁ + 2m₂ ) / m₁ + m₂
5m₁ + 2m₂ = x(m₁ + m₂ )
(5 – x)m₁ + (2 – x)m₂ = 0
0 = (m₁y₂ + m₂y₁)/ m₁ + m₂
0 = (m₁ × 6 + m₂(– 3))/ m₁ + m₂
0 = (6m₁ – 3m₂ ) / m₁ + m₂
6m₁ – 3m₂ = 0
Solving for m₁ and m₂ we get
m₁ = 1
m₂ = 2
(1 : 2),
Putting the values of m₁ and m₂
x = 3
Hence coordinates are (3, 0)

Q.19. In what ratio is the line segment joining the points A(– 2, – 3) and B(3, 7) divided by the y – axis? Also, find the coordinates of the point of division.

The segment is divided by y – axis i.e the coordinates are (0, y)
0 = (m₁x₂ + m₂x₁)/ m₁ + m₂
0 = (m₁ × 3 + m₂ (– 2))/ m₁ + m₂
0 = (3m₁ – 2m₂ ) / m₁ + m₂
3m₁ – 2m₂ = 0
m₁ = 2
m₂ = 3
(2 : 3)
y = (m₁y₂ + m₂y₁)/ m₁ + m₂
y = (m₁ × 7 + m₂(– 3))/ m₁ + m₂
y = (7m₁ – 3m₂ ) / m₁ + m₂
7m₁ – 3m₂ = y(m₁ + m₂)
Putting the values of m₁ and m₂
y = 1

Q.20. In what ratio does the line x – y – 2 = 0 divide the line segment joining the points A (3, –1) and B(8, 9)?

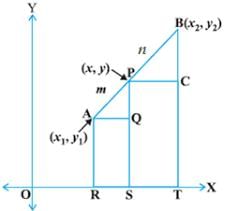
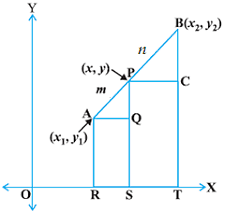
The line segment joining any two points (x1, y1) and (x2, y2) y2 is given as:


⇒ y + 1 = 10/5 (x-3)
⇒ y + 1 = 2(x-3)
⇒ y + 1 = 2x – 6
⇒ 2x – y = 7..eq(1) is the equation of line segment.
Now, we have to find the point of intersection of eq (1) & the given line: x – y- 2 = 0
2x – y = 7
& x – y – 2 = 0
2x – 7 = x – 2
⇒ x = 7- 2
⇒ x = 5
And, y = 3
Let us say this point divides the line segment in the ratio of k₁:k₂
Then,

⇒ 5k₁ + 5k₂ = 8k₁ + 3k₂
⇒ 5k₁ - 8k₁ + 5k₂ - 3k₂= 0
⇒ -3k₁ + 2k₂ = 0

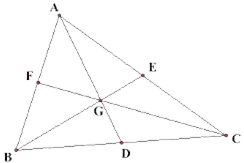
Q.21. Find the lengths of the medians of a ΔABC whose vertices are A(0, – 1), B(2, 1) and C(0, 3).

For coordinates of median AD segment BC will be taken
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × 0 + 1x 2)/1 + 1
= (0 + 2) /2
= 2/2 = 1
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1x 3 + 1x 1)/2
= (3 + 1)/2
= 4 / 2 = 2
D(1,2)
By distance Formula
AD = √(1 – 0)² + (2 + 1)²
= √1 + 9
= √10
For coordinates of BE, segment AC will be taken
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × 0 + 1x 0)/1 + 1
= (0 + 0) /2
= 0/2 = 0
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1x 3 + 1x (– 1))/2
= (3 – 1)/2
= 2 / 2 = 1
∴ E(0, 1)
By distance Formula
BE = √(0 – 2)² + (1 – 1)²
= √4 + 0
= √4 = 2
For coordinates of median CF segment AB will be taken
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × 2 + 1x 0)/1 + 1
= (2 + 0) /2
= 2/2 = 1
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1x(– 1) + 1x 1)/2
= (– 1 + 1)/2
= 0 / 2 = 0
F(1, 0)
By distance Formula
CF = √(1 – 0)² + (0 – 3)²
= √1 + 9
= √1
AD = √10 units, BE = 2 units, CF = √10 units

Q.22. Find the centroid of ΔABC whose vertices are A(– 1, 0), B(5, – 2) and C(8, 2)

First we need to calculate the coordinates of median
For coordinates of median AD segment BC will be taken
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (1 × 8 + 1x 5)/1 + 1
= (8 + 5) /2
= 13/2
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (1x 2 + 1x (– 2))/2
= (0)/2
= 0 / 2 = 0
D(13/2,0)
The centroid of the triangle divides the median in the ratio 2:1
By section formula,
X = (m₁x₂ + m₂x₁)/ m₁ + m₂
= (2 × 13/2 + 1x (– 1))/2 + 1
= (13 – 1) /3
= 12/3 = 4
Y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (2x 0 + 1x 0)/2 + 1
= 0/3
= 0
∴ G coordinate is (4, 0)

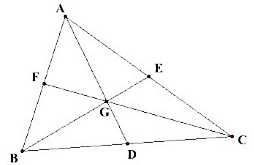
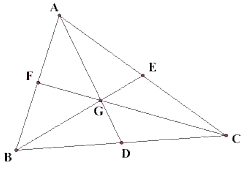
Q.23. If G(– 2, 1) is the centroid of a ΔABC and two of its vertices are A(1, – 6) and B(– 5, 2), find the third vertex of the triangle.

The figure is shown as:

– 2 = (m₁x₂ + m₂x₁)/ m₁ + m₂
– 2 = (2 × x + 1x 1)/2 + 1
– 2 = (2x + 1) /3
– 6 = 2x + 1
– 7 = 2x
⇒ x = – 7/2
1 = (m₁y₂ + m₂y₁)/ m₁ + m₂
1 = (2x y + 1x (– 6))/3
1 = (2y – 6)/2
2 = 2y – 6
8 = 2y
⇒ y = 4
D(– 7/2,4)
Now for BC
– 7/2 = (m₁x₂ + m₂x₁)/ m₁ + m₂
– 7/2 = (1 × x + 1x (– 5))/1 + 1
– 7/2 = (x – 5) /2
– 7 = x – 5
– 7 + 5 = x
⇒ x = – 2
4 = (m₁y₂ + m₂y₁)/ m₁ + m₂
4 = (1 × y + 1x 2)/2
4 = (y + 2)/2
8 = y + 2
⇒ y = 6
Hence, C(– 2, 6)

Q.24. Find the third vertex of a ΔABC if two of its vertices are B(– 3, 1) and C(0, – 2), and its centroid is at the origin.

Coordinate of D on median on BC
x = (m₁x₂ + m₂x₁)/ m₁ + m₂
x = (1 × 0 + 1x (– 3))/1 + 1
x = (0 – 3) /2
x = – 3/2
y = (m₁y₂ + m₂y₁)/ m₁ + m₂
y = (1 × (– 2) + 1x 1)/2
y = (– 2 + 1)/2
2y = – 1
y = – 1/2
D(– 3/2, – 1/2)
Now for AD we have D(– 3/2, – 1/2) and Centroid C(0,0)
0 = (m₁x₂ + m₂x₁)/ m₁ + m₂
0 = (2 × (– 3/2) + 1x x)/2 + 1
0 = (– 3 + x) /3
– 3 + x = 0
x = 3
0 = (m₁y₂ + m₂y₁)/ m₁ + m₂
0 = (2 × (– 1/2) + 1x y)/2 + 1
0 = (– 1 + y)/3
– 1 + y = 0
y = 1
Hence, A(3, 1)

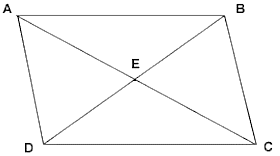
Q.25. Show that the points A(3,1), B(0, – 2), C(1, 1) and D(4, 4) are the vertices of a parallelogram ABCD.

We know that if diagonals of a quadrilateral bisect each other, then the quadrilateral is parallelogram
Given,
A(3, 1), B(0, -2), C(1, 1) and D(4, 4) are coordinates of a quadrilateral
So,
If ABCD is a parallelogram, the coordinates of the mid-point of the AC = Coordinates of the mid-point of the BD
We know, midpoint formula that if P is mid point of A(x₁, y₁) and B(x₂, y₂)

Coordinates of mid-point of AC

= (2, 1)
Coordinates of mid-point of BD

= (2, 1)
Hence, ABCD is a parallelogram.

Q.26. If the points P(a, – 11), Q(5, b), R(2, 15) and S(1, 1) are the vertices of a parallelogram PQRS, find the values of a and b.

We know that the diagonals of a parallelogram bisect each other
So the coordinates of the mid – point of the PR = Coordinates of the mid – point of the QS
{(2 + a)/2,(15 – 11)/2} = {(5 + 1)/2,(b + 1)/2}
2 + a = 6
a = 4
15 – 11 = b + 1
4 = b + 1
b = 3
Hence, a = 4, b = 3

Q.27. If three consecutive vertices of a parallelogram ABCD are A(1, – 2), B(3, 6) and C(5, 10), find its fourth vertex D.

Coordinate of mid – point of AC = {(1 + 5)/2,(– 2 + 10)/2}
implies (3,4)
This is equal to the coordinates of mid – point of BD
3 = (3 + x)/2
6 = 3 + x
x = 3
4 = (6 + y)/2
8 = (6 + y)
y = 2
Hence, D(3, 2)

Q.28. In what ratio does y – axis divide the line segment joining the points (– 4, 7) and (3, – 7)?

Let the coordinate of the point on y axis be (0,y)
0 = (m₁x₂ + m₂x₁)/ m₁ + m₂
0 = (m₁3 + m₂(– 4))/ m₁ + m₂
0 = (3m₁ – 4m₂)/ m₁ + m₂
(3m₁ – 4m₂) = 0
3m₁ = 4m₂
m_1: m₂ = 4:3

Q.29. If the point 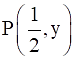 lies on the line segment joining the points A(3, – 5) and B(– 7, 9) then find the ratio in which P divides AB. Also, find the value of y.

Given: The points P(1/2, y) lies on the line AB.
Then,
1/2 = (m₁x₂ + m₂x₁)/ m₁ + m₂
1/2 = (m₁(– 7) + m₂3)/ m₁ + m₂
1/2 = (– 7m₁ + 3m₂)/ m₁ + m₂
(m₁ + m₂) = – 14 m₁ + 6 m₂
15m₁ = 5m₂
m₁: m₂ = 3:5
y = (m₁y₂ + m₂y₁)/ m₁ + m₂
y = (3 × 9 + 5x (– 5))/3 + 5
y = (27 – 25)/8
y = 2/8
y = 1/4

Q.30. Find the ratio in which the line segment joining the points A(3, – 3) and B(– 2, 7) is divided by x – axis. Also, find the point of division.

Let the coordinate of the point on x axis be (x, 0)
0 = (m₁y₂ + m₂y₁)/ m₁ + m₂
0 = (m₁7 + m₂(– 3)/ m₁ + m₂
0 = (7m₁ – 3m₂)/ m₁ + m₂
7m₁ – 3m₂ = 0
7 m₁ = 3m₂
m₁ : m₂ = 3:7
x = (m₁x₂ + m₂x₁)/ m₁ + m₂
x = (3 x(– 2) + 7 × 3)/ 10
× = (– 6 + 21)/ 10
x = 15/10
x = 3/2
Hence the coordinate of the point be (3/2, 0)

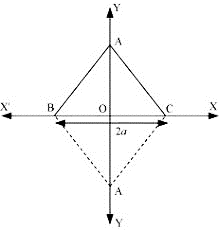
Q.31. The base QR of an equilateral triangle PQR lies on x – axis. The coordinates of the point Q are (– 4, 0) and origin is the midpoint of the base. Find the coordinates of the points P and R.

Let QR be the base
Since origin is mid – point O(0,0) of QR
Then the coordinates of R(x, y) is given by
(– 4 + x)/2 = 0
x = 4
(0 + y)/2 = 0
y = 0
R(4, 0)
Distance of QR = √(4 + 4)² + 0
QR = 8
∴ PR = 8
Let P(x, y)
8 = √(4 – x)² + (0 – y)²
64 = 16 + x² – 8x + y²
Since it will lie on x axis
∴ × = 0
64 = 16 + y²
48 = y²
y = 4√3 or – 4√3
Hence,
P(0, 4√3) or P(0, – 4√3) and R(4, 0)

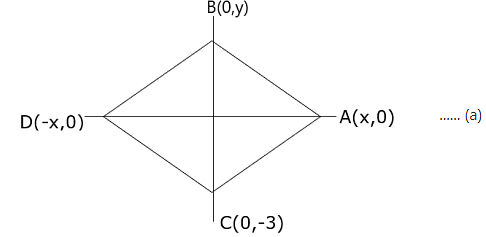
Q.32. The base BC of an equilateral triangle ABC lies on y-axis. The coordinates of point C are (0, –3). The origin is the midpoint of the base. Find the coordinates of the points A and B. Also, find the coordinates of another point D such that ABCD is a rhombus.

The base (BC) of the equilateral triangle ABC lies on y - axis, where, C has the coordinates: (0, - 3).The origin is the midpoint of the base.
The coordinates of the points A and B. Also, the coordinates of another point D such that ABCD is a rhombus.
Now, Δ ABC is an equilateral triangle
∴ AB = AC = BC …(1)
By symmetry the coordinate A lies on x axis.
Also D is another point such that ABCD is rhombus and every side of rhombus is equal to each other.
So For this condition to be possible D will also lie on x axis.
Now,
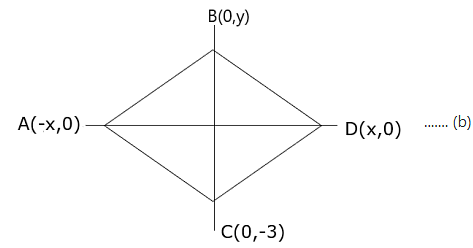
Let coordinates of A be (x,0),B be (0,y) and D be ( -x,0).
or coordinates of A be ( - x,0),B be (0,y) and D be (x,0).
The figures are shown below:


From figure (a)
BC = √(0 - 0)² + ( - 3 - y)²
⇒ BC = √0 + 9 + y² + 6y
⇒ BC = √9 + y² + 6y
Now, AC = √(0 - x)² + ( - 3 - 0)²
⇒ AC = √x² + ( - 3)²
⇒ AC = √(x² + 9)
And
AB = √(0 - x)² + (y - 0)²
⇒ AB = √x² + y²
From (1)
AB = AC
⇒ √x² + y² = √x² + 9
Taking square on both sides we get,
x² + y² = x² + 9
⇒ y² = 9
⇒ y = ± 3
Since B lies in positive y direction.
∴ The coordinates of B are (0,3)
Now from (1) AB = BC
⇒√ x² + y² = √9 + y² + 6y
Take square on both sides
⇒ x² + y² = 9 + y² + 6y
⇒ x² = 9 + 6y
Put the value of y to get,
⇒ x² = 9 + 6(3)
⇒ x² = 9 + 18
⇒ x² = 27
⇒ x = ± 3√3
Hence the coordinates of A can be ( 3√3,0) or ( - 3√3,0)
Also, ABCD is a rhombus.
⇒ AB = BC = DC = BD
So coordinates of D will be ( -3√3,0) or ( 3√3,0)
Hence coordinates are A( 3√3,0) , B(0,3) , D( - 3√3,0)
Or coordinates are A( -3√3,0) , B(0,3) , D( 3√3,0)

Q.33. Find the ratio in which the point P(– 1, y) lying on the line segment joining points A(– 3, 10) and B(6, – 8) divides it. Also, find the value of y.

– 1 = (m₁x₂ + m₂x₁)/ m₁ + m₂
– 1 = (m16 + m₂(– 3))/ m₁ + m₂
– 1 = (6m₁ – 3m₂)/ m₁ + m₂
(6m₁ – 3m₂) = – m₁ – m₂
7m₁ = 2 m₂
m₁: m₂ = 2:7
y = (m₁y₂ + m₂y₁)/ m₁ + m₂
= (2x(– 8) + 7 × 10)/9
= (– 16 + 70)/9
= 54 / 9
y = 6

Q.34. ABCD is a rectangle formed by the points A(– 1, – 1), B(– 1, 4), C(5, 4) and D(5, – 1). If P, Q, R and S be the midpoints of AB, BC, CD, and DA respectively, show that PQRS is a rhombus.

The figure is shown below:

P(x, y) = (– 1 – 1)/2 , (4 – 1)/2
= (– 1,3/2)
Q(x, y) = (5 – 1)/2 , (4 + 4)/2
= (2, 4)
R(x, y) = (5 + 5)/2 , (– 1 + 4)/2
= (5, 3/2)
S(x, y) = (5 – 1)/2 , (– 1 – 1)/2
= (2, – 1)
Coordinates of mid – point of PR = Coordinates of mid – point of QS
Coordinates of mid – point of PR = {(5 – 1)/2 ,(3/2 + 3/2)/2} = (2,3/2)
Coordinates of mid – point of QS = {(2 + 2)/2 , (– 1 + 4)/2 = (2,3/2)
Hence PQRS is a Rhombus.

Q.35. The midpoint P of the line segment joining the points A(– 10, 4) and B(– 2, 0) lies on the line segment joining the points C(– 9, – 4) and D(– 4, y). Find the ratio in which P divides CD. Also, find the value of y.

For P(x, y)
X = (– 10 – 2)/2 = – 6
Y = (4 + 0)/2 = 2
Thus, P(– 6, 2)
Now
– 6 = (m₁x₂ + m₂x₁)/ m₁ + m₂
– 6 = (m₁(– 4) + m₂(– 9))/ m₁ + m₂
– 6 = (– 4m₁ – 9m₂)/ m₁ + m₂
– 6(m₁ + m₂) = – 4 m₁ – 9 m₂
– 2m₁ = – 3m₂
m₁:m₂ = 3:2,
2 = (m₁y₂ + m₂y₁)/ m₁ + m₂
2 = (3 × y + 2x (– 4))/5
2 = (3y – 8)/5
10 = 3y – 8
3y = 18
y = 6

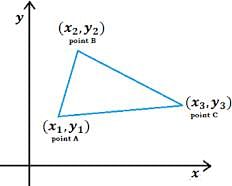
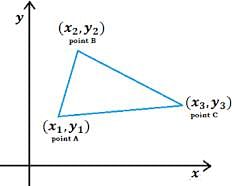
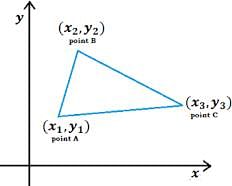
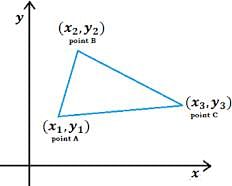
Q.1. Find the area of ΔABC whose vertices are:
A(1, 2), B(–2, 3) and C(–3, –4)

Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(1(–2 + 3)–2(–4–2)–3(2–3))
= 1/2(1 + 12 + 3)
= 8 sq units

Q.2. Find the area of ΔABC whose vertices are:
A(–5, 7), B(–4, –5) and C(4, 5)

Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(–5(–5–5)–4(5–7) + 4(7 + 5))
= 1/2(–50 + 8 + 48)
= 5 sq units

Q.3. Find the area of ΔABC whose vertices are:
A(3, 8), B(–4, 2) and C(5, –1)

Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(3(2 + 1)–4(–1–8) + 5(8–2))
= 1/2(9 + 36 + 30)
= 1/2(75)
= 37.5 sq units

Q.4. Find the area of ΔABC whose vertices are:
A(10, –6), B(2, 5) and C(–1, 3)

Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(10(5–3) + 2(3 + 6)–1(–6–5))
= 1/2(20 + 18 + 11)
= 1/2(49)
= 24.5 sq units

Q.5. Find the area of quadrilateral ABCD whose vertices are A(3, –1), B(9, –5), C(14, 0) and D(9, 19).

For triangle ABC
Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(3(–5–0) + 9(0 + 1) + 14(–1 + 5))
= 1/2(–15 + 9 + 56)
= 1/2(50)
= 25
For triangle ACD
Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(3(0–19) + 14(19 + 1) + 9(–1–0))
= 1/2(–57 + 280–9)
= 1/2(214)
= 107
Area of ABCD = Area of ABC + Area of ACD
= 25 + 107
= 132 sq units

Q.6. Find the area of quadrilateral PQRS whose vertices are P(–5, –3), Q(–4, – 6), R(2, –3) and S(1, 2).

For triangle PQR
Area of triangle
= l1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))l
= 1/2(–5(–6 + 3)–4(–3 + 3) + 2(–3 + 6))
= 1/2(15 + 0 + 6)
= 1/2(21)
For triangle PRS
Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(–5(–3–2) + 2(2–(–3)) + 1(–3 + 3))
= 1/2(25 + 10 + 0)
= 1/2(35)
Area of ABCD = Area of ABC + Area of ACD
= 21/2 + 35/ 2
= 28 sq units

Q.7. Find the area of quadrilateral ABCD whose vertices are A(–3, –1), B(–2, – 4), C(4, –1) and D(3, 4).

We divide quadrilateral in two triangles, such that
Area of ABCD = Area of ΔABC + Area of ΔACD

Also,
We know area of a triangle, if it’s coordinates are A(x­₁, y₁), B(x₂, y₂) and C(x₃, y₃) is

Therefore,
Area of ABC
= |1/2[-3(-1+4)-2(-1+1)+4(-1+4)]
= |1/2(-9-12)|
= 21/2
Area of ACD

Area of ABCD = Area of ABC + Area of ACD
= (21/2)+(35/2)
= 56/2
= 28 sq units.

Q.8. Find the area of quadrilateral ABCD whose vertices are A(–5, 7), B(–4, –5), C(–1, – 6) and D(4, 5).

For triangle ABC
Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(–5(–5 + 6)–4(–6–7)–1(7 + 5))
= 1/2(–5 + 52–12)
= 1/2(35)
For triangle ACD
Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(–5(–6–5)–1(5–7) + 4(7 + 6))
= 1/2(–55 + 2 + 52)
= 1/2(1)
Area of ABCD = Area of ABC + Area of ACD
= 18 sq units

Q.9. Find the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).

By applying section formula we get the coordinates of mid points of AB,BC and AC.
Mid point of AB = P = {(2 + 4)/2,(1 + 3)/2}
P = (3,2)
Mid point of BC = Q = {(4 + 2)/2,(3 + 5)/2}
Q = (3,4)
Mid point of AC = R = {(2 + 2)/2,(1 + 5)/2}
R = (2,3)
For triangle PQR
Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(3(4–3) + 3(3–2) + 2(2–4))
= 1/2(3 + 3–4)
= 1/2(2)
= 1 sq unit

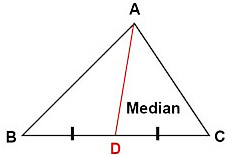
Q.10. A(7, –3), B(5, 3) and C(3, –1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.

D = {(3 + 5)/2,(3–1)/2} = (4,1)
For triangle ABD
Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(7(3–1) + 5(1 + 3) + 4(–3–3))
= 1/2(14 + 20–24)
= 1/2(10)
= 5 sq unit
For triangle ACD
Area of triangle
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(7(–1–1) + 3(1 + 3) + 4(–3 + 1))
= 1/2(–14 + 12–8)
= 1/2(10)
= 5 sq unit
Hence area of triangle ABD and ACD is equal.

Q.11. Find the area of ΔABC with A(1, –4) and midpoints of sides through A being (2, –1) and (0, –1).

The diagram is given below:

Coordinates of B
2 = (1 + x)/2 [by section formula]
4 = 1 + x
X = 3
–1 = (–4 + y)/2
–2 = (–4 + y)
Y = 2
∴ the coordinates of B(3, 2)
Coordinates of C [by section formula]
0 = (1 + x)/2
0 = (1 + x)
x = –1
–1 = (–4 + y)/2
–2 = (–4 + y)
Y = 2
∴ the coordinates of point C are (–1,2)
Now, Area of triangle ABC
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(1(2–2) + 3(2 + 4)–1(–4–2))
= 1/2(0 + 18 + 6)
= 1/2(24)
= 12 sq unit

Q.12. A(6, 1), B(8, 2) and C(9, 4) are the vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ΔADE.

Let (x, y) be the coordinates of D and ( x’, y' ) be the coordinates of E. since the diagonals of a parallelogram bisect each other at the same point, therefore
(x + 8)/2 = (6 + 9)/2
X = 7
(y + 2)/2 = (1 + 4)/2
Y = 3
Thus, the coordinates of D are (7,3)
E is the midpoint of DC,
therefore
x’ = (7 + 9)/2 = 8
y’ = (3 + 4)/2 = 7/2
Thus, the coordinates of E are ( 8,7/ 2)
Let A(x₁,y₁) = A(6,1), E(x₂,y₂) = (8,7/2) and D(x₃,y₃) = D(7,3)
Now Area
= 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
= 1/2(6(7/2–3) + 8(3–1) + 7(1–7/2))
= 1/2(3/2)
= 3/4 sq unit
Hence, the area of the triangle ΔADE is 3/4 sq. units.

Q.13. If the vertices of ΔABC be A(1, –3), B(4, p) and C(–9, 7) and its area is 15 square units, find the values of p.

Area = 15
⇒ Δ = 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
15 = 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
15 = 1/2(1(p–7) + 4(7 + 3)–9(–3–p))
15 = 1/2(10p + 16)
|10p + 16| = 30
10p + 16 = 30 or –30
Hence, p = −9 or p = −3.

Q.14. Find the value of k so that the area of the triangle with verticesn5 rticles1 A(k + 1,1), B(4, –3) and C(7, –k) is 6 square units.

Δ = 6
⇒ Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
6 = 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
6 = 1/2(k + 1(–3 + k) + 4(–k–1) + 7(1 + 3))
6 = 1/2(k²–2k–3–4k–4 + 28)
k² – 6k + 9 = 0
k = 3

Q.15. For what value of k(k > 0) is the area of the triangle with vertices (–2,5) and (k, –4) and (2k + 1,10) equal to 53 square units?

Given the area of triangle, Δ = 53
⇒ Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
53 = 1/2{–2(–4–10) + k(10–5) + 2k + 1(5 + 4)}
53 = 1/2{28 + 5k + 9(2k + 1)}
106 = (28 + 5k + 18k + 9)
37 + 3k = 106
23k = 69
k = 3

Q.16. Show that the following points are collinear:
A(2, – 2), B(–3, 8) and C(–1, 4)

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Given, the area of the triangle, Δ = 0
⇒ Δ = 1/2(x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂))
⇒ Δ = 1/2{2 (8– 4) + (–3) (4 + 2) –1 (2– 8)}
⇒ Δ = 1/2 {8–18 + 10}
⇒ Δ = 0
Hence the points A(2, – 2), B(–3, 8) and C(–1, 4) are collinear.

Q.17. Show that the following points are collinear:
A(–5, 1), B(5, 5) and C(10, 7)

To show that the points are collinear, we show that the area of triangle is equilateral = 0
⇒ Δ = 1/2 {(x₁(y₂−y₃) + x₂₍y₃−y₁) + x₃(y₁−y₂))}
⇒ Δ = 1/2{–5(5– 7) + 5 (7–1) + 10 (1–5) }
⇒ Δ = 1/2{10 + 30–40}
⇒ Δ = 0
Hence collinear.

Q.18. Show that the following points are collinear:
A(5, 1), B(1, –1) and C(11, 4)

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
⇒ Δ = 1/2{5(–1– 4) + 1 (4– 1) + 11 (1 + 1)}
⇒ 1/2{–25 + 3 + 22}
= 0
Hence collinear.

Q.19. Show that the following points are collinear:

A(8, 1), B(3, –4) and C(2, –5)
To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
⇒ 1/2{8(–4 + 5) + 3 (–5–1) + 2 (1 + 4)}
⇒ 1/2{8–18 + 10}
= 0
Hence collinear.

Q.20. Find the value of x for which the points A(x, 2), B(–3, –4) and C(7, –5) are collinear.

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2 {x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
⇒ Δ = 1/2{x(–4 + 5)–3 (–5– 2) + 7 (2 + 4)} = 0
⇒ Δ = 1/2{x + 21 + 42} = 0
x = –63

Q.21. For what value of x are the points A(–3, 12), B(7, 6) and C(x, 9) collinear?

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
⇒ Δ = 1/2{–3(6–9) + 7 (9 – 12) + x(12– 6)} = 0
⇒ (–3)(–3) + 7(–3) + 6x = 0
⇒ 9–21 + 6x = 0
6x = 12
x = 2

Q.22. For what value of y are the points P(1, 4), Q(3, y) and R(–3, 16) are collinear?

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
⇒ Δ = 1/2{1(y–16) + 3 (16–4)–3 (4–y)} = 0
⇒ y–16 + 36–12 + 3y = 0
⇒ 8 + 4y = 0
⇒ 4y = –8
y = –2

Q.23. Find the value of y for which the points A(–3, 9), B(2, y) and C(4, –5) are collinear.

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2{x₁(y₂−y₃) + x₂₍y₃−y₁) + x₃(y₁−y₂)}
⇒ Δ = 1/2{–3(y + 5) + 2 (–5–9) + 4 (9–y)} = 0
⇒ –3y–15–28 + 36–4y = 0
⇒ 7y = 36–43
y = –1

Q.24. For what values of k are the points A(8, 1), B( 3, –2k) and C(k, –5) collinear.

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
⇒ Δ = 1/2{8(–2k + 5) + 3 (–5–1) + k (1 + 2k)} = 0
⇒ –16k + 40–18 + k + 2k2 = 0
⇒ 2k² + 15k + 22 = 0
⇒ 2k²–11k–14k + 22 = 0
⇒ K(2k–11)–2(2k–11) = 0
k = 2 or k = 11/2

Q.25. Find a relation between x and y, if the points A(2, 1), B(x, y) and C(7, 5) are collinear.

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
⇒ Δ = 1/2{2(y–5) + x (5– 1) + 7 (1– y)}
⇒ 2y–10 + 4x–7–7y = 0
⇒ 4x –5y – 3 = 0

Q.26. Find a relation between x and y, if the points A(x, y), B(–5, 7) and C(–4, 5) are collinear.

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
⇒ Δ = 1/2{x (7–5) + (–5) (–5–y) –4 (y– 7)}
⇒ 7x–5x–25 + 5y–4y + 28 = 0
⇒ 2x + y + 3 = 0

Q.27. Prove that the points A(a, 0), B(0, b) and C(1, 1) are collinear, if

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)} = 0
⇒ Δ = 1/2{a(b– 1) + 0 (1– 0) + 1 (0– b)} = 0
⇒ (ab–a–b) = 0
Dividing the equation by ab.
1–1/b–1/a
1–(1/a + 1/b)
1–1 = 0
Hence collinear.

Q.28. If the points P(–3, 9), Q(a, b) and R(4, –5) are collinear and a + b = 1, find the values of a and b.

To show that the points are collinear, we show that the area of triangle is equilateral = 0
Δ = 0
Δ = 1/2{x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)}
⇒ Δ = 1/2{–3 (b + 5) + a (–5–9) + 4 (9–b)} = 0
⇒ –3b–150–14a + 36–4b = 0
2a + b = 3
Now solving a + b =1 and 2a + b = 3 we get a = 2 and b = −1.
Hence a = 2, b = –1