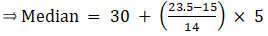RS Aggarwal Solutions: Mean, Median, Mode of Grouped Data, Cumulative Frequency Graph and Ogive- 2 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
| Table of contents |

|
| Exercise: 9c |

|
| Exercise: 9d |

|
| Exercise: 9e |

|
| Formative Assessment (unit Test) |

|
Exercise: 9c
Q.1. Find the mode of the following frequency distribution:
Here, the maximum class frequency is 45.
The class corresponding to this frequency is the modal class. ⇒ modal class = 30 - 40
∴ lower limit of the modal class (l) = 30
Modal class size (h) = 10
Frequency of the modal class (f1) = 45
Frequency of class preceding the modal class (f0) = 35
Frequency of class succeeding the modal (f2) = 25
Mode is given by,
⇒ Mode = 30 + 3.33 = 33.33
Hence, the mode is 33.33.
Q.2. Compute the mode of the following data:
Here, the maximum class frequency is 28.
The class corresponding to this frequency is the modal class. ⇒ modal class = 40 - 60
∴ lower limit of the modal class (l) = 40
Modal class size (h) = 20
Frequency of the modal class (f1) = 28
Frequency of class preceding the modal class (f0) = 16
Frequency of class succeeding the modal (f2) = 20
Mode is given by,
⇒ Mode = 40 + 12 = 52
Hence, the mode is 52.
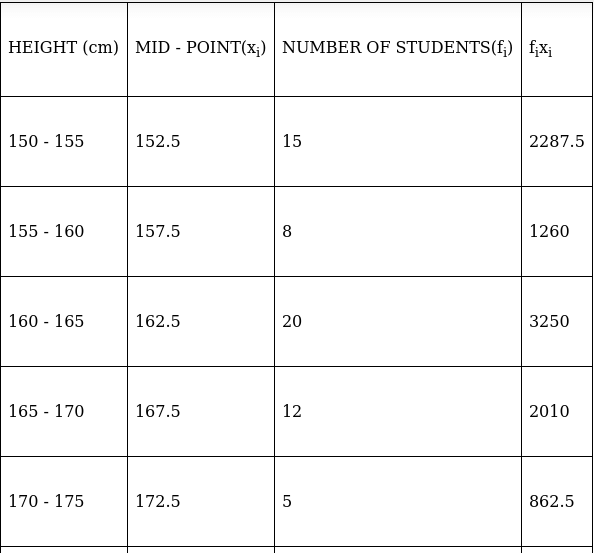
Q.3. Heights of students of Class X are given in the following frequency distribution: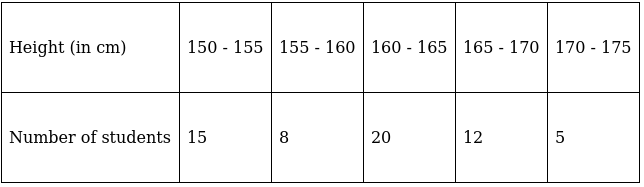
Find the modal height.
Also, find the mean height. Compare and interpret the two measures of central tendency.
Here, the maximum class frequency is 20.
The class corresponding to this frequency is the modal class. ⇒ modal class = 160 - 165
∴ lower limit of the modal class (l) = 160
Modal class size (h) = 5
Frequency of the modal class (f1) = 20
Frequency of class preceding the modal class (f0) = 8
Frequency of class succeeding the modal (f2) = 12
Mode is given by,
⇒ Mode = 160 + 3 = 163
Hence, the mode is 163 cm.
Mode represents frequency, hence 163 cm is the height of maximum number of students.
To find the mean, we will solve by using direct method.
We have got
Σfi = 60 & Σfixi = 9670
∵ mean is given by= 161.17
Thus, mean is 161.17
Mean represents average, thus 161.7 cm is the average height of all the students.
Q.4. Find the mode of the following distribution: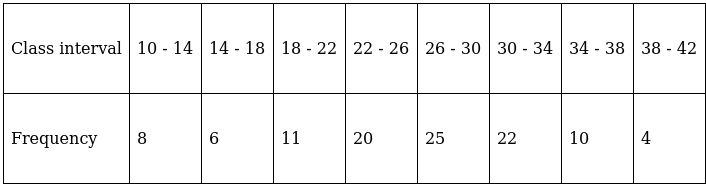
Here, the maximum class frequency is 25.
The class corresponding to this frequency is the modal class. ⇒ modal class = 26 - 30
∴ lower limit of the modal class (l) = 26
Modal class size (h) = 4
Frequency of the modal class (f1) = 25
Frequency of class preceding the modal class (f0) = 20
Frequency of class succeeding the modal (f2) = 22
Mode is given by,
⇒ Mode = 26 + 2.5 = 28.5
Hence, the mode is 28.5.
Q.5. Given below is the distribution of Total household expenditure of 200 manual workers in a city.

Find the expenditure done by maximum number of manual workers.
Expenditure done by maximum number of manual workers is estimated by finding mode.
So here, the maximum class frequency is 40.
The class corresponding to this frequency is the modal class. ⇒ modal class = 1500 - 2000
∴ lower limit of the modal class (l) = 1500
Modal class size (h) = 500
Frequency of the modal class (f1) = 40
Frequency of class preceding the modal class (f0) = 24
Frequency of class succeeding the modal (f2) = 31
Mode is given by,
⇒ Mode = 1500 + 320 = 1820
Hence, the mode is Rs.1820.
Q.6. Calculate the mode from the following data: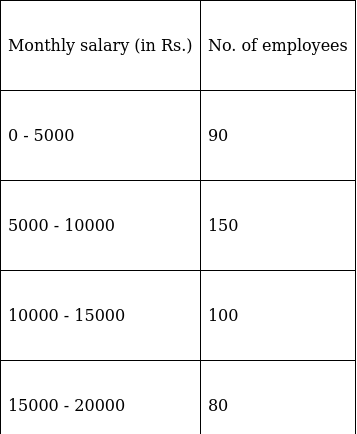

Here, the maximum class frequency is 150.
The class corresponding to this frequency is the modal class. ⇒ modal class = 5000 - 10000
∴ lower limit of the modal class (l) = 5000
Modal class size (h) = 5000
Frequency of the modal class (f1) = 150
Frequency of class preceding the modal class (f0) = 90
Frequency of class succeeding the modal (f2) = 100
Mode is given by,
⇒ Mode = 5000 + 2727.27 = 7727.27
Hence, the mode is Rs.7727.27.
Q.7. Compute the mode from the following data: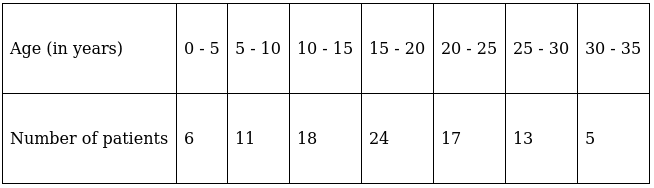
Here, the maximum class frequency is 24.
The class corresponding to this frequency is the modal class. ⇒ modal class = 15 - 20
∴ lower limit of the modal class (l) = 15
Modal class size (h) = 5
Frequency of the modal class (f1) = 24
Frequency of class preceding the modal class (f0) = 18
Frequency of class succeeding the modal (f2) = 17
Mode is given by,
⇒ Mode = 15 + 2.30 = 17.30
Hence, the mode is 17.30 years.
Q.8. Compute the mode from the following series:
Here, the maximum class frequency is 32.
The class corresponding to this frequency is the modal class. ⇒ modal class = 85 - 95
∴ lower limit of the modal class (l) = 85
Modal class size (h) = 10
Frequency of the modal class (f1) = 32
Frequency of class preceding the modal class (f0) = 30
Frequency of class succeeding the modal (f2) = 6
Mode is given by,
⇒ Mode = 85 + 0.71 = 85.71
Hence, the mode is 85.71.
Q.9. Compute the mode of the following data:
Since, the given data is in inclusive series, it needs to get converted in exclusive series.
Here, the maximum class frequency is 28.
The class corresponding to this frequency is the modal class. ⇒ modal class = 15.5 - 20.5
∴ lower limit of the modal class (l) = 15.5
Modal class size (h) = 5
Frequency of the modal class (f1) = 28
Frequency of class preceding the modal class (f0) = 18
Frequency of class succeeding the modal (f2) = 20
Mode is given by,
⇒ Mode = 15.5 + 2.78 = 23.28
Hence, the mode is 23.28.
Q.10. The age wise participation of students in the Annual Function of a school is shown in the following distribution.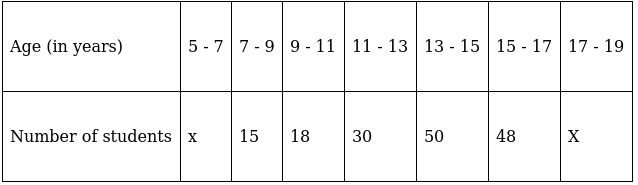
Find the missing frequencies when the Sum of frequencies is 181. Also, find the mode of the data.
To find frequencies, we have Sum of frequencies that is, 181.
Using Sum of frequencies = 181,
x + 15 + 18 + 30 + 50 + 48 + x = 181
⇒ 2x + 161 = 181
⇒ 2x = 181 – 161 = 20
⇒ x = 10
Thus we have,
Here, the maximum class frequency is 50.
The class corresponding to this frequency is the modal class. ⇒ modal class = 13 - 15
∴ lower limit of the modal class (l) = 13
Modal class size (h) = 2
Frequency of the modal class (f1) = 50
Frequency of class preceding the modal class (f0) = 30
Frequency of class succeeding the modal (f2) = 48
Mode is given by,
⇒ Mode = 13 + 1.82 = 14.82
Hence, the mode is 14.82.
Exercise: 9d
Q.1. Find the mean, mode and median of the following frequency distribution: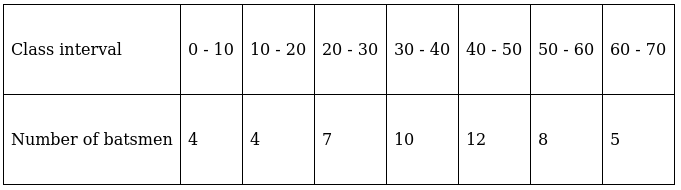
To find mean, we will solve by direct method:
We have got
Σfi = 50 & Σfixi = 1910
∵ mean is given by= 38.2
To find median,
Assume Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
So, N = 50
⇒ N/2 = 50/2 = 25
The cumulative frequency just greater than (N/2 = ) 25 is 37, so the corresponding median class is 40 - 50 and accordingly we get Cf = 25(cumulative frequency before the median class).
Now, since median class is 40 - 50.
∴ l = 40, h = 10, f = 16, N/2 = 25 and Cf = 25
Median is given by,
= 40 + 0
= 40
And we know that,
Mode = 3(Median) – 2(Mean)
= 3(40) – 2(38.2)
= 120 – 76.4
= 43.6
Hence, mean is 38.2, median is 40 and mode is 43.6.
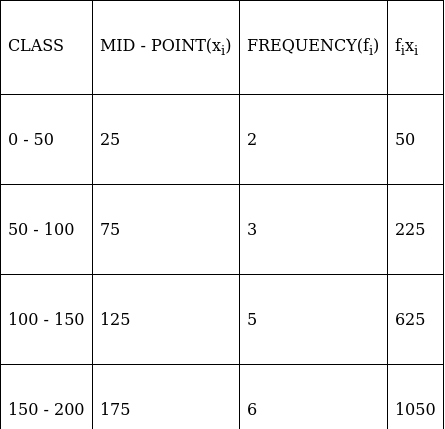
Q.2. Find the mean, median and mode of the following data: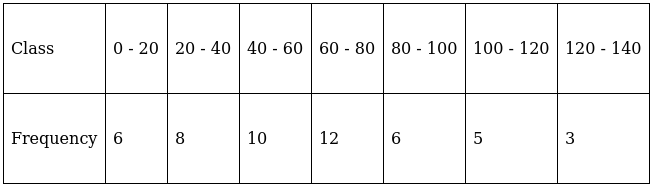
To find mean, we will solve by direct method:
We have got
Σfi = 50 & Σfixi = 3120
∵ mean is given by
To find median,
Assume Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
So, N = 50
⇒ N/2 = 50/2 = 25
The cumulative frequency just greater than (N/2 = ) 25 is 36, so the corresponding median class is 60 - 80 and accordingly we get Cf = 24(cumulative frequency before the median class).
Now, since median class is 60 - 80.
∴ l = 60, h = 20, f = 12, N/2 = 25 and Cf = 24
Median is given by,
= 60 + 1.67
= 61.67
And we know that,
Mode = 3(Median) – 2(Mean)
= 3(61.67) – 2(62.4)
= 185.01 – 124.8
= 60.21
Hence, mean is 62.4, median is 61.67 and mode is 60.21.
Q.3. Find the mean, median and mode of the following data:
To find mean, we will solve by direct method:
We have got
Σfi = 25 & Σfixi = 4171
∵ mean is given by= 169
To find median,
Assume Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
So, N = 25
⇒ N/2 = 25/2 = 12.5
The cumulative frequency just greater than (N/2 = ) 12.5 is 16, so the corresponding median class is 150 - 200 and accordingly we get Cf = 10(cumulative frequency before the median class).
Now, since median class is 150 - 200.
∴ l = 150, h = 50, f = 6, N/2 = 12.5 and Cf = 10
Median is given by,
= 150 + 20.83
= 170.83
And we know that,
Mode = 3(Median) – 2(Mean)
= 3(170.83) – 2(169)
= 512.49 – 338
= 174.49
Hence, mean is 169, median is 170.83 and mode is 174.49.
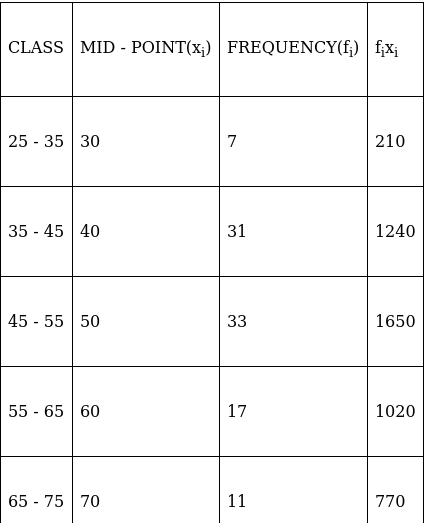
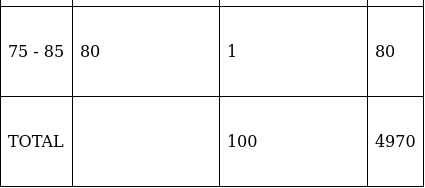
Q.4. Find the mode, median and mean for the following data:
To find mean, we will solve by direct method:
We have got
Σfi = 100 & Σfixi = 4970
∵ mean is given by= 49.7
To find median,
Assume Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
So, N = 100
⇒ N/2 = 100/2 = 50
The cumulative frequency just greater than (N/2 = ) 50 is 71, so the corresponding median class is 45 - 55 and accordingly we get Cf = 38(cumulative frequency before the median class).
Now, since median class is 45 - 55.
∴ l = 45, h = 10, f = 33, N/2 = 50 and Cf = 38
Median is given by,
= 45 + 3.64
= 48.64
And we know that,
Mode = 3(Median) – 2(Mean)
= 3(48.64) – 2(49.7)
= 145.92 – 99.4
= 46.52
Hence, mean is 49.7, median is 48.64 and mode is 46.52.
Q.5. A survey regarding the heights (in cm) of 50 girls of a class was conducted and the following data was obtained: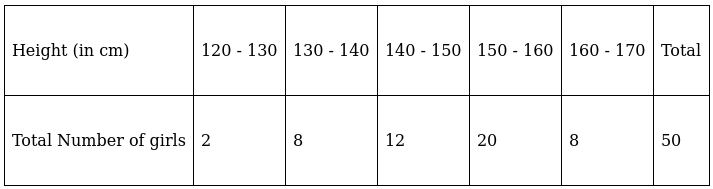
Find the mean, median and mode of the above data.
To find mean, we will solve by direct method:
We have got
Σfi = 50 & Σfixi = 7490
∵ mean is given by= 149.8
To find median,
Assume Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
So, N = 50
⇒ N/2 = 50/2 = 25
The cumulative frequency just greater than (N/2 = ) 25 is 42, so the corresponding median class is 150 - 160 and accordingly we get Cf = 22(cumulative frequency before the median class).
Now, since median class is 150 - 160.
∴ l = 150, h = 10, f = 20, N/2 = 25 and Cf = 22
Median is given by,
= 150 + 1.5
= 151.5
And we know that,
Mode = 3(Median) – 2(Mean)
= 3(151.5) – 2(149.8)
= 454.5 – 299.6
= 154.9
Hence, mean is 149.8, median is 151.5 and mode is 154.9.
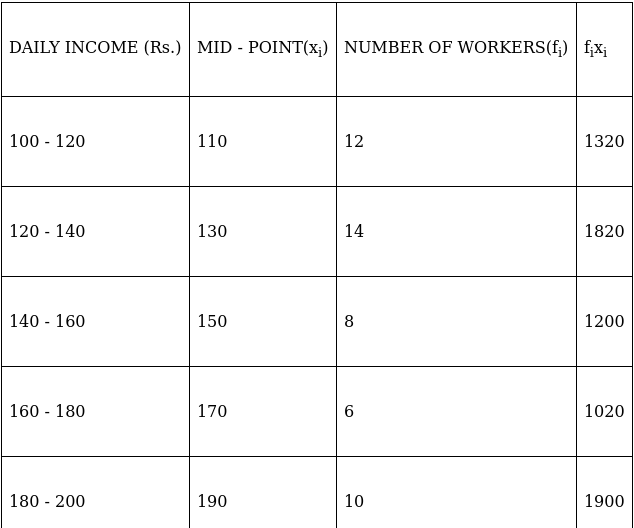
Q.6. The following table gives the daily income of 50 workers of a factory: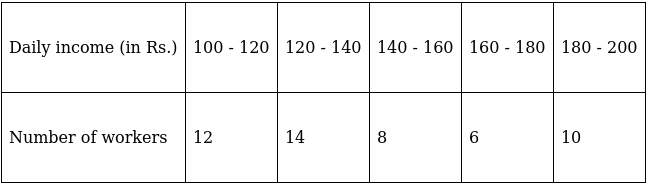
Find the mean, mode and median of the above data.
To find mean, we will solve by direct method:
We have got
Σfi = 50 & Σfixi = 7260
∵ mean is given by= 145.2
To find median,
Assume Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
So, N = 50
⇒ N/2 = 50/2 = 25
The cumulative frequency just greater than (N/2 = ) 25 is 26, so the corresponding median class is 120 - 140 and accordingly we get Cf = 12(cumulative frequency before the median class).
Now, since median class is 120 - 140.
∴ l = 120, h = 20, f = 14, N/2 = 25 and Cf = 12
Median is given by,
= 120 + 18.57
= 138.57
And we know that,
Mode = 3(Median) – 2(Mean)
= 3(138.57) – 2(145.2)
= 415.71 – 290.4
= 125.31
Hence, mean is 145.2, median is 138.57 and mode is 125.31.
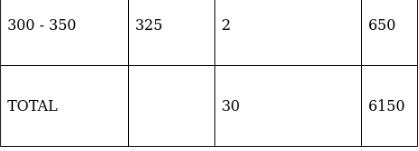
Q.7. The table below shows the daily expenditure on food of 30 households in a locality:
Find the mean and median daily expenditure on food.
To find mean, we will solve by direct method:
We have got
Σfi = 30 & Σfixi = 6150
∵ mean is given by= 205
To find median,
Assume Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
So, N = 30
⇒ N/2 = 30/2 = 15
The cumulative frequency just greater than (N/2 = ) 15 is 25, so the corresponding median class is 200 - 250 and accordingly we get Cf = 13(cumulative frequency before the median class).
Now, since median class is 200 - 250.
∴ l = 200, h = 50, f = 12, N/2 = 15 and Cf = 13
Median is given by,
= 200 + 8.33 = 208.33
Hence, mean is 205 and median is 208.33.
Exercise: 9e
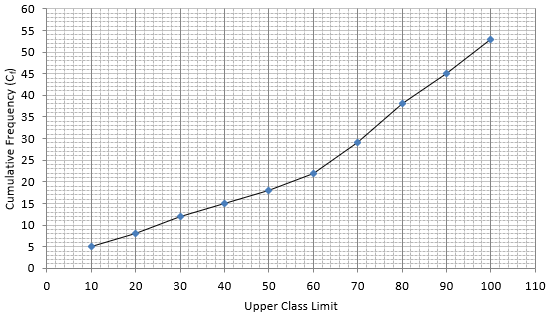
Q.1. Find the median of the following data by making a 'less than ogive'.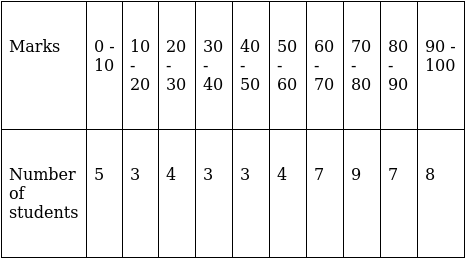
The frequency distribution table for ‘less than’ type is:
Lets plot a graph of ‘less than ogive’, taking upper limits of the class intervals on x - axis and cumulative frequencies on y - axis.
As we have N = 53 by the frequency table.
N/2 = 53/2 = 26.5
Mark 26.5 on y - axis and the corresponding point on x - axis would be the median.
The corresponding point on x - axis is 66.4.
Hence, median is 66.4.
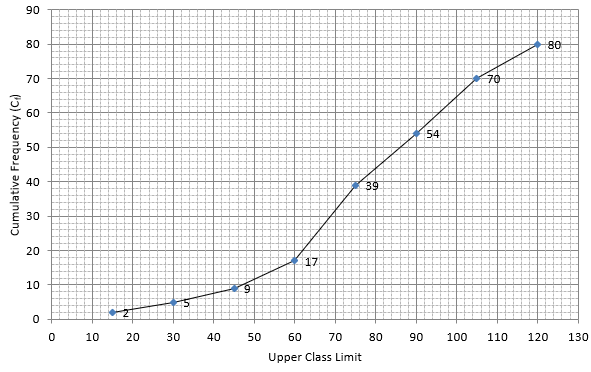
Q.2. The given distribution shows the number of wickets taken by the bowlers in one - day international cricket matches:
Draw a 'less than type' ogive from the above data. Find the median.
Lets plot a graph of ‘less than ogive’, taking upper limits of the class intervals on x - axis and cumulative frequencies on y - axis.
As we have N = 80 by the frequency table.
N/2 = 80/2 = 40
Mark 40 on y - axis and the corresponding point on x - axis would be the median.
The corresponding point on x - axis is 76.
Hence, median is 76.
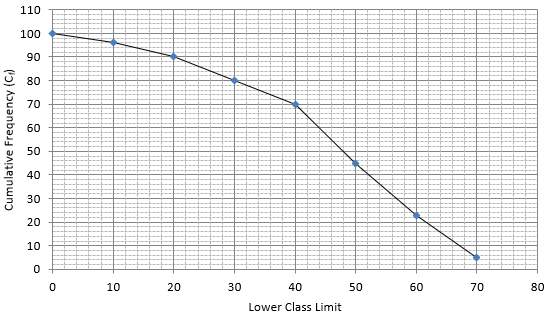
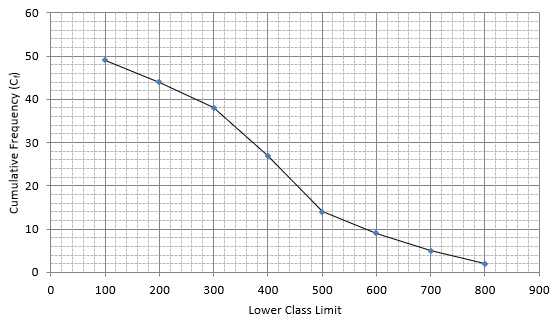
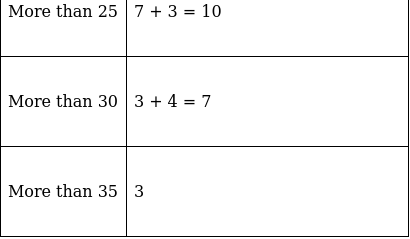
Q.3. Draw a 'more than' ogive for the data given below which gives the marks of 100 students.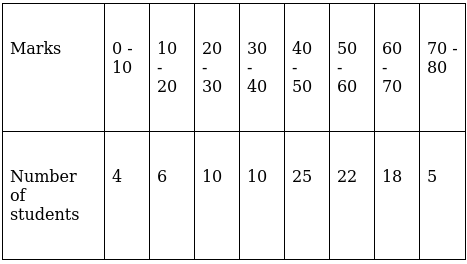
The frequency distribution table for ‘more than’ type is:
Lets plot a graph of ‘more than’ ogive, taking lower limits of the class intervals on x - axis and cumulative frequencies on y - axis.
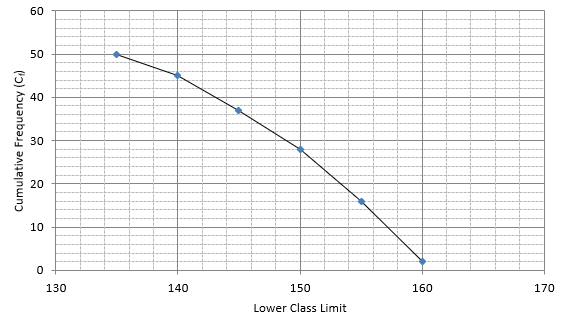
Q.4. The heights of 50 girls of Class X of a school are recorded as follows: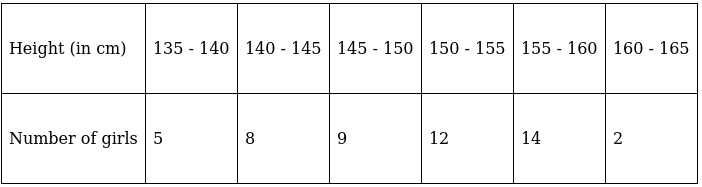
Draw a 'more than type' ogive for the above data.
The frequency distribution table for ‘more than’ type is:
Lets plot a graph of ‘more than’ ogive, taking lower limits of the class intervals on x - axis and cumulative frequencies on y - axis.
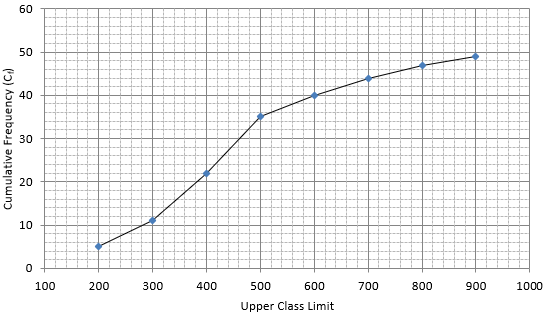
Q.5. The monthly consumption of electricity (in units) of some families of a locality is given in the following frequency distribution:
Prepare a 'more than type' ogive for the given frequency distribution.
The frequency distribution table for ‘more than’ type is:
Lets plot a graph of ‘more than’ ogive, taking lower limits of the class intervals on x - axis and cumulative frequencies on y - axis.
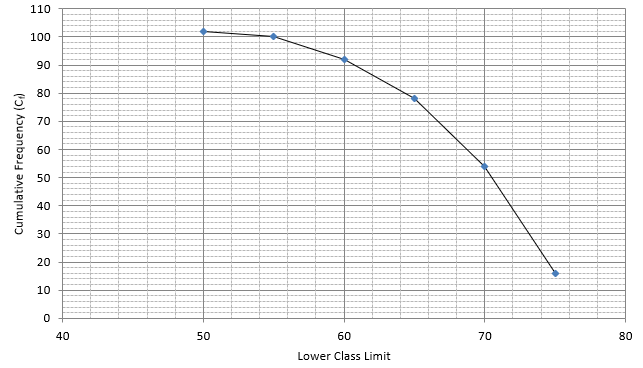
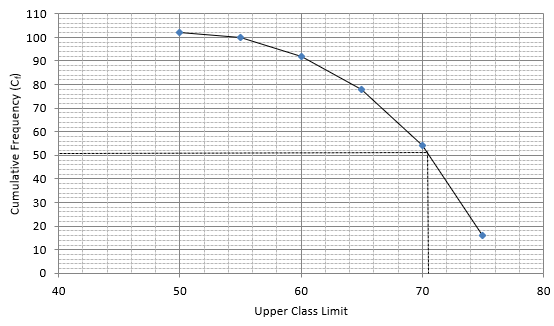
Q.6. The following table gives the production yield per hectare of wheat of 100 farms of a village.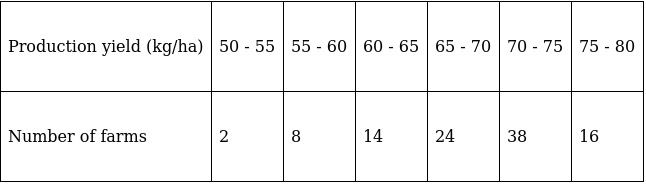
Change the distribution to a 'more than type' distribution and draw its ogive. Using ogive, find the median of the given data.
The frequency distribution table for ‘more than’ type is:
Lets plot a graph of ‘more than’ ogive, taking lower limits of the class intervals on x - axis and cumulative frequencies on y - axis.
As we have N = 102 by the frequency table.
N/2 = 102/2 = 51
Mark 51 on y - axis and the corresponding point on x - axis would be the median.
The corresponding point on x - axis is 70.5.
Hence, median is 70.5.
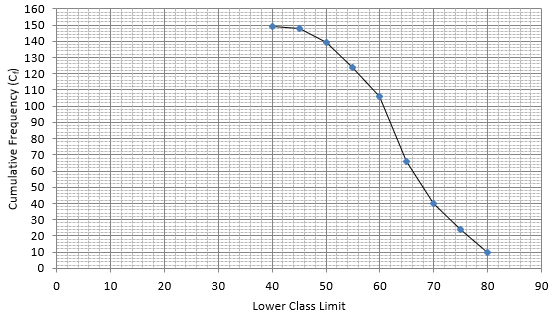
Q.7. The table given below shows the weekly expenditures on food of some households in a locality.

Draw a 'less than type ogive' and a 'more than type ogive' for this distribution.
The frequency distribution table for ‘less than’ type is:
Lets plot the graph of ‘less than ogive’, taking upper limits of the class intervals on x - axis and cumulative frequencies on y - axis.The frequency distribution table for ‘more than’ type is:
Lets plot a graph of ‘more than’ ogive, taking lower limits of the class intervals on x - axis and cumulative frequencies on y - axis.
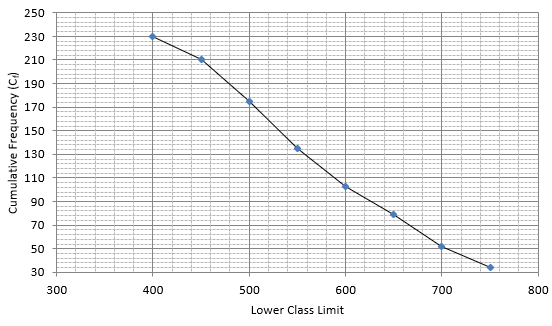
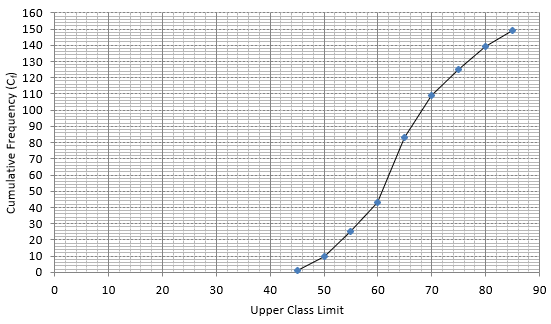
Q.8. From the following frequency distribution, prepare the 'more than' ogive.

Also, find the median.
The frequency distribution table for ‘more than’ type is:
Lets plot a graph of ‘more than’ ogive, taking lower limits of the class intervals on x - axis and cumulative frequencies on y - axis.
As we have N = 230 by the frequency table.
N/2 = 230/2 = 115
Mark 115 on y - axis and the corresponding point on x - axis would be the median.
.................The corresponding point on x - axis is 590.
Hence, median is 590.
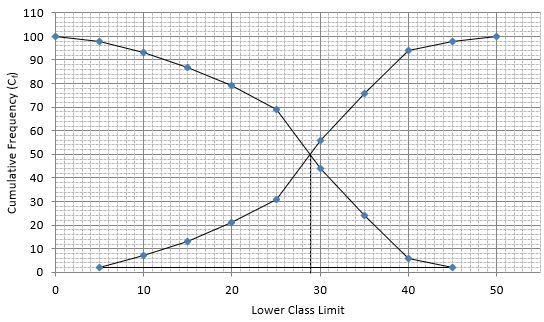
Q.9. The marks obtained by 100 students of a class in an examination are given below:

Draw cumulative frequency curves by using (i) 'less than' series and (ii) 'more than' series.
Hence, find the median.
(i) The frequency distribution table for ‘less than’ type is:
(ii) The frequency distribution table for ‘more than’ type is:
Plotting points for ‘less - than ogive’ and ‘more - than ogive’ on the graph,
In this type of graph where ‘less than ogive’ and more than ogive’ are plotted in the same graph, median is found on x - axis by the intersection of these two ogives.
Here, median = 29.5.
Q.10. From the following data, draw the two types of cumulative frequency curves and determine the median.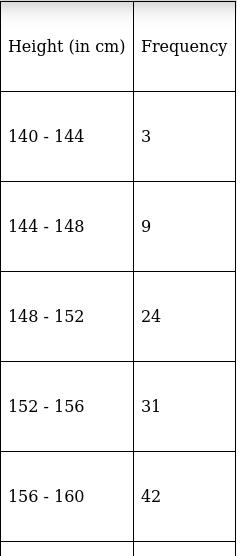

(i) The frequency distribution table for ‘less than’ type is:
(ii) The frequency distribution table for ‘more than’ type is:
Plotting points for ‘less - than ogive’ and ‘more - than ogive’ on the graph,
In this type of graph where ‘less than ogive’ and more than ogive’ are plotted in the same graph, median is found on x - axis by the intersection of these two ogives.
Here, median = 166
Exercise: 9f
Q.1. Write the median class of the following distribution:
To find median class,
Assume Σfi = N = Sum of frequencies,
fi = frequency
and Cf = cumulative frequency
Lets form a table.
So, N = 50
⇒ N/2 = 50/2 = 25
The cumulative frequency just greater than (N/2 = ) 25 is 26, so the corresponding median class is 30 - 40.
Hence, median class = 30 - 40
Q.2. What is the lower limit of the modal class of the following frequency distribution?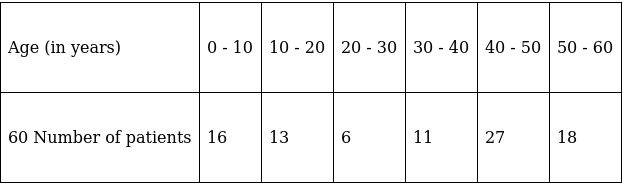
Here, the maximum class frequency is 27.
The class corresponding to this frequency is the modal class. ⇒ modal class = 40 - 50
∴ lower limit of the modal class (l) = 40
Q.3. The monthly pocket money of 50 students of a class are given in the following distribution:
Find the modal class and also give class mark of the modal class.
Here, the maximum class frequency is 30.
The class corresponding to this frequency is the modal class. ⇒ modal class = 150 - 200
∴ lower limit of the modal class (l) = 150
The class mark is found by,
∴ Class mark is 175.
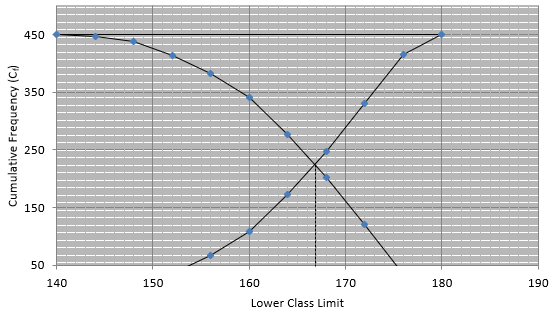
Q.4. A data has 25 observations arranged in a descending order. Which observation represents the median?
Since we have 25 observations, that is odd number of observations, median is found at
position.
So since, n = 25
⇒ Median will be found atposition. ⇒ Median = 13th observation.
Q.5. For a certain distribution, mode and median were found to be 1000 and 1250 respectively. Find mean for this distribution using an empirical relation.
Given: mode = 1000 and median = 1250
The empirical relationship between mean, median and mode is,
Mode = 3(Median) – 2(Mean)
⇒ 2(Mean) = 3(Median) – Mode
⇒ Mean = [3(Median) – Mode]/2
⇒ Mean = [3(1250) – 1000]/2
⇒ Mean = [3750 – 1000]/2 = 2750/2 = 1375
∴ mean = 1375
Q.6. In a class test, 50 students obtained marks as follows:
Find the modal class and the median class.
Here, the maximum class frequency is 25.
The class corresponding to this frequency is the modal class. ⇒ modal class = 40 - 60
To find median class,
Assume Σfi = N = Sum of frequencies,
fi = frequency
and Cf = cumulative frequency
Lets form a table.
So, N = 50
⇒ N/2 = 50/2 = 25
The cumulative frequency just greater than (N/2 = ) 25 is 35, so the corresponding median class is 40 - 60.
∴ modal class = 40 - 60 and median class = 40 - 60
Q.7. Find the class marks of classes 10 - 25 and 35 - 55.
Class mark is given by
Class mark of class 10 - 25 =
Class mark of class 35 - 55 =
∴ Class mark of class 10 - 25 is 17.5 and 35 - 55 is 45.
Q.8. While calculating the mean of a given data by the Assumed - mean method, the following values were obtained: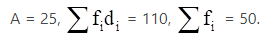
Find the mean.
We have got
A = 25, Σfi = 50 & Σfidi = 110
∵ By Assumed - mean method, mean is given by= 27.2
Thus, mean is 27.2
Q.9. The distributions X and Y with Total number of observations 36 and 64, and mean 4 and 3 respectively are combined. What is the mean of the resulting distribution X + Y?
According to the question,
⇒ X = 36 × 4 = 144 and Y = 64 × 3 = 192
We have, X = 144 and Y = 192
Mean of distribution (X + Y = 144 + 192 = ) 336 is,
Mean = 336/(36 + 64) = 336/100 = 3.36
Hence, mean = 3.36
Q.10. In a frequency distribution table with 12 classes, the class - width is 2.5 and the lowest class boundary is 8.1, then what is the upper class boundary of the highest class?
Given: number of classes = 12,
Class width = 2.5, and
Lowest class boundary = 8.1
Upper class is given by,
Upper class boundary = Lower class boundary + (width × number of classes)
Substituting values,
⇒ Upper class boundary = 8.1 + (2.5 × 12)
⇒ Upper class boundary = 8.1 + 30 = 38.1
Hence, upper class boundary is 38.1
Q.11. The observations 29, 32, 48, 50, x, x + 2, 72, 78, 84, 95 are arranged in ascending order. What is the value of x if the median of the data is 63?
Since there are 10 observations, that is, even number of observations, median is found by taking average of
observations.
So, median is found at average ofobservations.
(5)th observation = x and (6)th observation = x + 2
Taking average,
Median = (x + x + 2)/2
⇒ 63 = (2x + 2)/2 [∵ given is median = 63]
⇒ 126 = 2x + 2
⇒ 2x = 126 – 2
⇒ 2x = 124
⇒ x = 124/2 = 62
∴ x = 62
Q.12. The median of 19 observations is 30. Two more observations are made and the values of these are 8 and 32. Find the median of the 21 observations taken together.
As median is the “middle” number of the sorted list of numbers, and given is median of 19 observations observed to be 30.
⇒ 30 is the middle most value amongst 19 observations.
If two more observations (8 and 32) are added, where 8 is less than 30 and 32 is more than 30. 30 is still the middlemost value as the two values are added on either side of 30.
Hence, median of 21 observations are 30.
Q.13. If the median of  where x > 0, is 8, find the value of x.
where x > 0, is 8, find the value of x.
Arranging the values x/5, x/4, x/2, x and x/3 in ascending order, we get x/5, x/4, x/3, x/2 and x
Here, median is x/3 as it is the middle value amongst all values.
Given: median = 8
⇒ x/3 = 8
⇒ x = 24
Hence, x = 24.
Q.14. What is the cumulative frequency of the modal class of the following distribution?
Here, the maximum class frequency is 23.
The class corresponding to this frequency is the modal class. ⇒ modal class = 12 - 15
Lets form a table.
Since, modal class = 12 - 15, the corresponding cumulative frequency is 53.
Q.15. Find the mode of the given data:
Here, the maximum class frequency is 18.
The class corresponding to this frequency is the modal class. ⇒ modal class = 40 - 60
∴ lower limit of the modal class (l) = 40
Modal class size (h) = 20
Frequency of the modal class (f1) = 18
Frequency of class preceding the modal class (f0) = 6
Frequency of class succeeding the modal (f2) = 10
Mode is given by,
⇒ Mode = 40 + 12 = 52
Hence, the mode is 52.
Q.16. The following are the ages of 300 patients getting medical treatment in a hospital on a particular day: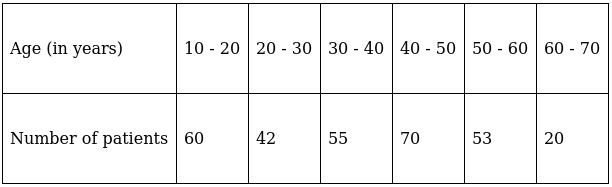
Form a 'less than type' cumulative frequency distribution.
In a ‘less than type’ cumulative frequency distribution, upper limit of the classes are considered.
It is given by,
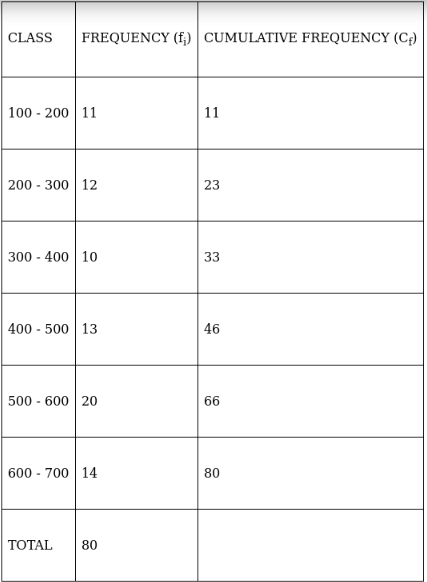
Q.17. In the following data, find the values of p and q. Also, find the median class and modal class.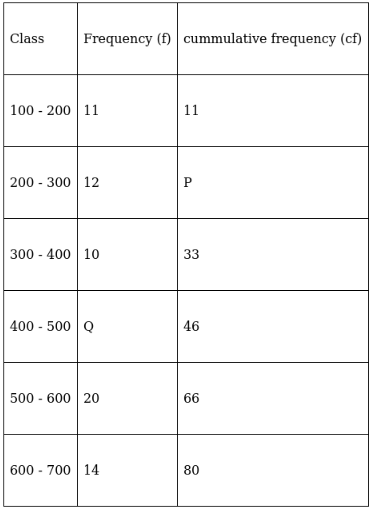
To find p and q, solve by finding cumulative frequency,
⇒ p = 11 + 12 = 23
And 46 = 33 + q ⇒ q = 46 – 33 = 13
∴ p = 23 and q = 13
Lets form the table again,
For modal class,
Here, the maximum class frequency is 20.
The class corresponding to this frequency is the modal class. ⇒ modal class = 500 - 600
To find median class,
Assume Σfi = N = Sum of frequencies,
fi = frequency
and Cf = cumulative frequency
So, N = 80
⇒ N/2 = 80/2 = 40
The cumulative frequency just greater than (N/2 = ) 40 is 46, so the corresponding median class is 400 - 500.
∴ modal class = 500 - 600 and median class = 400 - 500
Q.18. The following frequency distribution gives the monthly consumption of electricity of 64 consumers of a locality.
Form a 'more than type' cumulative frequency distribution.
In a ‘less than type’ cumulative frequency distribution, lower limits of the classes are considered.
It is given by,
Q.19. The following table gives the life - time (in days) of 100 electric bulbs of a certain brand.
From this table, construct the frequency distribution table.
The frequency distribution table is:
Q.20. The following table gives the frequency distribution of the percentage of marks obtained by 2300 students in a competitive examination.
(a) Convert the given frequency distribution into the continuous form.
(b) Find the median class and write its class mark.
(c) Find the modal class and write its cumulative frequency.
(a) To convert the given frequency distribution into continuous form, adjust the end - limits of each class.
(b) To find median class,
Assume Σfi = N = Sum of frequencies,
fi = frequency
and Cf = cumulative frequency
So, N = 2300
⇒ N/2 = 2300/2 = 1150
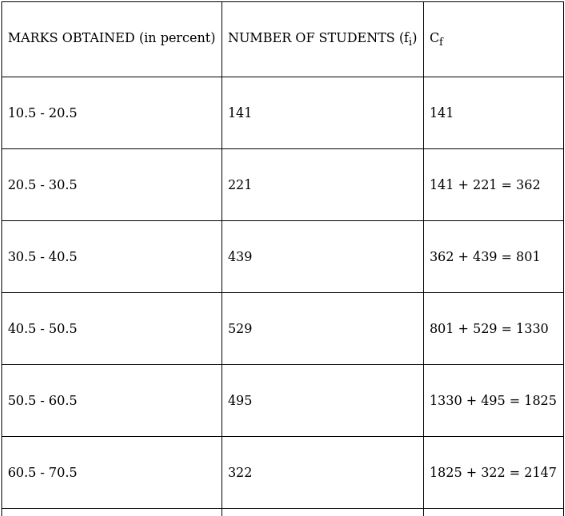
The cumulative frequency just greater than (N/2 = ) 1150 is 1825, so the corresponding median class is 50.5 - 60.5.
∴ Median class = 50.5 - 60.5
The class mark of 50.5 - 60.5 is
(c) For modal class,
Here, the maximum class frequency is 529.
The class corresponding to this frequency is the modal class. ⇒ modal class = 40.5 - 50.5
The cumulative frequency corresponding to the modal class is 1330
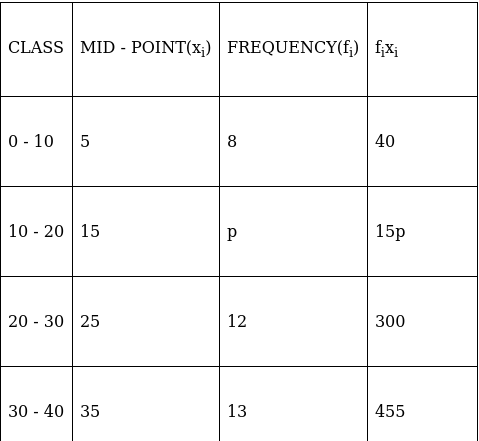
Q.21. If the mean of the following distribution is 27, find the value of p.
We have got
Σfi = 43 + p and Σfixi = 1245 + 15p
∵ mean is given by(∵ given: mean of pocket allowance is 27)
⇒ 1161 + 27p = 1245 + 15p
⇒ 27p – 15p = 1245 – 1161
⇒ 12p = 84
⇒ p = 84/12
⇒ p = 7
Thus, p = 7
Q.22. Calculate the missing frequency from the following distribution, it being given that the median of the distribution is 24.
Given: Median = 24
Let the unknown frequency be x.
Assume
Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table, where x is the unknown frequency.
Median = 24 (as already mentioned in the question)
24 lies between 20 - 30 ⇒ Median class = 20 - 30
∴ l = 20, h = 10, f = x, N/2 = (55 + x)/2 and Cf = 30
Median is given by,
⇒ 24 – 20 = (5x – 25)/x
⇒ 4x = 5x – 25
⇒ 5x – 4x = 25
⇒ x = 25
Formative Assessment (unit Test)
Q.1. Which one of the following measures is determined only after the construction of cumulative frequency distribution?
(a) Mean
(b) Median
(c) Mode
(d) None of these
Mean and mode does not require construction of cumulative frequency, but median necessarily requires construction of cumulative frequency, unless it is raw data (in which median is the (n/2)th value, when there are n number of observations; and the average of (n/2)th and (n/2 + 1)th values, when there are n observations).
Q.2. If the mean of a data is 27 and its median is 33 then the mode is
(a) 30
(b) 43
(c) 45
(d) 47
Given: mean = 27 and median = 33
We have to find the value of mode.
Empirical relationship is given by,
Mode = 3(Median) – 2(Mean)
⇒ Mode = 3(33) – 2(27)
⇒ Mode = 99 – 54 = 45
Q.3. Consider the following distribution:
The Sum of the lower limits of the median class and the modal class is
(a) 15
(b) 25
(c) 30
(d) 35
We need to find – (1) Median class
(2) Modal class
First we’ll find (1) Median class.
To find median class,
Assume Σfi = N = Sum of frequencies,
fi = frequency of class intervals
and Cf = cumulative frequency
Lets form a table.
So, N = 66
⇒ N/2 = 66/2 = 33
The cumulative frequency just greater than (N/2 = ) 33 is 37, so the corresponding median class is 10 - 15.
∴ median class is 10 - 15.
To find (2) Modal class,
Here, the maximum class frequency is 20.
The class corresponding to this frequency is the modal class. ⇒ modal class = 15 - 20
Lower limit of median = 10 and lower limit of mode = 15
Sum = 10 + 15 = 25
Q.4. Consider the following frequency distribution: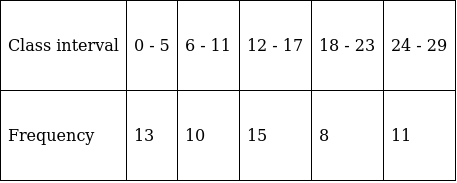
The upper limit of the median class is
(a) 16.5
(b) 18.5
(c) 18
(d) 17.5
To find median class,
Assume Σfi = N = Sum of frequencies,
fi = frequency of class intervals
and Cf = cumulative frequency
Lets convert this data into exclusive type of data.
So, N = 57
⇒ N/2 = 57/2 = 28.5
The cumulative frequency just greater than (N/2 = ) 28.5 is 38, so the corresponding median class is 11.5 - 17.5.
∴ Upper limit of this median class = 17.5
Q.5. If the mean and mode of a frequency distribution be 53.4 and 55.2 respectively, find the median.
Given: mean = 53.4 and mode = 55.2
We have to find the median.
By empirical formula,
Mode = 3(Median) – 2(Mean)
⇒ 3(Median) = Mode + 2(Mean)
⇒ Median = [Mode + 2(Mean)]/3
⇒ Median = [55.2 + 2(53.4)]/3
⇒ Median = [55.2 + 106.8]/3
⇒ Median = 162/3 = 54
∴ Median = 54
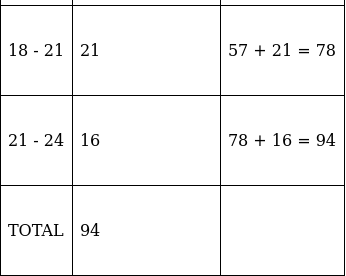
Q.6. In the table given below, the times taken by 120 athletes to run a 100 - m - hurdle race are given.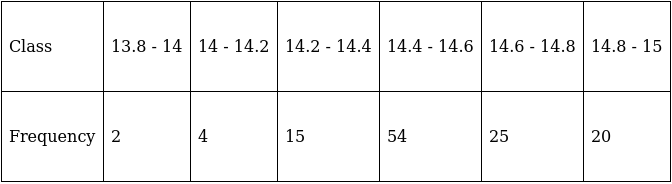
Find the number of athletes who completed the race in less than 14.6 seconds.
We need to form a ‘less than type’ table to solve this.
Here, cumulative frequency shows number of athletes taking different time intervals to run a 100 - m - hurdle race.
So by the table, there are 75 athletes who completed the race in less than 14.6 seconds.
Q.7. Consider the following frequency distribution:
Find the upper limit of the median class.
To find median class,
Assume Σfi = N = Sum of frequencies,
fi = frequency of class intervals
and Cf = cumulative frequency
Lets convert this data into exclusive type of data.
So, N = 57
⇒ N/2 = 57/2 = 28.5
The cumulative frequency just greater than (N/2 = ) 28.5 is 38, so the corresponding median class is 11.5 - 17.5.
∴ Upper limit of this median class = 17.5
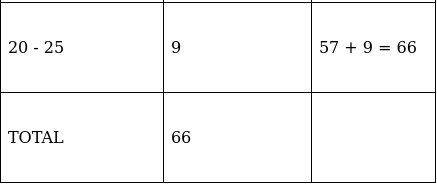
Q.8. The annual profits earned by 30 shops of a shopping complex in a locality are recorded in the table shown below:

If we draw the frequency distribution table for the above data, find the frequency corresponding to the class 20 - 25.
To find frequency corresponding to 20 - 25 class, we need to convert ‘more than or equal to’ type data into class intervals.
Observe in the table above, frequency corresponding to the class 20 - 25 is 4.
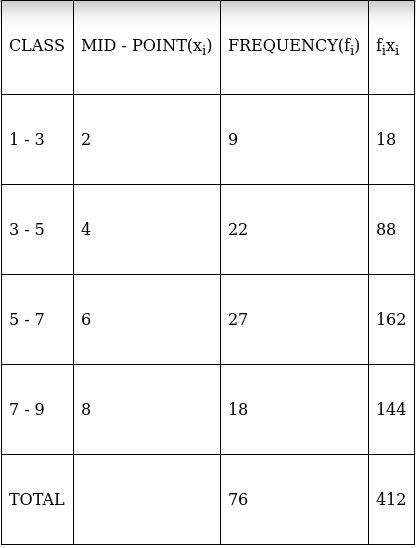
Q.9. Find the mean of the following frequency distribution: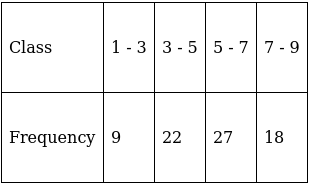
For equal class intervals, we will solve by finding mid points of these classes using direct method.
We have got
Σfi = 76 & Σfixi = 412
∵ mean is given by= 5.421
Thus, mean is 5.421
Q.10. The maximum bowling speeds (in km/hr) of 30 players at a cricket coaching centre are given below: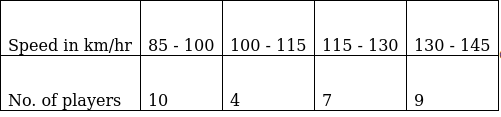
Calculate the median bowling speed.
To find median, Assume
Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
So, N = 30
⇒ N/2 = 30/2 = 15
The cumulative frequency just greater than (N/2 = ) 15 is 21, so the corresponding median class is 115 - 130 and accordingly we get Cf = 14(cumulative frequency before the median class).
Now, since median class is 115 - 130.
∴ l = 115, h = 15, f = 7, N/2 = 15 and Cf = 14
Median is given by,
= 115 + 2.14
= 117.14
Thus, median is 117.14 km/hr.
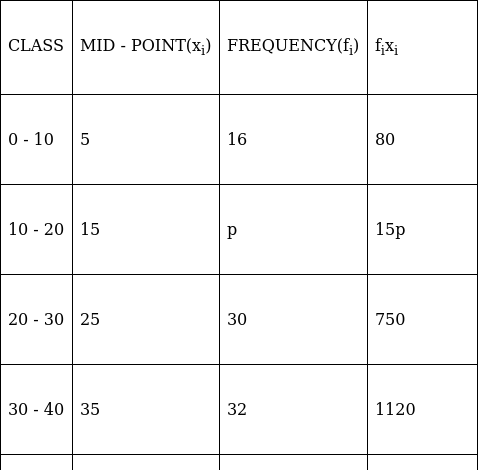
Q.11. The arithmetic mean of the following frequency distribution is 50.
Find the value of p.
For equal class intervals, we will solve by finding mid points of these classes using direct method.
We have got
Σfi = 92 + p and Σfixi = 2580 + 15p
∵ mean is given by(∵ given: arithmetic mean is 50)
⇒ 4600 + 50p = 2580 + 15p
⇒ 50p – 15p = 2580 – 4600
⇒ 35p = 2020
⇒ p = 11
Thus, p is 11.
Q.12. Find the median of the following frequency distribution: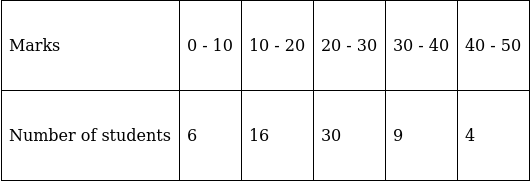
To find median, Assume
Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
So, N = 65
⇒ N/2 = 65/2 = 32.5
The cumulative frequency just greater than (N/2 = ) 32.5 is 52, so the corresponding median class is 20 - 30 and accordingly we get Cf = 22(cumulative frequency before the median class).
Now, since median class is 20 - 30.
∴ l = 20, h = 10, f = 30, N/2 = 32.5 and Cf = 22
Median is given by,
= 20 + 3.5
= 23.5
Thus, median is 23.5.
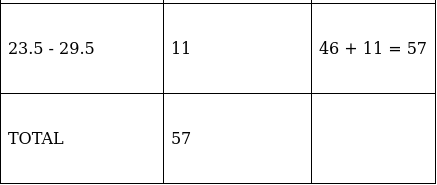
Q.13. Following is the distribution of marks of 70 students in a periodical test:
Draw a cumulative frequency curve for the above data.
The frequency distribution table for ‘less than’ type is:
Lets plot a graph of ‘less than ogive’, taking upper limits of the class intervals on x - axis and cumulative frequencies on y - axis.
Q.14. Find the median of the following data.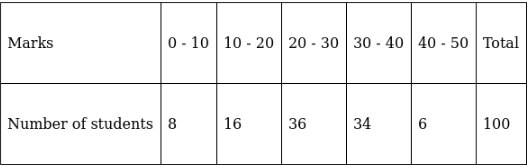
To find median, Assume
Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table and convert it into exclusive - type by adjusting from both ends of a class.
So, N = 100
⇒ N/2 = 100/2 = 50
The cumulative frequency just greater than (N/2 = ) 50 is 60, so the corresponding median class is 20 - 30 and accordingly we get Cf = 24(cumulative frequency before the median class).
Now, since median class is 20 - 30.
∴ l = 20, h = 10, f = 36, N/2 = 50 and Cf = 24
Median is given by,
= 20 + 7.22
= 27.22
Thus, median is 27.22.
Q.15. For the following distribution draw a 'less than type' ogive and from the curve find the median.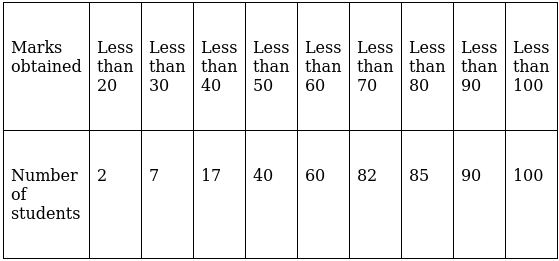
Lets plot a graph of ‘less than ogive’, taking upper limits of the class intervals on x - axis and cumulative frequencies on y - axis.
As we have N = 100 by the frequency table.
N/2 = 100/2 = 50
Mark 50 on y - axis and the corresponding point on x - axis would be the median.
The corresponding point on x - axis is 55.
Hence, median is 55.
Q.16. The median value for the following frequency distribution is 35 and the Sum of all the frequencies is 170. Using the formula for median, find the missing frequencies.
Given: Median = 35 & N = 170
Assume
Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table, where x and y are the unknown frequencies.
Median = 35 (as already mentioned in the question)
35 lies between 30 - 40 ⇒ Median class = 30 - 40
∴ l = 30, h = 10, f = 40, N/2 = (110 + x + y)/2 = 170/2 = 85 and Cf = 30 + x
Median is given by,
⇒ 35 – 30 = (55 – x)/4
⇒ 5 × 4 = 55 – x
⇒ 20 = 55 – x
⇒ x = 55 – 20 = 35 …(i)
And given that N = 170
⇒ 110 + x + y = 170
⇒ x + y = 170 – 110
⇒ x + y = 60 …(ii)
Substituting x = 35 in eq.(ii),
35 + y = 60
⇒ y = 60 – 35 = 25
Thus, the unknown frequencies are x = 35 and y = 25.
Q.17. Find the missing frequencies f1 and f2 in the table given below, it being given that the mean of the given frequency distribution is 50.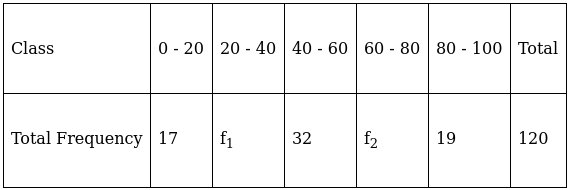
For equal class intervals, we will solve by finding mid points of these classes using direct method.
We have got
Mean = 50 and N = 120 (as given in the question)
Σfi = 68 + f1 + f2 and Σfixi = 3480 + 30f1 + 70f2
∵ mean is given by(∵ given: mean is 50)
⇒ 3400 + 50f1 + 50f2 = 3480 + 30f1 + 70f2
⇒ 50f1 – 30f1 + 50f2 – 70f2 = 3480 – 3400
⇒ 20f1 – 20f2 = 80
⇒ f1 – f2 = 4 …(i)
As given in the question, frequency(Σfi) = 120
And as calculated by us, frequency (Σfi) = 68 + f1 + f2
Equalizing them, we get
68 + f1 + f2 = 120
⇒ f1 + f2 = 120 – 68 = 52
⇒ f1 + f2 = 52 …(ii)
We will now solve equations (i) and (ii), adding them we get
(f1 + f2) + (f1 – f2) = 52 + 4
⇒ 2f1 = 56
⇒ f1 = 56/2
⇒ f1 = 28
Substitute f1 = 28 in equation (ii),
28 + f2 = 52
⇒ f2 = 52 – 28
⇒ f2 = 24
Thus, f1 = 28 and f2 = 24.
Q.18. Find the mean of the following frequency distribution using step - deviation method: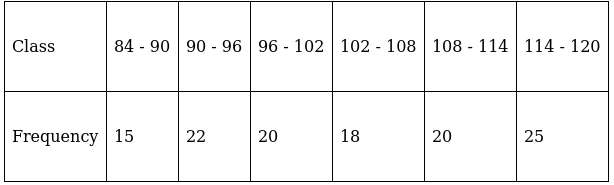
We will find the mean using step - deviation method, where A = Assumed mean and h = length of class interval.
Here, let A = 99 and h = 6
Since, the class intervals are inclusive type, we’ll first convert it into exclusive type by extending the class interval from both the ends.
We have got
A = 99, h = 6, Σfi = 120 & Σfiui = 81
∵ mean is given by
Thus, mean is 103.05.
Q.19. Find the mean, median and mode of the following data:
For equal class intervals, we will solve by finding mid points of these classes using direct method.
We have got
Σfi = 50 and Σfixi = 1500
∵ mean is given by= 30
Thus, mean is 30.
To find median, Assume
Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
We have got
So, N = 50
⇒ N/2 = 50/2 = 25
The cumulative frequency just greater than (N/2 = ) 25 is 39, so the corresponding median class is 30 - 40 and accordingly we get Cf = 24(cumulative frequency before the median class).
Now, since median class is 30 - 40.
∴ l = 30, h = 10, f = 15, N/2 = 25 and Cf = 24
Median is given by,
= 30 + 0.67
= 30.67
Thus, median is 30.67.
Since, we have got mean = 30 and median = 30.67
Applying the empirical formula,
Mode = 3(Median) – 2(Mean)
⇒ Mode = 3(30.67) – 2(30)
⇒ Mode = 92.01 – 60 = 32.01
∴ Mean = 30, Median = 30.67 and Mode = 32.01
Q.20. Draw 'less than ogive' and 'more than ogive' on a single graph paper and hence find the median of the following data: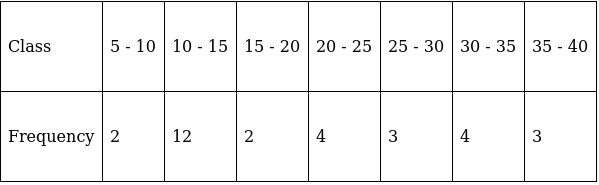
The frequency distribution table for ‘less than’ type is:
The frequency distribution table for ‘more than’ type is:
Plotting points for ‘less - than ogive’ and ‘more - than ogive’ on the graph,
In this type of graph where ‘less than ogive’ and more than ogive’ are plotted in the same graph, median is found on x - axis by the intersection of these two ogives.
Here, median = 15.5
Q.21. The production yield per hectare of wheat of some farms of a village are given in the following table:
Draw a less than type ogive and a more than type ogive for this data.
The frequency distribution table for ‘less than’ type is:
Lets plot the graph of ‘less than ogive’, taking upper limits of the class intervals on x - axis and cumulative frequencies on y - axis.
Lets plot a graph of ‘more than’ ogive, taking lower limits of the class intervals on x - axis and cumulative frequencies on y - axis.
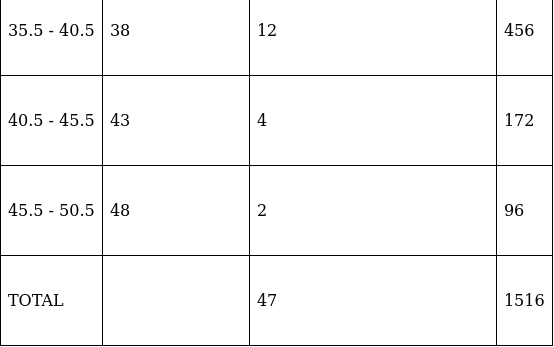
Q.22. The following table gives the marks obtained by 50 students in a class test: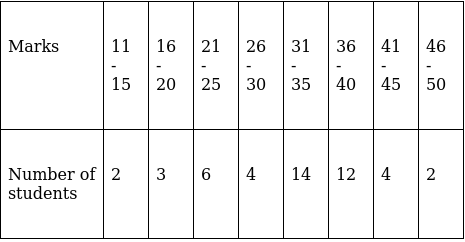
Calculate the mean, median and mode for the above data.
For equal class intervals, we will solve by finding mid points of these classes using direct method.
We have got
Σfi = 47 and Σfixi = 1516
∵ mean is given by32.26
Thus, mean is 32.26.
To find median, Assume
Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
We have got
So, N = 47
⇒ N/2 = 47/2 = 23.5
The cumulative frequency just greater than (N/2 = ) 23.5 is 29, so the corresponding median class is 30.5 - 35.5 and accordingly we get Cf = 15(cumulative frequency before the median class).
Now, since median class is 30.5 - 35.5.
∴ l = 30.5, h = 5, f = 14, N/2 = 23.5 and Cf = 15
Median is given by,
= 30 + 3.03
= 33.03
Thus, median is 33.03.
Since, we have got mean = 32.26 and median = 33.03
Applying the empirical formula,
Mode = 3(Median) – 2(Mean)
⇒ Mode = 3(33.03) – 2(32.26)
⇒ Mode = 99.09 – 64.52 = 34.57
∴ Mean = 32.26, Median = 33.03 and Mode = 34.57
|
53 docs|15 tests
|
|
53 docs|15 tests
|

|
Explore Courses for Class 10 exam
|

|

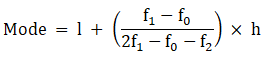

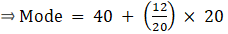
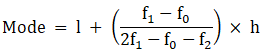

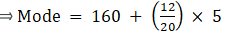



 = 161.17
= 161.17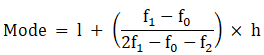


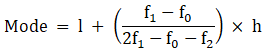
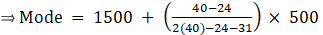
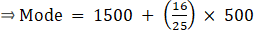
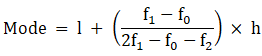

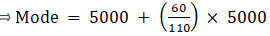
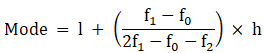




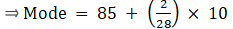


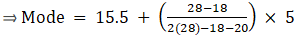
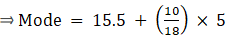


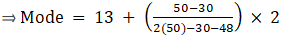


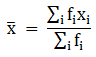
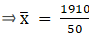
 = 38.2
= 38.2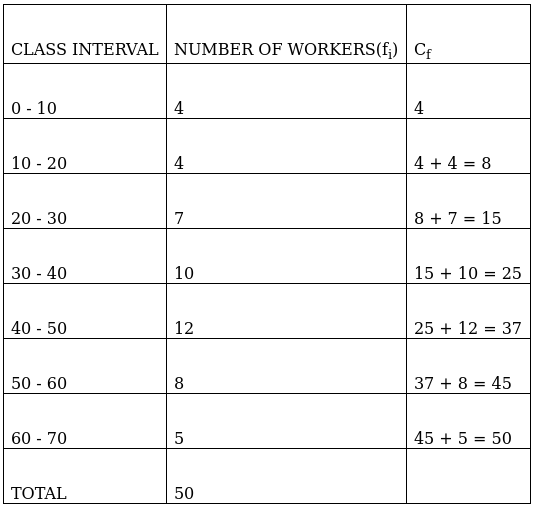

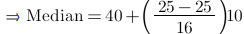



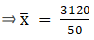
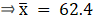



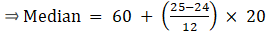

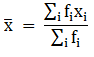
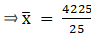
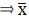 = 169
= 169


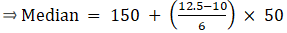

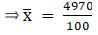
 = 49.7
= 49.7





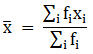

 = 149.8
= 149.8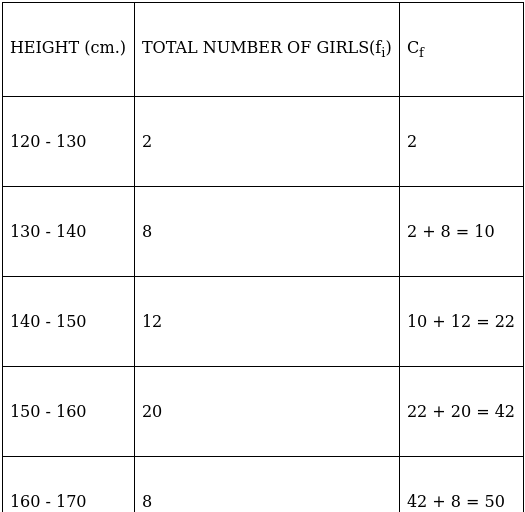


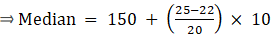



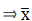 = 145.2
= 145.2

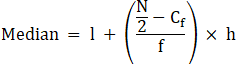




 = 205
= 205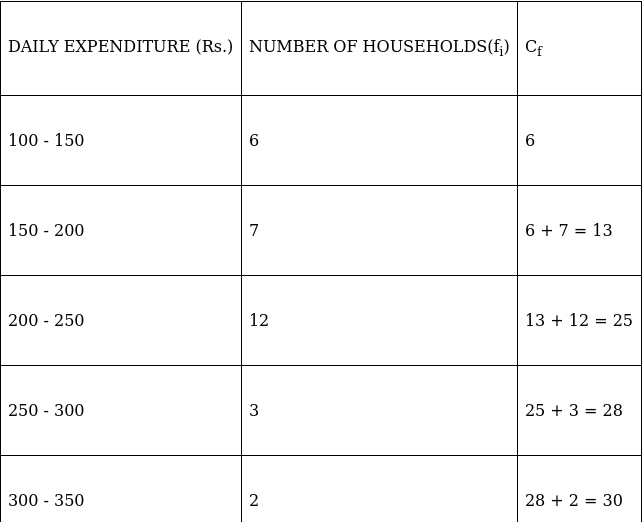

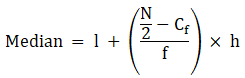















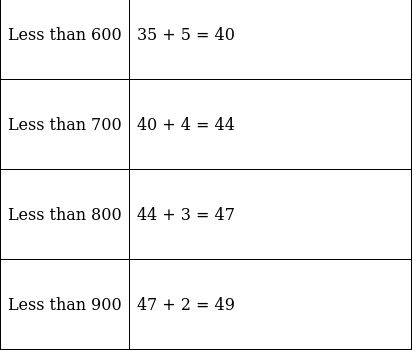
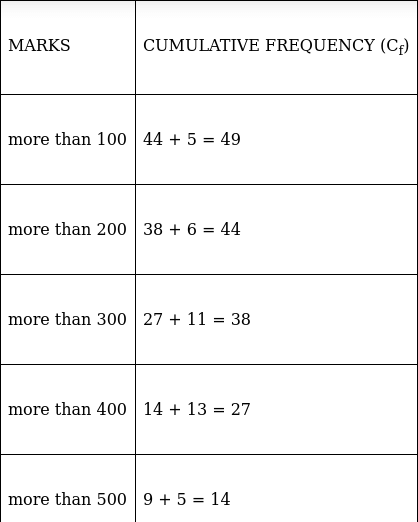
















 position.
position.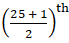 position. ⇒ Median = 13th observation.
position. ⇒ Median = 13th observation.

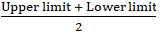
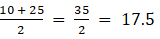
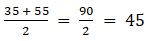


 = 27.2
= 27.2
 observations.
observations.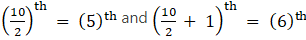 observations.
observations.











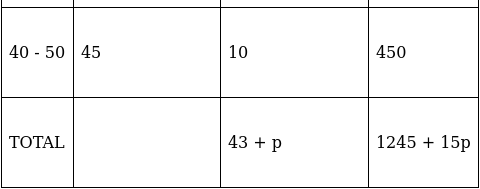

 (∵ given: mean of pocket allowance is 27)
(∵ given: mean of pocket allowance is 27)



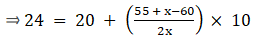




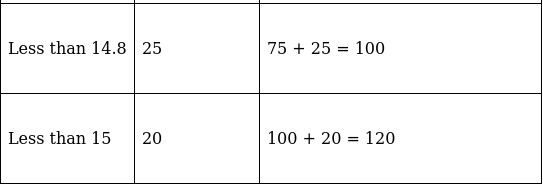



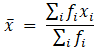
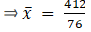
 = 5.421
= 5.421




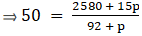 (∵ given: arithmetic mean is 50)
(∵ given: arithmetic mean is 50)

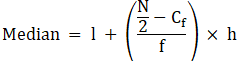
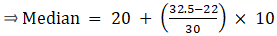



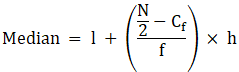





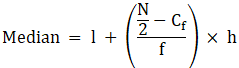



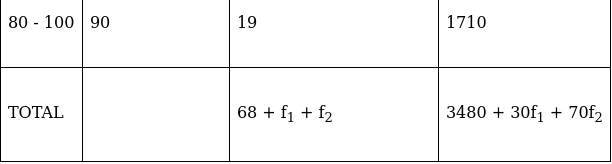

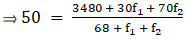 (∵ given: mean is 50)
(∵ given: mean is 50)

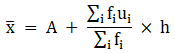
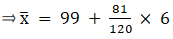
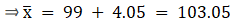



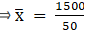
 = 30
= 30




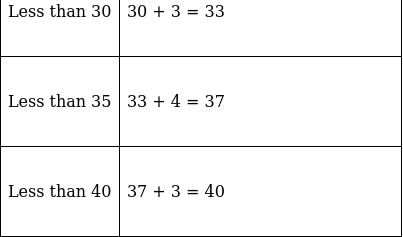









 32.26
32.26