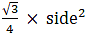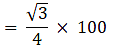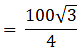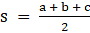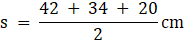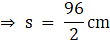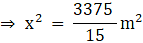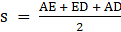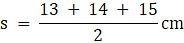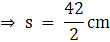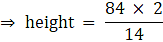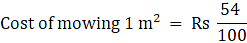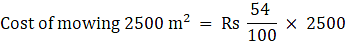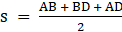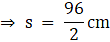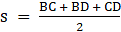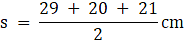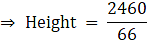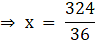RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 3 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download

Q.1. In the given figure ABCD is quadrilateral in which ∠ABC = 90°, ∠BDC = 90°, AC = 17 cm, BC = 15 cm, BD = 12 cm and CD = 9 cm. The area of quad ABCD is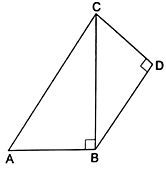

(a) 102 cm²
(b) 114 cm²
(c) 95 cm²
(d) 57 cm²

Given:
AC = 17 cm
BC = 15 cm
BD = 12 cm
CD = 9 cm.
∠ABC = 90°
∠BDC = 90°
In ∆ABC,
Using Pythagoras theorem,
AB² + BC² = AC²
⇒ AB² = AC²- BC²
⇒ AB = √( AC²- BC²)
⇒ AB = √( 17²- 15²)
⇒ AB = √(289-225)
⇒ AB = √64
⇒ AB = 8 cm
Therefore,
Area of ∆ABC = 1/2 × AB × BC
= 1/2 × 8 × 15
= 60 cm²
And,
In ∆BDC,
Area of ∆BDC = 1/2 × BD × DC
= 1/2 × × 12 × 9
= 54 cm²
Therefore,
Area of quadrilateral ABCD = Area of ∆ABC + Area of ∆BDC
= 60 cm² + 54 cm²
= 114 cm²

Q.2. In the given figure ABCD is a trapezium in which AB = 40 m, BC = 15 m, CD = 28 m, AD = 9 m and CE ⊥ AB. Area of trap. ABCD is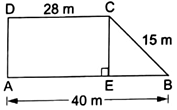

(a) 306 m²
(b) 316 m²
(c) 296 m²
(d) 284 m²

ABCD is a trapezium in which AB = 40 m, BC = 15 m, CD = 28 m, AD = 9 m and CE ⊥ AB.
Area of trap. ABCD

AB = 40 m, BC = 15 m, AD = 9 m and CD = 28 m.
In trapezium ABCD,
Area of trapezium = 1/2 × sum of parallel sides × distance between them
= 1/2 × (28 + 40) × 9
= 1/2 × 68 × 9
= 306 m²

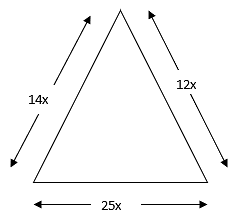
Q.3. The sides of a triangle are in the ratio 12 : 14 :25 and its perimeter is 25.5 cm. The largest side of the triangle is
(a) 7 cm
(b) 14 cm
(c) 12.5 cm
(d) 18 cm

Given: Ratio of Sides = 12: 14: 25
Perimeter = 25.5 cm
Let the sides be,
a = 12x cm
b = 14x cm
c = 25x cm

We know that,
Perimeter of a triangle = a + b + c
⇒ 25.5 cm = 12x cm + 14x cm + 25x cm
⇒ 25.5 cm = 51x cm

⇒ x = 0. 5
Therefore,
a = 12x cm = 12 × 0.5 cm = 6 cm
b = 14x cm = 14 × 0.5 cm = 7 cm
c = 25x cm = 25 × 0.5 cm = 12.5 cm
Clearly largest side is c = 12.5 cm

Q.4. The parallel sides of a trapezium are 9.7 cm and 6.3 cm, and the distance between them is 6.5 cm. The area of the trapezium is
(a)104 cm²
(b) 78 cm²
(c) 52 cm²
(d) 65 cm²

Given:
Side 1 = 9.7 cm
Side 2 = 6.3 cm
Distance between sides = 6.5 cm

Area of trapezium = 1/2 × sum of parallel sides × distance between them
= 1/2 × (9.7 + 6.3) × 6.5
= 1/2 × 16 × 6.5
= 52 cm²

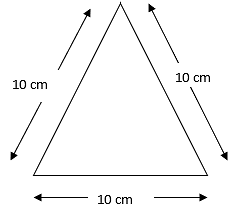
Q.5. Find the area of an equilateral triangle having each side of length 10 cm. [Take √3 = 1.732.]

Given:
Side of an equilateral triangle = 10 cm

Area of equilateral triangle =



= 25√3
= 25 × 1.732
= 43.3 cm²

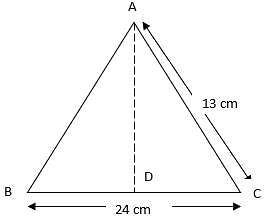
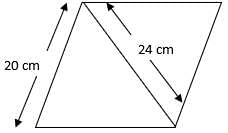
Q.6. Find the area of an isosceles triangle each of whose equal side is 13 cm and whose base is 24 cm.

Given:
Side AB = Side AC = 13 cm
Base = 24 cm

In ∆ADC (right-angled),
DC = 12 cm
By Pythagoras theorem,
AD² + DC² = AC²
⇒ AD² = AC² - DC²
⇒ AD² = 13² - 12²
⇒ AD² = 169 – 144 = 25
⇒ AD = 5 cm
Now,
Area of triangle = 1/2 × base × height
= 1/2 × BC × AD
= 1/2 × 24 × 5
= 60 cm²

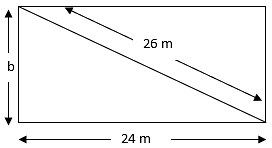
Q.7. The longer side of rectangular hall is 24 m and the length of its diagonal is 26 m. Find the area of the hall.

Given:
Length (l) = 24 m
Diagonal = 26 m
Let breadth be b

We know that,
Base² + Perpendicular² = Hypotenuse²
⇒ 24² + b² = 26²
⇒ b² = 26² - 24²
⇒ b² = 676 - 576 = 100
⇒ b= 10 m
Area of rectangle = Length × Breadth
= 24 m × 10 m
= 240 m²

Q.8. The length of the diagonal of a square is 24 cm. Find its area.

Given:
Length of diagonal = 24 cm
Let the side of square = x cm

We know that,
Hypotenuse² = Base² + Perpendicular²
⇒ 24² = x² + x²
⇒ 576 = 2x²

⇒ x² = 288
⇒ x = 12√2 cm
Now,
Area of a square = side²
= (12√2 cm)²
= 288 cm²

Q.9. Find the area of a rhombus whose diagonal are 48 cm and 20 cm long.

Given:
Length of diagonal 1 (d₁) = 48 cm
Length of diagonal 2 (d₂) = 20 cm

Area of rhombus = 1/2 × d₁ × d₂
= 1/2 × 48 cm × 20 cm
= 480 cm²

Q.10. Find the area of a triangle whose sides are 42 cm, 34 cm and 20 cm.

Given: Side 1 = a (let) = 42 cm
Side 2 = b (let) = 34 cm
Side 3 = c (let) = 20 cm

We know that,
Area of a scalene triangle = √(s(s-a)(s-b)(s-c))
Where, 


⇒ s = 48 cm
Now,
Area of a scalene triangle = √(48cm × (48-42)cm × (48-34)cm × (48-20)cm)
= √(48cm × 6cm × 14cm × 28cm)
= √112896 cm²
= 336 cm²

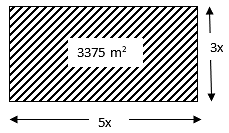
Q.11. A lawn is in the form of a rectangle whose sides are in the ratio 5 : 3 and its area is 3375 m². Find the cost of fencing the lawn at RS. 20 per metre.

Given: Cost of fencing lawn = Rs 20 per metre.
Area of lawn = 3375 m²
Length : Breadth = 5:3
Let,
Length = 5x
Breadth = 3x

We know that,
Area of lawn = Length × Breadth
⇒ 3375 m² = 5x × 3x
⇒ 3375 m² = 15x²

⇒ x² = 225 m²
⇒ x = 15 m
Therefore,
Length = 5x = 5 × 15 = 75 m
Breadth = 3x = 3 × 15 = 45 m
Now,
Perimeter of lawn = 2(length + breadth)
= 2(75 m + 45 m)
= 2 × 120 m
= 240 m
Hence,
Cost of Fencing = 240 m × Rs 20 per meter
= Rs 4800

Q.12. Find the area of a rhombus each side of which measurers 20 cm and one of whose diagonals is 24 cm.

Given:
Length of diagonal 1 (d₁) = 24 cm
Side = 20 cm

Let, Length of diagonal 2 be d₂
We know that,
Side of rhombus = 1/2 × √(d₁² + d₂² )
⇒ 20 = 1/2 × √(24² + d₂² )
⇒ 20 × 2 = √(576 + d₂² )
⇒ 40 = √(576 + d₂²)
Squaring both sides,
⇒ 1600 = 576 + d₂²
⇒ d₂² = 1600-576
⇒ d₂² = 1024
⇒ d² = 32 cm
Now,
Area of rhombus= 1/2 × d₁ × d₂
= 1/2 × 24 × 32
= 384 cm²

Q.13. Find the area of a trapezium whose parallel sides are 11 cm and 25 cm long and non-parallel sides are 15 cm and 13 cm.

Given:
AB (say) = 11 cm
DC (say) = 25 cm
AD (say) = 15 cm
BC (say) = 13 cm
Draw AE ∥ BC

Now the trapezium is divided into a triangle ADE and a parallelogram AECB.
Since, AECB is a parallelogram
Therefore, AE = BC = 13 cm
And, AB = EC
DE = DC – EC( = AB) = 25 – 11 = 14 cm
Now,
We know that,
Area of a scalene triangle (∆AED) = √(s(s-AE)(s-ED)(s-AD))
Where, 


⇒ s = 21 cm
Now,
Area of a scalene triangle = √(21cm × (21-13)cm × (21-14)cm × (21-15)cm)
= √(21cm × 8cm × 7cm × 6cm)
= √7056 cm²
= 84 cm²
Also,
Area of a triangle = 1/2 × base × height
⇒ 84 = 1/2 × 14 × height

⇒ height = 12 cm
Now,
Area of a parallelogram = base × height
= 11 cm × 12 cm
= 132 cm2
Now,
Area of Trapezium ABCD = Area of ∆ADE + Area of a parallelogram ABCE
= 84 cm² + 132 cm²
= 216 cm²

Q.14. The adjacent sides of a llgm ABCD measure 34 cm and 20 cm and the diagonal AC is 42 cm long. Find the area of the ll gm.

Given:
AB = 34 cm
BC = 20 cm
AC = 42 cm
The diagonal of a parallelogram divides it into two equal triangles.
Therefore,
Area of ABCD = 2 × Area of ∆ABC
Now,
We know that,
Area of a scalene triangle = √(s(s-AC)(s-AB)(s-BC))
Where, 


⇒ s = 48cm
Now,
Area of a scalene triangle = √(48cm × (48-42)cm × (48-34)cm × (48-20)cm)
= √(48cm × 6cm × 14cm × 28cm)
= √112896 cm²
= 336 cm²
Therefore,
Area of ABCD = 2 × 336 cm²
= 672 cm²

Q.15. The cost of fencing a square lawn at RS. 14 per metre is RS. 2800. Find the cost of mowing the lawn at RS. 54 per 100m².

Given:
Rate = RS. 14 per metre
Total Cost = RS. 2800
Rate of mowing = RS. 54 per 100 m²
Let the side of square field be s

Now,

= 2800/14
= 200 m
Perimeter = 4 × side
⇒ 200 m = 4 × s

⇒ s = 50 m
Now,
Area = side²
= (50 m) ²
= 2500 m²
Therefore,
Cost of mowing 100 m² = Rs 54


= Rs 1350

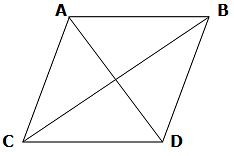
Q.16. Find the area of quad. ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm and diag. BD = 20 cm.

Given:
DB = 20 cm
AB = 42 cm
AD = 34 cm
CD = 29 cm
CB = 21 cm
In ∆ABD(scalene),
Area of a scalene triangle = √(s(s-AB)(s-BD)(s-AD))
Where, 


⇒ s = 48 cm
Now,
Area of a scalene triangle = √(48cm × (48-42)cm × (48-20)cm × (48-34)cm)
= √(48 cm × 6 cm × 28 cm × 14 cm)
= √112896 cm²
= 336 cm²
Similarly,
In ∆BCD (scalene),
Area of a scalene triangle = √(s(s-BC)(s-CD)(s-BD))
Where, 


⇒ s = 35 cm
Now,
Area of a scalene triangle = √(35 cm × (35-29)cm × (35-20)cm × (35-21)cm)
= √(35 cm × 6 cm × 15 cm × 14 cm)
= √44100 cm²
= 210 cm²
Now,
Area of quadrilateral ABCD = Area of ∆ABD + Area of ∆BCD
= 336 cm² + 210 cm²
= 546 cm²

Q.17. A parallelogram and a rhombus are equal in area. The diagonals of the rhombus measure 120 m and 44 m. If one if the sides of the ll gm is 66 m long, find its corresponding altitude.

Given:
Diagonal 1 (d₁) of rhombus = 120 m
Diagonal 2 (d₂) of rhombus = 44 m
Side of parallelogram = 66 m
Area of rhombus = 1/2 × d₁ × d₂
= 1/2 × 120 m × 44 m
= 2640 m²
Now,
Area of parallelogram = Base × Height
⇒ 2640 m² = 66 m × Height

⇒ Height = 40 m

Q.18. The diagonals of a rhombus are 48 cm and 20 cm long. Find the perimeter of the rhombus.

Given:
Length of diagonal 1 (d1) = 48cm
Length of diagonal 2 (d2) = 20 cm

Side of rhombus = 1/2 × √(d₁² + d₂² )
= 1/2 × √(48² + 20² )
= 1/2 × √(2304 + 400)
= 1/2 × √2704
= 1/2 × 52
= 26 cm
Therefore,
Perimeter of rhombus = 4 × Side of rhombus
= 4 × 26 cm
= 104 cm

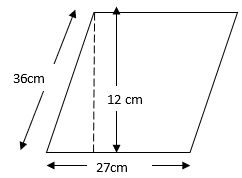
Q.19. The adjacent sides of a parallelogram are 36 cm and 27 cm in length. If the distance between the shorter sides is 12 cm, find the distance between the longer sides.

Given:
Longer side = 36 cm
Shorter side = 27 cm
Distance between Shorter sides = 12 cm

Let, Distance between Longer sides = x cm
Now,
Area of parallelogram = Shorter Side × Distance between Longer sides
= 27 cm × 12 cm
= 324 cm²
Also,
Area of parallelogram = Longer side × Distance between Longer sides
⇒ 324 cm² = 36 cm × x cm

⇒ x = 9 cm
Hence,
Distance between Shorter sides = 9 cm

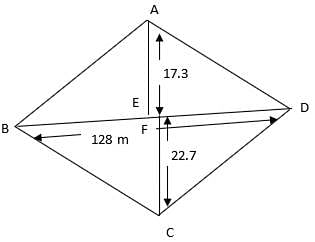
Q.20. In a four sided field, the length of the longer diagonal is 128 m. The lengths of perpendiculars from the opposite vertices upon this diagonal are 22.7 m and 17.3 m. Find the area of the field.

Given:
BD = 128 m
CF = 22.7 m
AE = 17.3 m

Now,
In ∆ABD,
Area of a triangle = 1/2 × base × height
= 1/2 × BD × AE
= 1/2 × 128 × 17.3
= 1107.2 m²
Similarly,
In ∆CBD,
Area of a triangle = 1/2 × base × height
= 1/2 × BD × FC
= 1/2 × 128 × 22.7
= 1452.8 m²
Now,
Area of field = ∆ABD + ∆CBD
= 1107.2 m² + 1452.8 m²
= 2560 m²