RS Aggarwal Solutions: Summative Assessment- 1 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download

Q.1. If the sum of the roots of the equation 3x2 – (3k – 2) x – (k – 6) = 0 is equal to the product of its roots then k = ?
(a) 1
(b) – 1
(c) 0
(d) 2

Let the roots of the given quadratic equation 3x² – (3k – 2)x – (k – 6)=0 be α and β.
Now,
sum of roots = α + β = (3k – 2)/3 and,
product of roots = αβ = – (k – 6)/3
[∵ If α and β are the roots of quadratic equation ax² + bx + c=0 then α + β = – b/a and αβ = c/a]
According to question –sum of roots = product of roots
∴ α + β = αβ
⇒ (3k – 2)/3 = – (k – 6)/3
⇒ 3k – 2 = – k + 6
⇒ 4k = 8
∴ k = 2
Hence, The value of k is 2.

Q.2. The number of all 2-digit numbers divisible by 6 is
(a) 12
(b) 15
(c) 16
(d) 18

All 2-digit numbers divisible by 6 are as follows: –
6, 12, ………., 96
The above series of numbers forms an arithmetic progression with first term(a) = 6 and, common difference(d) = (n + 1)th term – nth term = 12 – 6 = 6 last term or nth term(a_n) = 96
Let the number of terms in above series be n.
∵ a_n = a + (n – 1) × d
⇒ 96 = 6 + (n – 1) × 6
⇒ 90 = 6n – 6
⇒ 6n = 96
∴ n = 16
Thus, total no. of all 2-digit numbers divisible by 6.

Q.3. A fair die is thrown once. The Probability of getting a composite number is
(a) 1/3
(b) 1/6
(c) 2/3
(d) 0

Let P be the event of getting a composite number while throwing a dice.
Total no. of outcomes when n number of die are thrown = 6ⁿ
∴ no. of total outcomes = n(S) = 6
Sample Space = {1, 2, 3, 4, 5, 6} favourable elementary events = getting a composite number
= {4, 6}
∴ no. of favourable elementary events = n(P) = 2
Thus, the probability of getting a composite number = n(P)/n(S)
= 2/6
= 1/3

Q.4. Which of the following statements is true?
(a) The tangents drawn at the end points of a chord of a circle are parallel.
(b) From a point P in the exterior of a circle, only two secants can be drown through P to the circle.
(c) From a point P in the plane of a circle, two tangents can be drawn to the circle.
(d) The perpendicular at the point of contact to the tangent to a circle passes through the centre of the circle.

A Tangent is a line that intersects a circle at exactly one point.
The tangents drawn at the end points of a chord of a circle can be parallel only if that chord is the diameter of the circle. This will be clear from the fig.1 and fig.2 shown below.

Thus, statement (a) is incorrect.
A secant is a segment that intersects a circle twice.
From a point P in the exterior of a circle, infinite no. of secants can be drown through P to the circle. This can be shown in the fig.3 drawn below.

Thus, statement (b) is incorrect.
A Tangent is a line that intersects a circle at exactly one point.
From a point P in the plane of a circle, two tangents can be drawn to the circle only if point P is exterior to the circle. This can be shown in the fig.4 drawn below.

Thus, statement (c) is incorrect.

In the above fig.5, we take a point Q on the tangent XY to the circle with centre O. Obviously, this point Q should lie outside to the circle otherwise XY will become secant. And, P is the point of contact. Clearly,
OQ > OP
Also, this is also true for all the points lying on the tangent XY except point P. And,
we know that perpendicular distance is always the shortest distance.
OP is shortest of all the distances b/w points O and any other points on XY i.e.
OP ⊥ XY
Hence, The perpendicular at the point of contact to the tangent to a circle passes through the centre of the circle.
Thus, statement (d) is correct.

Q.5. In the given figure, PA and PB are tangents to a circle such that PA = 8 cm and ∠ APB = 60˚. The length of the chord AB is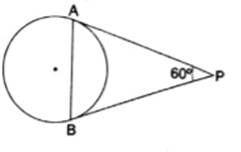

(a) 8 cm
(b) 10 cm
(c) 12 cm
(d) 6 cm

In Δ PAB,
∠ APB = 60° and PA = 8 cm [given]
∴ PB = PA = 8 cm
[∵ tangents drawn from an exterior point to the circle are equal in length]
⇒ ∠ PAB = ∠ PBA = θ [LET]
Now, In Δ PAB
∠ APB + ∠ PAB + ∠ PBA = 180° [∵ Sum of all the angles of a Δ is 180°]
⇒ 60° + θ + θ = 180°
⇒ 60° + 2θ = 180°
⇒ 2θ = 120°
∴ θ = 60°
Thus, Δ PAB is an equilateral Triangle.
∴ Length of chord AB = 8 cm.

Q.6. The angle of depression of an object from a 60-m-high tower is 30˚. The Distance of the object from the tower is
(a) 20√ 3 m
(b) 60√ 3 m
(c) 40√ 3 m
(d) 120 m

Let the Distance of the object from the tower be x meters.
∴ BC = x m
Given –
height of tower = AB = 60 m
Angle of depression = ∠ DAC = 30°
∴ ∠ BCA = ∠ DAC = 30°
[∵ When two‖lines are intersected by a third line then theAlternate interior angles will be equal.]
Now, In Δ ABC
tan 30° = AB/BC = 60/x [∵ tan θ = perpendicular/base]
⇒ 1/√3 = 60/x
∴ x = 60√3 meters

Q.7. In what ratio does the point P (2, – 5) divide the line segment joining A (– 3,5) and B(4, – 9)?
(a) 3:2
(b) 2:1
(c) 5:2
(d) 5:3

Let the point P (2, – 5) divide the line segment joining A (– 3,5) and B(4, – 9) in the ratio m:n.
Let (x,y) ≡ (2, – 5)
(x₁,y₁) ≡ (– 3,5)
and (x₂,y₂) ≡ (4, – 9)
Using Section Formula,


⇒ 2 × (m + n) = 4m – 3n
⇒ 2m + 2n = 4m – 3n
⇒ 5n = 2m
∴ m:n = 5:2
Since the ratio is positive, Point P divides the line segment AB internally in the ratio 5:2.

Q.8. Three solid spheres of radii 6 cm, 8 cm and 10 cm are melted to form a sphere. The radius of the sphere so formed is
(a) 24cm
(b) 16 cm
(c) 14 cm
(d) 12 cm

Let the radius of the sphere so formed be r cm.
Given –
Radius of 1st sphere(r₁) = 6 cm
Radius of 2nd sphere(r₂) = 8 cm
Radius of 3rd sphere(r₃) = 10 cm
After Melting all these spheres, the volume will remain unchaged.
∴ Vol. of 1st sphere + Vol. of 2nd sphere + Vol. of 3rd sphere
= Vol. of new sphere so formed
⇒ (4/3)π(r₁)³ + (4/3)π(r₂)³ + (4/3)π(r₃)³ = (4/3)π(r)³
Taking out (4/3)π from both sides, we get –
⇒ (r₁)³ + (r₂)³ + (r₃)³ = (r)³
⇒ (6)³ + (8)³ + (10)³ = (r)³
⇒ 216 + 512 + 1000 = (r)³
⇒ (r)³ = 1728
∴ r = 12 cm
Thus, the radius of new sphere is 12 cm.

Q.9. Find the value of p for which the quadratic equation x² – 2px + 1 = 0 has no real roots.

The given quadratic equation is x² – 2px + 1 = 0.
And, Discriminant D of the quadratic equation ax² + bx + c = 0 is given by –
D = b² – 4ac
Comparing the equation ax² + bx + c = 0 with given quadratic equation is x² – 2px + 1 = 0, we get –
a = 1, b = – 2p and, c = 1
∴ D = (– 2p)² – 4(1)(1) = 4p² – 4 = 4(p² – 1)
For no real roots,
D < 0
⇒ 4(p² – 1) < 0
⇒ p² – 1 < 0
⇒ (p + 1)(p – 1) < 0
∴ p ∈ (– 1,1)
Thus, p can take any values between – 1 and 1 for no real roots of given quadratic equation.

Q.10. Find the 10th term form the end of the AP 4, 9, 14, .. , 254.

The above series of numbers forms an arithmetic progression with first term(a) = 4 and, common difference(d) = (n + 1)th term – nth term = 9 – 4 = 5 last term or nth term(a_n) = 254
Let the total no. of terms in above A.P be n.
∴ a_n = a + (n – 1) × d
⇒ 254 = 4 + (n – 1) × 5
⇒ 250 = 5n – 5
⇒ 5n = 255
∴ n = 51
∴ 10th term from the end of AP = 51 – 10 + 1 = 42th term from the beginning
∴ 42th term = a₄₂ = a + (42 – 1)d
= 4 + 41 × 5
= 209
Hence, 10th term from the end of AP is 209.

Q.11. Which term of the AP 24, 21 ,18, 15, … is the first negative term?

Let the nth term of the AP be the first negative term.
In the given AP –first term(a) = 24 and, common difference(d) = (n + 1)th term – nth term = 21 – 24 = – 3
According to question –
∴ a_n < 0
⇒ a + (n – 1) × d < 0
⇒ 24 + (n – 1) × (– 3) < 0
⇒ – 3n + 27 < 0
⇒ 3n > 27
∴ n > 9
Thus, the first negative term of given AP is 10th term.

Q.12. A circle is touching the side BC of a Δ ABC at P and is touching AB and AC when produced at Q and R respectively.
Prove that AQ = 1/2 (perimeter of Δ ABC).

In the given figure,
AQ and AR are two tangents drawn from an exterior point A at contact points Q and R on the circle.
∴ AQ = AR
⇒ AQ = AC + CR…..(1)
Similarly,
BQ and BP are two tangents drawn from an exterior point B at contact points Q and P on the circle.
∴ BQ = BP…..(2)
And,
CR and CP are two tangents drawn from an exterior point C at contact points R and P on the circle.
∴ CR = CP…..(3)
Now, Equation (1) can be written as –
AQ = (AC + CR + AC + CR)/2
⇒ AQ = (AC + CP + AC + CR)/2 [using(3)]
⇒ AQ = (AC + CP + AR)/2
⇒ AQ = (AC + CP + AQ)/2
⇒ AQ = (AC + CP + AB + BQ)/2
⇒ AQ = (AC + CP + AB + BP)/2 [using(2)]
⇒ AQ = (AB + BC + AC)/2 [∵BP + CP=BC]
Thus, AQ = (1/2) × perimeter of Δ ABC

Q.13. Two vertical of a ΔABC are given by A(6, 4) and B (– 2, 2) and its centroid is G(3, 4). Find the coordinates of its third vertex C.

Let the third vertex C ≡ (x₃, y₃)
In a Δ ABC,
Vertex A ≡ (x₁, y₁) ≡ (6, 4)
Vertex B ≡ (x₂, y₂) ≡ (– 2, 2)
Centroid(G) ≡ (x, y) ≡ (3,4)
Centroid of a Δ ABC is given by –
x = (x₁ + x₂ + x₃)/3
⇒ 3 = (6 – 2 + x₃)/3
⇒ 9 = 4 + x₃
∴ x₃ = 5
And,
y = (y₁ + y₂ + y₃)/3
⇒ 4 = (4 + 2 + y₃)/3
⇒ 12 = 6 + y₃
∴ y₃ = 6
Thus, the coordinates of third vertex C is (5, 6).

Q.14. A box contain 150 orange is taken out from the box at random and the probability of its being rotten is 0.06 then find the number of good orange in the box.

Total no. of Oranges = 150
Probability of rotten oranges =0.06
∴ Probability of good oranges = 1 – 0.06 = 0.94
⇒ (no. of good oranges)/(no. of total oranges) = 0.94
⇒ no. of good oranges = 0.94 × 150 = 141
Thus, the number of good orange in the box = 141

Q.15. A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.

fig.10
Given –
Total Height of cone = 31 cm
Radius of hemisphere(r) = Base Radius of Cone
= Height of hemisphere
= 7 cm
∴ Height of cone(h) = 31 – 7 = 24 cm
Slant Height of Cone(l) = √(h² + r²) = √(24² + 7²) = 25 cm
Now,
Total Surface Area of the Toy
= Curved Surface Area of Cone + Curved Surface Area of Hemisphere
= πrl + 2πr²
= π(rl + 2r²)
= π(7 × 25 + 2 × (7)²)
= π(175 + 98)
= π(273)
= 3.14 × 273
= 857.22 cm²

Q.16. Solve: a²b²x² – (4b⁴ – 3a⁴) x – 12a²b² = 0.

The given quadratic equation is –
a²b²x² –(4b^{4 –} 3a⁴) x – 12a²b² = 0
Discriminant D of the quadratic equation ax² + bx + c = 0 is given by –
D = b² – 4ac
Comparing the equation ax² + bx + c = 0 with given quadratic equation is a²b²x² –(4b⁴ –3a⁴) x – 12a²b² = 0,we get –
a = a²b² , b = –(4b^{4 –} 3a⁴) and, c = – 12a²b²
∴ The roots of the given quadratic equation is given by –


Thus, the roots of the given quadratic equation are (4b²/a²) and (– 3a²/b²). 

Q.17. If the 8^th term of an AP is 31 and its 15^th term is 16 more than the 11^th term, find the AP.

Let the first term and common difference of given AP be a and d respectively.
According to question –8th term of AP = a₈ = 31 [Given]
⇒ a + (8 – 1)d = 31
⇒ a + 7d = 31…..(1)
15th term of AP = a₁₅ = 16 + a₁₁
⇒ a + (15 – 1)d = 16 + a + (11 – 1)d
⇒ 14d = 16 + 10d
⇒ 4d = 16
∴ d = 4
Substituting the value of d in equation(1), we get –
a = 31 – 7 × 4 = 31 – 28 = 3
Thus, the required AP is 3,7,11,15,…….

Q.18. Find the sum of all two-digit odd positive numbers.

All the two-digit odd positive numbers are –
11,13,15,17,……….,99
The above series of numbers forms an arithmetic progression with first term(a) = 11 and, common difference(d) = (n + 1)th term – nth term = 13 – 11 = 2
last term or nth term(a_n) = 99
Let the total no. of terms in above A.P be n.
∴ a_n = a + (n – 1) × d
⇒ 99 = 11 + (n – 1) × 2
⇒ 88 = 2n – 2
⇒ 2n = 90
∴ n = 45
Sum of all the 45 terms of the AP is given by –
S₄₅ =(45/2)(11 + 99)
[∵S_n = (n/2)(a + l) =(n/2)[(2a + (n – 1)d]
=(45/2) × 110
=45 × 55
=2475
Thus, the sum of all two-digit odd positive numbers = 2475.

Q.19. In the adjoining figure, PA and PB are tangents drawn from an external point P to a circle with centre O. Prove that ∠ APB = 2 ∠ OAB.

fig.11
Let ∠ APB = θ
In Δ APB,
PA = PB
[∵ Tangents drawn from an exterior point to the circle are equal in length]
⇒ Δ APB is an isoceles triangle.
∴ ∠ PAB = ∠ PBA = α [LET]
Now,
∠ APB + ∠ PAB + ∠ PBA = 180° [∵ sum of all the angles of Δ=180°]
⇒ θ + α + α = 180°
⇒ 2α = 180° – θ
∴ α = ∠ PAB = 90° – (θ/2)
Also, OA⊥AP
[∵ radius of a circle is always ⊥ to the tangent at the point of contact.]
∴ ∠ PAB + ∠ OAB = 90°
⇒ 90° – (θ/2) + ∠ OAB = 90°
⇒ ∠ OAB = (θ/2) = (1/2)∠ APB
∴ ∠ APB = 2 ∠ OAB
Hence, Proved.

Q.20. In the adjoining figure, quadrilateral ABCD is circumscribed. If the radius of the in circle with centre O is 10 cm and AD ⊥ DC, find the value of x.

In the given figure,
DS and DR are the two tangents drawn from an external point D at the point of contacts S and R respectively. And,
OS ⊥ DS and OR ⊥ DR
[∵ radius of a circle is always⊥to the tangent at the point of contact.]
⇒ OSDR is a square [∵ AD ⊥ DC (Given)]
∴ DR = 10 cm
Similarly,
BP and BQ are the two tangents drawn from an external point B at the point of contacts A and Q respectively.
∴ BP = BQ = 27 cm
[∵ Tangents drawn from an exterior point to the circle are equal in length]
⇒ QC = BC – BQ = 38 – 27 = 11 cm
Also, CR and CQ are the two tangents drawn from an external point C at the point of contacts R and Q respectively.
∴ CR = CQ = 11 cm
[∵ Tangents drawn from an exterior point to the circle are equal in length]
∴ DC = x = DR + CR = 10 + 11 = 21 cm.
Thus, the value of x is 21 cm.

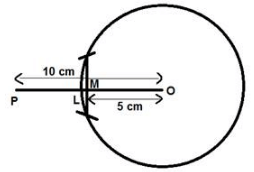
Q.21. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct a pair of tangents to the circle. Measure the length of each of the tangent segments.

Steps of Construction:
1. Draw a circle with centre O with radius OL and a point P outside it. Join PO and bisect it. Let M be the midpoint of PO.

fig.13
2. Taking M as centre and MO as radius, we will draw a circle.
Let it intersect the given circle at the points Q and R.

fig.14
3. Join PQ and PR.
Then PQ and PR are the required two tangents.

fig.15
4. Join OQ. Then ∠ PQO is an angle in the semicircle and,
∴ ∠ PQO = 90°

fig.16
Since, OQ is a radius of the given circle, PQ has to be a tangent to the circle.
Similarly,
PR is also a tangent to the circle.
After measuring the lenghts of tangents using scale, we find that both the tangents are equal in length which concludes that all the measurements and steps done correctly.
Length of Each Tangent = 8 cm

Q.22. The three vertices of a parallelogram ABCD, taken in order are A (1, – 2), B (3, 6) and C (5, 10). Find the coordinates of the fourth vertex D.

Let the coordinates of the fourth vertex D be (x₄, y₄).
We know that –
Diagonals of a∥gm bisect each other.
∴ Mid – point of diagonal AC ≡ Mid – point of diagonal BD

⇒ 6 = 3 + x₄ and 8 = 6 + y₄
⇒ x₄ = 3 and y₄ = 2
Thus, the coordinates of the fourth vertex D is (3,2).

Q.23. Find the third vertex of a Δ ABC if two of its vertices are B (– 3, 1) and C (0, – 2) and its centroid is at the origin.

Let the third vertex A ≡ (x₁,y₁)
In a Δ ABC,
Vertex B ≡ (x₂,y₂) ≡ (– 3,1)
Vertex C ≡ (x₃,y₃) ≡ (0, – 2)
Centroid(G) ≡ (x,y) ≡ (0,0)
Centroid of a Δ ABC is given by –
x = (x₁ + x₂ + x₃)/3
⇒ 0 = (x₁ – 3 + 0)/3
⇒ 0 = x₁ – 3
∴ x₁ = 3
And,
y = (y₁ + y₂ + y₃)/3
⇒ 0 = (y₁ + 1 – 2)/3
⇒ 0 = y₁ – 1
∴ y₁ = 1
Thus, the coordinates of third vertex A is (3,1).

Q.24. Cards marked with all 2-digit numbers are placed in a box and are mixed thoroughly. One card is drawn at random. Find the probability that the number on the card is
(a) divisible by 10
(b) a perfect square number
(c) a prime number less than 25

Sample Space = Cards marked with 2-digit numbers
= {10,11,12,……..,99)
No. of Sample Space = n(S) = 90
(a) Let P be the event of getting a card marked with 2-digit numbers which is divisible by 10.
∴ favourable elementary events = {10,20,30,…………,90}
no. of favourable elementary events = n(P) = 9
Thus, Probability of getting a card marked with number divisible by 10 = n(P)/n(S) = 9/90 = 1/10
(b) Let P be the event of getting a card marked with 2-digit square numbers.
∴ favourable elementary events = {16,25,36,…….,81}
no. of favourable elementary events = n(P) = 6
Thus, Probability of getting a card marked with number divisible by 10 = n(P)/n(S) = 6/90 = 1/15
(c) Let P be the event of getting a card marked with 2-digit prime numbers less than 25.
∴ favourable elementary events = {11,13,17,19,23}
no. of favourable elementary events = n(P) = 5
Thus, Probability of getting a card marked with number divisible by 10 = n(P)/n(S) = 5/90 = 1/18

Q.25. A road which is 7 m wide surrounds a circular park whose circumference is 352 m. Find the area of the road. [Take π = 22/7.]

fig.17
Let the radius of the circular park be r meters.
Given –
Circumference of circular park = 352 m
⇒ 2 × π × r = 352
⇒ 2 × (22/7) × r = 352
⇒ r = (7/44) × 352
∴ r = 7 × 8 = 56 m
⇒ outer radius = 56 + 7 = 63 m
∴ Area of the road = π(63² – 56²)
= (22/7)(63 + 56)(63 – 56)
= (22/7)(119)(7)
= 22 × 119
= 2618 m²

Q.26. A round table cover shown in the adjoining figure has six equal designs. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of ₹ 0.50 per cm². [Use √ 3 = 1.73.]

In the given figure, all the six desings covering equal area of the circle, therefore each design will subtend equal angles at the centre which is equal to (360°/6) i.e. 60°.
Also, the six triangles will be equal in area which is obtained by joining vertices of hexagon to the centre.
The triangle obtained will be equilateral because adjacent sides will be equal to the radius i.e. base angles will be equal and angle b/w them is 60° which concludes that other two angles will also be equal to 60° each.
∴ Area of six equilateral Δ = 6 × (√3/4) × (radius)²
= (3√3/2) × (28)²
= 1.5 × 1.73 × 784
= 2034.48 cm²
Area of Circle = π × (radius)² = (22/7) × (28)² = (22/7) × 784
= 22 × 112
= 2464 cm²
Area of the designs = Area of Circle – Area of six equilateral Δ
= (2464 – 2034.48) cm²
= 429.52 cm²
∴ Cost of making designs =Rs. (0.50 × 429.52) = Rs. 214.76

Q.27. In an equilateral triangle of side 12 cm, a circle is inscribed touching its sides. Find the area of the portion of the portion of the triangle not included in the circle. [Take √ 3 = 1.73 and π = 3.14.]

fig.19
Let the radius of the circle be r cm.
In the fig.19,
AR and AQ are making a pair of tangents drawn from vertex A of Δ ABC on the circle.
∴ AR = AQ = x [LET]
BR and BP are making a pair of tangents drawn from vertex B of Δ ABC on the circle.
∴ BR = BP = y [LET]
CP and CQ are making a pair of tangents drawn from vertex C of Δ ABC on the circle.
∴ CP = CQ = z [LET]
Given –
Δ ABC is an equilateral triangle.
∴ AB = BC = AC = 12 cm
⇒ AR + BR = BP + CP = AQ + CQ = 12
⇒ x + y = y + z = x + z = 12…..(1)
Now,
(x + y + y + z + x + z) = (12 + 12 + 12)
⇒ 2 × (x + y + z) = 36
⇒ x + y + z = 18…..(2)
Subtracting equation(1) from equation(2), we get –
x = y = z = 6 cm
Also, the line joining the centre the circle to the vertices of Δ which circumscribes the circle bisects the angles of a Δ.
∴ ∠ OBP = 30°
In Δ BOP,
tan ∠ OBP = OP/BP = r/6
⇒ tan 30° = r/6
⇒ 1/√3 = r/6
∴ r = 6/√3 = 2√3 = 3.46 cm
Area of Δ ABC = (√3/4) × (side)²
=(1.73/4) × (12)²
= 1.73 × 36
= 62.28 cm²
Area of circle = π × (radius)²
= 3.14 × (3.46)²
= 37.59 cm²
Thus, Area of the triangle which is not included in the circle
= Area of Δ ABC – Area of circle
= (62.28 – 37.59) cm²
= 24.69 cm²

Q.28. If a sphere has the same surface area as the total surface area of a circular cone of height 40 cm and radius 30 cm, find the radius of the sphere.

Let the radius of the sphere be r cm.
Given –
Height of cone(h) = 40 cm
Radius of cone(r) = 30 cm
∴ Slant height of cone(l) = √(h² + r²) = √(40² + 30²) = 50 cm
According to question –
Surface Area of Sphere = Total Surface Area of Circular Cone
⇒ 4 × π × r² = π × r × (r + l)
⇒ 4r = r + l
⇒ 3r = l
∴ r = (l/3) = (50/3) cm
Thus, the radius of the Sphere = (50/3) cm.

Q.29. A two–digit number is such that the product of its digits is 35. If 18 is added to the number, the digit interchange their places. Find the number.

Let the two-digit number be xy(i.e. 10x + y).
After reversing the digits of the number xy, the new number becomes yx (i.e. 10y + x).
According to question –
xy = 35…..(1)
And,
(10x + y) + 18 = (10y + x)
⇒ 9x – 9y = – 18
⇒ x – y = – 2…..(2)
From equation(2), we get –
x = y – 2…..(3)
Substitute the value of x in equation(1), we get –
y(y – 2) = 35
⇒ y² – 2y – 35 = 0
⇒ y² – 7y + 5y – 35 = 0
⇒ y(y – 7) + 5(y – 7) = 0
⇒ (y – 7)(y + 5) = 0
∴ y = 7 [∵ y = – 5 is invalid because digit of a number can't be – ve.]
Substituting the value of y in equation (3), we get –
x = 5
Thus, the required number is 57.

Q.30. Two water taps together can fill a tank in 9(3/8) hours. The larger tap takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.

Let the tap of the smaller diameter and larger diameter fills the tank alone in x and (x – 10) hours respectively.
In 1 hour, the tap of the smaller diameter can fill 1/x part of the tank.
In 1 hour, the tap of the larger diameter can fill 1/(x – 10) part of the tank.
Two water taps together can fill a tank in 9(3/8) hours = 75/ 8 hours.
But in 1 hour the taps fill 8/75 part of the tank.

⇒
⇒
⇒ 4x² – 40x = 75x – 375
⇒ 4x² – 115x + 375 = 0
⇒ 4x² – 100x – 15x + 375 = 0
⇒ 4x(x – 25) – 15( x – 25) = 0
⇒ (4x -15)( x – 25) = 0
⇒ x = 25, 15/4
Taking x = 15 / 4
⇒ x – 10 = -25 /4 (But, time cannot be negative)
Now, taking x = 25
⇒ x – 10 = 15
Larger diameter of the tap can the tank 15 hours and smaller diameter of the tank can fill the tank in 25 hours.

Q.31. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact to the centre.

fig.20
In the fig.20, PA and PB are the two tangents drawn from an external point P at the point of contacts A and B on the circle with centre O respectively.
∴ OA ⊥ PA and OB ⊥ PB
[∵ radius of a circle is always⊥to the tangent at the point of contact.]
∴ ∠ OAP = ∠ OBP = 90°
we know that –
Sum of all the angles of a quadrilateral = 360°
In quadrilateral OAPB,
∠ OAP + ∠ OBP + ∠ APB + ∠ AOB = 360°
⇒ 180° + ∠ APB + ∠ AOB = 360°
∴ ∠ APB + ∠ AOB = 180°
Hence, the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact to the centre.

Q.32. From the top of a 7 – m high building, the angle of elevation of the top of a cable tower is 60˚ and the angle of depression of its foot is 45˚. Find the height of the tower. [Given √ 3 = 1.73.]

fig.21
Given –
Angle of Elevation = ∠ EAC = 60°
Angle of Depression = ∠ EAD = ∠ BDA = 45°
Height of Building = AB = ED = 7 m
In Δ ABD,
tan 45° = AB/BD
⇒ 1 = 7/BD
⇒ BD = 7 m
∴ AE = BD = 7 m [from fig.21]
And, In Δ ACE
tan ∠ CAE = CE/AE
⇒ tan 60° = CE/7
⇒ √3 = CE/7
⇒ CE = 7√3 m
Thus, Height of Tower = CE + ED = 7√3 + 7
= 7(1.73 + 1)
= 7 × 2.73
= 19.11 m

Q.33. Puja works in a bank and she gets a monthly salary of ₹ 35000 with annual increment of ₹ 1500. What would be her monthly salary in the 10^th year?

Given –
Monthly Salary = Rs. 35000
∴ Annual Salary = Rs. (12 × 35000) = Rs. 420000
Annual Increment = Rs. 1500
Let us consider this situation as an AP with first term = a = Rs. 420000 and, Common Difference = d = Rs. 1500
∴ Salary in 10th year is given by –
a₁₀ = a + (10 – 1)d = 420000 + 9 × 1500 = Rs. 433500
Thus, Monthly Salary in 10th year = Rs. (433500/12)
= Rs. 36125

Q.34. In the given figure ABCD represent the quadrant of a circle of radius 7 cm with centre A. Calculate the area of the shaded region. [Take π = 22/7.]

Area of quadrant CAB = (π/4) × (radius)²
= (22/28) × (7)²
= 37.5 cm²
Area of Δ EAB = (1/2) × base × height
= (1/2) × 7 × 2
= 7 cm²
Thus, Area of shaded Region
= Area of quadrant CAB – Area of Δ EAB
= (37.5 – 7) cm²
= 30.5 cm²

Q.35. The radii of the circular end of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its capacity and total surface area. [Take π = 22/7.]

fig.23
Given –
MC = 27 cm, NE = 33 cm and CE = 10 cm
Let AM = h cm, AN = H cm and AC = l cm
∴ AE = AC + CE = (l + 10) cm
In the above fig.19,
Δ AMC and Δ ANE are similar triangles because their corresponding angles are equal.

…..(1)
On cross multiplying last two fractional parts of equation(1), we get –
33l = 27l + 270
⇒ 6l = 270
∴ l = 45 cm
∴ AE = 45 + 10 = 55 cm
In Δ ANE,
AN² + NE² = AE² [by using pythagoras theorem]
⇒ H² + (33)² = (55)²
⇒ H² + 1089 = 3025
⇒ H² = 1936
∴ H = 44 cm
From first and last fractional parts of equation(1), we get –
h = (27/33) × 44 = 36 cm
∴ Height of frustum = H – h = 44 – 36 = 8 cm
Now,
Capacity of Frustum = Vol. of Cone ADE – Vol. of cone ABC
= (1/3)π × (NE)² × (AN) – (1/3)π × (MC)² × (AM)
= (1/3)π × [(33)² × (44) – (27)² × (36)]
= (22/21) × [47916 – 26244]
= (22/21) × 21672
= 22 × 1032
= 22704 cm³
Total Surface Area of Frustum
= Area of Curved Part(Trapezium)+ Area of Upper Circular Part+ Area of lower Circular Part
= [(1/2) × (sum of parallel sides) × (height of frustum)] + [π × (MC)²] + [π × (NE)²]
= [(1/2) × 2π(27 + 33) × 8] + [(22/7) × (27)²] + [(22/7) × (33)²]
= 480(22/7) + (22/7) × [(27)² + (33)²]
= 480(22/7) + (22/7) × 1818
= (22/7) × 2298
= 22 × 328.28
= 7222.16 cm²
Thus, Capacity of Frustum = 22704 cm³ and, Total Surface Area of Frustum = 7222.16 cm²

Q.36. From an external point p, tangents PA and PB are drawn to a circle with centre O. If CD is the tangent to the circle at the point E and PA = 14 cm, find the perimeter of ΔPCD.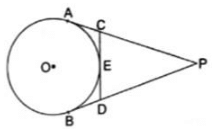

In the given fig.,
CA and CE are the two tangents drawn from an external point C at the point of contacts A and E respectively.
∴ CA = CE
[∵ Tangents drawn from an exterior point to the circle are equal in length]
Similarly, DE and DB are the two tangents drawn from an external point D at the point of contacts E and B respectively.
∴ DE = DB
[∵ Tangents drawn from an exterior point to the circle are equal in length]
Perimeter of Δ PCD = PC + CD + PD
= PC + CE + DE + PD
= PC + CA + BD + PD
= PA + PB [∵ PA = PC + CA and PB = PD + BD]
= 14 + 14 [∵ PA=PB]
= 28 cm

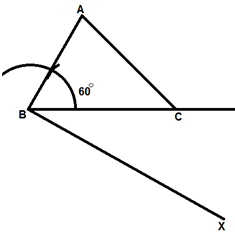
Q.37. Construct a ΔABC in which BC = 5.4 cm, AB = 4.5 cm and ∠ ABC = 60˚.
Construct a triangle similar to this triangle, whose side are 3/4 of the corresponding sides of ΔABC.

Steps of Construction :
1. Draw a line Segment BC = 5.4 cm and draw an angle of 60° at point B and mark a length of AB = 4.5 cm on the line passing through B. Then join AC.

fig.25
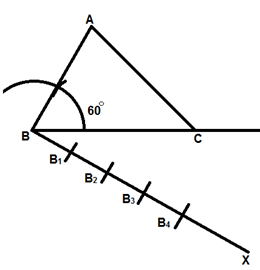
2. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.

fig.26
3. Locate 4 points [the greater of 4 and 3 in (3/4)] B₁, B₂, B₃, B₄ on BX so that
BB₁ = B₁B₂ = B₂B₃ = B₃B₄

fig.27
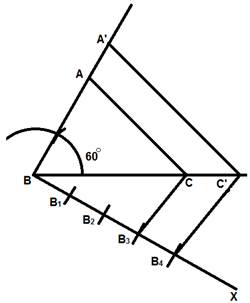
4. Join B₃ [the 3rd point, 3 being smaller of 3 and 4 in (3/4)] to C and draw a line through B₄ parallel to B₃C, intersecting the extended line segment BC at C′.

fig.28
5. Draw a line through C′ parallel to CA intersecting the extended line segment BA at A′.

fig.29
Then A′BC′ is the required triangle.

Q.38. A bag contain 5 red balls and some blue balls. If the probability of drawing a blue ball from the bag is thrice that of a red ball, find the number of blue balls in the bag.

Let the no. of blue balls in the bag be x.
Let B and R be the event of drawing a blue and red ball respectively.
∴ total no. of balls in the bag = x + 5
According to question –
Probability of drawing blue ball
= 3 × Probability of drawing blue ball
⇒ [no. of blue balls/total no. of balls]
= 3 × [no. of red balls/total no. of balls]
⇒ (x/x + 5) =3 × (5/x + 5)
∴ x = 15
Thus, the no. of blue balls in the bag is 15.

Q.39. In what ratio is the line segment joining the points (– 2, – 3) and (3, 7) divided by the y-axis? Also, find the coordinates of the point of division.

Let the point on the y-axis which divides the line segment joining the points A(– 2, – 3) and B(3, 7) be C(0,y).
Let the ratio in which y-axis divides AB line segment be m:n.
Let (x,y) ≡ (0,y)
(x₁,y₁) ≡ (– 2, – 3)
and (x₂,y₂) ≡ (3,7)
Using Section Formula,


⇒ 3m = 2n
∴ m:n = 2:3
Now,


⇒ y = (5/5) = 1
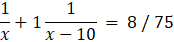
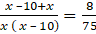
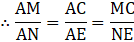
Thus, the line segment joining the points (– 2, – 3) and (3, 7) divided by the y-axis in the ratio 2:3 internally and the coordinates of the point of division is (0, 1).