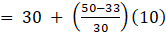RS Aggarwal Solutions: Summative Assessment- 1 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
Sample Paper: I
Q.1. Euclid's Division Lemma states that for any two positive integers a and b, there exist unique integers q and r such that a = bq + r, where
(a) 0 < r < b
(b) 0 ≤ r < b
(c) 0 < r ≤ b
(d) 1<r< b
Euclid's division lemma :
Given positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 ≤ r < b
Q.2. In the given figure, the graph of the polynomial p(x) is shown. The number of zeros of p(x) is
(a) 1
(b) 3
(c) 2
(d) 4
The zeroes of polynomial means that value of polynomial becomes zero.
In the above graph, the curve depicts the polynomial and it gets zero at two points, therefore p(x) has two zeroes.
Q.3. In ΔABC, it is given that DE || BC. If AD = 3 cm, DB = 2 cm and DE = 6 cm, then BC = ?
(a) 9 cm
(b) 10 cm
(c) 12 cm
(d) 18 cm
In ΔADE and ΔABC
∠ADE = ∠ABC [Corresponding angles as DE || BC]
∠AED = ∠ACB [Corresponding angles as DE || BC]
ΔADE ~ ΔABC [By Angle-Angle Similarity criterion][Corresponding sides of similar triangles are in the same ratio]
Now,
Given, AD = 3 cm
DB = 2 cm
DE = 6 cm
⇒ AB = AD + DB = 3 + 2 = 5 cm
Using this in above equation,
⇒ BC = 10 cm
Q.4. If sin 3θ = cos (θ - 2°), where 3θ and (θ - 2°) are both acute angles, then θ = ?
(a) 44°
(b) 22°
(c) 46°
(d) 23°
Given, we know that
sin θ = cos(90° - θ)
Replacing θ by 3θ
⇒ sin(3θ) = cos(90° - 3θ)
⇒ cos(θ - 2°) = cos(90° - 3θ)
[ Given, sin 3θ = cos(θ - 2°)]
⇒ θ - 2° = 90° - 3θ
⇒ 4θ = 92°
⇒ θ = 23°
Q.5. If tan θ = √3, then 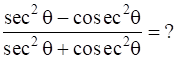
(a) -1
(b) 1
(c) -1/2
(d) 1/2
Given,
tan θ = √3
⇒ tan2θ = 3
⇒ sec2θ - 1 = 3 [As tan2θ + 1 = sec2θ]
⇒ sec2θ = 4 …[1]
Also,
⇒as tanθ = √3
Squaring both sides,[As cot2θ + 1 = cosec2θ]
…[2]
Putting the values from [1] and [2] into given eqn
Q.6. The decimal expansion of 49/40 will terminate after how many places of decimal?
(a) 1
(b) 2
(c) 3
(d) will not terminate
We know that if p/q is a rational number, such that p and q are co-prime and q has factors in the form of 2m.5n, then, decimal expansion of p/q will terminate after the highest power of 2 or 5 (whichever is greater).
Therefore, 49/40 will terminate after 3 places of decimal.
Q.7. The pair of linear equations 6x - 3y + 10 = 0, 2x - y + 9 = 0 has
(a) one solution
(b) two solutions
(c) many solutions
(d) no solution
Comparing the equation with the set of equations
a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0
we have,
a1 = 6, a2 = 2
b1 = -3, b2 = -1
c1 = 10, c2 = 9
and we have,and
and
So, we have
and in this case, we know that equations have no solution.
Q.8. For a given data with 60 observations the 'less than ogive' and the 'more than ogive' intersect at (18.5, 30). The median of the data is
(a) 18
(b) 30
(c) 60
(d) 18.5
As we know that, the x-coordinate of the point of intersection of the more than ogive and less than ogive give us a median of the data.
So, the median of the data is 18.5.
Q.9. Is (7 x 5 x 3 X 2 + 3) a composite number? Justify your answer.
(7 x 5 x 3 x 2 + 3) = (210 + 3) = 213
And 213 = 71 x 3
As, this number is expressible as product of two no's other, the given number is composite.
[Composition no's are those no's which has factors other than 1 and itself]
Q.10. When a polynomial p(x) is divided by (2x + 1), is it possible to have (x - 1) as a remainder? Justify your answer.
No, because degree of remainder cannot be equal to the degree of divisor
And in this case degree of divisor, i.e. 2x + 1 = 1
And degree of remainder, i.e. x -1 = 1 is equal.
Q.11. If 3 cos2θ + 7sin2θ = 4, show that cotθ = √3
Given,
3cos2θ + 7sin2θ = 4
⇒ 3cos2θ + 3sin2θ + 4sin2θ = 4
⇒ 3(cos2θ + sin2θ) + 4sin2θ = 4
⇒ 3 + 4sin2θ = 4
[as sin2θ + cos2θ = 1]
⇒ 4sin2θ = 1
⇒ sin2θ = 1/4
⇒ sinθ = 1/2
⇒ θ = 30°
[as sinθ = 1/2]
⇒ cot θ = √3
[ as cot 30° = √3]
Q.12. If tan θ = 8/15 evaluate 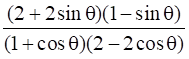
Now, To find :
[As, (a + b)(a - b) = a2 - b2]
[As sin2θ + cos2θ = 1]
Q.13. In the given figure, DE|| AC and DF || AE.
Prove that: 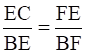
DE || AC [Given]
And we know, By Basic Proportional Theorem
If a line is drawn parallel to the one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in same ratio…[1]
And DF || AE
By Basic Proportional Theorem,[From [1]]
Hence, Proved
Q.14. In the given figure, AD ⊥ BC and BD = 1/3 CD. Prove that: 2CA2 = 2AB2 + BC2. 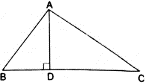
We have,
BC = BD + CD[1]
As, AD ⏊ BC
⇒ ΔADC is a right-angled triangle
By Pythagoras theorem,[i.e. hypotenuse2 = perpendicular2 + base2]
AD2 + CD2= CA2
⇒ AD2 = CA2 - CD2 ….[2]
Also, ΔABD is a right-angled triangle
By Pythagoras theorem,
AD2 + BD2 = AB2
From [2]
CA2 - CD2 + BD2 = AB2
⇒[From [1]]
⇒ 2CA2 - BC2 = 2AB2
⇒ 2CA2 = 2AB2 + BC2
Hence, Proved.
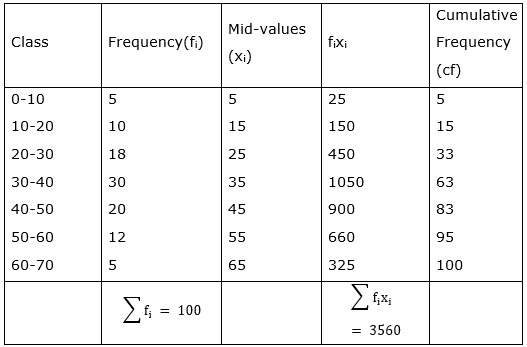
Q.15. Find the mode of the following distribution of marks obtained by 80 students: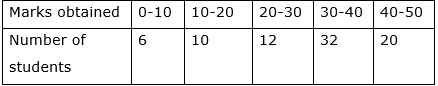
In the given data,
The maximum class frequency is 32. So, the modal class is 30-40.
Lower limit(l) of modal class = 30
Class size(h) = 40 - 30 = 10
Frequency(f1) of modal class = 32
Frequency(f0) of class preceding the modal class = 12
Frequency(f2) of class succeeding the modal class = 20
And we know,
Substituting values, we get
Q.16. Show that any positive odd integer is of the form (4q + 1) or (4q + 3), where q is a positive integer.
Let a be an positive odd integer, and let b = 4
By, using Euclid's division lemma,
a = 4q + r, where r is an integer such that, 0 ≤ r < 4
So, only four cases are possible
a = 4q or
a = 4q + 1 or
a = 4q + 2 or
a = 4q + 3
But 4q and 4q + 2 are divisible by 2, therefore these cases are not possible, as a is an odd integer.
Therefore,
a = 4q + 1 or a = 4q + 3.
Q.17. Prove that (5 - √3) is irrational.
Let 5 - √3 be rational,
Then, 5 - √3 can be expressed as p/q where, p and q are co-prime integers and q ≠ 0,
we have,
As p and q are integers, 5q - p is also an integeris a rational number.
But √3 is an irrational number, so the equality is not possible.
This contradicts our assumption, that 5 - √3 is a rational number.
Therefore, 5 - √3 is an irrational number.
Q.18. Prove that  is irrational.
is irrational.
Let
be rational,
Then,can be expressed as
where p and q are co-prime integers and
q ≠ 0,
we have,
As p and q are integers, 5p and 3q are also integersis a rational number.
But √3 is an irrational number, so the equality is not possible.
This contradicts our assumption, thatis a rational number.
Therefore,is an irrational number.
Q.19. A man can row a boat at the rate of 4 km/hour in still water. He takes thrice as much time in going 30 km upstream as in going 30 km downstream. Find the speed of the stream.
Speed of boat in still water = 4 km/h
Let the speed of stream be 'x'
Therefore,
Speed of the boat upstream = Speed of boat in still water - Speed of stream = 4 - x
Speed of the boat downstream = Speed of boat in still water + Speed of stream = 4 + x
Time taken to go upstream
Time taken to go downstream
Given, time taken in upstream is thrice as in downstream
⇒ 4 + x = 12 - 3x
⇒ 4x = 8
⇒ x = 2
i.e. the speed of stream = x is 2 km/hour.
Q.20. In a competitive examination, 5 marks are awarded for each correct answer, while 2 marks are deducted for each wrong answer. Jayant answered 120 questions and got 348 marks. How many questions did he answer correctly?
Let the number of correct answers = x
Let the number of wrong answers = y
Total no of questions attempted = x + y = 120
⇒ y = 120 - x ….[1]
Marks for each correct answer = 5
Marks for x correct answers = 5x
As 2 marks are deducted for each wrong question,
Marks deducted for y wrong answers = 2y
Total marks obtained by student will be 5x - 2y,
⇒ 5x - 2y = 348
⇒ 5x - 2(120 - x) = 348
⇒ 5x - 240 + 2x = 348
⇒ 7x = 588
⇒ x = 84
Hence, no of correct answers = x = 84
Q.21. If α and β are the zeros of the polynomial 2x2 + x - 6, then form a quadratic equation whose zeros are 2α and 2β.
We know that, for a quadratic equation ax2 + box + c
Sum of zeroes
Product of zeroes
Given equation = 2x2 + x - 6 and zeroes are α and β
Therefore,….[1] and
….[2]
Now, any quadratic equation having α and β as zeroes will have the form
p(x) = x2 - (α + β)x + αβ
⇒ equation having α and β as zeroes will have the form
p(x) = x2 - (2α + 2β)x + (2α)(2β)
⇒ p(x) = x2 - 2(α + β)x + 4αβ
From [1] and [2]
Hence required equation is x2 + x - 12.
Q.22. Prove that: (cosecθ - sinθ)(secθ - cosθ) = 
Taking L.H.S
= (cosecθ - sinθ)(secθ - cosθ)
We know, sin2θ + cos2θ = 1
Therefore,
Taking R.H.S[as sin2θ + cos2θ = 1]
LHS = RHS
Hence, Proved.
Q.23. If cosθ + sinθ = √2 cosθ, prove that cos θ - sinθ = √2 sinθ.
Given,
cos θ + sin θ = √2 cos θ …[1]
Squaring both side,
(cos θ + sin θ)2 = 2 cos2θ
⇒ cos2θ + sin2θ + 2cosθsinθ = 2cos2θ
⇒ 2cosθsinθ = 2cos2θ - cos2θ - sin2θ
⇒ 2cosθsinθ = cos2θ - sin2θ
⇒ 2cosθsinθ = (cosθ - sinθ)(cosθ + sinθ)
⇒ 2cosθsinθ = (cosθ - sinθ)( √2 cosθ) [From [1]]
Hence, Proved.
Q.24. ΔABC and ΔDBC are on the same base BC and on opposite sides of BC. If O is the point of intersection of BC and AD, prove that:
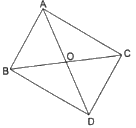
Given: ΔABC and ΔDBC with common base BC.
To Prove:
Construction: Draw AM ⏊ BC and DN ⏊ BC
Proof:
In ΔAMO and ΔDNO
∠AOM = ∠DON [Vertically opposite angle]
∠AMO = ∠DNO [Both 90°]
ΔAMO ~ ΔDNO [By Angle-Angle sum criterion][Corresponding sides of similar triangles are in the same ratio] [1]
Now, we know that
Area of a triangle
Therefore,[From [1]]
Hence, Proved
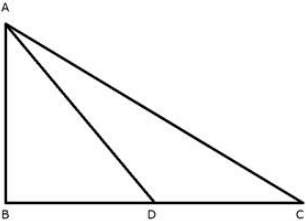
Q.25. In Δ ABC, the AD is a median and E is the midpoint of the AD. If BE is produced to meet 1 AC in F, show that AF = 1/3 AC.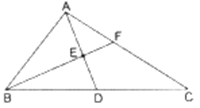
Proof:
Given: In ΔABC, the AD is a median and E is mid-point of the AD and BE is produced to meet AC in F.
To Prove:
Construction: Draw DG || BF as shown in figure
Proof:
Now, In ΔBFC
DG || BF [By construction]
As AD is a median on BC, D is a mid-point of BC
Therefore,
G is a mid-point of CF [By mid-point theorem]
⇒ CG = FG …[1]
Now, In ΔADG
EF || DG [By Construction]
As E is a mid-point of AD [Given]
Therefore,
F is a mid-point of AG [By mid-point theorem]
⇒ FG = AF …[2]
From [1] and [2]
AF = CG = FG …[3]
And
AC = AF + FG + CG
⇒ AC = AF + AF + AF [From 3]
⇒ AC = 3AF
Hence Proved.
Q.26. Find the mean of the following frequency distribution using step deviation method: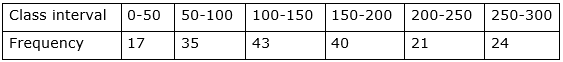
Let us first calculate the mid-values(xi) for each class-interval, By using the formula
Let us assume the assumed mean(a) = 75
and from that, we get the data as shown in above table.
And we know, By step-deviation method
Where, a = assumed mean
h = class size
Q.27. The mean of the following frequency distribution is 24. Find the value of p.
Let us first calculate the mid-values(xi) for each class-interval, By using the formula
By which, we get the following data
We know, that
Given, mean = 24
⇒ 1920 + 24p = 1700 + 35p
⇒ 11p = 220
⇒ p = 20
Q.28. Find the median of the following data:
First, let us make a cumulative frequency distribution of less than type.
In this case,
Sum of all frequencies, n = 53
Now, we know the median class is whose cumulative frequency is greater than and nearest to.
As, a Cumulative frequency greater than and nearest to 26.5 is 29, the median class is 60 - 70.
Median
where l = lower limit of median class,
n = number of observations,
cf = cumulative frequency of class preceding the median class,
f = frequency of median class,
h = class size
In this case,
l = 60
n = 53
cf = 22
f = 7
h = 10
Putting values, we get,
Median = 60 + ((26.5-22)/7)(10)= 60 + (45/7) = 66.4
Q.29. Let p(x) = 2x4 - 3x3 - 5x2 + 9x - 3 and two of its zeros are √3 and -√3. Find the other two zeros.
Two zeroes are √3 and -√3,
Therefore (x -√3)(x - (-√3) = (x - √3)(x + √3) is a factor of p(x).
Let us divide p(x) by (x - √3)(x + √3) = (x2 - 3)
⇒ (2x4 - 3x3 - 5x2 + 9x - 3) = (x2 - 3)(2x2 - 3x + 1)
= (x - √3)(x + √3)(2x2 - 2x - x + 1)
= (x - √3)(x + √3)(2x(x - 1) - 1(x - 1))
= (x - √3)(x + √3)(2x - 1)(x - 1)
Hence,
2x - 1 = 0 or x - 1 = 0
⇒ x = (1/2) or x = 1
Hence, other two zeroes are 1/2 or 1.
Q.30. Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
Let ΔPQR and ΔABC be two similar triangles,
[Corresponding sides of similar triangles are in the same ratio] [1]
And as corresponding angles of similar triangles are equal
∠A = ∠P
∠B = ∠Q
∠C = ∠R
Construction: Draw PM ⏊ QR and AN ⏊ BC
In ΔPQR and ΔABC
∠PMR = ∠ANC [Both 90°]
∠R = ∠C [Shown above]
ΔPQR ~ ΔABC [By Angle-Angle Similarity][Corresponding sides of similar triangles are in the same ratio] [2]
Now, we know that
Area of a triangle
Therefore,[From 2]
[From 1]
[From 1]
Hence, Proved.
Q.31. In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle. Prove it.
Let us consider a triangle ABC, in which
AC2 = BC2 + AB2 …[1]
To Prove: Angle opposite to the first side i.e. AC is right angle or
∠ ABC = 90°
Construction:
Let us draw another right-angled triangle PQR right-angled at Q, with
AB = PQ
BC = QR
Now, By Pythagoras theorem, In ΔPQR
PR2 = QR2 + PQ2
But QR = BC and PQ = AB
⇒ PR2 = BC2 + AB2
But From [1] we have,
AC2 = PR2
⇒ AC = PR
In ΔABC and ΔPQR
AB = PQ [Assumed]
BC = QR [Assumed]
AC = PR [Proved above]
⇒ ΔABC ≅ ΔPQR [By Side-Side-Side Criterion]
⇒ ∠ABC = ∠PQR [Corresponding parts of congruent triangles are equal]
But, ∠PQR = 90°
⇒ ∠ABC = 90°
Hence, Proved !
Q.32. Prove that 
Taking LHS
Dividing by cosθ in numerator and denominator
Usingand
Putting 1 = sec2θ - tan2θ in numerator
Using a2 - b2 = (a + b)(a - b)
= tan θ + sec θ
Now, taking RHS
Multiplying and dividing by secθ + tanθ = 1
= tanθ + secθ [As sec2θ - tan2θ = 1]
LHS = RHS
Hence Proved.
Q.33. Evaluate: 
Using cosec(90° - θ) = secθ
and cot(90° - θ) = tanθ
we have,
Now, sin(90 - θ) = cos θ and
tan(90 - θ) = cot θ we have
[ Since,
tan2θ - sec2θ = 1
sin2θ + cos2θ = 1
tan 60° = √3]
Q.34. If secθ + tanθ = x, prove that sinθ = 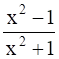
Taking RHS
Now, sec2θ - tan2θ = 1 and (a + b)2 = a2 + b2 + 2ab
Now,and
, using these we have
= LHS
Hence, Proved !
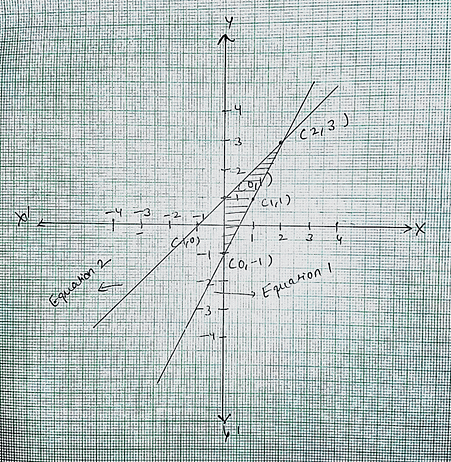
Q.35. Solve the following system of linear equations graphically:
2x - y = 1, x - y = -1.
Shade the region bounded by these lines and the y-axis.
Equation 1:
2x - y = 1
Plot the line with equation 1 on graph.
Equation 2:
x - y = -1
Plot the line with equation 2 on graph.From the graph We observe point of intersection of two lines is (2, 3)Region bound by these lines and y-axis is shaded in the graph.
Q.36. The following table gives the yield per hectare of wheat of 100 farms of a village:
Change the above distribution to 'more than type' distribution and draw its ogive.
Let us draw cumulative frequency with table for the above data
Taking Yield as x-axis and Cumulative frequencies as y-axis, we draw its more than 'ogive'
Q.37. Solve for x and y:
ax + by-a + b = 0, bx-ay-a-b = O.
Eqn1 : ax + by - a + b = 0
⇒ ax + by = a - b
Multiplying both side by b
⇒ abx + b2y = ab - b2 …[1]
Eqn2 : bx - ay - a - b = 0
⇒ bx - ay = a + b
Multiplying both side by a
⇒ abx - a2y = a2 + ab …[2]
Subtracting [2] from [1]
abx - a2y - (abx + b2y) = a2 + ab - (ab - b2)
⇒ abx - a2y - abx - b2y = a2 + ab - ab + b2
⇒ -y(a2 + b2) = a2 + b2
⇒ -y = 1
⇒ y = 1
Putting value of y in eqn1, we get
ax + b(-1) - a + b = 0
⇒ ax - b - a + b = 0
⇒ ax = a
⇒ x = 1
So, x = 1 and y = -1
Q.38. Prove that:  = (cosecθ - cotθ)2.
= (cosecθ - cotθ)2.
Taking LHS
Multiplying and dividing by (1 - cos θ)
As sin2θ + cos2θ = 1
Hence Proved.
Q.39. Δ ABC is right angled at B and D is the midpoint of BC.
Prove that: AC2 = (4AD2 - 3AB2).
Given: A ΔABC right-angled at B, and D is the mid-point of BC, i.e. BD = CD
To Prove: AC2 = (4AD2 - 3AB2)
Proof:
In ΔABD,
By Pythagoras theorem, [i.e. Hypotenuse2 = Base2+ Perpendicular2]
AD2 = AB2 + BD2
[as D is mid-point of BC, therefore,
⇒ 4AD2 = 4AB2 + BC2
⇒ BC2 = 4AD2 - 4AB2 [1]
Now, In ΔABC, again By Pythagoras theorem
AC2 = AB2 + BC2
AC2 = AB2 + 4AD2 - 4AB2 [From 1]
AC2 = 4AD2 - 3AB2
Hence Proved !
Q.40. Find the mean, mode and median of the following data:
Let us make the table for above data and containing cumulative frequency and mid-values for each data
MEAN
We know, that
MODE
In the given data,
The maximum class frequency is 30. So, the modal class is 30-40.
Lower limit(l) of modal class = 30
Class size(h) = 40 - 30 = 10
Frequency(f1) of modal class = 30
Frequency(f0) of class preceding the modal class = 18
Frequency(f2) of class succeeding the modal class = 20
And we know,
Substituting values, we get
MEDIAN
In this case,
Sum of all frequencies, n = 100
Now, we know the median class is whose cumulative frequency is greater than and nearest to.
As, Cumulative frequency greater than and nearest to 50 is 63, the median class is 30 - 40.
Median
where l = lower limit of median class,
n = number of observations,
cf = cumulative frequency of class preceding the median class,
f = frequency of median class,
h = class size
In this case,
l = 30
n = 100
cf = 33
f = 30
h = 10
Putting values, we get,
Median
|
53 docs|15 tests
|
|
53 docs|15 tests
|

|
Explore Courses for Class 10 exam
|

|
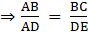 [Corresponding sides of similar triangles are in the same ratio]
[Corresponding sides of similar triangles are in the same ratio]
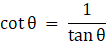
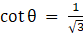 as tanθ = √3
as tanθ = √3
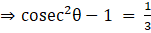 [As cot2θ + 1 = cosec2θ]
[As cot2θ + 1 = cosec2θ]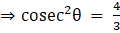 …[2]
…[2]
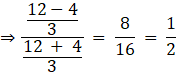

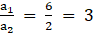 and
and  and
and 
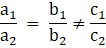

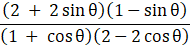

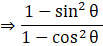


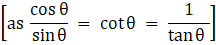

 …[1]
…[1]
 [From [1]]
[From [1]]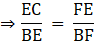

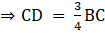 [1]
[1]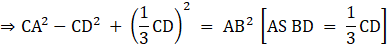
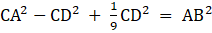

 [From [1]]
[From [1]]
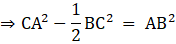





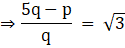
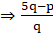 is a rational number.
is a rational number.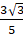 be rational,
be rational,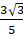 can be expressed as
can be expressed as  where p and q are co-prime integers and
where p and q are co-prime integers and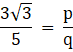

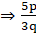 is a rational number.
is a rational number.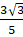 is a rational number.
is a rational number.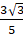 is an irrational number.
is an irrational number.
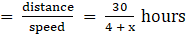
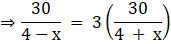
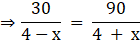
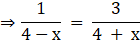
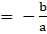
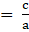
 ….[1] and
….[1] and ….[2]
….[2]


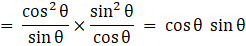
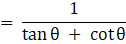


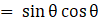


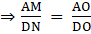 [Corresponding sides of similar triangles are in the same ratio] [1]
[Corresponding sides of similar triangles are in the same ratio] [1]
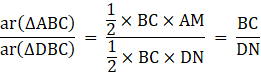
 [From [1]]
[From [1]]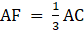


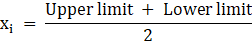

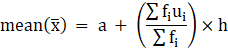
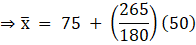
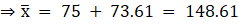


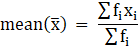
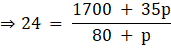

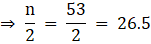
 .
.
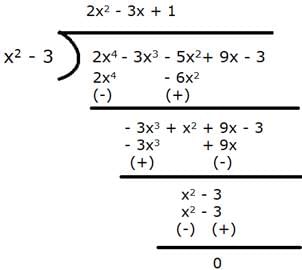
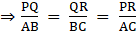
 [Corresponding sides of similar triangles are in the same ratio] [2]
[Corresponding sides of similar triangles are in the same ratio] [2]
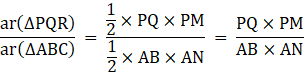
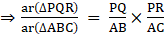 [From 2]
[From 2]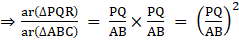 [From 1]
[From 1] [From 1]
[From 1]

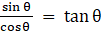 and
and 
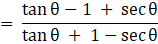
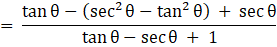



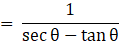
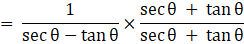
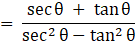

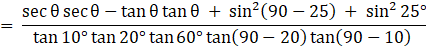

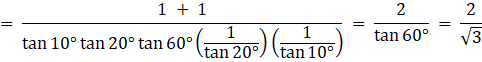

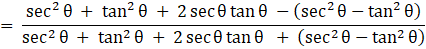
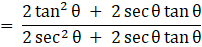

 and
and 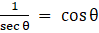 , using these we have
, using these we have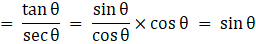




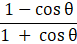
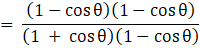





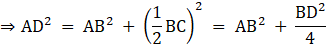



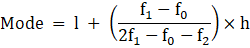
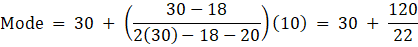

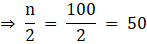
 .
.