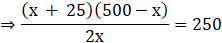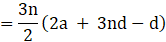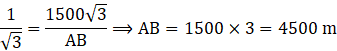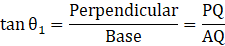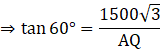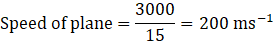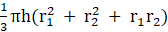RS Aggarwal Solutions: Summative Assessment- 2 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
Sample Paper: II
Q.1. The values of k for which the equation 2x2 + kx + 3 = 0 has two real equal root are
(a) ± 2√ 3
(b) ± 3√ 2
(c) ± 2√ 6
(d) ± √ 6
Any quadratic equation in the form ax2 + bx + c = 0 has equal roots if and only if Discriminant, D = 0
Where, D = b2 – 4ac
In the given equation,
a = 2
b = k
c = 3
Now, above equation will have equal roots if
D = 0
i.e.
(k)2 – 4(2)(3) = 0
⇒ k2 = 24
⇒ k= ±2√6
Q.2. How many terms are there in the AP 7, 11,15, …, 139?
(a) 31
(b) 32
(c) 33
(d) 34
In the given AP,
First term, a = 7
Common difference, a2 – a1 = (11 – 7) = 4
Let the no of terms be n
Nth term, an = 139
We know that, For any AP
an = a + (n – 1)d
where,
an = nth term
d = common difference
n = no of terms using the above formula for given AP, we have
139 = 7 + (n – 1)(4)
⇒ 4(n – 1) = 132
⇒ n – 1 = 33
⇒ n = 34
Hence, there are 34 terms in given AP.
Q.3. One card is drawn from a well-shuffled deck of card. The probability of drawing a 10 of a black suit is
(a) 1/13
(b) 1/26
(c) 1/52
(d) 3/52
We know that,
Probability
Now,
No of total outcomes i.e. total no of cards = 52
No of favourable outcomes i.e. no of black suits of 10 = 2
Probability (Getting a 10 of black suit) = 2/52 = 1/26
Q.4. In a circle of radius 7 cm, tangent PT is drawn from a point P such that PT = 24 cm. If O is the centre of the circle then OP =?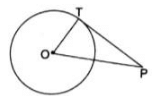
(a) 30 cm
(b) 28 cm
(c) 25 cm
(d) 31 cm
Given, A circle with center O and radius, OT = 7 cm and PT = 24 cm
Now, we know that
Tangent at a point on the circle is perpendicular to the radius through the point of contact.
i.e.
OT ⏊ OP
By Pythagoras Theorem in ΔOTP [ i.e. Hypotenuse2 = Base2 + Height2]
(OP)2 = (OT)2 + (PT)2
⇒ (OP)2 = (7)2 + (24)2
⇒ (OP)2 = 49 + 576 = 625
⇒ OP = 25 cm
Q.5. The ratio in which the line segment joining the points A(– 3/ 2) and B(6, 1) is divided by the y – axis is
(a) 3:1
(b) 1:3
(c) 2:1
(d) 1:2
We know that any point on y axis is in the form (0, x) where x is any real number, let y axis intersect the line segment AB at point P with coordinates (0, c)
And we have
Coordinates of A = (– 3, 2)
Coordinates of B = (6, 1)
Let P divides AB in K:1
Now, By using section formula i.e.
The coordinates of Point P which divides line AB in a ration m : n is
Where, (x1, y1) and (x2, y2) are the coordinates of points A and B respectively.
So,
Coordinates of P
So,
P divides AB in 2:1.
Q.6. The distance of the point P (6, – 6) from the origin is
(a) 6 units
(b) √ 6 units
(c) 3√ 2 units
(d) 6√ 2 units
Coordinates of Given Point (say P) = (6, – 6)
Coordinates of Origin (say O) = (0, 0)
By using distance formula i.e
Distance
Where, (x1, y1) and (x2, y2) are the coordinates of points A and B respectively.
So, we have
⇒ OP =√(36 + 36)
⇒ OP =6√2 units
Q.7. A kite is flowing at a height of 75 cm from the level ground, attached to a string inclined at 60˚ to the horizontal. The length of string with no slack in it, is
(a) 50√ 2 m
(b) 25√ 3 m
(c) 50√ 3 m
(d) 37.5 m
Consider, the situation in the form of a triangle ABC where A is the kite and AC shows the height of kite i.e.
AC = 75 cm
And
AB be the string with angle of inclination i.e.
∠CAB = θ = 60°
We have to find length of string i.e. AB
Clearly, ABC is a right – angled triangle
So, we have
On cross multiplying we get,
On rationalizing we get,
Q.8. A solid metal cone with radius of base 12 cm and height 24 cm is melted to form solid spherical balls of diameter 6 cm each. The number of balls formed is
(a) 16
(b) 32
(c) 24
(d) 28
For solid metal cone,
Height, h = 24 cm
Base radius, b = 12 cm
We know,
Where r is base radius and h is the height of cone.
Putting the values,
For a solid spherical ball,
Diameter = 6 cm
Radius, r = 3 cm
We know,
Where, r is radius of sphere.
Putting the values, we have
On solving, we get
No of balls = 32
Q.9. If the roots of the equation (a – b) x2 + (b – c) + (c – a) = 0 are equal, prove that b + c = 2a.
As the equation is in the form Ax2 + Bx + C = 0 with non-zero A.
In which,
A = a - b
B = b - c
C = c - aAnd we know that if the roots of a equation are equal then we have
Discriminant, D = 0
Where, D = b2 - 4ac
⇒ b2 - 4ac = 0
⇒ (b - c)2 - 4(a - b)(c - a) = 0
⇒ (b - c)2 + 4(a - b)(a - c) = 0
⇒ b2 + c2 - 2bc + 4(a2 - ac - ab + bc) = 0
⇒ b2 + c2 - 2bc + 4a2 - 4ac - 4ab + 4bc = 0
⇒ 4a2+ b2 + c2 - 4ac + 2bc - 4ac = 0
⇒ (-2a)2+ b2 + c2 + 2(-2a)c + 2bc + 2(-2a)c = 0
⇒ (-2a + b + c)2 = 0
[using (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2za ]
⇒ -2a + b + c = 0
⇒ b + c = 2a
Hence Proved.
Q.10. Find the 10th term form the end of the AP 4, 14, … , 254.
First term, a = 4
Common difference, a2 – a1 = 14 – (4) = 10
Let the no of terms be n
We know, that nth term of an AP is
an =a + (n – 1)d
where a is first term and d is common difference.
254 = 4 + (n – 1)10
⇒ 250 = (n – 1)10
⇒ n – 1 = 25
⇒ n = 26
10th term from last will be 17th term from starting
And a10 = a + 16d
= 4 + 16(10)
= 164
Q.11. Or, which term of the AP 3, 15, 27, 34, … will be 132 more than its 54th term?
Which term of the AP 3, 15, 27, 39, … will be 132 more than its 54th term.
Given AP = 3, 15, 27, 39, …
First term, a = 3
Common difference, a2 - a1 = 15 - 3 = 12
And we know
Nth term of an AP, an = a + (n - 1)d
Where a is first term and d is common difference.
Now, let the mth term be 132 more than 54th term
In that case,
am = a54 + 132
⇒ a + (m - 1)d = a + 53d + 132
⇒ (m - 1)12 = 53(12) + 132
⇒ 12m - 12 = 636 + 132
⇒ 12m = 768 + 12
⇒ 12m = 780
⇒ m = 65
Hence, 65th term will be 132 more than its 54th term.
Q.12. Prove that the tangents drawn at the ends of a diameter of a circle are parallel
Let AB be the diameter of a circle with center O.
CD and EF are two tangents at ends A and B respectively.
To Prove : CD || EF
Proof :
OA ⏊ CD and OB ⏊ EF [Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
∠OAD = ∠OBE = 90°
∠OAD + ∠OBE = 90° + 90° = 180°
Considering AB as a transversal
⇒ CD || EF
[Two sides are parallel, if any pair of the interior angles on the same sides of transversal is supplementary]
Q.13. From an external point P tangents PA and PB are drawn to a circle with centre at the point E and PA = 14 cm, find the perimeter of ΔPCD.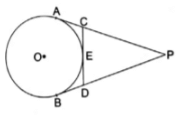
Given: From an external point P, two tangents, PA and PB are drawn to a circle with center O. At a point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. And PA = 14 cm
To Find: Perimeter of ΔPCD
As we know that, Tangents drawn from an external point to a circle are equal.
So we have
AC = CE …[1] [Tangents from point C]
ED = DB …[2] [Tangents from point D]
Now Perimeter of Triangle PCD
= PC + CD + DP
= PC + CE + ED + DP
= PC + AC + DB + DP [From 1 and 2]
= PA + PB
Now,
PA = PB = 14 cm as tangents drawn from an external point to a circle are equal
So we have
Perimeter = PA + PB = 14 + 14 = 28 cm
Q.14. The area of the circular base of a cone is 616 cm2 and its height is 48 cm. Find its whole surface area. [Take π = 22/7.]
Area of circular base = 616 cm2
We know that,
Area of circle = πr2
Where r is the radius of circle
Let the radius of circular base be r
We have,
πr2 = 616 cm2⇒ = 22/7 x r2 = 616
⇒ r2 = 196
⇒ r = 14 cm
Now, Height = 48 cm [Given]
And we know,
Slant height, l =√(r2 + h2)
Where r is radius and h is the height of the cone
l=√(142 + 482)=√(196 + 2304)=√2500=50 cm
Now,
Total surface area of a cone = πr(l + r)
Where r is radius and l is slant height.
So, Putting values we have
Total surface of cone = π(14)(50 + 14)
= 22/7 x 14 x 64 = 2816cm2
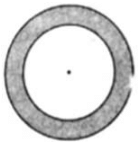
Q.15. In the adjoining figure, the area enclosed between two concentric circles is 770 cm2 and the radius of the outer circle is 21 cm. Find the radius of the inner circle.
Given,
Outer radius of circle, R = 21 cm
Area of enclosed region = 770 cm2
Let the radius of inner circle be r.
Area of enclosed region = Area of outer circle – Area of inner circle
⇒ 770 = πR2 – πr2
⇒ 770/π = R2 - r2
⇒ 770 x 7/22 = R2 - r2
⇒ 35(7) = (21)2 – r2
⇒ r2 = 441 – 245
⇒ r2 = 196
⇒ r = 14 cm.
Q.16. Solve for x: 12abx2 – (9a2 – 8b2) x – 6ab = 0.
12abx2 – (9a2 – 8b2)x – 6ab = 0
12abx2 – 9a2x + 8b2x– 6ab = 0
3ax(4bx – 3a) + 2b(4bx – 3a) = 0
(3ax + 2b)(4bx – 3a) = 0
So, we have
3ax + 2b = 0 or 4bx – 3a = 0
x= -(2b/3a) or x = 3a/4b
Q.17. If the 8th term of an AP is 31 and its 15th term is 16 more than the 11th term. Find the AP.
Let the a be first term and d be common difference
As we know
an = a + (n – 1)d
Given,
⇒ a8 = 31
⇒ a + 7d = 31
⇒ a = 31 – 7d …[1]
Also, As 15th term is 16 more than 11th term
⇒ a15 = a11 + 16
⇒ a + 14d = a + 10d + 16
⇒ 4d = 16
⇒ d = 4
Using this value in equation [1]
a = 31 – 7(4) = 3
So, AP is
a, a + d, a + 2d, …
3, 3 + 4, 3 + 2(4), …
3, 7, 11, …
Q.18. Prove that the parallelogram circumscribing a circle is a rhombus.

Consider a circle circumscribed by a parallelogram ABCD, Let side AB, BC, CD and AD touch circles at P, Q, R and S respectively.
To Proof : ABCD is a rhombus.
As ABCD is a parallelogram
AB = CD and BC = AD [opposite sides of a parallelogram are equal] …[1]
Now, As tangents drawn from an external point are equal.
We have
AP = AS [tangents from point A]
BP = BQ [tangents from point B]
CR = CQ [tangents from point C]
DR = DS [tangents from point D]
Add the above equations
AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ AB + CD = AS + DS + BQ + CQ
⇒ AB + CD = AD + BC
⇒ AB + AB = BC + BC [From 1]
⇒ AB = BC …[2]
From [1] and [2]
AB = BC = CD = AD
And we know,
A parallelogram with all sides equal is a rhombus
So, ABCD is a rhombus.
Hence Proved !
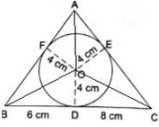
Q.19. A ΔABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of length 8 cm and 6 cm respectively. Find AB and AC.
Given: ΔABC that is drawn to circumscribe a circle with radius r = 4 cm and BD = 6 cm DC = 8 cm
To Find: AB and AC
Now,
As we know tangents drawn from an external point to a circle are equal.
Then,
FB = BD = 6 cm [Tangents from same external point B]
DC = EC = 8 cm [Tangents from same external point C]
AF = EA = x (let) [Tangents from same external point A]
Using the above data we get
AB = AF + FB = x + 6 cm
AC = AE + EC = x + 8 cm
BC = BD + DC = 6 + 8 = 14 cm
Now we have heron's formula for area of triangles if its three sides a, b and c are given
ar = √(s(s – a)(s – b)(s – c))
Where,
So for ΔABC
a = AB = x + 6
b = AC = x + 8
c = BC = 14 cm
And
ar(ΔABC) = √((x + 14)(x + 14 – (x + 6))(x + 14 – (x + 8))(x + 14 – 14))
= √((x + 14)(8)(6)(x)) [1]
ar(ABC) = ar(AOB) + ar(BOC) + ar(AOC)
at, tangent at a point on the circle is perpendicular to the radius through point of contact,
So, we have
OF ⏊ AB, OE ⏊ AC and OD ⏊ BC
Therefore, AOB, BOC and AOC are right – angled triangles.
And area of right angled triangle =1/2 × Base × Height
Using the formula,
Using [1] we have,
Squaring both side
⇒ 48x(x + 14) = (2x + 6 + 28 + 2x + 16)2
⇒ 48x2 + 672x = (56 + 4x)2
⇒ 48x2 + 672x = (4(14 + x))2
⇒ 48x2 + 672x = 16(196 + x2 + 28x)
⇒ 3x2 + 42x = 196 + x2 + 28x
⇒ 2x2 + 14x – 196 = 0
⇒ x2 + 7x – 98= 0
⇒ x2 + 14x – 7x – 98 = 0
⇒ x(x + 14) – 7(x + 14) = 0
⇒ (x – 7)(x + 14) = 0
⇒ x = 7 or x = – 14 cm
Negative value of x is not possible, as length can't be negative
Therefore,
x = 7 cm
⇒ AB = x + 6 = 7 + 6 = 13 cm
⇒ AC = x + 8 = 7 + 8 = 15 cm
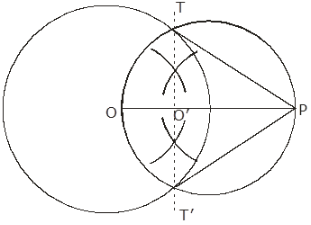
Q.20. Draw a circle of diameter 12 cm. From a point 10 cm away its centre, construct a pair of tangents to the circle. Measure the length of each tangent segment.
Steps of Construction:
1. Take a point O and draw a circle of radius 6 cm [ i.e. diameter 12 cm]
2. Mark a point P at a distance of 10 cm from O in any direction. Join OP
3. Draw right bisector of OP, intersecting OP at O'
4. Taking O' as center and O'O=O'P as radius, draw a circle to intersect the previous circle at T and T'.
5. Join PT and PT', which are required tangents.
6. Measured PT and PT' by a ruler and we get PT = PT' = 8 cm
Q.21. Show that the point A (a, a), B (– a, – a) and C(– a√ 3, a√ 3) are the vertices of an equilateral triangle.
For the points A, B and C to be vertices of an equilateral triangle,
AB = BC = CA and we have distance formula,
For two point P(x1, y1) and Q(x2, y2)
PQ= √((x2 – x1)2 + (y2 – y1)2)
Using the above formula, and coordinates we have
AB=√((– a – a)2 + (– a – a)2)
⇒ AB= √(4a2 + 4a2 )=√8 a
As AB = BC = AC
ABC is an equilateral triangle.
Q.22. Find the area of a rhombus if its vertices are A (3, 0), B (4, 5), C (– 1, 4) and D (– 2, – 1).
As the diagonal of rhombus divides it into two parts, it is sufficient to calculate the area of one part and double it.
Consider, the Diagonal AC,
Then,
ar(ABCD) = 2× ar(ΔABC)
Now,
A = (3,0); B = (4, 5); C = (– 1, 4)
As we know area of triangle formed by three points (x1, y1), (x2, y2) and (x3, y3)
= 6 square units
⇒ ar(ABCD) = 2× ar(ΔABC) = 2(6) = 12 square units
Q.23. Cards marked with numbers 13, 14, 15, …, 60 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that the number on the card drawn is (a) Divisible by 5 (b) a number which is a perfect square
Total no of numbers = 60 – 13 + 1 = 48
[As total no's from a to b are (b – a + 1)]
(a) No Divisible by 5 in the given sequence = {15, 20, 25, 30, 35, 40, 45, 50, 55, 60}
So, we have
No of favourable outcomes = 10
No of total outcomes = 48
And,
Probability of an event
Therefore,
P(Getting a card having no divisible by 5) = 10/48 = 5/24
(b) Perfect squares in the given sequence = {16, 25, 36, 49}
So, we have
No of favourable outcomes = 4
No of total outcomes = 48
And,
Probability of an event
Therefore,
P(Getting a card having a perfect square) = 4/48 = 1/12.
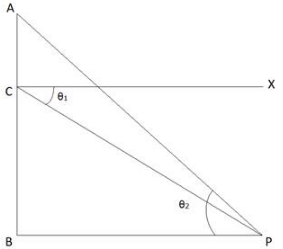
Q.24. A window in a building is at a height of 10 m from the ground. The angle of depression of a point P on the ground from the window is 30˚. The angle of elevation of the top of the building from the point P is 60˚. Find the height of the building.
Let us consider this situation by a diagram as shown, in which AB is a building and C depicts the window and A be the top.
Now Given,
Height of window from the ground, BC = 10 m
Angle of depression of point P from window, ∠XCP = 30°
⇒ ∠XCP = ∠CPB = θ1 = 30° [Alternate Angles]
Angle of elevation of top of the building from point P, ∠APB = 60°
⇒ ∠ APB = θ2 = 60°
Now, In Δ BCP
Cross – Multiplying we get,
BP=10√3 meters
Now, In ΔABP
⇒ AB = 10√3 × √3 = 30 meters
So, Height of building is 30 meters.
Q.25. In a violent storm, a tree got bent by the wind. The top of the tree meet the ground at an angle of 30˚, at a distance of 30 metres from the root. At what height from the bottom did the tree get bent? What was the original height of the tree?
Let AB be a tree, and P be the point of break,
And As tree falls, we can consider the situation as a right angled triangle at B
Given,
Angle of broken tree with ground, θ = 30°
Distance of top of broken tree from root, AB = 30 m
In ΔAPB
So, tree bents at a height of 10√3 meters from the ground.
Also, In Δ APB
On cross – multiplying
AP = 10√3 × 2 = 20√3 meters
Original height of tree = AP + BP
= 20√3 + 10√3
= 30√3 meters
Q.26. A wire bent in the form of a circle of radius 42 cm is cut and again bent in the form of a square. Find the ratio of the areas of the regions enclosed by the circle and the square.
Given,
Radius of circle made by wire, r = 42 cm
Circumference of circle of radius r = 2πr
Circumference of circle made by wire = 2 x (22/7) x 42 = 264 cm2
As, the same wire is bent to make a square the perimeter of square will be equal to circumference of circle.
Let the side of square be a.
Perimeter of square of side 'a' = 4a
We have,
4a = 264
a = 66 cm
Now,
Ratio of areas
Area of circle of radius r = πr2
Area of square of radius a = a2
Putting value, we get
Ratio of areas
Required ratio is 14 : 11
Q.27. A metallic sphere of radius 10.5 cm is melted and then recast into smaller cones, each of radius 3.5 cm and height 3 cm. How many cones are obtained?
We know volume of sphere of radius R is 4/3πR3
And
Volume of cone of radius r and height h is 1/3πr2h
So, Given,
Radius of sphere, R = 10.5 cm
Radius of cone, r = 3.5 cm
Height of cone, h = 3 cm
No of cones can be made by melting sphere
Using formulas, and putting values
No of cones
Hence, 126 cones can be made.
Q.28. In the given figure ΔABC is right angled at A. Semicircles are drawn on AB, AC and BC as diameter. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.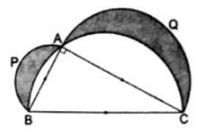
Let semicircle I, II and III are semicircles with diameters AB, AC and BC respectively
Area of shaded region =
Area of semicircle I + Area of semicircle II + Area of triangle ABC – Area of semicircle III
As, ∠BAC is in semicircle,
∠BAC = 90° [Angle in a semicircle is right angle]
And ABC is a right – angled triangle at A
By Pythagoras Theorem
(Hypotenuse)2 = (Base)2 + (Perpendicular)2
(BC)2 = (AB)2 + (AC)2
⇒ (BC)2 = 32 + 42 = 9 + 16 = 25
⇒ BC = 5 cm
Now, For semicircle I
Diameter = AB = 3 cm
Radius
Area of semicircle of radius r
Area of semicircle I
For semicircle II
Diameter = AC = 4 cm
Radius
Area of semicircle of radius r = πr2/2
Area of semicircle II
For semicircle III
Diameter = BC = 5 cm
Radius,
Area of semicircle of radius r = πr2/2
Area of semicircle I
Area of a right – angled triangle
Area of ΔABC
Required area (From eqn [1])
Q.29. ₹ 250 is divided equally among a certain number of children. If there were 25 more children, each would have received 50paise less. Find the number of children.
Let the no of children is x and amount given to each child is y
As the total amount is 250 ₹
We have,
xy = 250
⇒ y = 250/x ...[1]
Also, given if no of children is increased by 25, the amount to each get less by 50 paise i.e. 0.5 ₹
So, we have
(x + 25)(y – 0.5) = 250[By 1]
⇒ 500x – x2 + 12500 – 25x = 500x
⇒ x2 + 25x – 12500 = 0
⇒ x2 + 125x – 100x – 12500 = 0
⇒ x(x + 125) – 100(x + 125) = 0
⇒ (x – 100)(x + 125) = 0
so,
⇒ x – 100 = 0 or x + 125 = 0
⇒ x = 100 or – 125
However, no. of students can't be negative
Hence, x = 100
So, there were 100 students.
Q.30. The hypotenuse of a right – angled triangle is 6 cm more than twice the shortest side. If the third side 2 cm less than the hypotenuse, find the sides of the triangle.
Let the shortest side be x cm [Let it be base]
Length of hypotenuse = 2x + 6 [in cm]
Length of other side = Length of hypotenuse – 2 = 2x + 6 – 2 = 2x + 4 [in cm] [Let it be perpendicular]
As we know, By Pythagoras Theorem
(hypotenuse)2 = (base)2 + (perpendicular)2
⇒ (2x + 6)2 = x2 + (2x + 4)2
⇒ 4x2 + 36 + 24x = x2 + 4x2 + 16 + 16x
[(a + b)2 = a2 + b2 + 2ab]
⇒ x2 – 8x – 20 = 0
⇒ x2 – 10x + 2x – 20 = 0
⇒ x(x – 10) + 2(x – 10) = 0
⇒ (x + 2)(x – 10) = 0
⇒ x = – 2 or x = 10 cm
However, Length can't be negative hence x = – 2 is not possible
Therefore,
x = 10 cm
we have,
Shortest Side = x = 10 cm
Hypotenuse = 2x + 6 = 2(10) + 6 = 26 cm
Third side = 2x + 4 = 2(10) + 4 = 24 cm
Q.31. If the sum of first n, 2n and 3n term of an AP be S1 , S2 and S3 respectively, then prove that S3 = 3 (S2 – S1).
We know that sum of first n terms of an AP is
Sn = n/2(2a + (n-1)d)
Where a is first term and d is common difference
So,
Sum of first 2n terms
Sum of first 3n terms
Now, Taking RHS
RHS = LHS
Hence Proved.
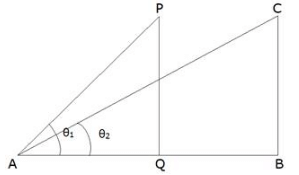
Q.32. The angle of elevation of a jet plane from point A on the ground is 60˚. After A flight of 15 seconds, the angle of elevation changes to 30˚. If the jet plane is flying at a constant height of 1500 √ 3 m, find the speed of the jet plane.
Let the jet plane goes from point P to point C and we have given,
Initially angle of elevation from point A, ∠PAQ = θ1 = 60°
After 15 seconds,
Angle of elevation from point A, ∠CAB = θ2 = 30°
As the plane is flying at a constant height,
BC = PQ = 1500√3 m
Now,
In ΔABC
In ΔAPQ
So, we have
QB = AB – AQ = 4500 – 1500 = 3000 m
And
QB = PC
So, jet plane travels 3000 m in 15 seconds
And we know,
Q.33. Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Given: A circle with center O and P be any point on a circle and XY is a tangent on circle passing through point P.
To prove : OP⏊XY
Proof :
Take a point Q on XY other than P and join OQ .
The point Q must lie outside the circle. (because if Q lies inside the circle, XY will become a secant and not a tangent to the circle).
Therefore, OQ is longer than the radius OP of the circle. That is, OQ > OP.
Since this happens for every point on the line XY except the point P, OP is the shortest of all the distances of the point O to the points of XY.
So OP is perpendicular to XY.
[As Out of all the line segments, drawn from a point to points of a line not passing through the point, the smallest is the perpendicular to the line.]
Q.34. A quadrilateral ABCD is drawn to circumscribe a circle, as shown in the given figure. Prove that: AB + CD = AD + BC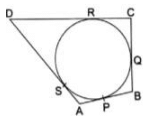
Given: A quadrilateral ABCD, And a circle is circumscribed by ABCD
Also, Sides AB, BC, CD and DA touch circle at P, Q, R and S respectively.
To Prove: AB + CD = AD + BC
Proof:
In the Figure,
As tangents drawn from an external point are equal.
We have
AP = AS [tangents from point A]
BP = BQ [tangents from point B]
CR = CQ [tangents from point C]
DR = DS [tangents from point D]
Add the above equations
⇒ AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ AB + CD = AS + DS + BQ + CQ
⇒ AB + CD = AD + BC
Hence Proved.
Q.35. A solid is made up of a cube and a hemisphere attached on its top as shown in the figure. Each edge of the cube measures 5 cm and the hemisphere has a diameter of 4.2 cm. Find the total area to be painted.
Total area to be painted = TSA of cube + CSA of hemisphere – Base area of hemisphere
[TSA = Total surface area & CSA = Curved surface area]
Given,
Diameter of hemisphere = 4.2 cm
Radius of hemisphere, r = 2.1 cm [Radius = [Diameter/2]]
Side of cube, a = 5 cm
And
TSA of cube = 6a2, where a is the side of cube
CSA of hemisphere = 3πr2, where r is the base radius
Base area = πr2 [As base is circular]
Therefore,
Total area to be painted = 6a2 + 3πr2 – πr2 = 6a2+ 2πr2
= 6(25) + (2 × 22 × 0.3 × 2.1)
= 177.72 cm2
Q.36. The diameter of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm. find:
(i) The capacity of the bucket
(ii) The area of the metal sheet used to make the bucket. [Take π = 3.14.]
Given,
The diameter of lower end = 10 cm
As Radius = Diameter/2
Radius of lower end, r2 = 5 cm
The diameter of upper end = 30 cm
Radius of upper end, r1 = 15 cm
Height of bucket, h = 24 cm
(i) As we know
volume of frustum of a cone =
Where, h = height, r1 and r2 are radii of two ends (r1 > r2)
Capacity of bucket
=3.14 × 8 × (25 + 225 + 75)
= 3.14 × 8 × 325 = 8164 cm3
(ii) Area of metal used to make bucket = CSA of frustum + base area
We know that,
Curved surface area of frustum = πl(r1 + r2)
Where, r1 and r2 are the radii of two ends (r1 > r2)
And l = slant height and
l = √(h2+ (r1 – r2 )2)
So, we have
Slant height, l=√(242 + (15 – 5)2)
⇒ l =√(576 + 100)
⇒ l =√676
⇒ l = 26 cm
And as the base has lower end,
Base area = πr22, where r2 is the radius of lower end
Therefore,
Area of metal sheet used = πl(r1 + r2) + πr22
= π(26)[15 + 5] + π(5)2
= 520π + 25π
= 545π
= 545(3.14)
=1711.3 cm2
Q.37. Find the value of k for which the point A (– 1, 3), B (2, k) and C (5, – 1) are collinear.
Three points A, B and C are collinear if and only if
Area(ΔABC) = 0
As we know area of triangle formed by three points (x1, y1), (x2,y2) and (x3, y3)
⇒ 0= – 6k + 6
⇒ 6k = 6
⇒ k = 1
So, For k = 1, A, B and C are collinear.
Q.38. Two dice are thrown at the same time. Find the probability that the sum of two numbers appearing on the top of the dice is more than 9.
When two dice are thrown, the possible outcomes are
{(1,1) (1,2) (1,3) (1,4) (1,5) (1,6), (2,1) (2,2) (2,3) (2,4) (2,5) (2,6), (3,1) (3,2) (3,3) (3,4) (3,5) (3,6), (4,1) (4,2) (4,3) (4,4) (4,5) (4,6), (5,1) (5,2) (5,3) (5,4) (5,5) (5,6), (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)}
The outcomes in which sum of no's is 9 are ={(3,6) (4,5) (5,4) (6,3)}
No of Total possible outcomes = 36
No of favourable outcomes = 4
And, Probability of an event
Therefore,
P(Getting sum 9) = 4/36 = 1/9
Q.39. A circus tent is cylindrical to a height of 3 cm and conical above it. If its base radius is 52.5 m and the slant height of the conical portion is 53 m, find the area of canvas needed to make the tent. [Take π = 22/7.]
Total area of canvas required = CSA of cylindrical part + CSA of conical part [CSA = Curved surface area]
Now,
Radius of cone = Radius of cylinder = r = 52.5 m
Height of cylindrical part, h = 3 cm = 0.03 m [As 1 m = 100 cm]
Lateral height of conical part, l = 53 m
Now, we know
CSA of cylinder = 2πrh
Where, r is base radius and h is height of cylinder and
CSA of cone = πrl
Where, r is base radius and l is slant height.
Area of canvas required = 2πrh + πrl
= πr(2h + l)
= 8754.9 m2
|
53 docs|15 tests
|
|
53 docs|15 tests
|

|
Explore Courses for Class 10 exam
|

|
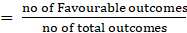





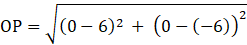

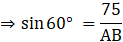

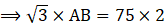
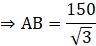

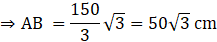
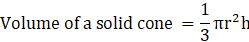
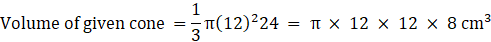

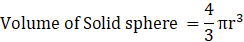
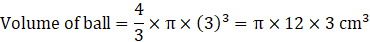
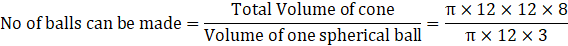


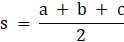
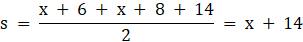


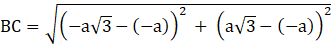


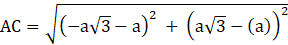



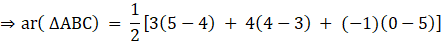
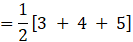






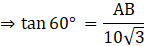
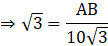

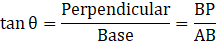
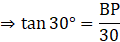
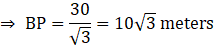



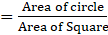

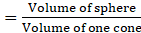


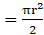




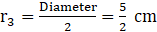
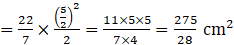


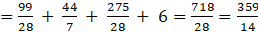
 [By 1]
[By 1]