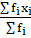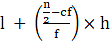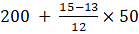RS Aggarwal Solutions: Summative Assessment- 2 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
Sample Paper: II
Q.1. What is the largest number that divides 245 and 1029, leaving remainder 5 in each case?
(a) 15
(b)16
(c) 9
(d) 5
We know that Dividend = Divisor × Quotient + Remainder
According to the problem :
Dividend 1 = 245
Dividend 2 = 1029
Dividend - Remainder = Divisor × Quotient
So Dividend 1- Remainder = 240 = Divisor × Quotient 1
Prime Factor of 240 = 24 × 3 × 5
Dividend 2 – Remainder = 1024 = Divisor × Quotient 2
Prime Factor of 1024 = 24 × 26
Since, the Divisor is common for both the numbers we need to find the Highest Common Factor between both the numbers. From the Prime factors, we find the
Highest Common Factor between the two numbers is 24 = 16
Q.2. If the product of zeros of the polynomial ax2 – 6x – 6 is 4, then a =?
(a) 2/3
(b) –2/3
(c) 3/2
(d) –3/2
Given Equation :ax2 – 6x – 6 = 0
which is of the form ax2 + bx + c = 0 (General Form)
The product of the roots of the general form of equation = c/a
So according to the given Equation Product of the roots = -(6/a)
⇒ - (6/a) = 4
The Value Of a for which the equation has product of root 4 = a = -(3/2)
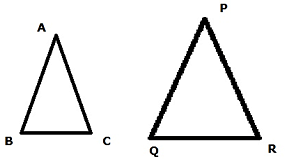
Q.3. The areas of two similar triangles ΔABC and ΔPQR are 25 cm2 and 49 cm2 respectively and QR = 9.8 cm. Then BC = ?
(a) 5 cm
(b) 8 cm
(c) 7 cm
(d) 6.3 cm
Given :
Area of ΔABC = 25 cm2
Area of ΔPQR = 49 cm2
Length of QR = 9.8 cm.
Since both the triangles are similar so according to the Area –Length relations of similar triangle we can write
The length Of The side BC is 7 cm.
Q.4. If sin (θ + 34°) = cos θ and θ + 34° is acute, then θ = ?
(a) 56°
(b) 28°
(c) 17°
(d) 14°
Given sin (θ + 34°) = cos θ …Equation 1
Since sin θ & cos θ are complementary to each other
so sin θ = cos (90° – θ)
Using the above relations in Equation 1 we get
cos (90° – θ – 34°) = cos θ
Since both L.H.S. and R.H.S. are functions of cosine and θ + 34° is acute so we can write
90° – θ – 34° = θ
⇒ 2θ = 56°
⇒ θ = 28°
Q.5. lf cos θ = 0.6, then 5sin θ - 3tan θ = ?
(a) 0.4
(b) 0.2
(c) 0.3
(d) 0
Given cos θ = 0.6
⇒ sin θ = 0.8
According to the question, the required problem needs us to find
5 sin θ- 3 tan θ
The value of the expression is 0.
Q.6. The simplest form of 1095/1168
(a) 17/26
(b) 25/26
(c) 15/16
(d) 13/16
Prime factorization of 1095 = 5×3×73
Prime factorization of 1168 = 24 ×73
So
Since 73 is a common factor for both numerator and denominator so it cancels out
The Simplest form is 15/16.
Q.7. The pair of linear equations 4x - 5y - 20 = 0 and 3x + 5y -15 = 0 has
(a) a unique solution
(b) two solutions
(c) many solutions
(d) no solution
Equation 1: 4x - 5y = 20
Equation 2: 3x + 5y = 15
Both the equations are in the form of :
a1x + b1y= c1 & a2x + b2y = c2 where
According to the problem:
a1 = 4
a2 = 3
b1 = -5
b2 = 5
c1 = 20
c2 = 15
We compare the ratios
Since, So
It has a Unique solution
Q.8. If mode = x(median) - y(mean), then
(a) x = 2, y = 3
(b) x = 3, y = 2
(c) x = 4, y = 3
(d) x = 3, y = 4
Given: mode = x(median) - y(mean)
According to an empirical relation, the relation between Mean, Median & Mode is given by
Mode = 3 Median – 2 Mean …Eq(1)
This empirical relation is very much close to the actual value of mode which is calculated. So this relation is valid.
Comparing the Relation given with equation 1 we find
x = 3 & y = 2
Q.9. Check whether 6" can end with the digit 0? Justify your answer.
When a number ends with 0 it has to be divisible by the factors of 10 which are 5 and 2
Now 6n = (3 × 2)n …Equation 1
From Equation 1 We can see the factors of 6 are only 3 & 2.
There are no factors as powers of 5 in the factorization of 6
Hence 6n cannot end with 0.
Q.10. Find the zeros of the polynomial 9x2 - 5 and verify the relation between zeros and coefficients.
Given Equation : 9x2 - 5 = 0
which is of the form ax2 + bx + c = 0 (General Form)
For finding the zeroes of the polynomial we use the method of Factorization
9x2 - 5 = 0
⇒ 9x2 = 5
⇒ x2 =
⇒ x =
The zeroes of the polynomial expression are
Q.11. If 2 sin 2θ = √3 find the value of θ.
Given 2 sin 2θ = √3
⇒ sin 2θ = sin 60°
⇒ 2θ = 60°
⇒ θ = 30°
Q.12. If 7 sin2θ + 3 cos2θ = 4, show that tan θ = 1/√3
Given: 7 sin2 θ + 3 cos2 θ = 4
Since sin2 θ + cos2 θ = 1 …Equation 1
So the equation becomes
4 sin2 θ = 1
⇒ sin2 θ = 1/4
From Equation 1 we get
cos2 θ = 3/4
Since
⇒
Hence Proved.
Q.13. In ΔABC, D and E are points on AB and AC respectively such that AD = 5 cm, DB = 8 cm and DE || BC. If AC = 6.5 cm, then find AE.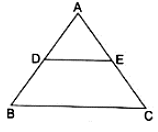
Given :
AD = 5 cm
DB = 8 cm
AC = 6.5 cm
DE ||BC
In ΔABC & ΔADE
∠ADE = ∠ABC (Corresponding Angles)
∠AED = ∠ACB (Corresponding Angles)
So ΔABC & ΔADE are similar by the A.A. (Angle-Angle) axiom of Similarity
AB = AD + BD = 13 cm.
Since the two triangles are similar so their lengths of sides must be in proportion.
⇒
⇒
AE = 2.5cm.
Q.14. D is a point on the side BC of ΔABC such that ∠ADC and ∠BAC are equal. Prove that: CA2 = DC x CB.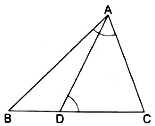
Given:
∠ADC = ∠BAC
D is a point on the side BC
∠ACB = ∠ACD (Common Angle)
So ΔABC & ΔADC are similar by the A.A. (Angle-Angle) axiom of Similarity
Since the two triangles are similar so their lengths of sides must be in proportion
Cross Multiplying We Get
CA2 = DC x CB
Which is the required expression
Hence Proved.
Q.15. Calculate the mode for the following frequency distribution:
Class corresponding to maximum frequency = (4-8)
f1 (Frequency of the modal class) = 8
f0 (Frequency of the class preceding the modal class) = 4
f2 (Frequency of the succeeding modal class) = 5
l(lower limit) = 4
h(width of class) = 4
Mode =
⇒ Mode =
Mode = 6.29.
Q.16. Show that any positive odd integer is of the form (6q + 1) or (6q + 3) or (6q + 5), where q is some integer.
According to Euclid’s algorithm p = 6q + r
where r is any whole number 0< = r<6 and p is a positive integer
Since 6q is divisible by 2 so the value of r will decide whether it is odd or even.
Also since r<6 so only 6 cases are possible
For r = 1 , 3, 5 we get three odd numbers and for r = 0 , 2 , 4 we get three even numbers
So (6q + 1) , (6q + 3) & (6q + 5) represents positive odd integers .
Hence Proved.
Q.17. Prove that (3 -√15) is irrational.
Let us assume (3 -√15 ) is rational
(Assume)
where a & b are integers (b≠0)
⇒
⇒
Now let’s solve the R.H.S. Of the above equation
Let
Squaring we get
In The above equation since 15 divides p2 so it must also divide p
so p is a multiple of 15
let p = 15k where k is an integer
Putting in Equation 1 the value of p we get
15q2 = 225k2
⇒ q2 = 15k2
Since 15 divides q2 so it must also divide q
so q is a multiple of 15
But this contradicts our previously assumed data since we had considered p & q has been resolved in their simplest form and they shouldn't have any common factors.
So √15 is irrational and hence
(3 -√15) is also irrational
Hence Proved.
Q.18. Prove that (2√2)/3 is irrational.
Let us consider
to be rational
where a & b are integers (b≠0)
Rearranging we get
√2 = 3a/2b
The R.H.S of the above expression is a rational number since it can be expressed as a numerator by a denominator
Let L.H.S = P/q where p and q are integers (q≠0)
⇒ √2 = P/q
⇒ q√2 = p
Squaring both sides we get
2q2 = p2…Equation 1
Since 2 divides p2 so it must also divide p
so p is a multiple of 2
let p = 2k where k is an integer
Putting in Equation 1 the value of p we get
2q2 = 4k2
⇒ q2 = 2k2
Since 2 divides q2 so it must also divide q
so q is a multiple of 2
But this contradicts our previously assumed data since we had considered p & q has been resolved in their simplest form and they shouldn't have any common factors.
So √2 is irrational and hence
(2√2)/3 is also irrational
Hence Proved.
Q.19. What number must be added to each of the numbers 5, 9, 17, 27 to make the new numbers in proportion?
Let the number added to each of the numbers to make them in proportion be x
When any four numbers (a, b, c, d)are in proportion then a/b = c/d
Applying the above equation for our problem we get
⇒ (5 + x)(27 + x) = (17 + x)(9 + x)
⇒ 135 + 32x + x2 = 153 + 26x + x2
⇒ 6x = 18
The number added should be 3.
Q.20. The sum of two numbers is 18 and the sum of their reciprocals is 1/4. Find the numbers.
Let the two numbers be x & Y
x + y = 18 (Given) …Equation 1(Given) …Equation 2
Solving Equation 2 We get
Putting the value from Equation 1 we get
⇒ xy = 72
⇒ y = 72/x…Equation 3
Putting the value of Equation 3 in Equation 1 We get
⇒ x + (72/x) = 18
⇒ x2 + 72 = 18x
⇒ x2 - 18x + 72 = 0
⇒ (x-6)2 = 0
⇒ x = 6
Putting the value of x in Equation 1 we get y = 12
The two numbers are 6 & 12.
Q.21. If α, β are the zeros of the polynomial (x2 - x - 12), then form a quadratic equation whose zeros are 2α and 2β.
Given Equation : x2 - x - 12 = 0
which is of the form ax2 + bx + c = 0 (General Form)
The product of the roots of the general form of equation = c/a
Sum of Roots of the general equation = -(b/a)
So α + β = - (b/a)
⇒ α + β = 1
⇒ 2(α + β) = 2 ….Equation 1
Similarly
α×β = -12
⇒ 2α×2β = -48 …Equation 2
The new equation will be formed by combining the results of Equation 1 & 2
The New Polynomial Formed from the new roots is x2 -2x-48.
Q.22. Prove that (sin θ + cosec θ)2 + (cos θ + sec θ)2 = 7 + tan2θ + cot2θ.
Given L.H.S. = (sin θ + cosec θ)2 + (cos θ + sec θ)2
We know
⇒ sin2 θ + cosec2 θ + 2 + cos2 θ + sec2 θ + 2
Also From the Trigonometrical identities
sin2θ + cos2θ = 1
cosec2 θ = 1 + cot2 θ
sec2 θ = 1 + tan2 θ
⇒ 1 + 1 + cot2 θ + 2 + 1 + tan2 θ + 2
⇒ 7 + cot2 θ + tan2 θ
So, L.H.S = R.H.S
Hence Proved.
Q.23. If sec θ + tan θ = m, show that 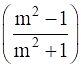 = sin θ.
= sin θ.
Given sec θ + tan θ = m
So, we can write
Squaring both sides we get
Since cos2 θ = 1- sin2 θ
⇒
⇒
Applying Componendo & Dividendo i.e.
is equivalent to
we get
Hence Proved.
Q.24. In a trapezium ABCD, O is the point of intersection of AC and BD, AB|| CD and AB = 2 x CD. If area of ΔAOB = 84 cm2, find the area of ΔCOD.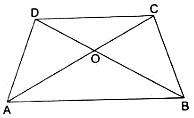
Given :
AB|| CD
AB = 2 x CD
⇒ AB/CD = 2
∠AOB = ∠COD (Vertically Opposite angles)
∠DCO = ∠OAB (Alternate Angles)
So ΔAOB & ΔDOC are similar by the A.A. (Angle Angle) axiom of Similarity
Since both the triangles are similar so according to the Area –Length relations of similar triangle we can write
⇒
Area of ∆DOC = 21cm2.
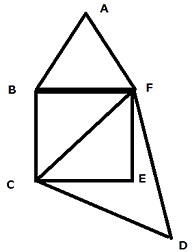
Q.25. In the given figure, AB ⊥ BC, GF ⊥ BC and DE ⊥ AC. Prove that ΔADE ~ Δ GCF.
Given:
AB ⊥ BC
GF ⊥ BC
DE ⊥ AC
Since AB ⊥ BC so ∠DAE & ∠GCF are complementary angles i.e.
∠DAE + ∠GCF = 90° ….Equation 1
Similarly since GF ⊥ BC so ∠CFG & ∠GCF are complementary angles i.e.
∠CGF + ∠GCF = 90° ….Equation 2
Combining Equation 1 & 2 We can say that
∠CGF = ∠DAE
Also ∠CFG = ∠DEA (Perpendicular Angles)
So ΔCGF is similar to ΔADE By A.A. (Angle Angle)axiom of similarity
Hence Proved.
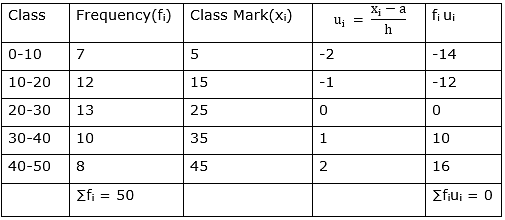
Q.26. Find the mean of the following frequency distribution, using step deviation method:
h (Represents the class width) = 10
a (Assumed mean) = 25
So Mean according to Step Deviation method:
Mean =
Mean = 25
Q.27. The mean of the following frequency distribution is 78. Find the value of p.
Mean = 78 (Given)
According to the direct method
Mean =
⇒ 2886 + 78p = 2665 + 95p
⇒ 17p = 221
Value of p is 13.
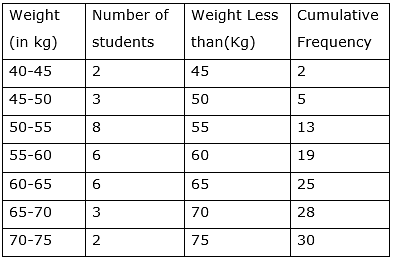
Q.28. Find the median of the following data:
Total frequency(n) = 30
n/2 = 15
15 lies in the interval 55-60
so l (lower limit) = 55
cf(Cumulative frequency of the preceding class of median class) = 13
f (frequency of median class) = 6
h (class size) = 5
Median =
Median =
Median = 56.67Kg.
Q.29. If two zeroes of the polynomial p(x) = 2x4 + 7x3 - 19x2- 14x + 30 are √2 and - √2 then find the other two zeroes.
Given: p(x) = 2x4 + 7x3 - 19x2- 14x + 30
Since x = √2 & - √2 is a solution so
x- √2 & x + √2 are two factors of p(x)
Multiplying the two factors we get x2-2 …Equation 1
which is also a factor of p(x)
To get the other two factors we need to perform long division
On performing long division we will get
2x2 + 7x -15 …Equation 2
Equation 2 is also a factor of p(x)
To find the other two zeroes of the polynomial we need to solve Equation 2
We use the method of factorization for solving Equation 2
2x2 + 7x -15 = 0
⇒ 2x2 + 10x -3x -15 = 0
⇒ 2x(x + 5) -3(x + 5) = 0
⇒ (2x-3)(x + 5) = 0
The two roots are 3/2 and -5.
Q.30. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of an equilateral triangle described on one of its diagonals.
Let us assume BFEC is a square , ΔABF is an equilateral triangle described on the side of the square & Δ CFD is an equilateral triangle describes on diagonal of the square
Now since ΔABF & Δ CFD are equilateral so they are similar
Let side CE = a,
So EF = a
CF2 = a2 + a2
CF2 = 2a2
Since both the triangles are similar so according to the Area –Length relations of similar triangle we can write
⇒
So Area Of Δ CFD = 2 ΔABF
Hence Proved.
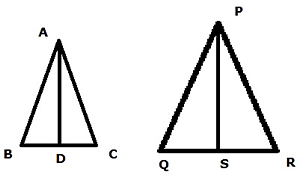
Q.31. Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
Let us assume ΔABC & ΔPQR are similar
Area of ΔABC = 0.5 ×AD ×BC
Area of ΔPQR = 0.5 ×PS ×QR
Now since the two triangles are similar so the length of sides and perpendiculars will also be in proportion…Equation 1
…Equation 2
From Equation 1 We get
Putting in Equation 2 we get
⇒
So we can see ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides
Hence Proved.
Q.32. Prove that: 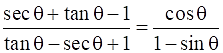
Given: L.H.S. =
Since we know
So L.H.S.
==
Multiplying Numerator & Denominator with sin θ - (1 - cos θ) we get
L.H.S.
=
=
Since sin2 θ + cos2 θ = 1
=
Taking 2 common out of numerator and denominator
=
=
=
=
L.H.S. = R.H.S.
Hence Proved.
Q.33. Evaluate: 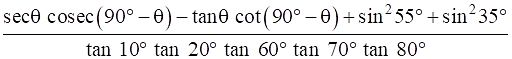
Given:
…Equation 1
We know
sec θ = cosec (900 – θ)
tan θ = cot (900 – θ)
sin θ = cos (900 – θ)
Using the above three relations in Equation 1 we get
We also know
sin2 θ + cos2 θ = 1
⇒ sin2 55 + cos2 55 = 1
And,
∴
⇒
⇒
⇒ 2/√3
2/√3
Q.34. If sec θ + tan θ = m, prove that 
Given sec θ + tan θ = m
So we can write
Squaring both sides we get
Since cos2 θ = 1- sin2 θ
⇒
⇒
Applying Componendo & Dividendo i.e.
is equivalent to
we get
Hence Proved.
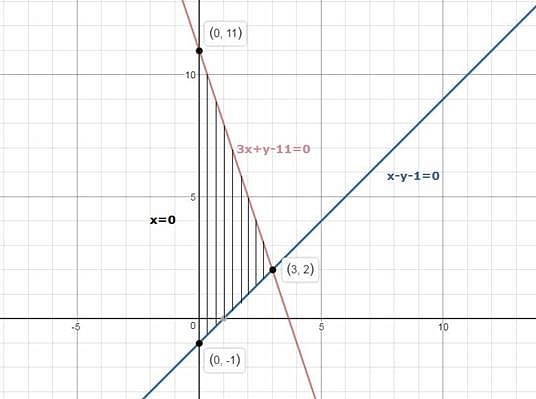
Q.35. Draw the graph of the following equations: 3x + y- 11 = 0 and x-y- 1 = 0.
Shade the region bounded by these lines and the y-axis.
Given: The equations 3x + y- 11 = 0 and x-y- 1 = 0.
To find: the region bounded by these lines and the y-axis.
For 3x + y - 11 = 0
y = 11 - 3x
Now for x = 0
y = 11 - 3(0)
y = 11
For x = 3
y = 11 - 3(3)
y = 11 - 9
y = 2
Table for equation 3x + y -11 = 0 is
Plot the points (0,11),(3,2)
For x-y- 1 = 0
y = x - 1
Now for x = 0
y = 0 - 1
y = -1
For x = 3
y = 3 - 1
y = 2
Table for equation x-y- 1 = 0 is
Plot the points (0,-1),(3,2)
The graph is shown below:
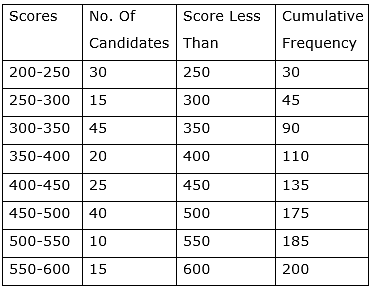
Q.36. The table given below shows the frequency distribution of the scores obtained by 200 candidates in a BCA entrance examination:
Draw cumulative frequency curve using 'less than series'.
Q.37. For what value of k will the following pair of linear equations have infinitely many solutions?
2x - 3y = 7
(k + 1)x + (1 - 2k)y = (5k - 4)
Given:
Equation 1: 2x - 3y = 7
Equation 2: (k + 1)x + (1 - 2k)y = (5k - 4)
Both the equations are in the form of :
a1x + b1y = c1 & a2x + b2y = c2 where
For the system of linear equations to have infinitely many solutions, we must have………(i)
According to the problem:
a1 = 2
a2 = k + 1
b1 = -3
b2 = 1-2k
c1 = 7
c2 = 5k-4
Putting the above values in equation (i) we get:
⇒ 2(1-2k) = -3(k + 1)
⇒ 2-4k = -3k-3
⇒ k = 5
The value of k for which the system of equations has infinitely many solutions is k = 5
Q.38. Prove that: (sin θ – cosec θ)(cos θ – sec θ) = 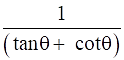
To Prove: (sin
- cosec
)(cos
- sec
) =
L.H.S. = (sin θ –cosec θ)(cos θ- sec θ)
⇒
⇒
Since sin2θ + cos2θ = 1 , So
⇒
After Cancellation we get
L.H.S. = sin θ cos θ
Dividing the numerator and denominator with cos θ we get
⇒
We know
⇒
Since sec2θ = 1 + tan2θ
⇒
Dividing The Numerator and denominator by tan θ we get
⇒
Since= R.H.S
Since L.H.S. = R.H.S
Hence Proved.
Q.39. ΔABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ΔABC is a right triangle.
Given:
AC = BC
AB2 = 2AC2 …(Equation 1)
Equation 1 can be rewritten as
AB2 = AC2 + AC2
Since AC = BC we can write
AB2 = AC2 + BC2 …Equation 2
Equation 2 represents the Pythagoras theorem which states that
Hypotenuse2 = Base2 + Perpendicular2
Since Pythagoras theorem is valid only for right-angled triangle so
SoABC is a right angled triangle right angled at C
Hence Proved.
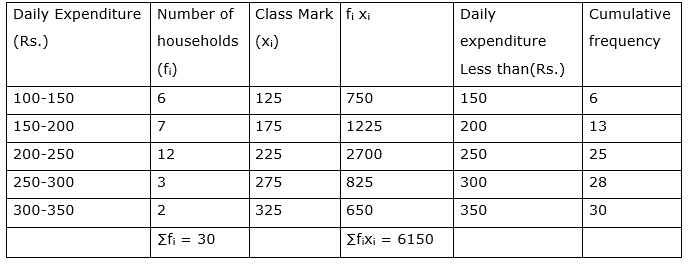
Q.40. The table given below shows the daily expenditure on food of 30 households in a locality: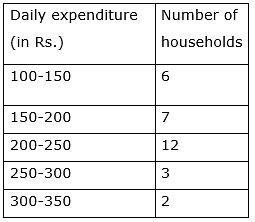
Find the mean and median of daily expenditure on food.
According to the direct method
Mean =
⇒ Mean = 6150/30
⇒ Mean = 205
Total frequency(n) = 30
n/2 = 15
15 lies in the interval 200-250
so l (lower limit) = 200
cf(Cumulative frequency of the preceding class 200-250) = 13
f (frequency of median class) = 12
h (class size) = 50
Median =
Median =
Median = 208.33
|
53 docs|15 tests
|
|
53 docs|15 tests
|

|
Explore Courses for Class 10 exam
|

|
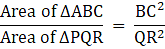
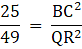
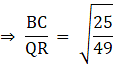
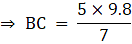
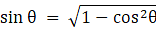
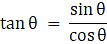
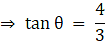
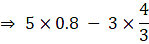

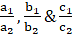
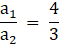
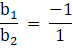
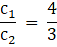
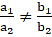 , So
, So
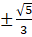

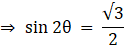
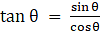

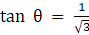
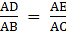

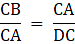

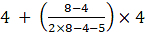
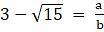 (Assume)
(Assume)
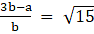
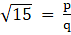
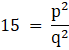
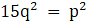
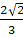 to be rational
to be rational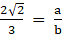 where a & b are integers (b≠0)
where a & b are integers (b≠0)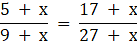
 (Given) …Equation 2
(Given) …Equation 2
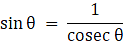
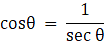


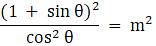
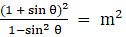
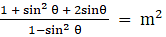
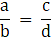
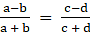
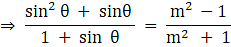
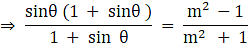
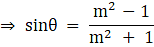
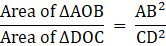
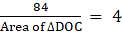
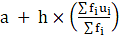
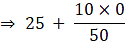

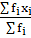

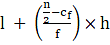

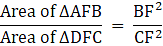

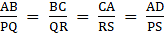 …Equation 1
…Equation 1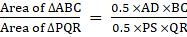 …Equation 2
…Equation 2
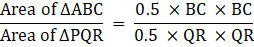
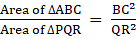


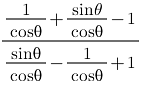 =
=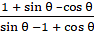
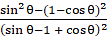

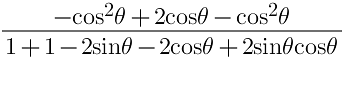
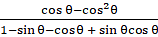
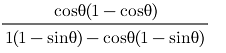
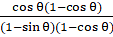
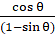
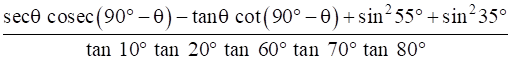


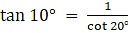
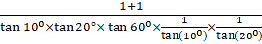
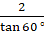
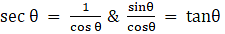 So we can write
So we can write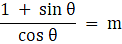
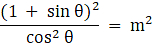
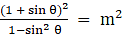
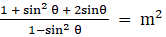
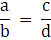
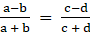
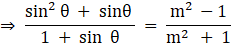
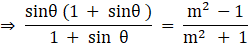




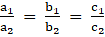 ………(i)
………(i)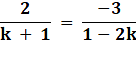
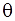 - cosec
- cosec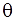 )(cos
)(cos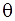 - sec
- sec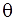 ) =
) = 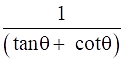
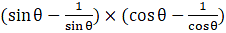
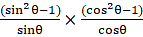
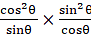

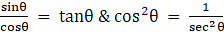
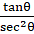
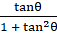
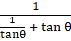
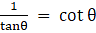
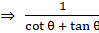 = R.H.S
= R.H.S
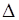 ABC is a right angled triangle right angled at C
ABC is a right angled triangle right angled at C