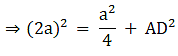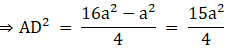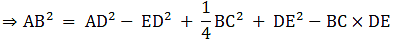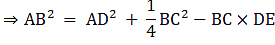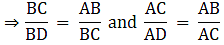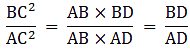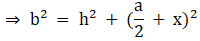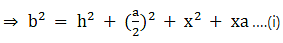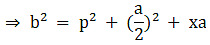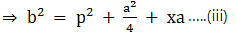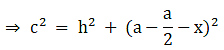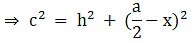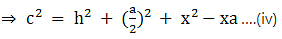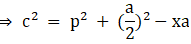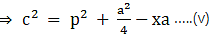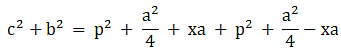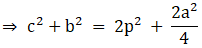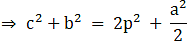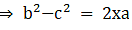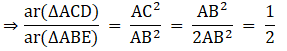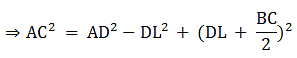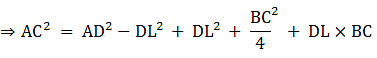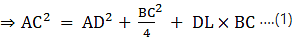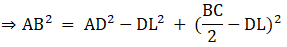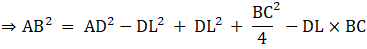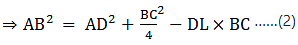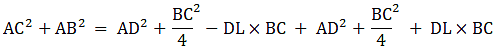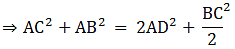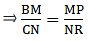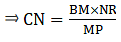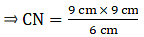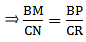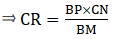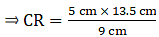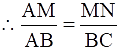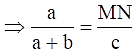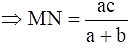RS Aggarwal Solutions: Triangles- 2 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download

Q.1. The sides of certain triangles are given below. Determine which of them are right triangles.
(i) 9 cm, 16 cm, 18 cm
(ii) 7 cm, 27 cm, 25 cm
(iii) 1.4 cm, 4.8 cm, 5 cm
(iv) 1.6 cm, 3.8 cm, 4 cm
(v) (a - 1) cm, 2 √a cm, (a + 1) cm

In a right angled triangle
(Hypotenuse)² = (Base)² + (Height)²
where hypotenuse is the longest side.
(i) L.H.S. = (Hypotenuse)² = (18)² = 324
R.H.S. = (Base)² + (Height)² = (9)² + (16)² = 81 + 256 = 337
⇒ L.H.S. ≠ R.H.S.
∴ It is not a right triangle.
(ii) L.H.S. = (Hypotenuse)² = (27)² = 729
R.H.S. = (Base)² + (Height)2 = (7)² + (25)² = 49 + 625 = 674
⇒ L.H.S. ≠ R.H.S.
∴ It is not a right triangle.
(iii) L.H.S. = (Hypotenuse)² = (5)² = 25
R.H.S. = (Base)² + (Height)² = (1.4)² + (4.8)² = 1.96 + 23.04 = 25
⇒ L.H.S. = R.H.S.
∴ It is a right triangle.
(iv) L.H.S. = (Hypotenuse)² = (4)² = 16
R.H.S. = (Base)2 + (Height)² = (1.6)² + (3.8)² = 2.56 + 14.44 = 17
⇒ L.H.S. ≠ R.H.S.
∴ It is not a right triangle.
(v) L.H.S. = (Hypotenuse)² = (a + 1)²
R.H.S. = (Base)² + (Height)² = (a-1)² + (2√a)² = a² + 1-2a + 4a = a² + 1 + 2a = (a + 1)²
⇒ L.H.S. = R.H.S.
∴ It is a right triangle.

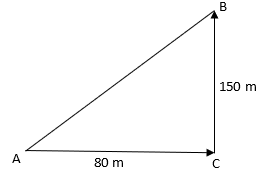
Q.2. A man goes 80 m due east and then 150 m due north. How far is he from the starting point?

The starting point of the man is A and the last point is B so we need to find AB. From the figure, ΔABC is a right triangle.
In a right angled triangle
(Hypotenuse) ² = (Base)² + (Height)²
where hypotenuse is the longest side.
(AB)² = (AC)² + (BC)²
⇒ AB² = (80)² + (150)² = 6400 + 22500 = 28900
⇒ AB = 170 m

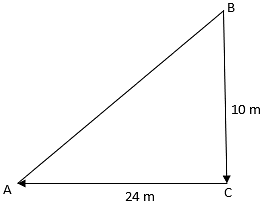
Q.3. A man goes 10 m due south and then 24 m due west. How far is he from the starting point?

The starting point of the man is B and the last point is A so we need to find AB. From the figure, ΔABC is a right triangle.
In a right angled triangle
(Hypotenuse)² = (Base)² + (Height)²
where hypotenuse is the longest side.
(AB)² = (AC)² + (BC)²
⇒ AB² = (24)² + (10)² = 576 + 100 = 676
⇒ AB = 26 m

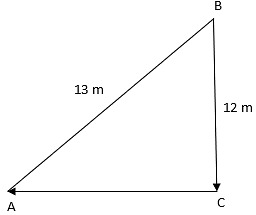
Q.4. A 13-m-long ladder reaches a window of a building 12 m above the ground. Determine the distance of the foot of the ladder from the building.

Ladder AB = 13 m and distance from the window BC = 12 m.
AC is the distance of the ladder from the building.
From the figure, ΔABC is a right triangle.
In a right angled triangle
(Hypotenuse)² = (Base)² + (Height)²
where hypotenuse is the longest side.
(AB)² = (AC)² + (BC)²
⇒13² = (AC)² + (12)²
⇒ AC² = 169- 144 = 25
⇒ AC = 5 m

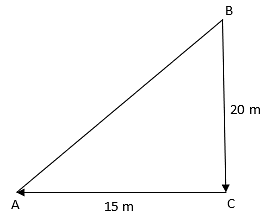
Q.5. A ladder is placed in such a way that its foot is at a distance of 15 m from a wall and its top reaches a window 20 m above the ground. Find the length of the ladder.

Ladder AB and distance from the window BC = 20 m.
AC is the distance of the ladder from the building = 15 m.
From the figure, ΔABC is a right triangle.
In a right angled triangle
(Hypotenuse)² = (Base)² + (Height)²
where hypotenuse is the longest side.
(AB)² = (AC)² + (BC)²
⇒AB² = (20)² + (15)²
⇒ AB² = 400 + 225 = 625
⇒AB = 25 m

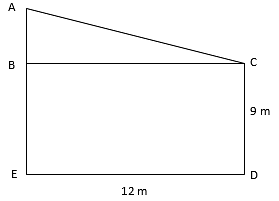
Q.6. Two vertical poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.

AE(height of the first building) = 14 m , CD(height of the second building) = 9 m , ED(distance between their feet) = BC = 12 m
AE – AB = 14 m – 9 m = 5 m
From the figure, ΔABC is a right triangle.
In a right angled triangle
(Hypotenuse)² = (Base)² + (Height)²
where hypotenuse is the longest side.
(AC)² = (AB)² + (BC)²
⇒ AC² = (5)² + (12)²
⇒ AB² = 25 + 144 = 169
⇒ AB = 13 m

Q.7. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?

Pole AB = 18 m and distance from the window BC.
AC is the length of the wire = 24 m.
From the figure, ΔABC is a right triangle.
In a right angled triangle
(Hypotenuse)² = (Base)² + (Height)²
where hypotenuse is the longest side.
(AC)² = (AB)² + (BC)²
⇒ 24² = (18)² + (BC) ²
⇒ BC² = 576 - 324 = 25²
⇒ BC = 6√7 m

Q.8. In the given figure, O is a point inside a ΔPQR such that ∠POR = 90°, OP = 6 cm and OR = 8 cm. If PQ = 24 cm and QR = 26 cm, prove that ΔPQR is right-angled.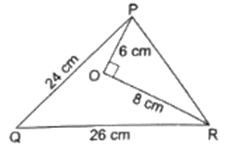

ΔPOR is a right triangle because ∠O = 90°.
In a right angled triangle
(Hypotenuse)² = (Base)² + (Height)²
where hypotenuse is the longest side.
(PR)² = (OP)² + (OR)²
⇒ PR² = (6)² + (8)²
⇒ PR² = 36 + 64 = 100
⇒ PR = 10 m
Now, PR² + PQ² = 10² + 24² = 100 + 576 = 676
Also, QR² = 26² = 676
⇒ PR² + PQ² = QR²
which satisfies Pythagoras theorem.
Hence, ∆PQR is right angled triangle.

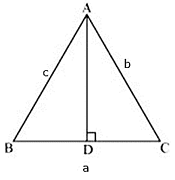
Q.9. ΔABC is an isosceles triangle with AB = AC = 13 cm. The length of altitude from A on BC is 5 cm. Find BC.

Δ ABC is an isosceles triangle.
Also, AB = AC = 13 cm
Suppose the altitude from A on BC meets BC at D. Therefore, D is the midpoint of BC.
AD = 5 cm
ΔADB and ΔADC are right-angled triangles.
Applying Pythagoras theorem,
AB² = BD² + AD²
⇒ BD² = 13² - 5²
⇒ BD² = 169 – 25 = 144
⇒ BD = 12 cm
So, BC = 2× 12 = 24 cm

Q.10. Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.

Δ ABC is an isosceles triangle.
Also, AB = AC = 2a
The AD is the altitude. Therefore, D is the midpoint of BC.
BD = a/2
ΔADB and ΔADC are right-angled triangles.
Applying Pythagoras theorem,
AB² = BD² + AD²


 

Q.11. ΔABC is an equilateral triangle of side 2a units. Find each of its altitudes.

Δ ABC is an equilateral triangle.
Also, BC = AB = AC = 2a
The AD, CE, and BF are the altitude at BC, AB and AC respectively. Therefore, D, E, and F are the midpoint of BC, AB and AC respectively.
Now, ΔADB and ΔADC are right-angled triangles.
Applying Pythagoras theorem,
AB² = BD² + AD²
⇒ (2a)² = a² + AD²
⇒ AD² = 3a²
⇒ AD = a√3 units
Similarly ΔACE and ΔBEC are right-angled triangles.
Applying Pythagoras theorem,
CE = a√3 units
And ΔABF and ΔBFC are right-angled triangles.
Applying Pythagoras theorem,
BF = a√3 units

Q.12. Find the height of an equilateral triangle of side 12 cm.

Δ ABC is an equilateral triangle.
Also, BC = AB = AC = 12 cm
The AD is the altitude at BC. Therefore, D is the midpoint of BC.
Now, ΔADB and ΔADC are right-angled triangles.
Applying Pythagoras theorem,
AB² = BD² + AD²
⇒ (12)² = 6² + AD²
⇒ AD² = 144 – 36 = 108
⇒ AD = 6√3 cm

Q.13. Find the length of a diagonal of a rectangle whose adjacent sides are 30 cm and 16 cm.

Given that AB = 30cm and AD = 16 cm
∵ ∠ A = 90°
∴ ΔADB is a right-angled triangle.
Applying Pythagoras theorem,
BD² = BA² + AD²
⇒ BD2 = 30² + 16²
⇒ BD² = 900 + 256 = 1156
⇒ BD = 34 cm
∵ Diagonals of a rectangle are equal
∴ AC = 34 cm

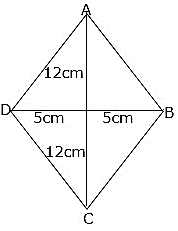
Q.14. Find the length of each side of a rhombus whose diagonals are 24 cm and 10 cm long.

ABCD is a rhombus where AC = 24 cm and BD = 10 cm.
We know that diagonals of a rhombus bisect each other at 90°.
⇒ ∠AOB = 90°, OA = 12 cm and OB = 5 cm
∴ ΔAOB is a right-angled triangle.
Applying Pythagoras theorem,
BA² = BO² + AO²
⇒ BA² = 52 + 122
⇒ BA² = 25 + 144 = 169
⇒ BA = AD = CD = BC = 13 cm
∵ Sides of a rhombus are equal.

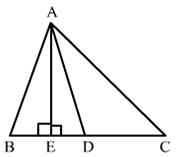
Q.15. In ΔABC, D is the midpoint of BC and AE ⊥ BC. If AC > AB, show that
AB² = AD² — BC • DE + 1/4 BC²

In right-angled triangle AED, applying Pythagoras theorem,

AB² = AE² + BE²
⇒ AE² = AB² – BE² ….(i)
In right-angled triangle AED, applying Pythagoras theorem,
AD² = AE² + ED²
⇒ AE² = AD² – ED² ….(ii)
Therefore,
AB² – BE² = AD² – ED²


 

Q.16. In the given figure, ∠ACB = 90° and CD ⊥ AB. Prove that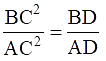

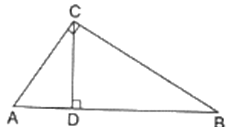
In ΔACB and ΔCDB,
∠ABC = ∠CBD (Common)
∠ACB = ∠CDB (90°)
So, by AA similarity criterion ΔACB ~ ΔCDB
Similarly, In ΔACB and ΔADC,
∠ABC = ∠ADC (Common)
∠ACB = ∠ADC (90°)
So, by AA similarity criterion ΔACB ~ ΔADC
We know that if two triangles are similar then the ratio of their corresponding sides is equal.

⇒ BC² = AB×BD ….(i)
And AC² = AB×AD …..(ii)
Dividing (i) and (ii), we get

Hence, proved.

Q.17. In the given figure, D is the midpoint of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that
(i) b² = p² + ax + a²/4
(ii) c² = p² -ax + a²/4
(iii) (b² + c²) = 2p² + 1/2 a²
(iv) (b² - c²) = 2ax

(i) ΔAEC and ΔAED are right triangles.
Applying Pythagoras theorem we get,
AC² = EC² + AE²
And AD² = ED² + AE²


And p² = h² + x² ….(ii)
Putting (ii) in (i),


Hence, proved.
(ii) ΔAEB is a right triangle.
Applying Pythagoras theorem we get,
AB² = EB² + AE²



Putting (ii) in (iv),


Hence, proved.
(iii) Adding (iii) and (v),



Hence, proved.
(iv) Subtracting (iii) and (v),


Hence, proved.

Q.18. In ΔABC, AB = AC. Side BC is produced to D. Prove that (AD² - AC²) = BD • CD.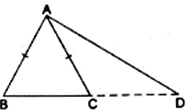

Draw AE⊥BC. Applying Pythagoras theorem in right-angled triangle AED,
Since, ABC is an isosceles triangle and AE is the altitude and we know that the altitude is also the median of the isosceles triangle.
So, BE = CE
And DE + CE = DE + BE = BD
AD² = AE² + ED²
⇒AE² = AD² - ED² …(i)
In ΔACE,
AC² = AE² + EC²
⇒ AE² = AC² –EC² …(ii)
Using (i) and (ii),
⇒ AD² - ED² = AC² –EC²
⇒ AD² - AC² = ED²–EC²
⇒ AD² - AC² = (DE + CE) (DE – CE)
⇒ AD² - AC² = (DE + BE) CD
⇒ AD² - AC² = BD.CD

Q.19. ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.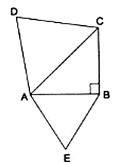

ΔABC is right triangle.
Applying Pythagoras theorem we get,
AC² = AB² + BC² {∵ AB = BC}
⇒ AC² = 2AB²
Given that the two triangles ΔACD and ΔABE are similar.
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding altitudes.

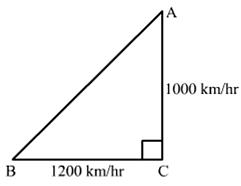
Q.20. An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 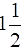 hours?

Let A be the first aeroplane flied due north at a speed of 1000 km/hr and B be the second aeroplane flied due west at a speed of 1200 km/hr
Distance covered by plane A in 1.5 hrs = 1000 × 32 = 1500km
Distance covered by plane B in 1.5 hrs = 1200 × 32 = 1800km
Now, in right triangle ABC
By using Pythagoras theorem, we have
AB² = BC² + AC²
⇒ AB² = (1800)² + (1500)²
⇒ AB² = 3240000 + 2250000
⇒ AB² = 5490000
⇒ AB = 300√61 km 

Q.21. In a ΔABC, AD is a median and AL ⊥ BC.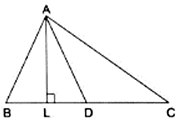

Prove that:
(a) AC² = AD² + BC • DL +
(b) AB² = AD² - BC • DL +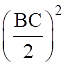
(c) AC² + AB² = 2AD² +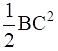

(a) In right triangle ALC
Using Pythagoras theorem, we have
AC² = AL² + LC²
⇒ AC² = AD² − DL² + (DL + DC)²



(b) In right triangle ALD
Using Pythagoras theorem, we have
AL² = AD² - LD²
Again, in ΔABL
Using Pythagoras theorem, we have
AB² = AL² + LB²
⇒ AB² = AD² –DL² + LB²
⇒ AB² = AD²–DL² + (BD – DL)²



(c) Adding (1) and (2)

Q.22. Naman is doing fly-fishing in a stream. The tip of his fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away from him and 2.4 m from the point directly under the tip of the rod. Assuming that the string (from the tip of his rod to the fly) is taut, how much string does he have out (see the adjoining figure)? If he pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from him after 12 seconds?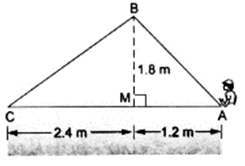

Naman pulls in the string at the rate of 5 cm per second.
Hence, after 12 seconds the length of the string he will pull is given by
12 × 5 = 60 cm or 0.6 m
Now, in ΔBMC
By using Pythagoras theorem, we have
BC² = CM² + MB²
⇒ BC² = (2.4)² + (1.8)² = 9
∴ BC = 3 m
Now, BC’ = BC – 0.6 = 3 – 0.6 = 2.4 m
Now, in ΔBC’M
By using Pythagoras theorem, we have
𝐶′𝑀² = 𝐵𝐶′²−𝑀𝐵²
⇒ C’M² = (2.4)²− (1.8)² = 2.52
∴ C’M = 1.6 m
The horizontal distance of the fly from him after 12 seconds is given by
C’A = C’M + MA = 1.6 + 1.2 = 2.8 m

Q.1. State the two properties which are necessary for given two triangles to be similar.

Two triangles are similar, if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion).

Q.2. State the basic proportionality theorem.

Basic Proportionality Theorem: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

According to the theorem:
 

Q.3. State the converse of Thales’ theorem.

Converse of Thales’ Theorem: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

According to figure above,
DE || BC.

Q.4. State the midpoint theorem.

Midpoint Theorem: The line joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.

Q.5. State the AAA-similarity criterion.

If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar. This criterion is referred to as the AAA (Angle–Angle–Angle) criterion of similarity of two triangles.

Q.6. State the AA-similarity criterion.

If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar. This is referred to as the AA-similarity criterion for two triangles.

Q.7. State the SSS-criterion for similarity of triangles.

If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar. This criterion is referred to as the SSS (Side–Side–Side)-similarity criterion for two triangles.

Q.8. State the SAS-similarity criterion.

If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar. This criterion is referred to as the SAS (Side–Angle–Side) similarity criterion for two triangles.

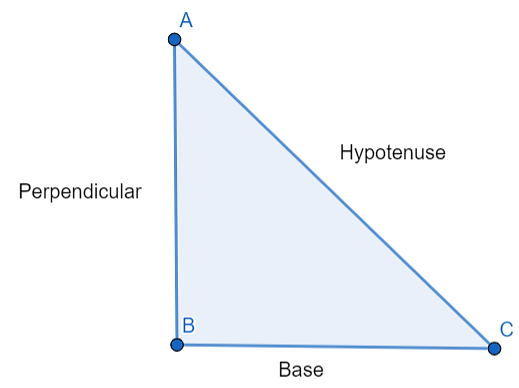
Q.9. State Pythagoras’ theorem.

In a right angled triangl Pythagoras’ Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

As shown in a right angled triangle ABC above,
(Hypotenuse)² = (Base)² + (Perpendicular)²
(AC)² = (BC)² + (AB)²

Q.10. State the converse of Pythagoras’ theorem.

Converse of Pythagoras’ Theorem: In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

Q.11. If D, E and F are respectively the midpoints of sides AB, BC and CA of ΔABC then what is the ratio of the areas of ΔDEF and ΔABC?

The figure is shown below:

We know that the midpoint theorem states that the line joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
Since D, E and F are respectively the midpoints of sides AB, BC and CA of ΔABC,
DE = AB/2; EF = BC/2; DF = AC/2
⇒ DE/AB = 1/2; EF/BC = 1/2; DF/AC = 1/2
⇒ DE/AB = EF/BC = DF/AC = 1/2 
We know that if in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar (SSS criteria).
So Δ ABC ~ Δ DEF.
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
∴ ar(Δ ABC)/ar(Δ DEF) = (AB/DE)²
⇒ ar(ΔABC)/ar(ΔDEF) = (2DE/DE)²
⇒ ar(ΔABC)/ar(ΔDEF) = (2/1)²
⇒ ar(ΔABC)/ar(ΔDEF) = (4/1)
But we need to find the ratio of the areas of ΔDEF and ΔABC.
∴ ar(ΔDEF)/ar(ΔABC) = (1/4)
∴ ar(ΔABC):ar(ΔDEF) = 1:4
1: 4

Q.12. Two triangles ABC and PQR are such that AB = 3 cm, AC = 6 cm, A = 70°, PR = 9 cm, P = 70° and PQ = 4.5 cm. Show that ΔABC ~ ΔPQR and state the similarity criterion.

We know that if one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar (SAS criteria).
Here in the given triangles, ∠A = ∠P = 70°.
And AB/PQ = AC/PR
i.e. 6/4.5 = 6/9
⇒ 2/3 = 2/3
Hence ΔABC ~ ΔPQR.
SAS-similarity

Q.13. If ΔABC ~ΔDEF such that 2AB = DE and BC = 6 cm, find EF.

Given: ΔABC ~ΔDEF such that 2AB = DE and BC = 6 cm.
From SSS-similarity criterion,
We get
AB/DE = BC/EF
Substituting the given values,
AB/2AB = 6cm/EF
1/2 = 6cm/EF
EF = 2 × 6cm
EF = 12cm
12cm

Q.14. In the given figure, DE || BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.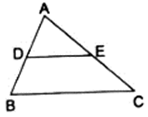

We know that the basic proportionality theorem states that
“If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.”
So if DE || BC,
Then AD/DB = AE/EC
By substituting the given values,
⇒ x cm/(3x + 4)cm = (x + 3)cm/(3x + 19)cm
Cross multiplying, we get
⇒ 3x² + 19x = 3x²+ 9x + 4x + 12
⇒ 3x² + 19x - 3x²- 9x - 4x = 12
⇒ 6x = 12
⇒ x = 2
x = 2

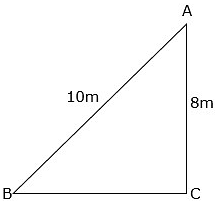
Q.15. A ladder 10 m long reaches the window of a house 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall.

Let AB be the ladder and CA be the wall with the window at A.
Let the distance of foot of ladder from base of wall BC be x.
Also, AB = 10m and CA = 8m
From Pythagoras Theorem,
we have: AB² = BC² + CA²
⇒ (10)² = x² + 8²
⇒ x² = 100 – 64
⇒ x² = 36
⇒ x = 6m
So, BC = 6m.
Length of the ladder is 6m.

Q.16. Find the length of the altitude of an equilateral triangle of side 2a cm.

Let ΔABC be the equilateral triangle whose side is 2a cm.
Let us draw altitude AD such that AD ⊥ BC.
We know that altitude bisects the opposite side.
So, BD = DC = a cm.
In ΔADC, ∠ADC = 90°.
We know that the Pythagoras Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
So, by applying Pythagoras Theorem,
AC² = AD² + DC²
(2a cm)² = AD² + (a cm)²
4a² cm² = AD² + a² cm²
AD² = 3a² cm²
AD = √3 a cm
The length of altitude is √3 a cm.

Q.17. ΔABC ~ ΔDEF such that ar(ΔABC) = 64 cm² and ar(ΔDEF) = 169 cm². If BC = 4 cm, find EF.

We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
i.e. ar(ABC)/ar(DEF) = (BC/EF)²
Substituting the given values, we get
⇒ 64cm²/169cm² = (4cm/EF cm)²
⇒ 64/169 = 16/EF²
⇒ EF² = 42.25
⇒ EF = 6.5cm
6.5 cm

Q.18. In a trapezium ABCD, it is given that AB || CD and AB = 2CD. Its diagonals AD and BC intersect at the point O such that ar (ΔA0B) = 84 cm². Find ar(ΔCOD).

Let us consider ΔAOB and ΔCOD.
∠AOB = ∠COD (∵ vertically opposite angles)
∠OBA = ∠ODC (∵ alternate interior angles)
∠OAB = ∠OCD (∵ alternate interior angles)
We know that if in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar (AAA criteria).
So, ΔAOB ≅ ΔCOD.
Given, AB = 2CD and ar(ΔAOB) = 84 cm²
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
∴ ar(ΔAOB)/ar(ΔCOD) = (AB/CD)²
⇒ 84cm²/ar(ΔCOD) = (2CD/CD)²
⇒ 84cm²/ar(ΔCOD) = 4
⇒ ar(ΔCOD) = 84cm²/4
⇒ ar(ΔCOD) = 21cm²
ar(ΔCOD) = 21cm²

Q.19. The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm², find the area of the larger triangle.

Let the smaller triangle be ΔABC and larger triangle be ΔDEF.
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
i.e. ar(ΔABC)/ar(ΔDEF) = (AB/DE)²
Substituting the given values, we get
⇒ 48cm²/ ar(ΔDEF) = (2/3)²
⇒ 48cm²/ ar(ΔDEF) = 4/9
⇒ ar(ΔDEF)= (48 × 9)/4 cm²
⇒ ar(ΔDEF) = 108cm²
108cm²

Q.20. In an equilateral triangle with side a, prove that area =

Let ΔABC be the equilateral triangle whose side is a cm.
Let us draw altitude AD(h) such that AD ⊥ BC.
We know that altitude bisects the opposite side.
So, BD = DC = a cm.
In ΔADC, ∠ADC = 90°.
We know that the Pythagoras Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
So, by applying Pythagoras Theorem,
AC² = AD² + DC²
(a cm)² = AD² + (a/2 cm)²
a² cm² = AD² + a²/4 cm²
AD² = 3a²/4 cm²
AD = √3 a/2 cm = h
We know that area of a triangle = 1/2 × base × height
Ar(ΔABC) = 1/2 × a cm × √3 a/2 cm
⇒ ar(ΔABC) = √3 a²/4 cm²
Hence proved.
ar(ΔABC) = √3 a²/4 cm²

Q.21. Find the length of each side of a rhombus whose diagonals are 24 cm and 10 cm long.

The diagonals of a rhombus bisect each other at right angles.
Let the intersecting point be O.
So, we get right angled triangles.
We know that the Pythagoras Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let us consider ΔAOB.
By Pythagoras Theorem,
AB² = AO² + OB²
AB² = 12² + 5²
AB² = 144 + 25
AB² = 169
AB = 13cm
The length of side of the rhombus is 13cm.

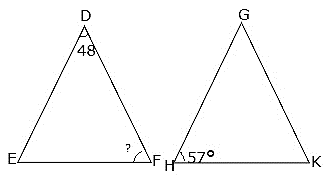
Q.22. Two triangles DEF and GHK are such that ∠D = 48° and ∠H = 57°. If ΔDEF ≅ ΔGHK then find the measure of ∠F.

Given that ΔDEF ≅ ΔGHK.

We know that if in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar (AAA criteria).
∴ ∠D = 48° = ∠G
∠H = 57° = ∠E
∠F = ∠K = x°
We know that the sum of angles in a triangle = 180°.
So, in ΔDEF,
⇒ 48° + 57° + x° = 180°
⇒ 105° + x° = 180°
⇒ x° = 180° - 105°
⇒ x° = 75° = ∠F
Ans. ∠F = 75°

Q.23. In the given figure, MN || BC and AM: MB = 1: 2.

Find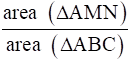

We have MN || BC,
So, ∠AMN = ∠B and ∠ANM = ∠C (Corresponding angles)
We know that if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar (AA criteria).
∴ ΔAMN ~ ΔABC.
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
i.e. ar(ΔAMN)/ ar(ΔABC) = (AM/AB)²
Given that AM: MB = 1: 2.
Since AB = AM + MB,
AB = 1 + 2 = 3.
⇒ ar(ΔAMN)/ ar(ΔABC) = (1/3)²
⇒ ar(ΔAMN)/ ar(ΔABC) = 1/9
area(ΔAMN)/ area(ΔABC) = 1/9

Q.24. In triangles BMP and CNR it is given that PB = 5 cm, MP = 6 cm, BM = 9 cm and NR = 9 cm. If ΔBMP ~ ΔCNR then find the perimeter of ΔCNR.

Given: PB = 5 cm,
MP = 6 cm,
BM = 9 cm and,
NR = 9 cm
Now, it is also given that: ΔBMP ~ ΔCNR
When two triangles are similar, then the ratios of the lengths of their corresponding sides are proportional.




⇒ CN = 54/6 = 13.5 cm.
Similarly,



⇒ CR = 7.5 cm
∴ Perimeter of ΔCNR = CN + NR+ CR = 13.5+9+7.5=30 cm

Q.25. Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.

Let ΔABC be the isosceles triangle whose sides are AB = AC = 25cm, BC = 14cm.
Let us draw altitude AD such that AD ⊥ BC.
We know that altitude bisects the opposite side.
So, BD = DC = 7cm.
In ΔADC, ∠ADC = 90°.
We know that the Pythagoras Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
So, by applying Pythagoras Theorem,
AC² = AD² + DC²
(25 cm)² = AD² + (7 cm)²
625 cm² = AD² + 49 cm²
AD² = 576 cm²
AD = 24 cm
The length of altitude is 24 cm.

Q.26. A man goes 12 m due south and then 35 m due west. How far is he from the starting point?

From ΔABC, we note that
A is the starting point.
AB = 12m, BC = 35m
CA = distance from starting point = x m
We know that the Pythagoras Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
By Pythagoras Theorem,
CA² = AB² + BC²
CA² = 12² + 35²
CA² = 144 + 1225
CA² = 1369
CA = 37m
The man is 37 m far from the starting point.

Q.27. If the lengths of the sides BC, CA and AB of a ΔABC are a, b and c respectively and AD is the bisector of ∠A then find the lengths of BD and DC.

Given that ΔABC is the triangle whose sides are AB = c, AC = b, BC = a
And AD is the bisector of ∠A.
We know that altitude bisects the opposite side.
So, let BD = DC = x.
Since AD bisects ∠A,
AC/AB = CD/DB
Substituting the given values,
b/c = CD/(a-CD)
Cross multiplying,
⇒ b( a – CD) = c (CD)
⇒ ba – b(CD) = c (CD)
⇒ ba = CD (b + c)
⇒ CD = ba/ (b + c)
Since CD = BD,
BD = ba/ (b + c)
BD = ba/(b + c) and DC = ba/(b + c)

Q.28. In the given figure, ∠AMN = ∠MBC = 76°. If a, b and c are the lengths of AM, MB and BC respectively then express the length of MN in terms of a, b and c.

In ΔAMN and ΔABC
∠AMN = ∠ABC = 76° (Given)
∠A = ∠A (common)
By AA Similarity criterion, ΔAMN ~ Δ ABC
If two triangles are similar, then the ratio or the their corresponding sides are proportional

Q.29. The lengths of the diagonals of a rhombus are 40 cm and 42 cm. Find the length of each side of the rhombus.

The diagonals of a rhombus bisect each other at right angles.
Let the intersecting point be O.
So, we get right angled triangles.
We know that the Pythagoras Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let us consider ΔAOB.
By Pythagoras Theorem,
AB² = AO² + OB²
AB² = 21² + 20²
AB² = 441 + 400
AB² = 841
AB = 29cm
The length of each side of the rhombus is 29cm.

Q.30. For each of the following statements state whether true (T) or false (F):
(i) Two circles with different radii are similar.
(ii) Any two rectangles are similar.
(iii) If two triangles are similar then their corresponding angles are equal and their corresponding sides are equal.
(iv) The length of the line segment joining the midpoints of any two sides of a triangle is equal to half the length of the third side.
(v) In a ΔABC, AB = 6 cm, ∠A = 45° and AC = 8 cm and in a ΔDEF, DF = 9 cm, ∠D = 45° and DE = 12 cm, then ΔABC ~ ΔDEF.
(vi) The polygon formed by joining the midpoints of the sides of a quadrilateral is a rhombus.
(vii) The ratio of the areas of two similar triangles is equal to the ratio of their corresponding angle-bisector segments.
(viii) The ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding medians.
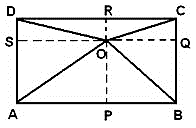
(ix) If O is any point inside a rectangle ABCD then OA² + OC² = OB² + OD².
(x) The sum of the squares on the sides of a rhombus is equal to the sum of the squares on its diagonals.

(i) T
Two similar figures have the same shape but not necessarily the same size. Therefore, all circles are similar.
(ii) F
Two polygons of the same number of sides are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportion).
Consider an example,
Let a rectangle have sides 2cm and 3cm and another rectangle have sides 2cm and 5cm.
Here, the corresponding angles are equal but the corresponding sides are not in the same ratio.
(iii) F
Two triangles are similar, if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion).
(iv) T
Midpoint Theorem states that the line joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
(v) F
Two triangles are similar, if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion).
But here, the corresponding sides are
AB/DE = 6/12 = 1/2 and AC/DF = 8/9
AB/DE ≠ AC/DF
(vi) F
The polygon formed by joining the midpoints of sides of any quadrilateral is a parallelogram.
(vii) T
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
(viii) T
The perimeters of the two triangles are in the same ratio as the sides. The corresponding medians also will be in this same ratio.
(ix) T

Let us construct perpendiculars OP, OQ, OR and OS from point O.
Let us take LHS = OA² + OC²
From Pythagoras theorem,
= (AS² + OS²) + (OQ² + QC²)
As also AS = BQ, QC = DS and OQ = BP = OS,
= (BQ² + OQ²) + (OS² + DC²)
Again by Pythagoras theorem,
= OB² + OD² = RHS
As LHS = RHS, hence proved.
(x) T

In rhombus ABCD, AB = BC = CD = DA.
We know that diagonals of a rhombus bisect each other perpendicularly.
i.e. AC ⊥ BD, ∠AOB = ∠BOC = ∠COD = ∠AOD = 90° and
OA = OC = AC/2, OB = OD = BD/2
Let us consider right angled triangle AOB.
By Pythagoras theorem,
AB² = OA² + OB²
⇒ AB² = (AC/2)² + (BD/2)²
⇒ AB² = AC²/4 + BD²/4
⇒ 4AB² = AC²+ BD²
⇒ AB² + AB² + AB² + AB² = AC²+ BD²
∴ AB² + BC² + CD² + DA² = AC²+ BD²