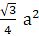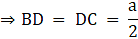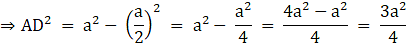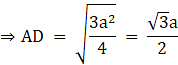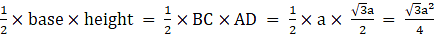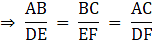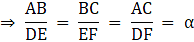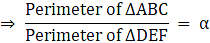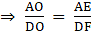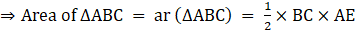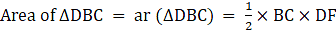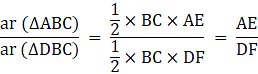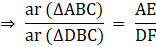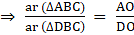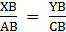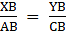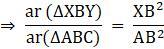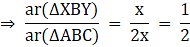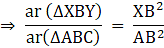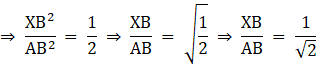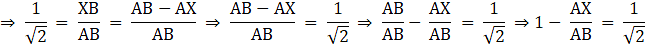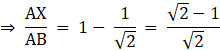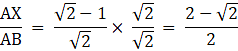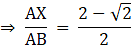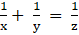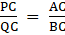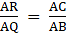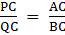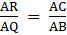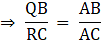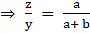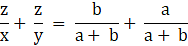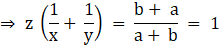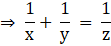RS Aggarwal Solutions: Triangles- 4 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
Formative Assessment (unit Test)
Q.1. ΔABC ~ ΔDEF and their perimeters are 32 cm and 24 cm respectively. If AB = 10 cm then DE = ?
(a) 8 cm
(b) 7.5 cm
(c) 15 cm
(d) 5√3 cm
Given: ∆ABC ∼ ∆DEF
Perimeter of ∆ABC = 32 cm
Perimeter of ∆DEF = 24 cm
AB = 10 cm
To find: DE
∵ ∆ABC ∼ ∆DEF
∴ The ratio of the corresponding sides of ∆ ABC and ∆ DEF are equal to the ratio of the perimeter of the corresponding triangles.
Q.2. In the given figure, DE || BC. If DE = 5 cm, BC = 8 cm and AD = 3.5 cm then AB = ?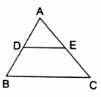
(a) 5.6 cm
(b) 4.8 cm
(c) 5.2 cm
(d) 6.4 cm
Given: DE ∥ BC
DE = 5 cm
BC = 8 cm
AD = 3.5 cm
To find: AB
∵ DE ∥ BC
∴ By Basic proportionality theorem, we have...(i)
Now, in ∆ ADE and ∆ ABC, we have[By (i)]
∠DAE = ∠BAC [Common angle]
∴ By SAS criterion,
∆ ADE ∼ ∆ ABC
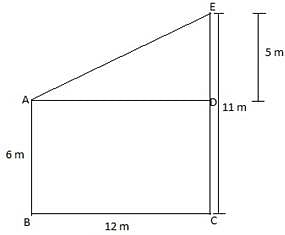
Q.3. Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their feet is 12 m then the distance between their tops is
(a) 12 m
(b) 13 m
(c) 14 m
(d) 15 m
Given: Height of pole 1 = 6 m
Height of pole 2 = 11 m
Distance between the feet of pole 1 and pole 2 = 12 m
To find: Distance between the tops of both the poles
Clearly, In ∆ ADE,
DE = 5 m
AD = 12 m
Also, ∠ADE = 90° [∵ Both the poles stand vertically upright]
∴ By applying Pythagoras theorem, we have
AE2 = AD2 + DE2
⇒ AE2 = (12)2 + (5)2 = 144 + 25 = 169
⇒ AE = √169 = 13 m
Q.4. The areas of two similar triangles are 25 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 3.5 cm then the corresponding altitude of the other triangle is
(a) 5.6 cm
(b) 6.3 cm
(c) 4.2 cm
(d) 7 cm
Given: Area of triangle 1 = 25 cm2
Area of triangle 2 = 36 cm2
Altitude of triangle 1 = 3.5 cm
To find: Altitude of triangle 2
Let the altitude of triangle 2 be x.
∵ The areas of two similar triangles are in the ratio of the squares of the corresponding altitudes.
∴ We have,
⇒ x = √17.64 = 42 cm
Q.5. If ΔABC ~ ΔDEF such that 2AB = DE and BC = 6 cm, find EF.
Given: ∆ABC ∼ ∆DEF
2AB = DE ….(i)
BC = 6 cm
To find: EF
∵ ∆ABC ∼ ∆DEF
∴ Ratio of all the corresponding sides of ∆ ABC and ∆ DEF are equal.….(ii)
Also, from (i), we have
2AB = DE….(iii)
[By (ii) and (iii)]
Q.6. In the given figure, DE || BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.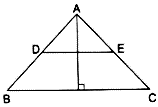
Given: DE ∥ BC
AD = x cm
DB = (3x + 4) cm
AE = (x + 3) cm
EC = (3x + 19) cm
To find: x
∵ DE ∥ BC
∴ By Basic Proportionality theorem, we have
⇒ x (3x + 19) = (x + 3) (3x + 4)
⇒ 3x2 + 19x = 3x2 + 13x + 12
⇒ 19x – 13x = 3x2 + 12 – 3x2
⇒ 6x = 12 or x = 2
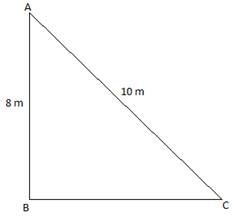
Q.7. A ladder 10 m long reaches the window of a house 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall.
Given: Height of the window from the ground = 8 m
Length of the ladder = 10 m
To find: Distance of the foot of the ladder from the base of the wall.
Consider the following diagram corresponding to the question.
Here, AB = Height of the window form the ground = 8 m
AC = Length of the ladder = 10 m
BC = Distance of the foot of the ladder from the base of the wall
Now, in ∆ ABC,
By Pythagoras theorem, we have
AC2 = AB2 + BC2
⇒ BC2 = AC2 – AB2
⇒ BC2 = (10)2 – (8)2 = 100 – 64 = 36
⇒ BC = √36 = 6 m
Q.8. Find the length of the altitude of an equilateral triangle of side 2a cm.
Given: Side of equilateral triangle = 2a cm
To find: Length of altitude
Let ∆ ABC be an equilateral triangle with side 2a cm.
Let AD be the altitude of ∆ ABC.
Here, BD = DC = a
In ∆ ABD,
Using Pythagoras theorem, we have
AB2 = AD2 + BD2⇒ AD2 = AB2 – BD2⇒ AD2 = (2a)2 – (a)2 = 4a2 – a2 = 3a2
⇒ AD2 = 3a2
⇒ AD = √3a2 = √3 a cm
Q.9. ΔABC ~ ΔDEF such that ar (ΔABC) = 64 cm2 and ar(ΔDEF) = 169 cm2. If BC = 4 cm, find EF.
Given: ∆ ABC ∼ ∆ DEF
ar (∆ ABC) = 64 cm2, ar (∆ DEF) = 169 cm2
BC = 4 cm
To find: EF
∵ The ratios of the areas of two similar triangles are equal to the ratio of squares of any two corresponding sides.
∴ We have
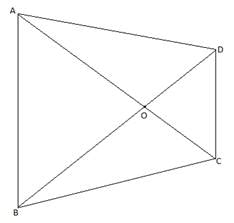
Q.10. In a trapezium ABCD, it is given that AB || CD and AB = 2CD. Its diagonals AC and BD intersect at the point 0 such that ar (ΔAOB) = 84 cm2. Find ar (ΔCOD).
Given: AB ∥ CD
AB = 2CD ….(i)
ar (∆ AOB) = 84 cm2
To find: ar (∆ COD)
In ∆ AOB and ∆ COD,
∠ AOB = ∠ COD [Vertically Opposite angles]
∠ OAB = ∠ OCD [Alternate interior angles (AB ∥ CD)]
∠ OBA = ∠ ODC [Alternate interior angles (AB ∥ CD)]
⇒ ∆ AOB ∼ ∆ COD [By AAA criterion]
Now,
∵ The ratios of the areas of two similar triangles are equal to the ratio of squares of any two corresponding sides.
∴ We have
Also, from (i), we have
Q.11. The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
Given: Let the smaller triangle be ∆ ABC and the larger triangle be ∆ DEF.
The ratio of AB and DE = 2 : 3….(i)
ar (∆ ABC) = 48 cm2
To find: ar (∆ DEF)
∵ The ratios of the areas of two similar triangles are equal to the ratio of squares of any two corresponding sides.
∴ We have
Q.12. In the given figure, LM || CB and LN || CD. Prove that 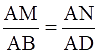
Given: LM ∥ CB and LN ∥ CD
To prove:
In ∆ AML, LM ∥ CB
∴ By Basic proportionality theorem, we have….(i)
In ∆ ALN, LN ∥ CD
∴ By Basic proportionality theorem, we have….(ii)
By (i) and (ii), we have
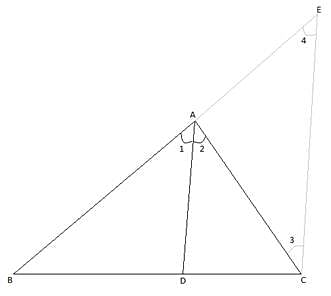
Q.13. Prove that the internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
Given: ∆ ABC with the internal bisector AD of ∠A which intersects BC at D.
To prove:
First, we construct a line EC ∥ AD which meets BA produced in E.
Now, we have
CE ∥ DA ⇒ ∠2 = ∠3 [Alternate interior angles are equal (transversal AC)]
Also, ∠1 = ∠4 [Corresponding angles are equal (transversal AE)]
We know that AD bisects ∠A ⇒ ∠1 = ∠2
⇒ ∠4 = ∠1 = ∠2 = ∠3
⇒ ∠3 = ∠4
⇒ AE = AC [Sides opposite to equal angles are equal] ….(i)
Now, consider ∆ BCE,
AD ∥ EC[By Basic Proportionality theorem]
[∵ BA = AB and AE = AC (From (i))]
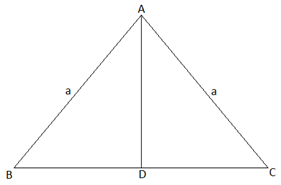
Q.14. In an equilateral triangle with side a, prove that area = 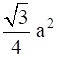 .
.
Let ∆ ABC be an equilateral triangle with side a.
To prove: Area of ∆ ABC =
In ∆ ABC, AD bisects BC
Now, in ∆ ACD
Using Pythagoras theorem,
AC2 = AD2 + DC2
⇒ AD2 = AC2 – DC2
Now, in ∆ ABC
Area of ∆ ABC =
Q.15. Find the length of each side of a rhombus whose diagonals are 24 cm and 10 cm long.
Given: Length of one of the diagonals = 24 cm
Length of the other diagonal = 10 cm
To find: Length of the side of the rhombus
∵ The length of all sides of rhombus is equal.
∴ Let side of rhombus ABCD be x cm.
Also, we know that the diagonals of a rhombus are perpendicular bisectors of each other.
⇒ AO = OC = 12 cm and BO = OD = 5 cm
Also, ∠AOB = ∠BOC = ∠COD = ∠AOD = 90°
Now, consider ∆ AOD
AO = 12 cm and OD = 5 cm
∠AOD = 90°
So, using Pythagoras theorem, we have
AD2 = AO2 + OD2 = 122 + 52 = 144 + 25 = 169
⇒ AD = √169 = 13 cm
Q.16. Prove that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.
Let ∆ ABC and ∆ DEF be two similar triangles, i.e., ∆ ABC ∼ ∆ DEF.
⇒ Ratio of all the corresponding sides of ∆ ABC and ∆ DEF are equal.
Let these ratios be equal to some number α.
⇒ AB = α DE, BC = α EF, AC = α DF ….(i)
Now, perimeter of ∆ ABC = AB + BC + AC
= α DE + α EF + α DF [ From (i)]
= α (DE + EF + DF)
= α (perimeter of ∆ DEF)
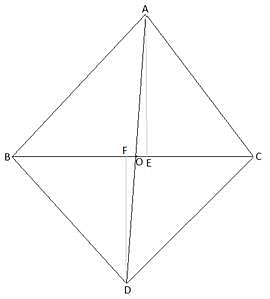
Q.17. In the given figure, ΔABC and ΔDBC have the same base BC. If AD and BC intersect at O, prove that 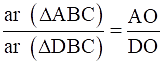
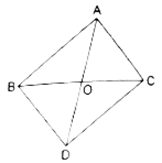
Given: ∆ ABC and ∆ DBC have the same base BC.
AD and BC intersect at O.
To show:
First, we construct the altitudes, AE and DF, of ∆ ABC and ∆ DBC, respectively.
Consider, ∆ AOE and ∆ DOF,
∠DFO = ∠AEO [Right angles]
∠DOF = ∠AOE [Vertically Opposite angles]
So, by AA criterion,
∆AOE ∼ ∆DOF
⇒ Ratio of all the corresponding sides of ∆ AOE and ∆ DOF are equal.….(i)
Now, we know that….(ii)
Similarly,….(iii)
Dividing (ii) by (iii),[From (i)]
Q.18. In the given figure, XY || AC and XY divides ΔABC into two regions, equal in area. Show 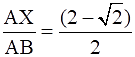
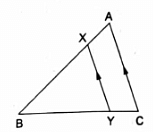
Given: XY ∥ AC
ar (∆ XBY) = ar (XACY) ….(i)
To show:
Consider ∆ ABC, XY ∥ AC
So, Using Basic Proportionality theorem, we have….(ii)
Now, in ∆ XBY and ∆ ABC,
∠XBY = ∠ABC [common angle][Using (ii)]
⇒ ∆ XBY ∼ ∆ ABC [By SAS criterion]
Now, we know that the ratios of the areas of two similar triangles are equal to the ratio of squares of any two corresponding sides.
From (i), we have
ar (∆ XBY) = ar (XACY)
Let ar (∆ XBY) = x = ar (XACY) ⇒ ar (∆ ABC) = ar (∆ XBY) + ar (XACY) = x + x = 2x
Now, we know that
XB = AB – AX
Rationalizing the denominator, we have
Q.19. In the given figure, ΔABC is an obtuse triangle, obtuse-angled at B. If AD ⊥ CB (produced) prove that AC2 = AB2 + BC2 + 2BC • BD.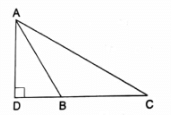
Given: AD ⊥ CB (produced)
To prove: AC2 = AB2 + BC2 + 2BC • BD
In ∆ ADC, DC = DB + BC ….(i)
First, in ∆ ADB,
Using Pythagoras theorem, we have
AB2 = AD2 + DB2⇒ AD2 = AB2 – DB2 ….(ii)
Now, applying Pythagoras theorem in ∆ ADC, we have
AC2 = AD2 + DC2
= (AB2 – DB2) + DC2 [Using (ii)]
= AB2 – DB2 + (DB + BC)2 [Using (i)]
Now, ∵ (a + b)2 = a2 + b2 + 2ab
∴ AC2 = AB2 – DB2 + DB2 + BC2 + 2DB • BC
⇒ AC2 = AB2 + BC2 + 2BC • BD
Q.20. In the given figure, each one of PA, QB and RC is perpendicular to AC. If AP = x, QB = z, RC = y, AB = a and BC = b, show that 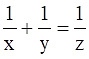 .
. 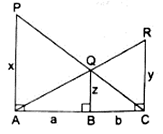
Given: PA ⊥ AC, QB ⊥ AC and RC ⊥ AC
AP = x, QB = z, RC = y, AB = a and BC = b
To show:
In ∆ PAC, we have
QB ∥ PA
So, by Basic Proportionality theorem, we have….(i)
In ∆ ARC, we have
QB ∥ RC
So, by Basic Proportionality theorem, we have….(ii)
Now, Consider ∆ PAC and ∆ QBC,
∠PCA = ∠QCB [Common angle][By (i)]
So, by SAS criterion,
∆ PAC ∼ ∆ QBC
⇒ Ratio of all the corresponding sides of ∆ ABC and ∆ DEF are equal.….(iii)
Now, consider ∆ ARC and ∆ AQB,
∠RAC = ∠QAB [Common angle][By (ii)]
So, by SAS criterion,
∆ ARC ∼ ∆ AQB
⇒ Ratio of all the corresponding sides of ∆ ARC and ∆ AQB are equal.….(iv)
Now, adding (iii) and (iv), we get
|
53 docs|15 tests
|
|
53 docs|15 tests
|

|
Explore Courses for Class 10 exam
|

|
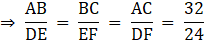
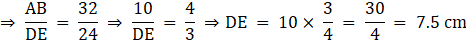
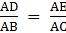
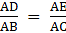
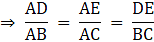
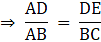
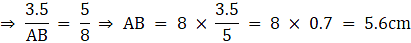
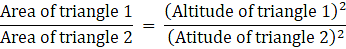

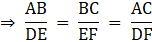
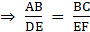
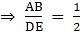
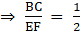
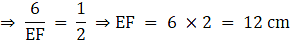
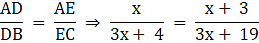

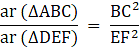
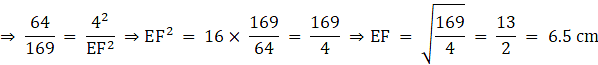
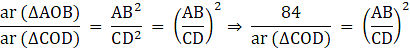
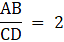
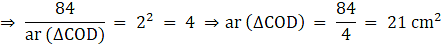
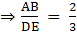
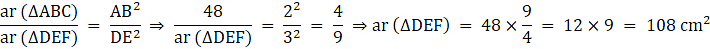
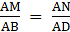
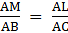
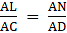
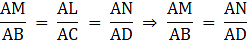
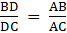
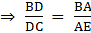 [By Basic Proportionality theorem]
[By Basic Proportionality theorem]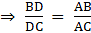 [∵ BA = AB and AE = AC (From (i))]
[∵ BA = AB and AE = AC (From (i))]