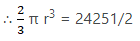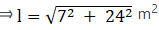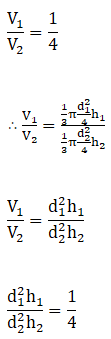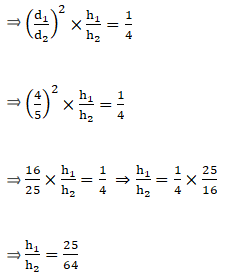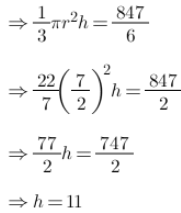RS Aggarwal Solutions: Volume and Surface Area of Solids- 1 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download

Q.1. Two cubes each of volume 27 cm³ are joined end to end to form a solid. Find the surface area of the resulting cuboid.

Let the length of the side of cube be ‘a’ cm.
Volume of each cube = 27 cm³
Volume of cube = a³
∴ a³ = 27 cm³
⇒ a = (27 cm³)^1/3
⇒ a = 3 cm
Length of a side of cube = 3 cm
Since, two cubes are joined and a cuboid is formed so,

Length of cuboid = l = 2a = 2 × 3 cm = 6 cm
Breadth of cuboid = b = a = 3 cm
Height of cuboid = h = a = 3 cm
Surface area of cuboid = 2 × (l × b + b × h + l × h)
∴ Surface area of resulting cuboid = 2 × (6 × 3 + 3 × 3 + 6 × 3) cm²
= 2 × (18 + 9 + 18) cm²
= 2 × 45 cm²
= 90 cm²
So, surface area of resulting cuboid is 90 cm²

Q.2. The Volume of a hemisphere is 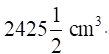 Find its curved surface area.

Let the radius of hemisphere be r cm
Volume of hemisphere is given by (2/3)πr³
Given, volume of hemisphere = 24251/2 cm³

⇒ r³ = 4851 × 1/2 × 3/2 × 7/22
⇒ r³ = 1157.625 cm³
⇒ r = (1157.625)^1/3 cm
⇒ r = 10.5 cm
Curved Surface Area of hemisphere = 2πr²
Curved Surface Area of hemisphere = 2 × 22/7 × (10.5)² cm²
= 693 cm²
∴ Curved surface area of hemisphere = 693 cm².

Q.3. If the total surface area of a solid hemisphere is 462 cm², find its volume.

Let the radius of solid sphere be r cm
Total surface area of solid hemisphere = 3πr²
Given, total surface area of solid hemisphere = 462 cm²
∴ 3πr² = 462 cm²
⇒ 3 × 22/7 × r² = 462 cm²
⇒ r² = 462 × 1/3 × 7/22 cm² = 49 cm²
⇒ r = 7 cm
Volume of solid hemisphere = 4/3πr³
= 2/3 × 22/7 × 7³ cm³
= 718.67 cm³
∴ Volume of solid hemisphere is 718.67 cm³

Q.4. A 5-m-wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of Rs 25 per metre.

Width of cloth used = 5 m
Diameter of conical tent to be made = 14 m
Let the radius of the conical tent be r m
Radius of conical tent = r = diameter ÷ 2 = 14/2 m = 7 m
Height of conical tent = h = 24 m
Let the slant height of conical tent be l
So,

⇒ l = 25 m
Area of cloth required to make a conical tent = Curved Surface area of conical tent
= πrl
= 22/7 × 7 × 25 m²
= 550 m²
Length of cloth used = Area of cloth required ÷ width of cloth
= 550/5 m
= 110 m
∴ Length of cloth used = 110 m
Cost of cloth used = Rs 25 per meter
Total Cost of cloth required to make a conical tent = 110 × Rs 25
= Rs 2750
∴ Total cost of cloth required to make a conical tent = Rs 2750

Q.5. If the volumes of two cones are in the ratio of 1 : 4 and their diameters are in the ratio of 4 : 5, find the ratio of their heights.

Let V₁ be the volume of first cone and V₂ be the volume of second cone.
Then, V₁:V₂ = 1:4
Let d₁ be the diameter of first cone and d₂ be the diameter of second cone.
Then d₁:d₂ = 4:5
Let h₁ be the height of first cone and h₂ be the height of second cone.
We know that volume of cone is given by V = 1/3 × π(d²/4)h


∴ h₁:h₂ = 25:64
∴ Ratio of height of two cones is 25:64.

Q.6. The slant height of a conical mountain is 2.5km and the area of its base is 1.54 km2. Find the height of mountain.

Let the radius of base be ‘r’ km and slant height be ‘l’ km
Slant height of conical mountain = 2.5 km
Area of its base = 1.54 km²
Area of base is given by πr²
∴ πr² = 1.54 km²
⇒ 22/7 × r² = 1.54 km²
⇒ r² = 1.54 × 7/22 km² = .49 km²
⇒ r = 0.7 km
Let ‘h’ be the height of the mountain
We know,
l² = r² + h²
Substituting the values of l and r in the above equation
2.5² = 0.7² + h²
h² = 2.5² – 0.7² = 6.25 – 0.49 km²
h² = 5.76 km²
h = 2.4 km
∴ Height of the mountain = 2.4 km

Q.7. The Sum of the radius of the base and the height of a solid cylinder is 37 metres. If the total surface area of the cylinder be 1628sq metres, find its volume.

Let the Radius of the solid cylinder be ‘r’ m and its height be ‘h’ m.
Given,
Sum of radius and height of solid cylinder = 37 m
r + h = 37 m
r = 37 – h
Total surface area of solid cylinder = 1628 m²
Total surface area of solid cylinder is given by 2πr (h + r)
∴ 2πr (h + r) =1628 m²
Substituting the value of r + h in the above equation
⇒ 2πr × 37 = 1628 m²
⇒ r = 1628 × 7/22 × 1/2 × 1/37 m
⇒ r = 7 m
Since, r + h = 37 m
h = 37 – r m
h = 37 – 7 m = 30 m
Volume of solid cylinder = πr²h
= 22/7 × 7² × 30 m²
= 4620 m²

Q.8. The surface area of a sphere is 2464 cm². If its radius be doubled, what will be the surface area of the new sphere?

Let the radius of sphere be ‘r’ cm
Surface area of sphere = 2464 cm²
Surface area of sphere is given by 4πr²
∴ 4πr² = 2464 cm²
⇒ 4 × 22/7 × r² = 2464 cm²
⇒ r² = 2464 × 1/4 × 7/22 cm² = 196 cm²
⇒ r = 14 cm
Radius of new sphere is double the radius of given sphere.
Let the radius of new sphere be r’ cm
∴ r’ = 2r
r’ = 2 × 14 cm = 28 cm
Surface area of new sphere = 4πr’²
= 4 × 22/7 × 28² cm²
= 9856 cm²
∴ Surface area of new sphere is 9856 cm².

Q.9. A military tent of height 8.25m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of a same base radius. Find the length of canvas used in making the tent, if the breadth of the canvas is 1.5 m.

The military tent is made as a combination of right circular cylinder and right circular cone on top.
Total Height of tent = h = 8.25 m
Base diameter of tent = 30 m
Base radius of tent = r = 30/2 m = 15 m
Height of right circular cylinder = 5.5 m
Curved surface area of right circular cylindrical part of tent = 2πrh
Height of conical part = total height of tent – height of cylindrical part
hcone = 8.25 – 5.5 m = 2.75 m
Base radius of cone = 15 m
Let l be the slant height of cone
Then, l² = h_cone² + r² = 2.75² + 15² m²
l² = 7.5625 + 225 m² = 232.5625
l = 15.25
Curved surface area of conical part of the tent = πrl
Total surface area of the tent = Curved surface area of cylindrical part + curved surface area of conical part
Total surface area of tent = 2πrh + πrl
= πr (2h + l)
= 22/7 × 15 × (2 × 5.5 + 15.25) m²
= 22/7 × 15 × (11 + 15.25) m²
= 22/7 × 15 × 26.25 m²
= 1237.5 m²
Breadth of canvas used = 1.5 m
Length of canvas used = Total surface area of tent ÷ breadth of canvas used
Length of canvas used = 1237.5\1.5 m = 825 m
∴ Length of canvas used is 825 m.

Q.10. A tent is in the shape of a right circular cylinder up to a height of 3 m and conical above it. The total height of the tent is 13.5 m and the radius of its base is 14 m. Find the cost of cloth required to make the tent at the rate of Rs 80 per square metre. [Take π = 22/7.]

The tent is made as a combination of right circular cylinder and right circular cone on top.
Height of cylindrical part of the tent = h = 3 m
Radius of its base = r = 14 m
Curved surface area of cylindrical part of tent = 2πrh
= 2 × 22/7 × 14 × 3 m²
= 264 m²
Total height of the tent = 13.5 m
Height of conical part of the tent = total height of tent – height of cylindrical part.
Height of conical part of the tent = 13.5 – 3 m =10.5 m
Let the slant height of the conical part be l
l² = h_cone² + r²
l² = 10.5² + 14² = 110.25 + 196 m² = 306.25 m²
l = 17.5 m
Curved surface area of conical part of tent = πrl
= 22/7 × 14 × 17.5 m²
= 770 m²
Total surface area of tent = Curved surface area of cylindrical part of tent + Curved surface area of conical part of tent
Total Surface area of tent = 264 m² + 770 m² = 1034 m²
Cloth required = Total Surface area of tent = 1034 m²
Cost of cloth = Rs 80/m²
Total cost of cloth required = Total surface area of tent × Cost of cloth
= 1034 × Rs 80
= Rs 82720
Cost of cloth required to make the tent is Rs 82720.

Q.11. A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and the slant height of the conical portion is 53 m, find the area of canvas needed to make the tent. [Take π = 22/7.]

The Circus tent is made as a combination of cylinder and cone on top.
Height of cylindrical part of tent = h = 3 m
Base radius of tent = r = 52.5 m
Area of canvas required for cylindrical part of tent = 2πrh
= 2 × 22/7 × 52.5 × 3 m²
= 990 m²
Slant height of cone = l = 53 m
Area of canvas required for conical part of the tent = πrl
= 22/7 × 52.5 × 53 m²
= 8745 m²
Area of canvas required to make the tent = Area of canvas required for cylindrical part of tent + Area of canvas required for conical part of tent
Area of canvas required to make the tent = 990 + 8745 m² = 9735 m²

Q.12. A rocket is in the form of a circular cylinder closed at the lower and a cone of the same radius is attached to the top. The radius of the cylinder is 2.5 m, its height is 21 m and the slant height of the cone is 8 m. Calculate the total surface area of the rocket.

The rocket is in the form of cylinder closed at the bottom and cone on top.
Height of cylindrical part rocket = h = 21 m
Base radius of rocket = r = 2.5 m
Surface Area of cylindrical part of rocket = 2πrh + πr²
= 2 × 22/7 × 2.5 × 21 + 22/7 × 2.5 × 2.5 m²
= 330 + 19.64 m² = 349.64 m²
Slant height of cone = l = 8 m
Surface Area of conical part of the rocket = πrl
= 22/7 × 2.5 × 8 m²
= 62.86 m²
Total surface area of the rocket = Surface Area of cylindrical part of rocket + Surface Area of conical part of rocket
Total surface area of the rocket = 349.64 + 62.86 m² = 412.5 m².

Q.13. A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them being 3.5 cm and the total height of the solid is 9.5 cm. Find the volume of the solid.

The solid is in the form of a cone surmounted on a hemisphere.
Total height of solid = h = 9.5 m
Radius of Solid = r = 3.5 m
Volume of hemispherical part solid = 2/3 × πr³
= 2/3 × 22/7 × 3.53 m³
= 89.83 m³
Height of conical part of solid = h_cone = Total height of solid – Radius of solid
Height of conical part of solid = h_cone = 9.5 – 3.5 = 6 m
Volume of conical part of solid = 1/3 × πr²h_cone
= 1/3 × 22/7 × 3.5² × 6 m³
= 77 m³
Volume of solid = Volume of hemispherical part solid + Volume of conical part solid
Volume of solid = 89.83 + 77 m³ = 166.83 m³

Q.14. A toy is in the form of a cone mounted on a hemisphere of same radius 7 cm. If the total height of the toy is 31 cm, find its total surface area.

The toy is in the form of a cone mounted on a hemisphere.
Total height of toy = h = 31 cm
Radius of toy = r = 7 cm
Surface area of hemispherical part toy = 2πr²
= 2 × 22/7 × 7² cm²
= 308 cm²
Height of conical part of toy = h_cone = Total height of toy – Radius of toy
Height of conical part of toy = h_cone = 31 – 7 = 24 cm
Let the slant height of the conical part be l
l² = h_cone² + r²
l² = 24² + 7² = 576 + 49 cm² = 625 cm²
l = 25 cm
Surface area of conical part of toy = πrl
= 22/7 × 7 × 25 cm²
= 550 cm²
Total surface area of toy = Surface area of hemispherical part of toy + Surface area of conical part of toy
Total Surface area of toy = 308 cm² + 550 cm² = 858 cm²

Q.15. A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm³ and its diameter is 7 cm, find the height of the toy.

A toy is in the shape of a cone mounted on a hemisphere of same base radius.
Volume of Toy = 231 cm³
Base Diameter of toy = 7 cm
Base radius of toy = 7/2 cm = 3.5 cm
Volume of hemisphere = 2/3 πr³
= 2/3 × 22/7 × 3.5³ cm³

= 539/6
Volume of cone = Volume of hemisphere – Volume of toy

Volume of cone is given by 1/3 πr²h
Where h is the height of cone

Height of cone = 11 cm
Height of toy = Height of cone + Height of hemisphere
= 11 cm + 3.5 cm = 14.5 cm
[Height of hemisphere = Radius of hemisphere]
∴ Height of toy is 14.5 cm.

Q.16. A cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is 4 times the radius of its base, find the radius of the ice-cream cone.

Radius of cylindrical container = r = 6 cm
Height of cylindrical container = h = 15 cm
Volume of cylindrical container = πr²h
= 22/7 × 6 × 6 × 15 cm³
= 1697.14 cm³
Whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops.
Let the radius of hemisphere and base of cone be r’
Height of cone = h = 4 times the radius of its base
h’ = 4r’
Volume of Hemisphere = 2/3 π(r’)³
Volume of cone = 1/3 π(r’)²h’ = 1/3 π(r’)² × 4r’
= 2/3 π(r’)³
Volume of ice-cream = Volume of Hemisphere + Volume of cone
= 2/3 π(r’)³ + 4/3 π(r’)³ = 6/3 π(r’)³
Number of ice-creams = 10
∴ total volume of ice-cream = 10 × Volume of ice-cream
= 10 × 6/3 π(r’)³ = 60/3 π(r’)³
Also, total volume of ice-cream = Volume of cylindrical container
⇒ 60/3 π(r’)³ = 1697.14 cm³
⇒ 60/3 × 22/7 × (r’)³ = 1697.14 cm³
⇒ (r’)³ = 1697.14 × 3/60 × 7/22 = 27 cm³
⇒ r = 3 cm
∴ Radius of ice-cream cone = 3 cm

Q.17. A vessel is in the form of a hemispherical bowl surmounted by a hallow cylinder. The diameter of the hemisphere is 21 cm and the total height of the vessel is 14.5 cm. Find its capacity.

Vessel is in the form of a hemispherical bowl surmounted by a hallow cylinder.
Diameter of hemisphere = 21 cm
Radius of hemisphere = 10.5 cm
Volume of hemisphere = 2/3 πr³ = 2/3 × 22/7 × 10.5³ cm³
= 2425.5 cm³
Total height of vessel = 14.5 cm
Height of cylinder = h = Total height of vessel - Radius of hemisphere
= 14.5 – 10.5 cm = 4 cm
Volume of cylinder = πr²h = 22/7 × 10.5 × 10.5 × 4 cm³
= 1386 cm³
Volume of vessel = Volume of hemisphere + Volume of cylinder
= 2425.5 cm³ + 1386 cm³
= 3811.5 cm³
∴ Capacity of vessel = 3811.5 cm³

Q.18. A toy is in the form of a cylinder with hemisphere ends. If the whole length of the toy is 90 cm and its diameter is 42 cm, find the cost of painting the toy at the rate of 70paise per sq cm.

Toy is in the form of a cylinder with hemisphere ends
Total length of toy = 90 cm
Diameter of toy = 42 cm
Radius of toy = r = 21 cm
Length of cylinder = l = Total length of toy – 2 × Radius of toy
= 90 – 2 × 21 cm = 48 cm
For cost of painting we need to find out the curved surface area of toy
Curved surface area of cylinder = 2πrl
= 2 × 22/7 × 21 × 48 cm²
= 6336 cm²
Curved surface area of hemispherical ends = 2 × 2πr²
= 2 × 2 × 22/7 × 21 × 21 cm²
= 5544 cm²
Surface area of toy = Curved surface area of cylinder + Curved surface area of hemispherical ends
Surface area of toy = 6336 cm² + 5544 cm² = 11880 cm²
Cost of painting = Rs 0.70/cm²
Total Cost of painting = Surface area of toy × Cost of painting
= 11880 cm² × Rs 0.70/cm² = Rs 8316.00
Total cost of painting the toy = Rs 8316.00

Q.19. A medicine capsule is in the shape of a cylinder with two hemisphere stuck to each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

A medicine capsule is in the shape of a cylinder with two hemisphere stuck to each of its ends.
Total length of entire capsule = 14 mm
Diameter of capsule = 5 mm
Radius of capsule = r = Diameter ÷ 2 = 5/2 mm = 2.5 mm
Length of cylindrical part of capsule = l = Total length of entire capsule – 2 × Radius of capsule
= 14 – 2 × 2.5 mm = 14 - 5 mm = 9 mm
Curved surface area of cylindrical part of capsule = 2πrl
= 2 × 3.14 × 9 × 2.5 mm²
= 141.3 mm²
Curved surface area of hemispherical ends = 2 × 2πr²
= 2 × 2 × 3.14 × 2.5 × 2.5 cm²
= 78.5 mm²
Surface area of capsule = Curved surface area of cylindrical part of capsule + Curved surface area of hemispherical ends
Surface area of capsule = 141.3 mm² + 78.5 mm² = 219.8 mm².

Q.20. A wooden article was made by scooting out a hemisphere from each end of a cylinder, as shown in the figure. If the height of the cylinder is 20 cm and its base is of diameter 7 cm, find the total surface area of the article when it is ready.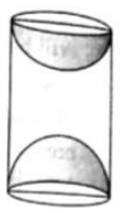

The wooden article was made by scooting out a hemisphere from each end of a cylinder
Let the radius of cylinder be r cm and height be h cm.
Height of cylinder = h = 20 cm
Base diameter of cylinder = 7 cm
Base radius of cylinder = r = diameter ÷ 2 = 7/2 cm = 3.5 cm
Lateral Surface area of cylinder = 2πrh
= 2 × 22/7 × 3.5 × 20 cm²
= 2 × 22/7 × 3.5 × 20 cm²
= 440 cm²
Since, the wooden article was made by scooting out a hemisphere from each end of a cylinder
∴ Two hemispheres are taken out in total
Radius of cylinder = radius of hemisphere
∴ Radius of hemisphere = 3.5 cm
Lateral Surface area of hemisphere = 2πr²
= 2 × 22/7 × 3.5 × 3.5 cm²
= 77 cm²
Total Surface area of two hemispheres = 2 × 77 cm² = 154 cm²
Total surface area of the article when it is ready = Lateral Surface area of cylinder + Lateral Surface area of hemisphere
Total surface area of the article when it is ready = 440 cm² + 154 cm²
= 594 cm²

Q.21. A solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is 2.1 cm and the height of the cone is 4 cm. The solid is placed in a cylindrical tub full of water in such a way that the whole solid is submerged in water. If the radius of the cylinder is 5 cm and its height is 9.8 cm, find the volume of the water left in the tub.

A solid is in the form of a right circular cone mounted on a hemisphere.
Let r be the radius of hemisphere and cone
Let h be the height of the cone
Radius of hemisphere = r = 2.1 cm
Volume of hemisphere = 2/3 πr³
= 2/3 × 22/7 × 2.1 × 2.1 × 2.1 cm³
= 19.404 cm³
Height of cone = h = 4 cm
Radius of cone = r = 2.1 cm
Volume of cone = 1/3 πr²h
= 1/3 × 22/7 × 2.1 × 2.1 × 4 cm³
= 18.48 cm³
Volume of solid = Volume of hemisphere + Volume of cone
= 19.404 cm³ + 18.48 cm³ = 37.884 cm³
The solid is placed in a cylindrical tub full of water in such a way that the whole solid is submerged in water, so, to find the volume of water left in the tub we need to subtract volume of solid from cylindrical tub.
Radius of cylinder = r’ = 5 cm
Height of cylinder = h’ = 9.8 cm
Volume of cylindrical tub = πr’²h’ = 22/7 × 5 × 5 × 9.8 cm³
= 770 cm³
Volume of water left in the tub = Volume of cylindrical tub – Volume of solid
Volume of water left in the tub = 770 cm³ – 37.884 cm³ = 732.116 cm³
∴ Volume of water left in the tub is 732.116 cm³.

Q.22. From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume of the remaining solid. Also, find the total surface area of the remaining solid. [Take π = 3.14.]

Height of solid cylinder = h = 8 cm
Radius of solid cylinder = r = 6 cm
Volume of solid cylinder = πr²h
= 3.14 × 6 × 6 × 8 cm³
= 904.32 cm³
Curved Surface area of solid cylinder = 2πrh
Height of conical cavity = h = 8 cm
Radius conical cavity = r = 6 cm
Volume of conical cavity = 1/3 πr²h
= 1/3 × 3.14 × 6 × 6 × 8 cm³
= 301.44 cm³
Let l be the slant height of conical cavity
l² = r² + h²
⇒ l² = (6² + 8²) cm²
⇒ l² = (36 + 64) cm²
⇒ l² = 100 cm²
⇒ l = 10 cm
Curved Surface area of conical cavity = πrl
Since, conical cavity is hollowed out from solid cylinder, so, volume and total surface area of remaining solid will be found out by subtracting volume and total surface area of conical cavity from volume and total surface area of solid cylinder.
Volume of remaining solid = Volume of solid cylinder – Volume of conical cavity
Volume of remaining solid = 904.32 cm³ – 301.44 cm³
= 602.88 cm³
Total surface area of remaining solid = Curved Surface area of solid cylinder + Curved Surface area of conical cavity + Area of circular base
Total surface area of remaining solid = 2πrh + πrl + πr²
= πr × (2h + l + r)
= 3.14 × 6 × (2 × 8 + 10 + 6) cm²
= 3.14 × 6 × 32 cm²
= 602.88 cm²

Q.23. From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.

Height of solid cylinder = h = 2.8 cm
Diameter of solid cylinder = 4.2 cm
Radius of solid cylinder = r = Diameter ÷ 2 = 2.1 cm
Curved Surface area of solid cylinder = 2πrh
= 2 × 22/7 × 2.1 × 2.8 cm²
= 2 × 22/7 × 2.1 × 2.8 cm²
= 36.96 cm²
Height of conical cavity = h = 2.8 cm
Radius conical cavity = r = 2.1 cm
Let l be the slant height of conical cavity
l² = r² + h²
⇒ l² = (2.8² + 2.1²) cm²
⇒ l² = (7.84 + 4.41) cm²
⇒ l² = 12.25 cm²
⇒ l = 3.5 cm
Curved Surface area of conical cavity = πrl
= 22/7 × 2.1 × 3.5
= 23.1 cm²
Total surface area of remaining solid = Curved surface area of solid cylinder + Curved surface area of conical cavity + Area of circular base
Total surface area of remaining solid = (36.96 + 23.1 + 22/7 × 2.1²) cm²
= (36.96 + 23.1 + 13.86) cm²
= 73.92 cm²

Q.24. From a solid cylinder of height 14 cm and base diameter 7 cm, two equal conical holes each of radius 2.1 cm and height 4 cm are cut off. Find the volume of the remaining solid.

Height of solid cylinder = h = 14 cm
Diameter of solid cylinder = 7 cm
Radius of solid cylinder = r = Diameter ÷ 2 = 7/2 cm = 3.5 cm
Volume of solid cylinder = πr²h
= 22/7 × 3.5 × 3.5 × 14 cm³
= 539 cm³
Height of conical cavity = h’ = 4 cm
Radius conical cavity = r’ = 2.1 cm
Volume of conical cavity = 1/3 πr’²h’
= 1/3 × 22/7 × 2.1 × 2.1 × 4 cm³
= 18.48 cm³
Since, there are two conical cavities
∴ Volume of two conical cavities = 2 × 18.48 cm³ = 36.96 cm³
Volume of remaining solid = Volume of solid cylinder – Volume of two conical cavity
Volume of remaining solid = 539 cm³ – 36.96 cm³
= 502.04 cm³

Q.25. A metallic cylinder has radius 3 cm and height 5 cm. To redue its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of 3/2 cm and its depth is 8/9 cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.

Height of metallic cylinder = h = 5 cm
Radius of metallic cylinder = r = 3 cm
Volume of solid cylinder = πr²h
= π × 3 × 3 × 5 cm³
= 45π cm³
Height of conical hole = h’ = 8/9 cm
Radius conical hole = r’ = 3/2 cm
Volume of conical hole = 1/3 πr’²h’
= 1/3 × π × 3/2 × 3/2 × 8/9 cm³
= 2/3 π cm³
Volume of metal left in cylinder = Volume of metallic cylinder – Volume of conical hole
Volume of metal left in cylinder = 45π - 2/3 π = 133π/3
Ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape = Volume of metal left in cylinder/ Volume of conical hole
Volume of metal left in cylinder : Volume of conical hole = 133π/3 : 2/3 π
Volume of metal left in cylinder: Volume of conical hole = 133: 2
Ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape is 339:4.

Q.26. A spherical glass vessel has a cylindrical neck 7 cm long and 4 cm in diameter. The diameter of the spherical part is 21cm. Find the quantity of water it can hold. [Use π = 22/7]

Length of cylindrical neck = l = 7 cm
Diameter of cylindrical neck = 4 cm
Radius of cylindrical neck = r = Diameter ÷ 2 = 4/2 cm = 2 cm
Volume of cylindrical neck = πr²l
= 22/7 × 2 × 2 × 7 cm³
= 88 cm³
Diameter of spherical part = 21 cm
Radius of spherical part = r’ = Diameter ÷ 2 = 21/2 cm = 10.5 cm
Volume of spherical part = 4/3 πr’³
= 4/3 × 22/7 × 10.5 × 10.5 × 10.5 cm³
= 4851 cm³
Quantity of water spherical glass vessel with cylindrical neck can hold = Volume of spherical part + Volume of cylindrical neck
Quantity of water spherical glass vessel with cylindrical neck can hold = 4851 cm³ + 88 cm³ = 4939 cm³
Quantity of water spherical glass vessel with cylindrical neck can hold is 4939 cm³.

Q.27. The given figure represent a solid consisting of a cylinder surmounted by a cone at one end a hemisphere at the other. Find the volume of the solid.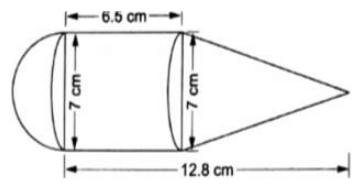

The solid consisting of a cylinder surmounted by a cone at one end a hemisphere at the other.
Length of cylinder = l = 6.5 cm
Diameter of cylinder = 7 cm
Radius of cylinder = r = Diameter ÷ 2 = 7/2 cm = 3.5 cm
Volume of cylinder = πr²l
= 22/7 × 3.5 × 3.5 × 6.5 cm³
= 250.25 cm³
Length of cone = l’ = 12.8 cm – 6.5 cm = 6.3 cm
Diameter of cone = 7 cm
Radius of cone = r = Diameter ÷ 2 = 7/2 cm = 3.5 cm
Volume of cone = 1/3 πr²l’
= 1/3 × 22/7 × 3.5 × 3.5 × 6.3 cm³
= 80.85 cm³
Diameter of hemisphere = 7 cm
Radius of hemisphere = r = Diameter ÷ 2 = 7/2 cm = 3.5 cm
Volume of hemisphere = 2/3 πr³
= 2/3 × 22/7 × 3.5 × 3.5 × 3.5 cm³
= 89.83 cm³
Volume of the solid = Volume of cylinder + Volume of cone + Volume of hemisphere
Volume of solid = 250.25 cm³ + 80.85 cm³ + 89.83 cm³
= 420.93 cm³

Q.28. From a cubical piece of wood of side 21 cm, a hemisphere is carved out in such a way that the diameter of the hemisphere is equal to the side of the cubical piece. Find the surface area and volume of the remaining piece.

Length of cubical piece of wood = a = 21 cm
Volume of cubical piece of wood = a³
= 21 × 21 × 21 cm³
= 9261 cm³
Surface area of cubical piece of wood = 6a²
= 6 × 21 × 21 cm²
= 2646 cm²
Since, a hemisphere is carved out in such a way that the diameter of the hemisphere is equal to the side of the cubical piece.
So, diameter of hemisphere = length of side of the cubical piece
Diameter of hemisphere = 21 cm
Radius of hemisphere = r = Diameter ÷ 2 = 21/2 cm = 10.5 cm
Volume of hemisphere = 2/3 πr³
= 2/3 × 22/7 × 10.5 × 10.5 × 10.5 cm³
= 2425.5 cm³
Surface area of hemisphere = 2πr²
= 2 × 22/7 × 10.5 × 10.5 cm²
= 693 cm²
A hemisphere is carved out from cubical piece of wood
Volume of remaining solid = Volume of cubical piece of wood – Volume of hemisphere
Volume of remaining solid = 9261cm³ – 2425.5 cm³ = 6835.5 cm³
Surface area remaining piece of solid = surface area of cubical piece of wood – Area of circular base of hemisphere + Curved Surface area of hemisphere
Surface area remaining piece of solid = 6a² – πr² + 2πr²
= (2646 – 22/7 × 10.5² + 693) cm²
= 2992.5 cm²

Q.29. A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs 5 per 100 sq cm. [Use π = 3.14.]

Length of side of cubical block = a = 10 cm
Since, a cubical block is surmounted by a hemisphere, so, the largest diameter of hemisphere = 10 cm
Since, hemisphere will be touching the sides of cubical block.
Radius of hemisphere = r = Diameter ÷ 2 = 10/2 cm = 5 cm
Surface area of solid = Surface area of cube – Area of circular part of hemisphere + Curved surface area of hemisphere
Total Surface area of solid = 6a² – πr² + 2πr² = 6a² + πr²
= 6 × 10 × 10 cm² + 3.14 × 5 × 5 cm²
= 678.5 cm²
Rate of painting = Rs 5/100 cm²
Cost of painting the total surface area of the solid so formed = Total Surface area of solid × Rate of painting
Cost of painting the total surface area of the solid = Rs 5/100 × 678.5
= Rs 33.925

Q.30. A toy is in the shape of a right circular cylinder with a hemisphere on one end a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively. The radii of the hemispherical and the conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.

The toy is in the shape of a right circular cylinder surmounted by a cone at one end a hemisphere at the other.
Total height of toy = 30 cm
Height of cylinder = h = 13 cm
Radius of cylinder = r = 5 cm
Curved surface area of cylinder = 2πrh
= 2 × 22/7 × 5 × 13 cm²
Height of cone = h’ = Total height of toy – Height of cylinder – Radius of hemisphere
Height of cone = h’ = 30 cm – 13 cm – 5 cm = 12 cm
Radius of cone = r = Radius of cylinder
Radius of cone = r = 5 cm
Let the slant height of cone be l
l² = h’² + r²
⇒ l² = 12² + 5² cm² = 144 + 25 cm² = 169 cm²
⇒ l = 13 cm
Curved surface area of cone = πrl
= 22/7 × 5 × 13 cm²
Radius of hemisphere = r = Radius of cylinder
Radius of hemisphere = r = 5 cm
Curved surface area of hemisphere = 2πr²
= 2 × 22/7 × 5 × 5 cm²
Surface area of the toy = Surface area of cylinder + Surface area of cone + Surface area of hemisphere
Surface area of toy = 2πrh + πrl + 2πr²
= πr (2h + l + 2r)
= 22/7 × 5 × (2 × 13 + 13 + 2 × 5) cm²
= 22/7 × 5 × 49 cm²
= 770 cm²
Surface area of toy is 770 cm².

Q.31. The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.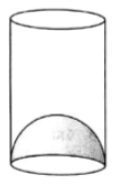

Inner diameter of a glass = 7 cm
Inner radius of glass = r = 7/2 cm = 3.5 cm
Height of glass = h = 16 cm
Apparent capacity of glass = πr²h
= 22/7 × 3.5 × 3.5 × 16 cm³
= 616 cm³
Volume of the hemisphere in the bottom = 2/3 πr³
= 2/3 × 22/7 × 3.5³ cm³
= 89.83 cm³
Actual capacity of the class = Apparent capacity of glass – Volume of the hemisphere
Actual capacity of the class = 616 cm³ – 89.83 cm³ = 526.17 cm³.

Q.32. A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part in 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of them colours. [Take π = 22/7.]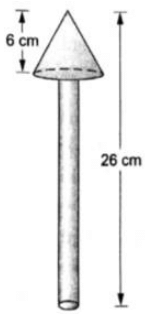

The wooden toy is in the shape of a cone mounted on a cylinder
Total height of the toy = 26 cm
Height of conical part = H = 6 cm
Height of cylindrical part = Total height of the toy – Height of conical part
h = 26 cm – 6 cm = 20 cm
Diameter of conical part = 5 cm
Radius of conical part = R = Diameter/2 = 5/2 cm = 2.5 cm
Let L be the slant height of the cone
L² = H² + R²
⇒ L² = 62 + 2.52 cm² = 36 + 6.25 cm² = 42.25 cm²
⇒ L = 6.5 cm
Diameter of cylindrical part = 4 cm
Radius of cylindrical part = r = Diameter/2 = 4/2 cm = 2 cm
Area to be painted Red = Curved Surface area of cone + Base area of cone – base area of cylinder
Area to be painted Red = πRL + πR² – πr² = π (RL + R² – r²)
= 22/7 × (2.5 × 6.5 + 2.5 × 2.5 – 2 × 2) cm²
= 22/7 × (16.25 + 6.25 – 4) cm²
= 22/7 × 18.5 cm²
= 58.143 cm²
Area to be painted White = Curved Surface area of cylinder + Base area of cylinder
Area to be painted White = 2πrh + πr² = πr (2h + r)
= 22/7 × 2 × (2 × 20 + 2) cm²
= 22/7 × 2 × (40 + 2) cm²
= 22/7 × 2 × 42 cm² = 264 cm²
∴ Area to be painted red is 58.143 cm² and area to be painted white is 264 cm².