Relative Stability Analysis | Control Systems - Electrical Engineering (EE) PDF Download

Routh-Hurwitz Stability Criterion

• Routh-Hurwitz stability criterion is having one necessary condition and one sufficient condition for stability. If any control system doesn’t satisfy the necessary condition, then we can say that the control system is unstable. But, if the control system satisfies the necessary condition, then it may or may not be stable. So, the sufficient condition is helpful for knowing whether the control system is stable or not.

Necessary Condition for Routh-Hurwitz Stability

• The necessary condition is that the coefficients of the characteristic polynomial should be positive. This implies that all the roots of the characteristic equation should have negative real parts.
• Consider the characteristic equation of the order ‘n’ is -
  
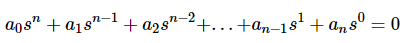
• Note that, there should not be any term missing in the nth order characteristic equation. This means that the nth order characteristic equation should not have any coefficient that is of zero value.

Sufficient Condition for Routh-Hurwitz Stability

• The sufficient condition is that all the elements of the first column of the Routh array should have the same sign. This means that all the elements of the first column of the Routh array should be either positive or negative.

Routh Array Method

• If all the roots of the characteristic equation exist to the left half of the ‘s’ plane, then the control system is stable. If at least one root of the characteristic equation exists to the right half of the ‘s’ plane, then the control system is unstable. So, we have to find the roots of the characteristic equation to know whether the control system is stable or unstable. But, it is difficult to find the roots of the characteristic equation as order increases.
• So, to overcome this problem there we have the Routh array method. In this method, there is no need to calculate the roots of the characteristic equation. First formulate the Routh table and find the number of the sign changes in the first column of the Routh table. The number of sign changes in the first column of the Routh table gives the number of roots of characteristic equation that exist in the right half of the ‘s’ plane and the control system is unstable.

Follow this procedure for forming the Routh table.

• Fill the first two rows of the Routh array with the coefficients of the characteristic polynomial as mentioned in the table below. Start with the coefficient of sn and continue up to the coefficient of s0.
• Fill the remaining rows of the Routh array with the elements as mentioned in the table below. Continue this process till you get the first column element of row s0 is an. Here, an is the coefficient of s0 in the characteristic polynomial.

Note − If any row elements of the Routh table have some common factor, then you can divide the row elements with that factor for the simplification will be easy.
The following table shows the Routh array of the nth order characteristic polynomial.

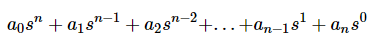
Example: Let us find the stability of the control system having characteristic equation,
s⁴ + 3s³ + 3s² + 2s + 1 = 0
Step 1 − Verify the necessary condition for the Routh-Hurwitz stability.
All the coefficients of the characteristic polynomial, s⁴ + 3s³ + 3s² + 2s + 1 are positive. So, the control system satisfies the necessary condition.
Step 2 − Form the Routh array for the given characteristic polynomial.

Step 3 − Verify the sufficient condition for the Routh-Hurwitz stability.
All the elements of the first column of the Routh array are positive. There is no sign change in the first column of the Routh array. So, the control system is stable.

Special Cases of Routh Array

We may come across two types of situations, while forming the Routh table. It is difficult to complete the Routh table from these two situations.
The two special cases are −

• The first element of any row of the Routh array is zero.
• All the elements of any row of the Routh array are zero.

Let us now discuss how to overcome the difficulty in these two cases, one by one.

First Element of any row of the Routh array is zero

• If any row of the Routh array contains only the first element as zero and at least one of the remaining elements have non-zero value, then replace the first element with a small positive integer, ϵ. And then continue the process of completing the Routh table. Now, find the number of sign changes in the first column of the Routh table by substituting ϵ tends to zero.

Example:  Let us find the stability of the control system having characteristic equation,
s⁴ + 2s³ + s² + 2s + 1 = 0

Step 1 − Verify the necessary condition for the Routh-Hurwitz stability.
All the coefficients of the characteristic polynomial, s⁴ + 2s³ + s² + 2s + 1 are positive. So, the control system satisfied the necessary condition.
Step 2 − Form the Routh array for the given characteristic polynomial.

The row s³ elements have 2 as the common factor. So, all these elements are divided by 2.
Special case (i) − Only the first element of row s² is zero. So, replace it by ϵ and continue the process of completing the Routh table.

Step 3 − Verify the sufficient condition for the Routh-Hurwitz stability.
As ϵ tends to zero, the Routh table becomes like this.

There are two sign changes in the first column of Routh table. Hence, the control system is unstable.

All the Elements of any row of the Routh array are zero
In this case, follow these two steps −

• Write the auxilary equation, A(s) of the row, which is just above the row of zeros.
• Differentiate the auxiliary equation, A(s) with respect to s. Fill the row of zeros with these coefficients.

Example: Let us find the stability of the control system having characteristic equation,
s⁵ + 3s⁴ + s³ + 3s² + s + 3 = 0

Step 1 − Verify the necessary condition for the Routh-Hurwitz stability.
All the coefficients of the given characteristic polynomial are positive. So, the control system satisfied the necessary condition.
Step 2 − Form the Routh array for the given characteristic polynomial.

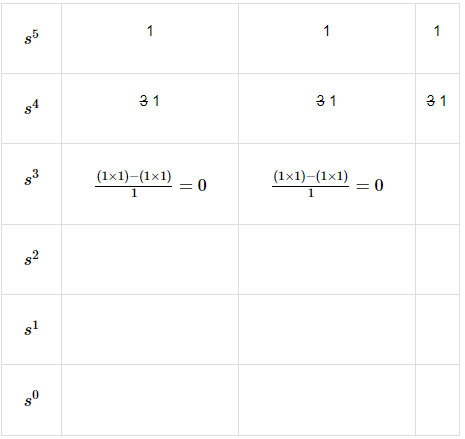The row s⁴ elements have the common factor of 3. So, all these elements are divided by 3.
Special case (ii) − All the elements of row s³ are zero. So, write the auxiliary equation, A(s) of the row s⁴.
A(s) = s⁴ + s² + 1

Differentiate the above equation with respect to s.
dA(s)/ds = 4s³ + 2s
Place these coefficients in row s³.

Step 3 − Verify the sufficient condition for the Routh-Hurwitz stability.
There are two sign changes in the first column of Routh table. Hence, the control system is unstable.