Resistance of a System of Resistors | Science Class 10 PDF Download
| Table of contents |

|
| What is a Resistor? |

|
| Resistors in Series |

|
| Resistors in Parallel |

|
| Devices in Series and Parallel |

|
What is a Resistor?
A passive electrical component with two terminals that are used for either limiting or regulating the flow of electric current in electrical circuits.
- A conducting material (e.g., a wire) of a particular resistance meant for use in a circuit is called a resistor.
- A resistor is sometimes simply referred to as resistance. It is represented by the symbol.
- Two or more resistors can be connected in series, in parallel or in a manner that is a combination of these two.
 Resistor
Resistor
Resistors in Series
Two or more resistors are said to be connected in series if the current flowing through one also flows through the rest.
The total potential difference across the combination of resistors connected in series is equal to the sum of the potential differences across the individual resistors.
V = V1 + V2 + V3
 Resistors in Series
Resistors in Series
Equivalent Resistance in Series Connection
Figure (a) shows three resistors of resistances R1, R2 and R3 connected in series. The cell connected across the combination maintains a potential difference V across the combination. The current through the cell is i. The same current i flows through each resistor.
Let us replace the combination of resistors with a single resistor Req such that the current does not change, i.e., it remains i. This resistance is called the equivalent resistance of the combination, and its value is given by Ohm's law as Req = V / i
Thus V = i Req.

The potential differences V1 , V2 and V3 across the resistors R1 , R2 and R3 respectively are given by
Ohm's law as : V1 = iR1 , V2 = iR2 , V3 = iR3
Since the resistors are in series, V = V1 + V2 + V3
Substituting the values of the potential differences in the above equation,
iReq = iR1 + iR2 + iR3
or iReq = i(R1 +R2 +R3)
or Req = R1 + R2 + R3
Similarly, for n resistors connected in series,
Equivalent resistance of resistors in series : Req = R1 + R2 + R3 + .... Rn
Resistors in Parallel
The total current flowing into the combination is equal to the sum of the currents passing through the individual resistors.
i = i1 + i2 + i3
If resistors are connected in such a way that the same potential difference gets applied to each of them, they are said to be connected in parallel.
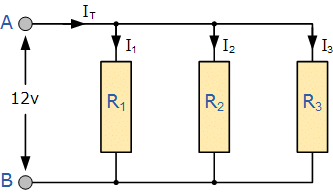 Resistors in Parallel
Resistors in Parallel
Equivalent Resistance in Parallel Connection
Figure (a) shows three resistors of resistances R1, R2 and R3 connected in parallel across points A and B. The cell connected across these two points maintains a potential difference V across each resistor. The current through the cell is i. It gets divided at A into three parts i1, i2 and i3, which flow through R1, R2 and R3 respectively.

Let us replace the combination of resistors with an equivalent resistor Req such that the current i in the circuit does not change (Fig). The equivalent resistance is given by Ohm's law as Req = V/i.
Thus,

The currents i1 , i2 and i3 through the resistors R1, R2 and R3 respectively are given by Ohm's law as

Since the resistors are in parallel,
i = i1 + i2 + i3
Substituting the values of the currents in the above equation,

Similarly, if there are n resistors connected in parallel, their equivalent resistance Req is given by
Equivalent resistance of resistors in parallel:

For two resistances R1 and R2 connected in parallel,

The equivalent resistance in a parallel connection is less than each of the resistances.
When a resistance is joined parallel to a comparatively smaller resistance, the equivalent resistance is very close to the value of the smaller resistance.
Note: If a resistor connected in series with others is removed or fails, the current through each resistor becomes zero. On the other hand, if a resistor connected in parallel with others fails or is removed, the current continues to flow through the other resistors.
 |
Download the notes
Resistance of a System of Resistors
|
Download as PDF |
Distribution of Current in Two Resistors in Parallel
Consider the circuit in Fig. The resistors R1 and R2 are connected in parallel. The current i gets distributed in the two resistors.
i = i1 + i2 .....(i)
Applying Ohm's law to the resistor R1
VA - VB =R1i1· .....(ii)
And applying Ohm's law to the resistor R2
VA - VB = R2i2 .... (iii)
From (ii) and (iii), R1i1 = R2i2 or 
Substituting for i2 in (i), we have
or 
Similarly, 
Thus, 
The current through each branch in a parallel combination of resistors is inversely proportional to its resistance.
Devices in Series and Parallel
You must have seen tiny bulbs strung together for decorating buildings during festivals like Diwali, and occasions like marriages, etc.
- These bulbs are connected in series, and the mains voltage is applied to the combination. The potential difference (V) of the mains gets divided across the bulbs (V = V1 + V2 + V3 + ... ).
- So, a small potential difference exists across each bulb, close to that required to make the bulb work. However, the same current flows through all the bulbs. So, if one bulb goes bad, the current through it stops, and this stops the current through the rest of the bulbs as well.
- To make the chain of lights work, we have to find and replace the defective bulb. This problem does not occur with the lights in our house. That is because in houses, lights, fans, etc., are connected in parallel.
- In a parallel connection, the same mains voltage gets applied to each device, but the current through each is different. If one of them goes bad, the current in the other branches of the parallel connection does not stop.
- Another advantage of parallel connection is that, unlike series connection, each device can draw a different current, as per its requirement.
|
80 videos|512 docs|74 tests
|























