Revision Notes: Binomial Theorem & its Simple Applications | Mathematics (Maths) for JEE Main & Advanced PDF Download
Revision Notes On Binomial Theorem
If x, y ∈ R and n ∈ N, then the binomial theorem states that (x+y)n = nC0xn + nC1 xn-1y+ nC2 xn-2 y2 +…… … .. + nCrxn-r yr + ….. + nCnyn which can be written as ΣnCrxn-ryr. This is also called as the binomial theorem formula which is used for solving many problems.
- Some chief properties of binomial expansion of the term (x+y)n:
- The number of terms in the expansion is (n+1) i.e. it is one more than the index.
- The sum of indices of x and y is always n.
- The binomial coefficients of the terms which are equidistant from the starting and the end are always equal. The simple reason behind this is C(n, r) = C(n, n-r) which gives C(n, n) C(n, 1) = C(n, n-1) C(n, 2) = C(n, n-2).
- Such an expansion always follows a simple rule which is:
- The subscript of C i.e. the lower suffix of C is always equal to the index of y.
- Index of x = n – (lower suffix of C).
The (r +1)thterm in the expansion of expression (x+y)n is called the general term and is given by Tr+1 = nCrxn-ryr
The term independent of x is obviously without x and is that value of r for which the exponent of x is zero.
The middle term of the binomial coefficient depends on thevalue of n. There can be two different cases according to whether n is even or n is odd.
- If n is even, then the total number of terms are odd and in that case there is a single middle term which is (n/2 +1)th and is given by nCn/2 an/2 xn/2.
- On the other hand, if n is odd, the total number of terms is even and then there are two middle terms [(n+1)/2]thand [(n+3)/2]th which are equal to nC(n-1)/2 a(n+1)/2 x(n-1)/2 and nC(n+1)/2 a(n-1)/2 x(n+1)/2
The binomial coefficient of the middle term is the greatest binomial coefficient of the expansion.
Some of the standard binomial theorem formulas which should be memorized are listed below:
- C0 + C1 + C2 + ….. + Cn= 2n
- C0 + C2 + C4 + ….. = C1 + C3 + C5 + ……….= 2n-1
- C02 + C12 + C22 + ….. + Cn2 = 2nCn = (2n!)/ n!n!
- C0Cr + C1Cr+1 + C2Cr+2+ ….. + Cn-rCn=(2n!)/ (n+r)!(n-r)!
- Another result that is applied in binomial theorem problems is nCr + nCr-1 = n+1Cr
- We can also replace mC0 by m+1C0 because numerical value of both is same i.e. 1. Similarly we can replace mCm by m+1Cm+1.
- Note that (2n!) = 2n. n! [1.3.5. … (2n-1)]
In order to compute numerically greatest term in a binomial expansion of (1+x)n, find Tr+1 / Tr= (n – r + 1)x/r. Then put the absolute value of x and find the value of r which is consistent with the inequality Tr+1 / Tr> 1.
If the index n is other than a positive integer such as a negative integer or fraction, then the number of terms in the expansion of (1+x)nis infinite.
The expansions in ascending powers of x are valid only if x is small. If x is large, i.e. |x| > 1 then it is convenient to expand in powers of 1/x which is then small.
The binomial expansion for the nth degree polynomial is given by:
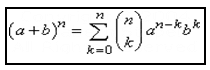
Following expansions should be remembered for |x| < 1:
- (1+x)-1 = 1 – x + x2 – x3 + x4 - ….. ∞
- (1-x)-1 = 1 + x + x2+ x3 + x4+ ….. ∞
- (1+x)-2 = 1 – 2x + 3x2 – 4x3 + 5x4 - ….. ∞
- (1-x)-2 = 1 +2x + 3x2+4x3 + 5x4+ ….. ∞
|
172 videos|503 docs|154 tests
|





















