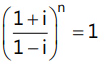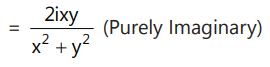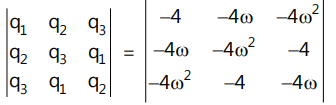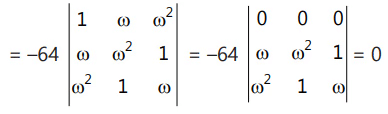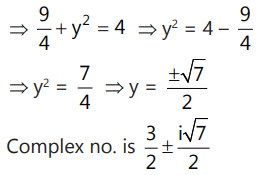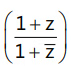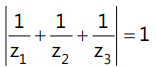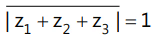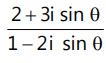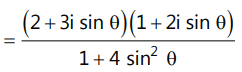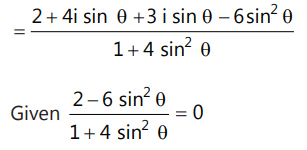Revision Notes: Complex Numbers | Mathematics (Maths) for JEE Main & Advanced PDF Download
Important Formulas
(a) Complex numberz = x + iy, where x, y ∈ R and i = √-l.
(b) If z = x + iy then its conjugate z = x - iy.
(c) Modulus of z, i.e. | z | = 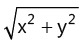 (d) Argument of z, i.e.
(d) Argument of z, i.e.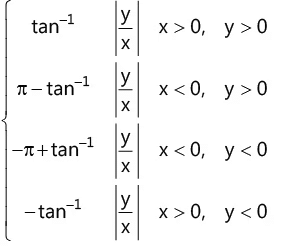
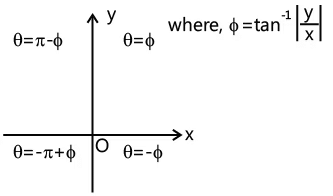
(e) If y=0, then argument of z, i.e.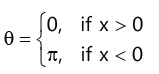 (f) If x=0, then argument of z, i.e.
(f) If x=0, then argument of z, i.e.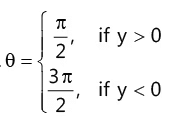
(g) In Polar form x = rcosθ and y = rsinθ , therefore z = r ( cosθ+ i sinθ )
(h) In exponential form complex number z = reiθ , where eiθ = cosθ+ isinθ .
(i)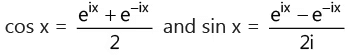
( j) Important properties of conjugate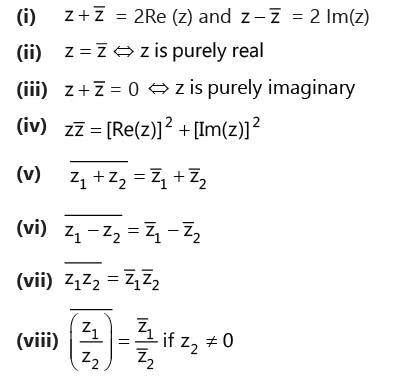
(k) Important properties of modulus
If z is a complex number, then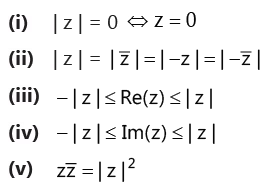 If z1 ,z2 are two complex numbers, then
If z1 ,z2 are two complex numbers, then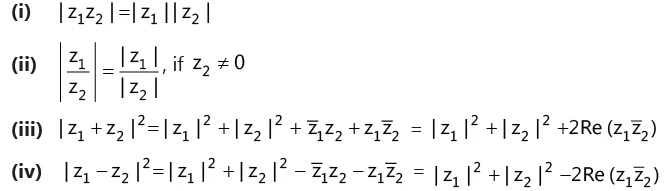
(l) Important properties of argument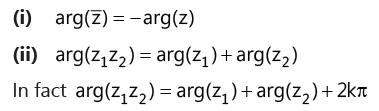
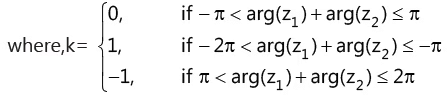
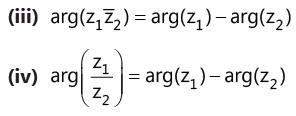
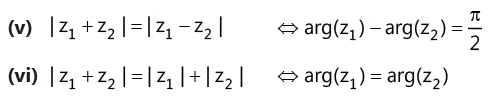
If z1 = r1 (cos θ1+ i sin θ1 ) and z2 = r2 (cos θ2 + i sin θ2 ) , then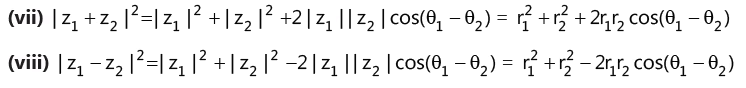
(m) Triangle on the complex plane
(n) ( cos θ+ i sin θ )n = cos nθ+ i sin nθ
(o) 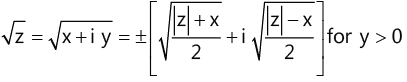 (p) Distance between A (z1 ) and B(z2 ) is given by |z2 − z1 |
(p) Distance between A (z1 ) and B(z2 ) is given by |z2 − z1 |
(q) Section formula: The point P (z) which divides the join of the segment AB in the ratio m : n
is given by z = 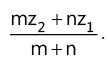
(r) Midpoint formula: 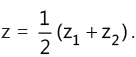
(s) Equation of a straight line
(i) Non-parametric form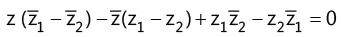 (ii) Parametric form
(ii) Parametric form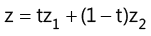 (iii) General equation of straight line
(iii) General equation of straight line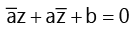
(t) Complex slope of a line, 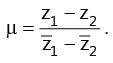 Two lines with complex slopes µ1 and µ2 are
Two lines with complex slopes µ1 and µ2 are
(i) Parallel, if µ1= µ2
(ii) Perpendicular, if µ1 +µ2 = 0
(u) Equation of a circle: |z − z0 |= r
Solved Examples
Que 1: Find the value of smallest positive integer n, for which
Ans:
⇒in = 1 ⇒ n = 4, 8, 12
Minimum value of n is 4
Que 2: If z = 1 + i tan α (1, where π < α < 3π/2. find the value of |z| cos α.
Ans: z = 1 + itan α
sec α < 0 ⇒ |secα| = –sec α|z| = –secα|z|cosα = –1
Que 3: Find the common roots of the equation z3 + 2z2 + 2z + 1 = 0 and z1985 + z100 + 1 = 0.
Ans: z3 + 2z2 + 2z + 1 = 0
⇒ z = –1, ω, ω2
z1985 + z100 + 1 = 0
⇒ z = ω, ω2
Common roots are ω, ω2
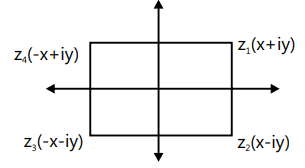
Que 4: If z1 , z2 , z3 , z4 are the vertices of a square in that order, then which of the following does not hold good?
(a)
(b)
(c) (d) None of these
(d) None of these
Ans: (c)
z1, z2, z3, z4 vertices of square
z1 – z2 = i2Im(z1)
z3 – z2 = –2Re(z1)z2 – z4 = [–x + iy – (x – iy)]
= 2Re(z) – i2lm(z)
z1 – z3 = 2x + 2iy = 2Re(z) + i2Im(z)(x = y as it is aqueous)
Que 5: If q1 , q2 , q3 are the roots of the equation, x3 + 64 = 0, then the value of the determinant 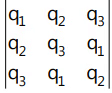 is:(a) 1
is:(a) 1
(b) 4
(c) 10
(d) none of these
Ans: (d)
x3 = (4)3 (–1)1/3
x -4, -4ω, -4ω2
Que 6: The points of intersection of the two curves |z – 3| = 2 and |z| = 2 in an argand plane are:
(a) (b)
(b)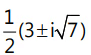 (c)
(c)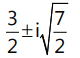
(d)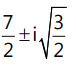
Ans: (b)
|z - 3| = 2: (x - 3)2 + y2 = 4
|z|=2: x2+y2 = 4
Points of intersection lie on the radical axis S1 - S2 = 0Radical axis is x = 3/2x2 + y2 = 4
Que 7: If z is a complex number of unit modulus and argument θ , then arg  equals(a)
equals(a)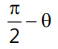
(b) θ
(c) π−θ
(d) −θ
Ans: (b)
Let θ = arg⇒ 0 = arg (z)
Que 8: If z1, z2 and z3 and are complex numbers such that 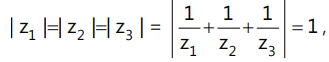 then |z1 + z2 + z3| is
then |z1 + z2 + z3| is
(a) Equal to 1
(b) Less than 1
(c) Greater than 3
(d) Equal to 3
Ans: (a)
Given, I Zl z2 z3 1=1
Now,IZI 12=1
⇒ IZ1I2=1
⇒Again now,
⇒
⇒
⇒ Iz1 + z2+ z3I = 1
Que 9: A value of θ for which 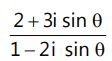 is purely imaginary, is:(a) π/6(b)
is purely imaginary, is:(a) π/6(b) 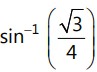 (c)
(c)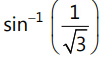 (d) π/3
(d) π/3
Ans: (c)
Que 10: Let a, b, c be distinct complex numberssuch that 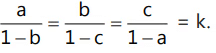 Find the value of k.
Find the value of k.
Ans:
a = k – kb
b = k – kc
c = k – ka
a = k – k2 + k2 (k – ka)a = k – k2 + k3 –k3 a)
but a ≠ b ≠ c
i.e. k3 = –1 ⇒ k = –w, –w2
|
172 videos|476 docs|154 tests
|
FAQs on Revision Notes: Complex Numbers - Mathematics (Maths) for JEE Main & Advanced
| 1. What are complex numbers and how are they represented? |  |
| 2. How do you add and subtract complex numbers? |  |
| 3. What is the modulus of a complex number and how is it calculated? |  |
| 4. How can complex numbers be multiplied? |  |
| 5. What are the applications of complex numbers in engineering and physics? |  |