Heat Transfer Class 11 Notes Physics
It was a very cold day, and the lab was only heated by a blower not making much difference. One of the professors climbed onto a table and stood there with his laptop doing his work. After ten minutes, someone asked if he wanted a chair. The professor declined, explaining that he was applying scientific methods. He pointed out that hot air rises, so the warmest spot in the room would be near the ceiling. The next moment everyone in the lab was standing up on their tables and doing their work. Indeed this was an excellent way to apply the concept of heat transfer and use it to solve a problem!
In this document, we will study heat transfer in detail.
What is Heat Transfer?
The movement of heat across the border of the system due to a difference in temperature between the system and its surroundings.
Interestingly, the temperature difference is said to be a ‘potential’ that causes the transfer of heat from one point to another. Heat can travel from one place to another in several ways. The three different modes of heat transfer include:
- Conduction
- Convection
- Radiation
Meanwhile, if a temperature difference exists between the two systems, heat will find a way to transfer from the higher to the lower system.
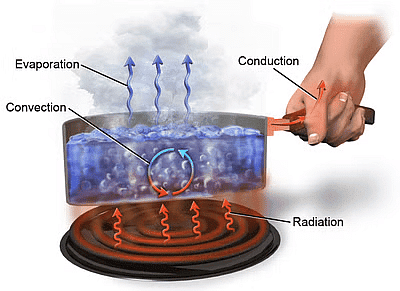 Modes of Heat Transfer
Modes of Heat Transfer
Conduction
Conduction is that mode of transmission of heat by which heat travels, through an unequally heated body, from the hot end to the cold end, from particle to particle, the particles themselves remaining at their mean positions.
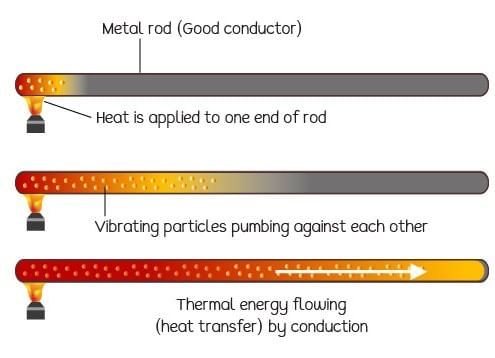 Conduction of heat in a metal rod
Conduction of heat in a metal rod
Following are the examples of conduction:
- The ironing of clothes is an example of conduction where the heat is conducted from the iron to the clothes.
- Heat is transferred from hands to ice cube resulting in the melting of an ice cube when held in hands.
- Heat conduction through the sand at the beaches. This can be experienced during summer. Sand is a good conductor of heat.
Conduction Equation
The coefficient of thermal conductivity shows that a metal body conducts heat better when it comes to conduction. The rate of conduction can be calculated by the following equation:
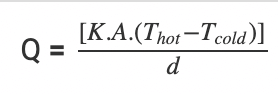
Where,
- Q is the transfer of heat per unit of time
- K is the thermal conductivity of the body
- A is the area of heat transfer
- Thot is the temperature of the hot region
- Tcold is the temperature of the cold region
- d is the thickness of the body
Q1. A 10 cm thick block of ice with a temperature of 0 °C lies on the upper surface of a 2400 cm2 slab of stone. The slab is steam-exposed on the lower surface at a temperature of 100 °C. Find the heat conductivity of stone if 4000 g of ice is melted in one hour given that the latent heat of fusion of ice is 80 cal/gm.
Solution:
Area of slab, A = 2400 cm2
Thickness of ice, d = 10 cm
Temperature difference, Th – Tc = 100 °C – 0 °C = 100 °C
Time of heat transfer, t = 1 hr = 3600 s
Amount of heat transfer, Q = m L = 4000 × 80 = 320000 cal
Heat transfer rate, q = Q ⁄ t = 320000 cal ⁄ 3600 s = 89 cal ⁄ s
The formula for heat transfer rate is given as:
q = K A (Th – Tc) ⁄ d
Rearrange the above formula in terms of K.
K = q d ⁄ A (Th – Tc)
= (89 × 10) ⁄ (2400 × 100) cal ⁄ cm s °C
= 3.7 × 10-3 cal/cm s °C
Hence, the thermal conductivity of stone is 3.7 × 10-3 cal/cm s °C.
Convection
It is defined as that mode of transmission of heat by which heat travels from one part of a body to another by the actual motion of the heated particles of the body.
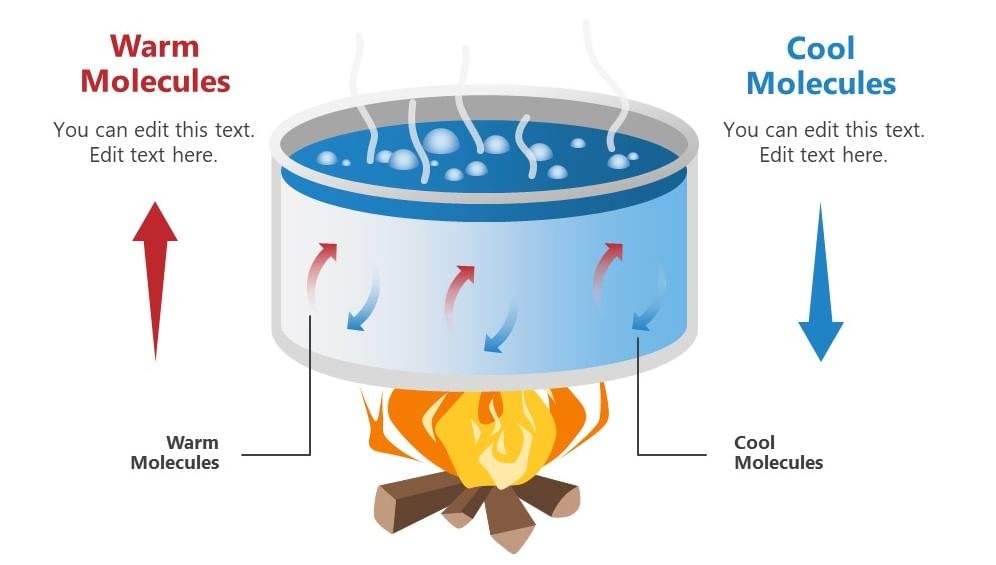 Convection in boiling water
Convection in boiling water
Examples of convection include:
- The boiling of water, that is molecules that are denser move at the bottom while the molecules which are less dense move upwards resulting in the circular motion of the molecules so that water gets heated.
- Warm water around the equator moves towards the poles while cooler water at the poles moves towards the equator.
- Blood circulation in warm-blooded animals takes place with the help of convection, thereby regulating the body temperature.
Convection Equation
As the temperature of the liquid increases, the liquid’s volume also has to increase by the same factor and this effect is known as displacement. The equation to calculate the rate of convection is as follows:
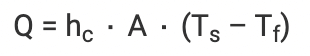
Where,
- Q is the heat transferred per unit of time
- Hc is the coefficient of convective heat transfer
- A is the area of heat transfer
- Ts is the surface temperature
- Tf is the fluid temperature
Q2. A fluid flows over a plane surface 1 m by 1 m. The surface temperature is 50oC, the fluid temperature is 20oC and the convective heat transfer coefficient is 2000 W/m2C. What is the convective heat transfer between the hotter surface and the colder air?
Solution:
Q = (2000 W/(m2 C)) ((1 m) (1 m)) ((50 oC) - (20 oC))
= 60000 (W)
= 60 (kW)
Radiation
The third means of energy transfer is radiation which does not require a medium. The best known
example of this process is the radiation from sun. All objects radiate energy continuously in the form
of electromagnetic waves.

Following are examples of radiation:
- Microwave radiation emitted in the oven is an example of radiation.
- UV rays coming from the sun are an example of radiation.
- X-rays from X-ray tubes are examples of radiation.
Radiant Energy
All bodies radiate energy in the form of electromagnetic waves by virtue of their temperature. This energy is called the radiant energy.
Radiation Equation
As temperature rises, the wavelengths in the spectra of the radiation emitted decrease, and shorter wavelength radiations are emitted. Thermal radiation can be calculated by the Stefan-Boltzmann law:

Where,
- P is the net power of radiation
- A is the area of radiation
- Tr is the radiator temperature
- Tc is the surrounding temperature
- e is emissivity and σ is Stefan’s constant (σ = 5.67 × 10-8Wm-2K-4)
Q3. What is the rate of heat transfer by radiation, with an unclothed person standing in a dark room whose ambient temperature is 22.0ºC? The person has a normal skin temperature of 33.0ºC and a surface area of 1.50 m2. The emissivity of skin is 0.97 in the infrared, where the radiation takes place.
Solution:
The Stefan-Boltzmann law is given by:
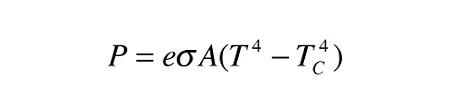 Given:
Given:
ε = 0.97 (emissivity of skin),
A = 1.50 m2 (surface area),
T = 22.0ºC + 273.15 = 295.15 K (ambient temperature),
Tc = 33.0ºC + 273.15 = 306.15 K (skin temperature).
Substituting these values into the equation, we have:
Q = 0.97 * (5.67 x 10-8 W/(m2K4)) * 1.50 m2 * ((295.15 K)4 - (306.15 K)4)
Calculating this expression will give us the rate of heat transfer by radiation (Q) in watts (W).
Q ≈ 0.97 * (5.67 x 10-8) * 1.50 * ((295.15)4 - (306.15)4) W
Please note that due to the complexity of the calculation, the final numerical value of Q may be quite small.
Temperature Gradient
It is defined as the rate of change of temperature of the different cross-section with distance.
Mathematically, the temperature gradient (∇T) can be defined as:
∇T = dT/dx
where ∇T represents the temperature gradient, dT represents the temperature change, and dx represents the change in distance along the coordinate axis (usually the x-axis).
Coefficient of Thermal Conductivity (K)
The coefficient of thermal conductivity (K) of the material of a rod is defined as the heat current (amount of heat flowing per second) flowing per unit area between two cross-sections of the rod each of area 1 m2 and separated 1 m apart.
Mathematically, the thermal conductivity (k) is defined as:
K = Ql/(A(θ1-θ2)t)
Dimension of K: [K] = [M1L1T-3K-1]
Unit: C.G.S- cal cm-1s-1 ºC-1
S.I.: Wm-1K-1
Rate of flow of heat = dQ/dt
Heat current, through a conducting rod, is defined as the amount of heat conducted across any cross-section of the rod in one second.
H= dQ/dt
H depends upon the following factors:
- Area of a cross-section of rod: H ∝ A
- Temperature Gradient: H ∝-dθ/dx
- Nature of the material
So, H = -KA (dθ/dx)
" Here K is called the coefficient of thermal conductivity of the material of the rod. It depends upon the nature of the material of the rod."
The total heat Q crossing from one cross-section to the other in time t:
Q = KA(θ1-θ2)t/l, where l is the length.
Or K = Ql/A(θ1-θ2)t
Q4. Calculate the thermal conductivity of a copper rod if a heat flux of 1000 W is conducted through a 2-meter length of the rod. The temperature difference between the ends of the rod is 50 degrees Celsius, and the cross-sectional area is 0.05 square meters.
Solution:
Heat flux (Q) = 1000 W
Length of the rod (l) = 2 m
Temperature difference (θ1 - θ2) = 50°C
Cross-sectional area (A) = 0.05 m²
We can use the formula for thermal conductivity:
K = Ql / (A * (θ1 - θ2))
Plugging in the values:
K = (1000 W * 2 m) / (0.05 m² * 50°C)
Simplifying:
K = 40 W/(m·°C)
Therefore, the thermal conductivity of the copper rod is 40 W/(m·°C).
Thermal Conductance (σh)
It is defined as heat current per unit temperature difference.
σh= KA/l
σh= H/dθ
Unit- S.I- WK-1
Thermal Resistance (RH)
The thermal resistance, of a conductor, is defined as the temperature difference between its two cross-sections when a unit heat current flows through it.
Reciprocal thermal conductance is known as the thermal resistance of the substance.
Rh= 1/σH = l/KA = dθ/H
Units of Rh: S.I – W-1K
The thermal resistance of a conductor of length d: RTH = d/KA
H= (θ1- θ2)/(l/KA) = (θ1- θ2)/Rh
Searle’s Method for K:
K= m(θ4- θ3)d/A(θ1- θ)t
The ratio of thermal and electrical conductivities is the same for the metals at a particular temperature and is proportional to the absolute temperature of the metal. If T is the absolute temperature, then
K/σ ∝ T or K/ σT = constant
Ingen Hausz Experiment:
K1/K2 = l12/ l22
Flow of heat through a composite slab:-
(a)Thermal resistance in series: The thermal resistance of the composite slab is equal to the sum of their thermal resistances.
(l1 +l2)/KA = (l1/K1A) + (l2/K2A)
Rcomb = Rh+Rh'
If l1=l2=l, then, K = 2K1K2/K1+K2
Temperature of the interface:-
θ0= [θ1Rh' + θ2Rh]/ [Rh+ Rh'] or θ0 = [θ1K1l2+ θ2 K2l1]/ [K1l2+ K2l1]
(b) Thermal resistance in parallel:- Reciprocal of the combination thermal resistance is equal to the sum of the reciprocals of individual thermal resistances.
1/Rcomb = 1/Rh + 1/Rh´
Reflecting Power (r)
The reflecting power (r) of a substance is defined as the ratio between the amount of heat reflected by the substance to the total amount of heat incident upon it.
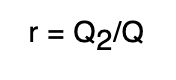
Transmitting power (t)
The transmitting power (t) of a substance is defined as the ratio between the amount of heat transmitted by the body to the total amount of heat incident upon it.
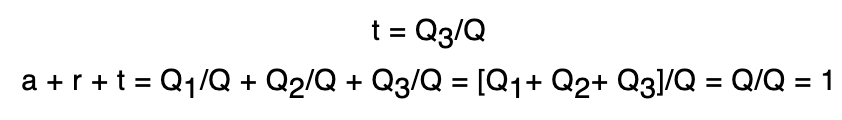
Radiant emittance (E)
Radiant emittance of a body at a temperature T is defined as the total amount of energy (for all wavelengths) radiated per unit time, per unit area by the body.
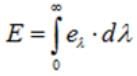
Unit - S.I: Jm-2s-1
C.G.S: erg cm-2s-1
Energy Density
The total energy density (U) at any point is defined as the radiant energy per unit volume, around that point, for wavelengths taken together.
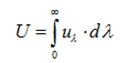 Now, let us define a few important terms related to Heat Transfer
Now, let us define a few important terms related to Heat Transfer
Basic Definitions and Terms Related to Heat Transfer
 |
Download the notes
Heat Transfer
|
Download as PDF |
Bolometer
A bolometer is a device for measuring the power of incident electromagnetic radiation via the heating of a material with a temperature-dependent electrical resistance.
If Rt and R0 are the resistances of the conductor at 0ºC and tºC, then, Rt = R0(1+αt), Here α is the temperature coefficient of change of resistance with temperature.
Absorptive power (a)
Absorptive power (a) of the substance is defined as the ratio between amounts of heat absorbed by it to the total amount of heat incident upon it.

Q5. A substance absorbs 400 J of heat when 800 J of heat is incident upon it. Calculate the absorptive power (a) of the substance.
Solution:
Given:
Heat absorbed (Q_absorbed) = 400 J
Total heat incident (Q_incident) = 800 J
The absorptive power (a) can be calculated using the formula:
a = Q_absorbed / Q_incident
Substituting the given values:
a = 400 J / 800 J
Calculating:
a = 0.5
Therefore, the absorptive power (a) of the substance is 0.5 or 50%. This means that the substance absorbs 50% of the total amount of heat incident upon it.
Spectral Absorptive Power (aλ)
Absorptive power refers to all wavelengths (total radiant energy). However, any surface will have different values of absorptive powers for different wavelengths.
- A surface may be a good absorber for wavelength λ1 and a bad absorber for wavelength λ2, which means its absorptive power for wavelength λ1 is greater than the absorptive power for λ2.
- Thus, spectral absorptive power aλ is defined as the ratio of the radiant energy of a given wavelength absorbed by a given surface in a given time to the total radiant energy of that wavelength incident at the same time on the same surface.
- Or we can say that it is absorptive power for that particular wavelength. It is now obvious that
a =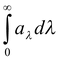
aλ ≤ 1
For a perfectly black body aλ = 1
Q6. 200 units of energy are incident on a surface. Out of this, 50 units are of wavelength λ1, 70 units are of wavelength λ2, and the remaining 80 units correspond to other wavelengths. The surface absorbs a total of 150 units of energy. Within this absorbed energy, 30 units are of wavelength λ1 and 40 units are of wavelength λ2. Find the absorptive power (a), spectral absorptive power for λ1 (aλ1), and spectral absorptive power for λ2 (aλ2).
Solution:
Given:
Total incident energy = 200 units
Energy absorbed by λ1 = 30 units
Energy absorbed by λ2 = 40 units
To find a, the total absorptive power:
a = (Energy absorbed) / (Total incident energy) = 150 units / 200 units = 0.75
To find aλ1, the spectral absorptive power for λ1:
aλ1 = (Energy absorbed by λ1) / (Energy incident at λ1) = 30 units / 50 units = 0.6
To find aλ2, the spectral absorptive power for λ2:
aλ2 = (Energy absorbed by λ2) / (Energy incident at λ2) = 40 units / 70 units = 0.57
From this example, we can observe that the total absorptive power (a) of the surface is 0.75. The spectral absorptive power for λ1 (aλ1) is 0.6, indicating that the surface is a good absorber of wavelength λ1. On the other hand, the spectral absorptive power for λ2 (aλ2) is 0.57, which is less than the total absorptive power (0.75). This suggests that the surface is a relatively poorer absorber of wavelength λ2 compared to λ1.
Q7. 100 units of energy are incident on a surface. In this 20 units are of wavelength λ1, 30 units are of wavelength λ2 and rest 50 units are other wavelengths. A total of 60 units of energy is absorbed by the surface. Of these 60 units, 5 units are of λ1 and 25 units are of λ2. Find a, 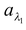 and
and 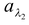 .
.
Solution:
Total absorptive power a = 60/100 = 0.6
and spectral absorptive power for λ1 = 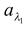 = 5/20 = 0.25
= 5/20 = 0.25
Spectral absorptive power for λ2 = 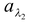 = 25/30 = 0.83
= 25/30 = 0.83
From this example, it is clear that the total absorption power of the surface is only 0.6 whereas 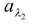 is 0.83 (> 0.6) i.e. the surface is a good absorber of wavelength λ2.
is 0.83 (> 0.6) i.e. the surface is a good absorber of wavelength λ2.
Emissive Power (e)
Emissive Power (e) refers to the amount of radiant energy emitted per second per unit area of a surface in the form of electromagnetic radiation.
For a black body e = σ T4
(Do not confuse it with the emissivity e which is different from it, although both have the same
symbol e).
- It represents the radiant intensity of the surface. The radiant intensity of a surface is influenced by its characteristics and temperature.
- The unit of measurement for radiant intensity is W/m² or J/s-m2. In the case of a perfectly black body, the radiant intensity is at its maximum.
Q8. A surface with a temperature of 500 K has an emissive power of 1000 W/m². Calculate the emissive power (e) for a black body at the same temperature.
Solution:
Temperature of the surface (T) = 500 K
The emissive power of the surface (e) = 1000 W/m²
The emissive power for a black body (e) can be calculated using the formula:
e = σ * T^4
where σ is Stefan's constant.
Substituting the given values:
e = 5.735 x 10^-8 W/m²-K^4 * (500 K)^4
Calculating:
e ≈ 5.735 x 10^-8 W/m²-K^4 * 62500000 K^4
e ≈ 3.584375 W/m²
Therefore, the emissive power (e) for a black body at the same temperature is approximately 3.584375 W/m². This indicates the amount of radiant energy emitted per second per unit area by the black body at the given temperature.
Emissivity (e)
Emissivity (e) is a property of a surface that indicates its relative emittance compared to a perfectly black body. The emissivity value can be represented as ε = e/E, where ε ranges between 0 and 1.
ε = e/E, 0 ≤ ε ≤1
- Emissivity values range between 0 and 1, with 0 representing low emittance and 1 representing high emittance.
- Emissivity does not have any specific units or dimensions associated with it.
- A perfectly black body has an emissivity value of 1, meaning it emits radiation at the highest possible level for its temperature.
- Emissivity provides information about how much energy a surface radiates compared to a perfectly black body under similar conditions. For example, if a surface has an emissivity of 0.6, it means that it emits 60% of the energy radiated by a perfectly black body at the same temperature and wavelength.
- Emissivity is defined as the ratio of the energy radiated from a material's surface to the energy radiated by a blackbody (perfect emitter) at the same temperature, wavelength, and viewing conditions.
- The emissivity of a material is numerically equal to its absorptive power, denoted by e = aλ.
- The emissivity of a body affects its radiant emittance, which is the total amount of radiant energy emitted per unit area per second.
- A perfectly black body, with an emissivity of 1, emits the maximum amount of radiant energy for its temperature and is considered an ideal emitter.
- In contrast, the emissivity of any other body, which is not a perfectly black body, is always less than one, indicating a lower level of emittance.
Spectral Emissive Power (eλ)
Spectral emissive power is defined as the rate at which radiation of wavelength l is emitted in all directions form a surface per unit wavelength dl about l. In Simpler terms, It is emissive power of the surface for a particular wavelength λ.
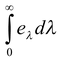
eλ is the maximum for a perfectly black body.
Q9. The spectral emissive power E for a body at temperature T is planted against the wavelength and the area under the curve is found to be A. At a different temperature, T2 the area is found to be 9A. Then λ1/λ2 =
Solution: 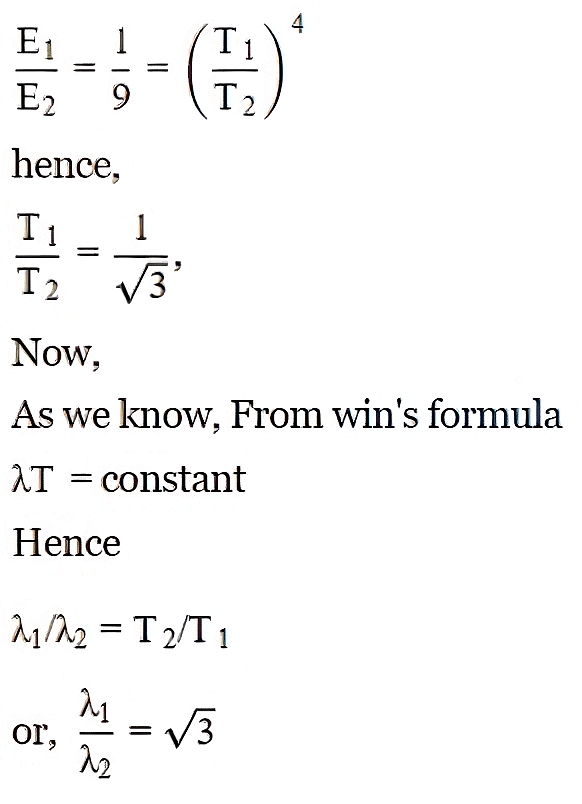
Stefan’s Law
Radiant emittance or the energy radiated per second per unit area by a perfect black body varies directly as the fourth power of its absolute temperature.
E = σT4
Here σ is Stefan’s constant and its value is 5.735×10-8 Wm-2K-4
Q10. A black body has an absolute temperature of 300 K. Calculate the radiant emittance of the body.
Solution:
Given:
Absolute temperature (T) = 300 K
Stefan's constant (σ) = 5.735 × 10-8 Wm-2K-4
Using Stefan's Law:
E = σT4
Substituting the values:
E = (5.735 × 10-8 Wm-2K-4)(300 K)4
Calculating:
E ≈ 12.93 W/m2
Therefore, the radiant emittance of the black body is approximately 12.93 W/m2.
Q11. The radiant emittance of a black body is 50 W/m^2. Find the absolute temperature of the body.
Solution:
Given:
Radiant emittance (E) = 50 W/m2
Stefan's constant (σ) = 5.735 × 10-8 Wm-2K-4
Using Stefan's Law:
E = σT4
Rearranging the formula:
T4 = E / σ
Substituting the values:
T4 = (50 W/m2) / (5.735 × 10-8 Wm-2K-4)
Calculating:
T4 ≈ 8.719 × 1015 K4
Taking the fourth root of both sides:
T ≈ 238.6 K
Therefore, the absolute temperature of the black body is approximately 238.6 K.
Perfectly Black Body
A body that absorbs all the radiation incident upon it and has an emissivity equal to 1 is called a perfectly black body.
- A black body is also an ideal radiator. It implies that if a black body and an identical other body are kept at the same temperature, then the black body will radiate maximum power as is obvious from equation P = eAσ T4 also.
- Because e =1 for a perfectly black body while for any other body e <1.
Kirchhoff’s law of Heat Radiation
It states that at any temperature, the ratio of emissive power eλ of a body to its absorptive power aλ, for a particular wavelength, is always constant and is equal to the emissive power of a perfect black body for that wavelength.
eλ/aλ = Constant = Eλ
This implies the ratio between eλ and aλ for anybody is a constant quantity (= Eλ).
Q12. At a particular temperature and wavelength, the spectral emissive power and monochromatic absorptive power of a body are 10 and 8 units respectively. What will be the emissive power of a black body at the same temperature?
Solution: According to Kirchoff's law.
eλ/aλ = Constant = Eλ
here, we are given that eλ= 10 and aλ = 8
So, Eλ= 10/8 = 1.25
Q13. At a temperature of 500 K, a body has a spectral emissive power of 20 W/m²·nm and a monochromatic absorptive power of 15 W/m²·nm at a specific wavelength. According to Kirchoff's Law of Heat Radiation, what is the value of the emissive power of a black body at the same temperature and wavelength?
Solution:
To find the emissive power of a black body at the same temperature and wavelength, we can use Kirchoff's Law of Heat Radiation, which states that the ratio of spectral emissive power (eλ) to monochromatic absorptive power (aλ) at a given temperature and wavelength is constant.
Given:
Temperature (T) = 500 K
Spectral emissive power (eλ) = 20 W/m²·nm
Monochromatic absorptive power (aλ) = 15 W/m²·nm
Using Kirchoff's Law, we have:
eλ/aλ = Constant = Eλ (emissive power of a black body)
Substituting the given values:
Eλ = eλ/aλ = 20 W/m²·nm / 15 W/m²·nm = 1.33
Therefore, the emissive power of a black body at the same temperature and wavelength is 1.33 W/m²·nm.
Cooling by Radiation
If a body having temperature T is kept in an environment of temperature To (< T), the body will lose energy at a rate
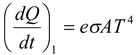
and absorb energy at a rate
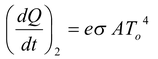
Thus, the net rate of loss of energy
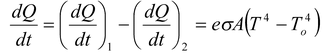
If m is the mass of the body and c is its specific heat, the rate of loss of heat at temperature T must be
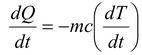
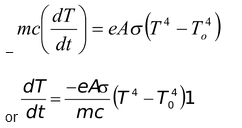
Thus, the rate of cooling (dT/dt) depends on A, m, c, T, To, and e ( i.e. nature of the radiating surface). Hence greater the emissivity faster the cooling.
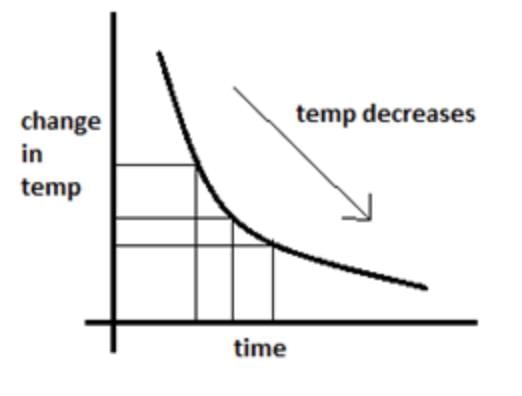
Newton’s Law of Cooling
The rate of cooling of a body is directly proportional to the difference in temperature of the body over its surroundings.
If a body at temperature θ1 is placed in surroundings at lower temperature θ2, the rate of cooling is given by:
dQ/ dt ∝ (θ1 −θ2) where dQ is the quantity of heat lost in time dt.
Newton’s law of cooling gives
dQ /dt = −k(θ1−θ2) where k is constant.
If a body of mass m and specific heat s loses a temperature dθ in time dt, then
dQ /dt =ms(dθ/dt) =−k(θ1−θ2)
Q14. A liquid cools from 70℃ to 60℃ in 5 minutes. Calculate the time taken by the liquid to cool from 60℃ to 50℃, if the temperature of the surroundings is constant at 300C. (JEE Mains, 2022)
Solution:
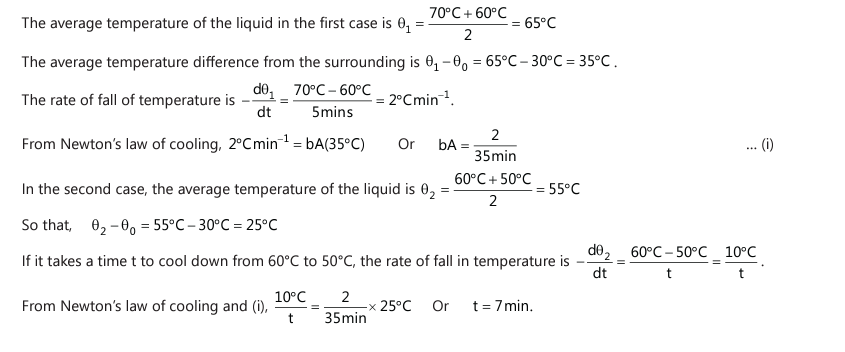 Q15. A body at a temperature of 40ºC is kept in a surrounding of constant temperature of 20ºC. It is observed that its temperature falls to 35ºC in 10 minutes. Find how much more time will it take for the body to attain a temperature of 30ºC. (JEE Mains, 2022)
Q15. A body at a temperature of 40ºC is kept in a surrounding of constant temperature of 20ºC. It is observed that its temperature falls to 35ºC in 10 minutes. Find how much more time will it take for the body to attain a temperature of 30ºC. (JEE Mains, 2022)
Solution:
From Newton’s law of cooling, qf = qi e-kt
Now, for the interval in which temperature falls from 40 to 35oC.
(35 – 20) = (40 – 20) e-k.10
e-10k = 3/4
k = [ln 4/3]/10 . . . . (a)
Now, for the next interval,
(30 – 20) = (35 – 20)e-kt
e-kt = 2/3
kt = ln 3/2 . . . . (b)
From equations (a) and (b),
t = 10 × [ln(3/2)/ln(4/3)]= 14.096 min.
Wien’s Displacement Law
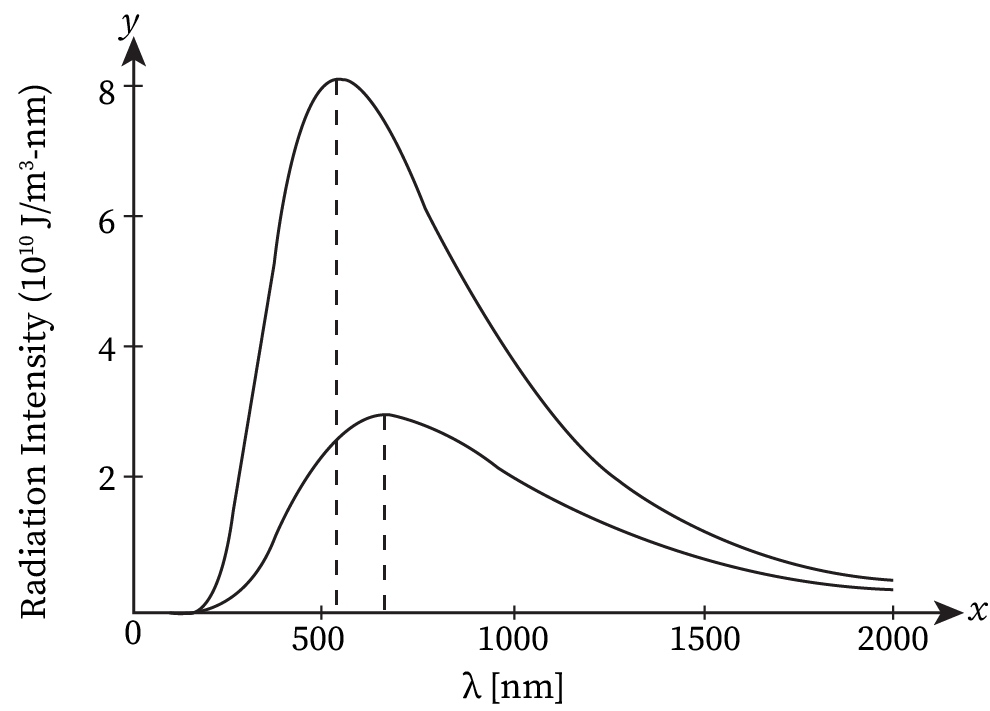
When things are not too hot (below around 600℃), the heat radiation they give off can't be seen by our eyes because it's mostly in longer wavelengths than what we can see. The graph illustrates how the energy from this heat radiation changes with temperature and wavelength. As the temperature rises, two things happen. First, the highest point in the energy distribution moves to shorter wavelengths. This shift follows a rule called Wien's displacement law.
It states that the wavelength of radiation that is emitted with maximum intensity varies inversely to the absolute temperature of the body.
λm×T = Constant
The value of this constant in S.I. units is 2.898 × 10−3 m-K
Have you ever wondered how scientists calculate the temperature of the sun and other stars? It is through this law.
Q16. A black body has a maximum intensity wavelength of 500 nm. According to Wien's Displacement Law, if the absolute temperature of the body is 4000 K, what would be the constant value?
Solution:
According to Wien's Displacement Law, the product of the wavelength of radiation emitted with maximum intensity (λm) and the absolute temperature (T) of a black body is a constant value.
Given:
Maximum intensity wavelength (λm) = 500 nm
Absolute temperature (T) = 4000 K
Using the formula:
λm × T = Constant
Substituting the values:
Constant = 500 nm × 4000 K
Solving for the constant value:
Constant = 2,000,000 nm·K
Therefore, the constant value is 2,000,000 nm·K.
Q17. What is the wavelength of the brightest part of the light from our next closest star, Proxima Centauri? Proxima Centauri is a red dwarf star about 4.2 light years away from us with an average surface temperature of 3,042 Kelvin. (JEE Mains, 2021)
Solution:
λmax = T b
We don’t need the distance to solve this. All we need is the surface temperature to plug into our Wien’s law equation.
Wavelength λmax in meters = 0.0029m-K / 3042K; which is 0.000000953 meters.
We can convert this to nanometers and we get a peak wavelength of 953 nm.
Q18. The maximum intensity wavelength of radiation emitted by a black body is 700 nm. According to Wien's Displacement Law, if the constant value is 3,000,000 nm·K, what would be the absolute temperature of the body?
Solution:
According to Wien's Displacement Law, the product of the wavelength of radiation emitted with maximum intensity (λm) and the absolute temperature (T) of a black body is a constant value.
Given:
Maximum intensity wavelength (λm) = 700 nm
Constant value = 3,000,000 nm·K
Using the formula:
λm × T = Constant
Substituting the values:
700 nm × T = 3,000,000 nm·K
Solving for the absolute temperature:
T = 3,000,000 nm·K / 700 nm
T ≈ 4285.7 K
Therefore, the absolute temperature of the black body is approximately 4285.7 K.
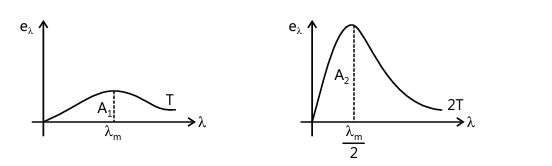
Q19. Two bodies A and B have thermal emissivity of 0.1 and 0.81 respectively. The outer surface areas of the two bodies are identical. These two bodies emit total radiative power at the same rate. The wavelength λB corresponding to the maximum spectral radiancy in the radiation from B is 1.0 µm larger than the wavelength λA corresponding to the maximum spectral radiancy in the radiation from A. If the temperature of body A is 5802 K, find (JEE Mains, 2021)
(a) the temperature of (B)
(b) λB
Solution:
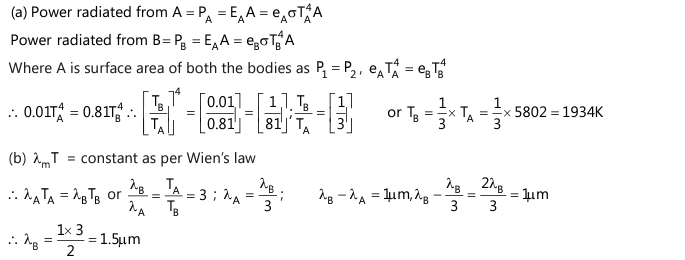
Wein’s Radiation Law
Wien's displacement law states that the black body radiation curve for different temperatures peaks at a wavelength inversely proportional to the temperature.
Eλdλ = (A/λ5) f(λT) dλ = (A/λ5) e-a/λT dλ
The rate of cooling of water increases with a fall in temperature.
Solar Constant
The solar constant is how much sunlight the Earth gets in one minute on each square centimeter of a surface directly facing the sun at an average distance from it. If we ignore the absorption of sunlight by the Earth's atmosphere, the solar constant, denoted as 'S,' is calculated to be 1.94 cal/cm2/min.
The temperature of the sun, T, is given as follows :
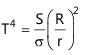 Where S is the solar constant, σ is Stefan’s constant, R is the mean distance of the earth from the sun and r is the radius of the sun.
Where S is the solar constant, σ is Stefan’s constant, R is the mean distance of the earth from the sun and r is the radius of the sun.
FAQs on Heat Transfer Class 11 Notes Physics
| 1. What is Stefan’s Law in heat transfer? |  |
| 2. What is Kirchhoff’s law of Heat Radiation in heat transfer? |  |
| 3. How does cooling by radiation work in heat transfer? |  |
| 4. What is Newton’s Law of Cooling in heat transfer? |  |
| 5. What is Wien’s Displacement Law in heat transfer? |  |