Methods of Enquiry in Psychology Class 11 Psychology
| Table of contents |

|
| Goals of Psychological Enquiry |

|
| Nature of Psychological Data |

|
| Some Important Methods in Psychology |

|
| Research Methods in Psychology |

|
| Limitations of Psychological Enquiry |

|
| Ethical Issues |

|
Goals of Psychological Enquiry
Like any scientific research, psychological enquiry aims to objectively achieve the following goals: description, prediction, explanation, control of behaviour, and practical application of the knowledge gained. This chapter will help you understand these goals, the types of data collected in psychological studies, the various methods used in psychology, and key issues related to these studies. Psychologists employ different research methods because human behaviour is complex, and no single method can address all questions.
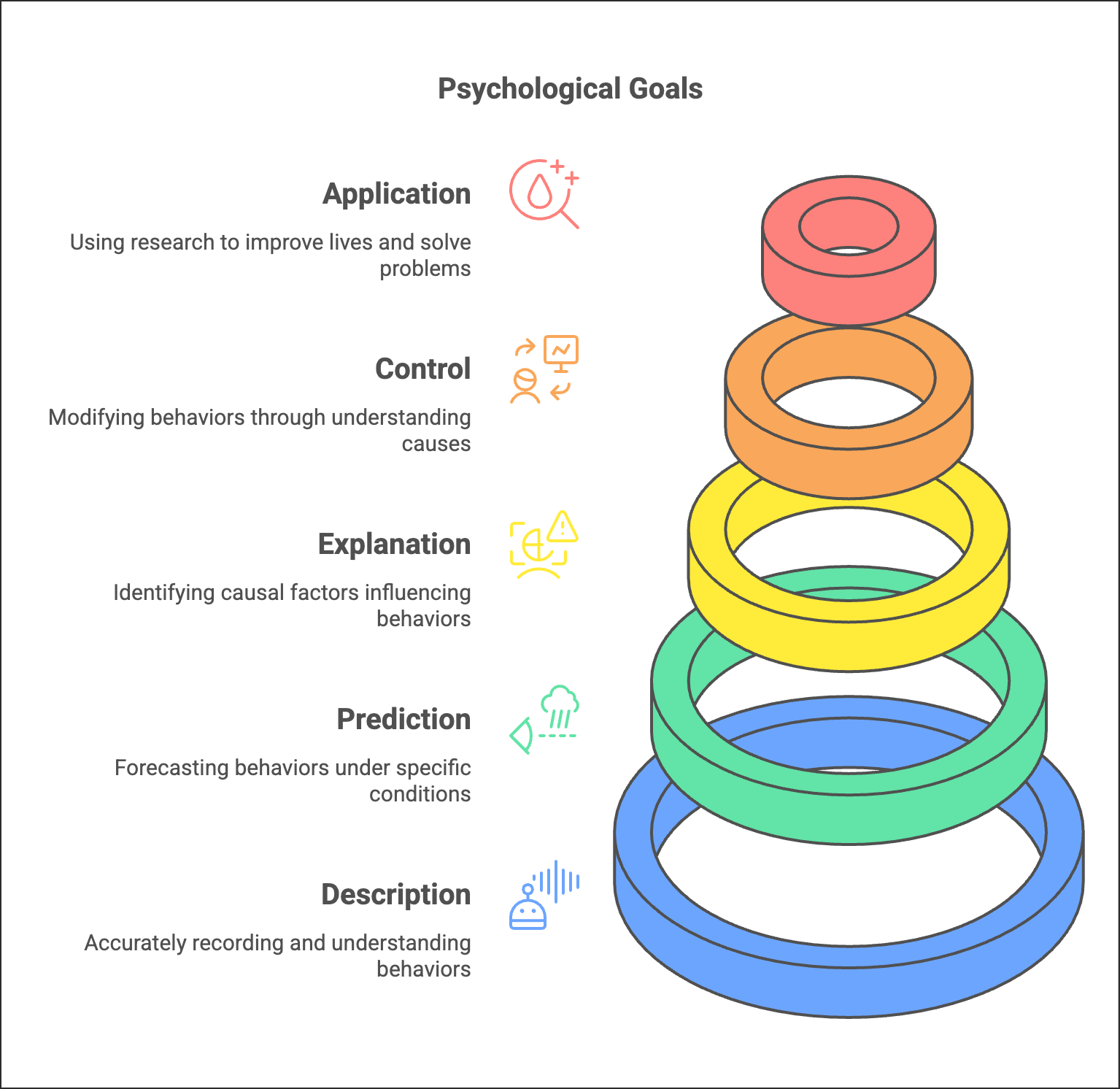
Description:
- In psychological research, the primary aim is to accurately describe behaviours or phenomena, distinguishing them from others.
- For instance, when studying student study habits, descriptions may include attending classes regularly, submitting assignments on time, and following a study schedule.
- Detailed recording of behaviours aids in proper understanding.
Prediction:
- The goal here is to predict behaviours based on understanding and accurate descriptions.
- By establishing relationships between behaviours and events, researchers can forecast likely behaviours under specific conditions.
- For example, more study time may predict better academic performance.
Explanation:
- Psychological inquiry aims to identify the causal factors influencing behaviours.
- Understanding why behaviours occur helps establish cause-effect relationships.
- Factors influencing behaviours, such as attentiveness in class or study habits, are explored.
Control:
- By understanding the causes of behaviours, researchers can aim to control, enhance, or reduce them.
- Changes in antecedent conditions can lead to changes in behaviour.
- Psychological interventions like therapy exemplify control over behaviours.
Application:
- The ultimate goal is to use psychological research to improve people's lives and solve problems.
- Applications include using practices like yoga and meditation to reduce stress and enhance well-being.
- Psychological research also contributes to developing new theories and constructs for further study.
Steps in Conducting Scientific Research
- Science is characterized not by what it studies but by the way it conducts investigations, with the scientific method aiming to explore events or phenomena objectively, systematically, and in a testable manner.
- Objectivity in scientific research means that independent studies by different individuals should ideally lead to similar conclusions, much like how two people measuring the length of a table with the same device would likely reach the same result.
- Scientific research involves a systematic process, encompassing steps such as defining a problem, gathering data, making conclusions, and refining research outcomes and theories.
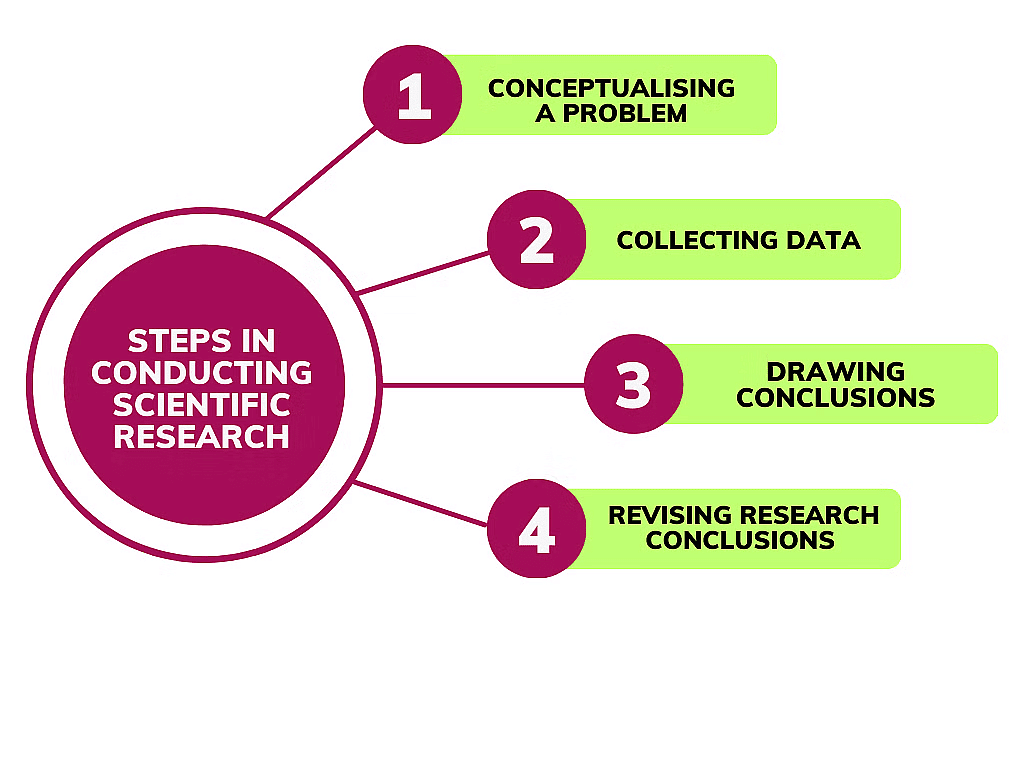
The steps in conducting scientific research are:
- Conceptualising a Problem: Research begins with the researcher picking a topic, refining their focus, and developing specific research questions based on previous studies, observations, and personal experiences.
- Collecting Data: This step involves creating a research design or plan for the study. Key decisions must be made regarding:
- participants involved in the study,
- methods of data collection,
- tools for data collection, and
- how these tools will be used (individually or in groups).
- Drawing Conclusions: Next, researchers analyse the collected data using statistical techniques to interpret what the data reveals. This can involve creating graphs (like pie charts and bar diagrams) and applying various statistical methods. The aim of this analysis is to confirm a hypothesis and draw conclusions based on the findings.
- Revising Research Conclusions: Researchers assess if their results support the initial hypotheses, making revisions or suggesting new theories as needed.
Alternative Paradigms of Research
- Views human behavior as predictable, influenced by internal and external forces.
- Focuses on observable and measurable behavior, excluding personal feelings and experiences.
- Emphasizes on methods akin to physical sciences like physics, chemistry, and biology.
Interpretive Research Paradigm:
- Values understanding over prediction and explanation.
- Recognizes the complexity and variability of human behavior.
- Highlights the subjective interpretation of reality, giving importance to personal meanings and contexts.
- Advocates for exploring human experiences without disrupting their natural flow.
Personal Reflection and Psychological Inquiry:
- Encourages self-analysis of personal experiences, thoughts, and behaviors.
- Stresses the importance of psychology in understanding one's own actions and motivations.
- Promotes reflection on personal insights and experiences for self-understanding.
Nature of Psychological Data
- You may want to consider how psychological data are different as compared to other sciences.
- Psychologists collect a variety of information from different sources employing diverse methods.
- The information, also called data (singular = datum), relate to the individuals' covert or overt behaviour, their subjective experiences, and mental processes.
- Data form an important input in psychological enquiry, approximating reality to some extent and providing an opportunity to verify or falsify ideas, hunches, notions, etc.
- Data are not independent entities; they are located in a context and tied to the method and theory that govern the data collection process.
- Data are influenced by the physical or social context, the persons involved, and the time when the behaviour occurs.
- People behave differently in various situations based on factors such as being alone or in a group, at home or in the office.
- The method of data collection (survey, interview, experiment, etc.) and respondent characteristics influence the nature and quality of data.
- Data do not inherently speak about reality; inferences must be made by researchers placing data within its proper context.
Types of Data in Psychology
- Demographic Information: Includes personal details like name, age, gender, birth order, education, occupation, marital status, and more.
- Physical Information: Involves details about ecological conditions, housing, transportation, and facilities available.
- Physiological Data: Includes physical, physiological, and psychological data like height, weight, heart rate, EEG readings, blood pressure, and more.
- Psychological Information: Relates to intelligence, personality, emotions, psychological disorders, consciousness, and subjective experiences.
Some Important Methods in Psychology
Psychologists employ various methods like Observation, Experimental, Correlational, Survey, Psychological Testing, and Case Study to gather data.
1. Observational Method
- Observation is a potent tool in psychological research, used to describe behavior effectively.
- A scientific observation involves:
1. Selection: Psychologists choose specific behaviours to observe.
2. Recording: Researchers record observed behaviours using methods like tallies, notes, photographs, or video recordings.
3. Analysis of Data: After recording observations, psychologists analyze the data to derive meaning. - Effective observation requires skill, including knowing what to look for, whom to observe, when and where to observe, how to record observations, and methods for analyzing behaviour.

Types of Observation:
- Naturalistic vs Controlled Observation: Naturalistic observation occurs in real-life settings. The observer does not try to control or manipulate the situation. This type of observation happens in hospitals, homes, schools, day care centers, etc while controlled observation is conducted in controlled environments like laboratories.
- Non-Participant vs Participant Observation: In non-participant observation involves observing from a distance. Researchers watch subjects without actively participating in the situation. There is a risk that the act of observing may alter the behaviour of those being observed. While participant observation involves becoming part of the group being observed. It involves building rapport with the group to be accepted as a member.
Advantages and Disadvantages
- The observation method allows researchers to study people and their behaviour in natural settings as it unfolds.
- The observation method is labour-intensive, time-consuming, and can be influenced by the observer's biases.
- Observers should record behaviour as it occurs without interpreting it during the observation itself.
2. Experimental Method
- Experiments establish cause-effect relationships between variables in a controlled setting.
- Changes in one factor are studied for their effects on another factor, while keeping other factors constant.
- Cause refers to the manipulated event, while the effect is the resulting behaviour change.

The Concept of Variable
- A variable is any stimulus or event that varies and can be measured.
- Attributes of objects, rather than objects themselves, are variables.
- Variables can be of many types, including independent and dependent variables.
- Independent variables are manipulated by researchers in experiments, affecting dependent variables.
- Dependent variables represent the phenomenon being studied.
- Both types of variables are chosen based on the researcher's theoretical interest.
Experimental and Control Groups
- Experiments involve experimental groups exposed to manipulated variables and control groups without these manipulations.
- Conditions are kept constant for both groups, except for the manipulated variable.
- Control techniques are used to minimize the impact of extraneous variables.
Strength and Limitation
- Well-designed experiments offer convincing evidence of cause-effect relationships.
- However, they are often criticized for lacking external validity and real-world applicability.
- Laboratory experiments face challenges in controlling all relevant variables and may not always be feasible.
Field Experiments and Quasi Experiments
Field Experiments
- If a researcher desires high generalizability or needs to study phenomena not replicable in labs, they may opt for field settings.
- Typically more time-consuming and costly than lab experiments.
- Many variables are difficult to manipulate in lab settings.
Quasi Experimentation
- In quasi experiments, the independent variable is chosen rather than actively manipulated by the researcher.
- This method involves manipulating an independent variable in a natural setting using naturally occurring groups for experimental and control groups.
4. Correlational Research
- The strength and direction of the relationship between two variables are indicated by the correlation coefficient.
- A positive correlation implies that as one variable (X) increases, the other variable (Y) also increases.
- Conversely, a negative correlation suggests that as X goes up, Y goes down.
- Correlation coefficient ranges from -1.0 to 1.0, indicating positive, negative, or zero correlation.
- Positive correlation: both variables increase or decrease together.
- Negative correlation: one variable increases while the other decreases.
- Zero correlation: no significant relationship between variables.
5. Survey Research
- Originally used for studying opinions, attitudes, and social facts.
- Evolved to infer causal relationships.
- Techniques include personal interviews, questionnaires, telephonic surveys, and observations.
Personal Interviews
- Interviews are common for gathering information, opinions, attitudes, and reasons for behavior.
- Structured interviews have predetermined questions and fixed responses.
- Unstructured interviews allow flexibility in questioning and responses.
- Types: Individual to Individual, Individual to Group, Group to Individuals, Group to Group.
Questionnaire Survey
- Questionnaires are a common, flexible, and cost-effective way to collect information.
- They contain set questions that respondents answer in writing, which can be either open or closed.
- Respondents may rate statements on a scale of 3-point (Agree, Undecided, Disagree), 5-point (Strongly Agree, Agree, Undecided, Disagree, Strongly Disagree), or other scales.
- A challenge with mailed questionnaires is the potential for low response rates.
 Questionnaire Survey
Questionnaire Survey
Telephone Survey
- Respondents may be uncooperative or provide superficial answers since they do not know the interviewer.
- Those who respond may differ from those who do not, which could result in biased outcomes based on age, gender, income, education, and other psychological traits.
Considerations
- Each method has its own strengths and weaknesses; therefore, researchers must choose carefully.
- Surveys allow for quick data collection from many individuals and provide rapid insights into public opinions.
- However, participants may give inaccurate information due to memory issues or may not wish to disclose their true opinions. Some may provide answers they think the researcher desires.
Psychological Testing
- Understanding individual differences has always been a key focus in psychology.
6. Psychological Testing
- The evaluation of individual differences has always been a major aspect of psychology.
- Psychologists have developed a variety of tests to assess different human traits, such as intelligence, personality, and interests. These tests serve many purposes, including selection, placement, training, guidance, and diagnosis across various settings like schools, clinics, and workplaces.
- A psychological test usually contains questions (items) focused on a specific human trait, which must be clearly defined. All items should be related to that trait only.
- This type of test is an objective method used to compare people's mental or behavioural characteristics.
- Creating a test involves several steps, including item analysis, and checking for reliability, validity, and norms. Reliability assesses how consistent the scores are across different test sessions, while validity ensures the test measures what it is supposed to.
- Standardization involves setting benchmarks for tests so that an individual's performance can be compared with that of a group.
- Tests can be tailored for specific age groups and may be speed tests (with time limits) or power tests (without time limits).
Types of Tests
- Psychological tests are categorized based on language, mode of administration, and difficulty level.
- Verbal, non-verbal, and performance tests are classified based on language requirements.
- Tests can be individual (face-to-face administration) or group tests (administered to multiple individuals simultaneously).
- Tests can also be speed tests (with time limits) or power tests (without time limits).
- Tests should be chosen carefully, considering various factors alongside test data, like background and interests.
7. Case Study
- Case studies involve a thorough investigation of specific instances in psychology to understand different behaviours and phenomena.
- Researchers examine individuals, groups, organisations, or events, gathering detailed information through various methods like interviews and observations.
- This method is essential in clinical psychology and human development. For instance, Freud's ideas that formed psychoanalytic theory came from his detailed notes on individual cases. Likewise, Piaget's cognitive development theory was based on his observations of his own children.
- Studies have also looked into children's socialisation, like Minturn and Hitchcock's work on Rajputs in Khalapur and S. Anandalakshmy's study of childhood in a weavers community in Varanasi.
- While case studies provide rich insights into people's lives, caution is needed when making generalisations, as validity is often a challenge.
- It is advisable to select unique cases that offer a wealth of information. A case study uses various methods, such as interviews, observations, and psychological tests, to gather data from different sources related to the case.
- Psychologists employ case studies to explore feelings, fantasies, fears, and traumatic experiences, which enhances understanding of a person's mind and behaviour.
- After data collection, researchers analyse the information to draw conclusions. Quantitative methods use statistics for conclusions, while qualitative methods include narrative and content analysis.
- Some limitations of psychological research include the absence of an absolute zero point, the subjective nature of psychological tools, and the interpretation of qualitative data. Researchers must adhere to ethical standards, ensuring voluntary participation, informed consent, and sharing findings with participants.

Research Methods in Psychology
- After collecting data, researchers need to draw conclusions through analysis.
- Two main approaches for data analysis are quantitative and qualitative methods.
Quantitative Method
- Involves close-ended questions in tests, questionnaires, and structured interviews.
- Responses are usually scaled to indicate strength and magnitude.
- Answers are assigned numerical values for scoring.
- Calculations of scores help in understanding participants' levels on specific attributes.
- Statistical methods such as central tendency, variability, and correlation are utilized for analysis.
Qualitative Method
- Focuses on the complexity of human experiences.
- Utilizes methods like Narrative Analysis to understand experiences.
- Data in qualitative methods are descriptive and cannot be quantified.
- Content analysis is used to identify thematic categories in qualitative data.
Limitations of Psychological Enquiry
- Lack of True Zero Point: In physical sciences, measurements start from zero. For example, measuring the length of a table can begin at zero, allowing us to say it is 3' long. However, psychological measurements lack a true zero point. No one has zero intelligence; everyone has some level of intelligence. Psychologists arbitrarily set a point as zero and then measure from there. Consequently, scores in psychological studies are not absolute; they are relative.
- Relative Nature of Psychological Tools: Psychological tests are designed with specific contexts in mind. For instance, a test for urban students may include items that require knowledge of urban experiences. Tests need to be adjusted for different contexts.
- Subjective Interpretation of Qualitative Data: The interpretation of qualitative data can vary among researchers and participants. It is advisable to involve multiple researchers during fieldwork to agree on interpretations. Researchers must adhere to ethical principles, including voluntary participation, informed consent, and sharing results with participants.
Issues with Ranking in Assessments:
In some studies, ranks are used as scores. For example, a teacher may rank students based on test scores: 1, 2, 3, 4, and so on. The issue arises because the difference between the first and second rank may not be the same as between the second and third. For instance, the top student might score 48, the second 47, and the third 40. This shows that the differences in scores are not consistent, highlighting the relative nature of psychological measurement.
The lack of an absolute zero point, the relative nature of psychological tools, and the subjective interpretation of qualitative data are key limitations of psychological enquiry.
Ethical Issues
In psychological research, ethical guidelines are crucial to ensure the well-being and rights of participants. Several key ethical principles include:
 Ethical Issues
Ethical Issues
- Voluntary Participation: Participants must choose to be part of a study freely, without any pressure. They should be able to withdraw from the study at any time without penalty.
- Informed Consent: Before collecting data, participants need to be made fully aware of the study's procedures and any risks involved. Their consent must be obtained prior to data collection.
- Debriefing: After the study, participants should receive explanations to ensure they understand the research. This is especially important if any deception was used. Debriefing helps ensure participants leave in the same mental and physical state as when they arrived. Researchers should address any anxiety or negative feelings caused by the deception.
- Sharing Results: Researchers are required to return to participants and share the study's findings. This promotes transparency and allows participants to give feedback, which can lead to valuable insights.
- Confidentiality of Data: Protecting the privacy of participants is crucial. Researchers must keep data confidential, ensuring that participants' identities are safe throughout and after the study. The information should only be used for research purposes and must not be shared with others.
- Beneficence: Researchers must safeguard participants from harm and ensure their welfare during the study.
- Justice: This principle ensures that the benefits of research are shared fairly among all participants, promoting equal treatment.
|
43 videos|88 docs|18 tests
|
FAQs on Methods of Enquiry in Psychology Class 11 Psychology
| 1. What are the main goals of psychological enquiry? |  |
| 2. What types of data are commonly used in psychology? |  |
| 3. What are some important methods used in psychological research? |  |
| 4. How is data analyzed in psychological research? |  |
| 5. What are some ethical issues in psychological enquiry? |  |
















