Revision Notes: Number System | Mathematics Class 6 ICSE PDF Download
| Table of contents |

|
| What is a Number? |

|
| Approximation (Rounding Off) |

|
| Number System |

|
| Tests of Divisibility |

|
| Estimation |

|
| Roman Numerals |

|
| Metric System Conversions |

|

What is a Number?
- A number is a value used to count, measure, or label things.
For example, 5 apples or 10 books. - A numeral is a symbol that represents a number.
For example, the numeral "31" represents the number thirty-one. - Numeration is writing a number in words.
For example, the number 31 is written as "thirty-one."
Hindu-Arabic Numeration System
- This system uses digits 0 to 9 to form numbers.
- Each digit's value depends on its position in the number.
- For example, 98, 76, 54, 321 are numbers in the Hindu-Arabic system.
The place values in this system are:
Example: The place values In the number 54,321 are as follows
- 5 is in the ten thousands place: 5 × 10,000 = 50,000
- 4 is in the thousands place: 4 × 1,000 = 4,000
- 3 is in the hundreds place: 3 × 100 = 300
- 2 is in the tens place: 2 × 10 = 20
- 1 is in the ones place: 1 × 1 = 1
International Numeration System
- This system is used in many countries and also uses digits 0 to 9, but the place values are grouped differently.
- For example: 987,654,321 is written as 987 million, 654 thousand, 321 in the International system.
The place values are:

Example: The place values in the number 987,654,321 are as follows
- 9 is in the hundred millions place: 9 × 100,000,000 = 900,000,000
- 8 is in the ten millions place: 8 × 10,000,000 = 80,000,000
- 7 is in the millions place: 7 × 1,000,000 = 7,000,000
- 6 is in the hundred thousands place: 6 × 100,000 = 600,000
- 5 is in the ten thousands place: 5 × 10,000 = 50,000
- 4 is in the thousands place: 4 × 1,000 = 4,000
- 3 is in the hundreds place: 3 × 100 = 300
- 2 is in the tens place: 2 × 10 = 20
- 1 is in the ones place: 1 × 1 = 1
Place Value and Face Value
- Place Value:
The value of a digit based on its position in a number.
For example, In 4,603, the place value of 6 is 6 × 100 = 600 (hundreds place). - Face Value:
The value of the digit itself, regardless of its position.
For example, in 4,603, the face value of 6 is simply 6.
Approximation (Rounding Off)
- Approximation means finding a number that is close to the original number but easier to use. We round off numbers based on the digit in the place we are rounding to.
Rule for Rounding:
- If the digit to the right of the place you are rounding to is 5 or more, round up (add 1 to the place value).
- If the digit is less than 5, round down (keep the place value the same).
Example: Rounding the number 12,345 to different place values:
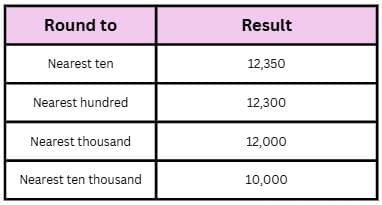
Number System

- Real Numbers (R): This set includes all negative and positive numbers, zero, and fractions, such as -2, 5, 0, 2/3, -4/5.
- Integer (Z): Examples of integers are -3, 2, -1, 0, 1, 2, 3.
- Whole Numbers (W): This set includes 0, 1, 2, 3, and so on, extending infinitely in the positive direction.
- Natural Numbers (N): These are the counting numbers starting from 1, 2, 3, and so forth, continuing indefinitely.
Tests of Divisibility
- Division by 2: A number is divisible by 2 if its last digit is even. For example, 52 is divisible by 2 because its last digit, 2, is even.
- Division by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. For instance, 192 is divisible by 3 because the sum of its digits (1 + 9 + 2 = 12) is divisible by 3.
- Division by 4: A number is divisible by 4 if its last two digits form a number that is divisible by 4. For example, 172 is divisible by 4 because the last two digits, 72, are divisible by 4.
- Division by 5: A number is divisible by 5 if its last digit is either 0 or 5. For instance, 65 and 90 are divisible by 5 because their last digits are 5 and 0, respectively.
- Division by 10: A number is divisible by 10 if its last digit is 0. For example, 1120 is divisible by 10 because its last digit is 0.
- Even Natural Numbers (E): These are natural numbers that are divisible by 2. The set of even natural numbers is E = {2, 4, 6, 8, 10, 12, 14, ...}
- Odd Natural Numbers (O): These are natural numbers that are not divisible by 2. The set of odd natural numbers is O = {1, 3, 5, 7, 9, ...}.
- Prime Natural Numbers (P): A prime number is a natural number greater than 1 that is divisible only by itself and 1. The set of prime natural numbers is P = {2, 3, 5, 7, 11, ...}.
Estimation
- Estimation is a method to find an approximate value of a number or calculation. It helps us get a rough idea quickly, especially when exact calculations are not needed.
- Estimation is useful for checking results in addition, subtraction, multiplication, and division.
- For example, if you have 47 apples, you might estimate it as 50 to make calculations easier.
Rounding Off Numbers
Rounding off is a way to simplify numbers by making them easier to work with. The rules depend on the place value you are rounding to.
General Rounding Rules:
- If the digit to the right of the place you are rounding to is 5 or more, round up (add 1 to the place value).
- If the digit is less than 5, round down (keep the place value the same).
Rounding Examples:
Example: Round 6,789 to different place values:
- To the nearest ten: 6,789 → 6,790 (since 9 is greater than 5)
- To the nearest hundred: 6,789 → 6,800 (since 8 is greater than 5)
- To the nearest thousand: 6,789 → 7,000 (since 7 is greater than 5)
Estimation in Multiplication
For multiplication, round off each number to its greatest place value, then multiply the rounded numbers to get an estimate.
Example: Estimate 47 × 23
- Round 47 to 50 (nearest ten).
- Round 23 to 20 (nearest ten).
- Multiply: 50 × 20 = 1,000
- So, 47 × 23 is approximately 1,000.
Roman Numerals
- Roman numerals are a number system used in ancient Rome, represented by letters like I, V, X, L, C, D, and M.
- They are sometimes used in clocks, book chapters, or outlines.
Basic Roman Numerals:
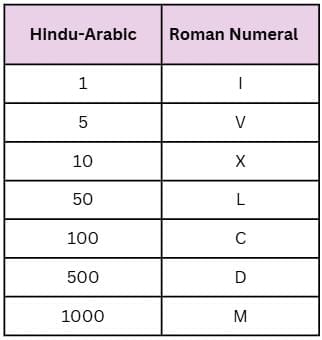
Rules for Roman Numerals:
- A symbol is not repeated more than three times (e.g., III is valid, but IIII is not).
- Symbols V, L, and D are never repeated.
- If a smaller value symbol is to the right of a larger value symbol, add the values (e.g., VI = 5 + 1 = 6, XII = 10 + 2 = 12).
- If a smaller value symbol is to the left of a larger value symbol, subtract it (e.g., IV = 5 - 1 = 4, XL = 50 - 10 = 40).
- Symbols V, L, and D are never subtracted.
- I can only be subtracted from V or X (e.g., IV = 4, IX = 9).
- X can only be subtracted from L or C (e.g., XL = 40, XC = 90).
Example: Convert the following to Hindu-Arabic numbers:
- VI = 5 + 1 = 6
- XII = 10 + 2 = 12
- LXV = 50 + 10 + 5 = 65
- IV = 5 - 1 = 4
- XC = 100 - 10 = 90
Metric System Conversions
The metric system is used to measure length, mass, and capacity. Common prefixes indicate how much larger or smaller a unit is compared to a base unit.
Common Prefixes:
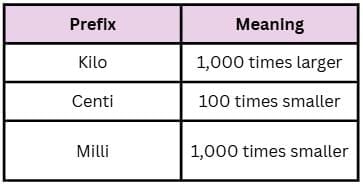
Metric Conversions:
- 1 kilometre = 1,000 metres
- 1 metre = 100 centimetres
- 1 metre = 1,000 millimetres
- 1 centimetre = 10 millimetres
Example: Convert 2.5 kilometres to metres.
Ans: 2.5 km × 1,000 = 2,500 metres
|
44 videos|201 docs|24 tests
|
FAQs on Revision Notes: Number System - Mathematics Class 6 ICSE
| 1. What is a number system? |  |
| 2. What are natural numbers and whole numbers? |  |
| 3. How do integers differ from whole numbers? |  |
| 4. What are rational and irrational numbers? |  |
| 5. Why is the number system important in mathematics? |  |















