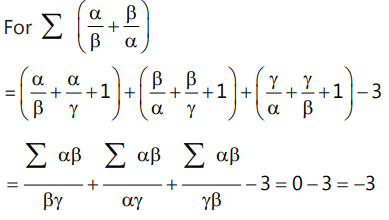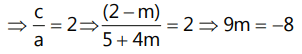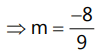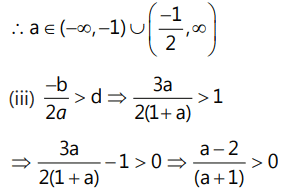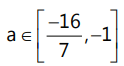Revision Notes: Quadratic Equations | Mathematics (Maths) for JEE Main & Advanced PDF Download

Important Formulas
(a) A quadratic equation is represented as:
ax2 + bx + c= 0, a ≠ 0
(b) Roots of quadratic equation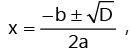 where D(discriminant) = b2 − 4ac
where D(discriminant) = b2 − 4ac
(c) Nature of roots
(i) D > 0 ⇒ roots are real and distinct (unequal)
(ii) D = 0 ⇒ roots are real and equal (coincident)
(iii) D < 0 ⇒ roots are imaginary and unequal
(d) The roots ( α+ iβ ) , ( α− iβ ) and ( α+ β ) , ( α− β ) are the conjugate pair of each other.
(e) Sum and Product of roots :
If α andβ are the roots of a quadratic equation, then
(i)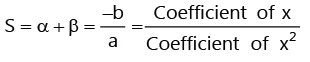 (ii)
(ii)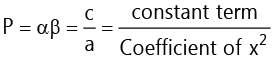
(f) Equation in the form of roots: x2 − ( α +β ) x + ( α. β ) = 0
(g) In equation ax2 + bx + c= 0, a ≠ 0 If
(i) b = 0 ⇒ roots are of equal magnitude but of opposite sign.
(ii) c = 0 ⇒ one root is zero and other is –b/a
(iii) b = c = 0 ⇒ both roots are zero.
(iv) a = c ⇒ roots are reciprocal to each other.
(v) a > 0, c < 0 or a < 0, c > 0 ⇒ roots are of opposite signs.
(vi) a > 0, b > 0, c > 0 or a < 0, b < 0, c < 0 ⇒ both roots are –ve.
(vii) a > 0, b < 0, c > 0 or a < 0,b > 0, c < 0 ⇒ both roots are +ve.
(h) The equations a1 x2 + b1 x + c1= 0 and a2x2 + b2 x + c2 = 0 have
(i) One common root if 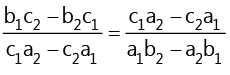 (ii) Both roots common if
(ii) Both roots common if 
(i) In equation ax2 + bx + c = a 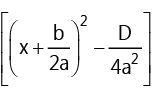
(i) If a>0, the equation has minimum value = 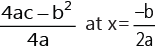 and there is no maximum value.
and there is no maximum value.
(ii) If a < 0, the equation has maximum value 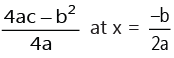 and there is no minimum value.
and there is no minimum value.
(j) For cubic equation ax3 + bx2 + cx + d = 0 ,
(i) 
(ii)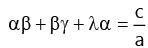
(iii) 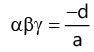 … where α ,β, γ are its roots.
… where α ,β, γ are its roots.
Solved Examples
Que1: Determine the values of m for which the equations 3x² + 4mx + 2 = 0 and 2x² + 3x - 2 = 0 may have a common root.
Ans:
The given equations are:
3x² + 4mx + 2 = 0
2x² + 3x - 2 = 0
Let the common root be a.
Substituting a into both equations:
For the first equation:
3a² + 4ma + 2 = 0
For the second equation:
2a² + 3a - 2 = 0
Solving the second equation:
2a² + 3a - 2 = 0
(2a - 1)(a + 2) = 0
Thus, the possible values of a are:
a = 1/2 or a = -2Case 1: If a = 1/2, substitute into the first equation:
3(1/2)² + 4m(1/2) + 2 = 0
3(1/4) + 2m + 2 = 0
3/4 + 2m + 2 = 0
2m + 11/4 = 0
2m = -11/4
m = -11/8
Case 2: If a = -2, substitute into the first equation:
3(-2)² + 4m(-2) + 2 = 0
3(4) - 8m + 2 = 0
12 - 8m + 2 = 0
14 - 8m = 0
8m = 14
m = 7/4
Final Answer: The values of m are:
m = -11/8 or m = 7/4
Que2: Solve for x when
log₁₀(√(log₁₀x)) = log₁₀(x²), x : x > 1
Ans:
By using the formulas:
logₐ(Mˣ) = x · logₐ(M) and logᵦ(a) = log₁₀(a) / log₁₀(b),
we can solve this problem.
log₁₀(√(log₁₀x)) = log₁₀(x²)
√(log₁₀x) = log₁₀x / log₁₀(x²) = 1/2
Let y = log₁₀x; then
1/2 = log₁₀(√y)
⇒ 1/2 = 1/2 log₁₀(y) ∴ y = 10
Thus,
x = 10ʸ = 10¹⁰
Que3: If the equations
x² + 2x + 3 = 0 and ax² + bx + c = 0, a, b, c ∈ ℝ,
have a common root, then a : b : c is:
(A) 1 : 2 : 3
(B) 3 : 2 : 1
(C) 1 : 3 : 2
(D) 3 : 1 : 2
Ans:
The first equation is:
x² + 2x + 3 = 0
The second equation is:
ax² + bx + c = 0
Since the two equations have a common root, the coefficients of the two equations are proportional.
Comparing coefficients, we get:
a : b : c = 1 : 2 : 3
Final Answer:
(A) 1 : 2 : 3
Que4: The equation
√(x + 1) - √(x - 1) = √(4x - 1) has:
(A) No solution
(B) One solution
(C) Two solutions
(D) More than two solutions
Ans:
Given:
√(x + 1) - √(x - 1) = √(4x - 1)
Squaring both sides:
(√(x + 1) + √(x - 1)) - 2√(x² - 1) = √(4x - 1)
Simplify:
1 - 2x = 2√(x² - 1)
1 + 4x² - 4x = 4x² - 4
Solve forx
4x = 5
x = 5/4
However, x=5/4 does not satisfy the original equation.
Conclusion: No solution exists.
Final Answer: (A) No solution
Que5: Let ‘a’ be a real number. Number of real roots of the equation
(x² + ax + 1)(3x² + ax − 3) = 0 is
(A) At least two
(B) At most two
(C) Exactly two
(D) All four
Ans:
(A) (x² + ax + 1)(3x² + ax − 3) = 0
D₁ = a² − 4
D₂ = a² + 36
D₂ is always > 0.
∴ The equation has at least two real roots.
Que6: If x be the real number such that x³ + 4x = 8, then the value of the expression x⁷ + 64x² is
(A) 124
(B) 125
(C) 128
(D) 132
Ans:
Sol 13: (C) (x³ + 4x)² = 82
⇒ x⁶ + 16x² + 8x⁴ = 64;
Multiply both sides by x:
⇒ x⁷ + 16x³ + 8x⁵ = 64;
Add 16x³ in both sides:
⇒ x⁷ + 8x⁵ + 32x³ = 16x³ + 64;
⇒ x⁷ + 8x³(x² + 4x) = 16(x³ + 4x);
⇒ x⁷ + 8x² × 8 = 16 × 8;
⇒ x⁷ + 64x² = 128.
Que7: If a, b, c are real numbers satisfying the condition a + b + c = 0, then the roots of the quadratic equation3ax² + 5bx + 7c = 0 are:
(A) Positive
(B) Real & distinct
(C) Negative
(D) Imaginary
Ans: (d)
D of equation = 25b² - 84ac = 25(a + c)² - 84ac
= -34ac + 25c² + 25a²Since D < 0, the roots are always imaginary when a ≠ 0.
Thus, the correct answer is (D) Imaginary.
Que8: If the roots of 2x³ + x² − 7 = 0 are α, β and
f(x) = x² + x(4 − 2k) + k² − 3k − 1 = 0,
find the value of ∑(α/β + β/α).
Ans: Given that, 2x³ + x² − 7 = 0
For roots, α + β + γ = −1/2, αβ + βγ + γα = 0, and αβγ = −7/2
Que9: Find the value of m, for which the equation
5x² − 4x + 2 + m(4x² − 2x − 1) = 0 has
(i) Equal roots
(ii) Product of the roots as 2
Ans:
The equation is 5x² − 4x + 2 + m(4x² − 2x − 1) = 0
⇒ (5 + 4m)x² − (4 + 2m)x + (2 − m) = 0
(i) If the equation has equal roots, then b² − 4ac = 0
⇒ [−(4 + 2m)]² − 4(5 + 4m)(2 − m) = 0
⇒ 4m² + 16m + 16 − 4(4m² + 3m + 10) = 0
⇒ 20m² + 4m − 24 = 0
⇒ 5m² + m − 6 = 0
⇒ (m − 1)(5m + 6) = 0
⇒ m = 1 or m = −6/5
(ii) Product of roots is 2:
Que10: Find all the values of a for which the roots of the equation (1 + a)x² − 3ax + 4a = 0 exceed unity.
Ans:
15: (1 + a)x² − 3ax + 4a = 0
Let f(x) = (a + 1)x² − 3ax + 4a and d = 1.
The roots exceed unity:The conditions are:
(i) D ≥ 0
(ii) 9a² − 16a(1 + a) ≥ 0
⇒ 9a² − 16a − 16a² ≥ 0
⇒ 7a² + 16a ≤ 0(ii) a f(d) > 0
Note that this a is the coefficient of x² and not to be confused with 'a'
⇒ (1 + a)(1 + a − 3a + 4a) > 0
⇒ (1 + a)(2a + 1) > 0∴ a ∈ (-∞, -1) ∪ (2, ∞)
So, taking the intersection of all three solutions:
|
172 videos|476 docs|154 tests
|
FAQs on Revision Notes: Quadratic Equations - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the different methods to solve quadratic equations? |  |
| 2. How do I determine the nature of the roots of a quadratic equation? |  |
| 3. What is the significance of the vertex in a quadratic equation? |  |
| 4. Can quadratic equations have complex roots, and how do we find them? |  |
| 5. How can I apply the quadratic equation to solve real-world problems? |  |