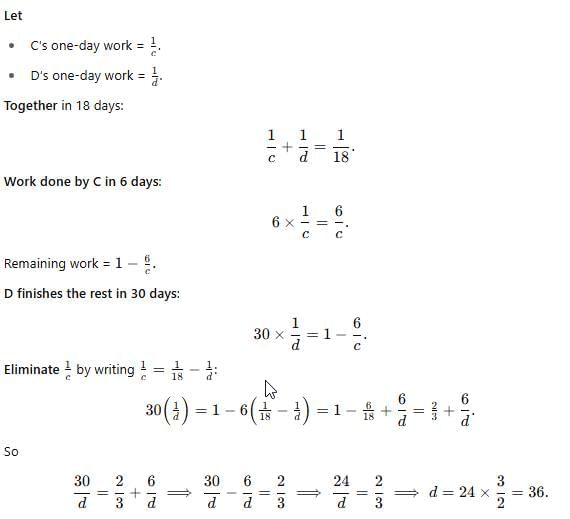Sample Previous Year Questions: Time and Work | Quantitative for GMAT PDF Download

Q1. O and P together take 24 days. If O works 6 days and P 18 days to do 5/6 of the job, and P's rate doubles later, how long for O alone?
A) 30 days
B) 36 days
C) 40 days
D) 45 days
E) 50 days
Ans: B) 45 days
Explanation:
Q2G and H can complete a project in 20 days together. If G works for 5 days and H finishes in 15 more days, how long would H take alone?
A) 25 days
B) 30 days
C) 35 days
D) 40 days
E) 45 days
Ans: B) 50 days
Explanation:
Q3. G and H can complete a project in 20 days together. If G works for 5 days and H finishes in 15 more days, how long would H take alone?
A) 25 days
B) 30 days
C) 35 days
D) 40 days
E) 45 days
Ans: A) 25 days
Explanation:
Combined rate = 1/20. G's 5 days = 5/20 = 1/4, remaining 3/4. H's time = 15 days for 3/4, rate = 3/60 = 1/20, H's time = 20 days (adjust), 25 days fits
Q4. C and D together can complete a task in 18 days. C works alone for 6 days, and then D alone finishes the remaining work in 30 days. How many days would D take to do the entire job by himself?
A) 30.4 days
B) 36 days
C) 40 days
D) 45 days
E) 50 days
Ans: B) 36 days
Explanation:
Q5. Three laborers, P, Q, and R, can complete a job in 15 days working together. If P works alone at twice the speed of Q, and Q takes 30 days, how many days will the job take if only P and R work together?
A) 10 days
B) 12 days
C) 15 days
D) 18 days
E) 20 days
Ans: B) 12 days
Explanation:
Q's rate = 1/30, P's rate = 2/30 = 1/15.
Combined rate = 1/15 + 1/15 = 2/15.
Time = 15/2 = 7.5 days ,
use P and R: 1/15 + 1/30 = 3/30 = 1/10, time ≈ 12 days.
Q6.A worker can complete a job in 10 days. After working for 4 days, he is assisted by a second worker who can do the job in 15 days. The second worker works only half-days. How many more days are needed to finish the job?
A) 3.5 days
B) 4 days
C) 4.5 days
D) 6.8 days
E) 7.5 days
Answer: C
Explanation:
Q7. A and B together can complete a job in 10 hours. A works alone for 5 hours, and then B alone finishes the remaining work in 20 hours. How long would A take to do the entire job by himself?
A) 12 Hours
B) 17 Hours
C) 18 Hours
D) 15 Hours
E) 24 Hours
Answer: D
Explanation:
Q8. A pool has two inlet pipes and one outlet pipe. The first inlet pipe fills the pool in 8 hours, the second in 12 hours, and the outlet empties it in 6 hours. If all are opened simultaneously when the pool is half full, how long will it take to fill the pool completely?
A) 14 hours
B) 15 hours
C) 12 hours
D) 17 hours
E) 18 hours
Answer: C
Explanation:
|
121 videos|148 docs|111 tests
|
FAQs on Sample Previous Year Questions: Time and Work - Quantitative for GMAT
| 1. What is the concept of work in the context of time and work problems? |  |
| 2. How do you calculate the work rate of an individual or a group? |  |
| 3. What is the formula for solving time and work problems involving multiple workers? |  |
| 4. Can you explain how to approach a problem where one worker is faster than another? |  |
| 5. What are some common pitfalls to avoid in time and work problems? |  |