Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 1 | Mathematics (Maths) Class 10 PDF Download
Class X
Mathematics – Standard (041)
Sample Question Paper 2019-20
Max. Marks: 80
Duration : 3 hrs
General Instructions:
(i) All the questions are compulsory.
(ii) The question paper consists of 40 questions divided into 4 sections A, B, C, and D.
(iii) Section A comprises of 20 questions of 1 mark each. Section B comprises of 6 questions of 2 marks each. Section C comprises of 8 questions of 3 marks each. Section D comprises of 6 questions of 4 marks each.
(iv) There is no overall choice. However, an internal choice has been provided in two questions of 1 mark each, two questions of 2 marks each, three questions of 3 marks each, and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
(v) Use of calculators is not permitted.
Section A
Q.1. If the sum of the roots of the quadratic equation ax2 - 5x + 11 = 0 is 15, then the value of a is : (1 Mark)
(a) 11/15
(b) 3
(c) 15/11
(d) 1/3
Ans. (d)
Solution.
Given, sum of the roots = 15
⇒ - (-5)/a = 15 [∵ Sum of roots = - Coeff. of x / Coeff. of x2]
⇒ a = 5/15 = 1/3
Q.2. The zeroes of the polynomial 21y2 - 11y - 2 = 0 are (1 Mark)
(a) -2/7 , 1/3
(b) -2/3, -1/7
(c) 2/3, -1/7
(d) -2/3, 1/7
Ans. (c)
Solution.
Given, 21y2 - 11y - 2 = 0 ⇒ 21y2 - 14y + 3y - 2 = 0
⇒ 7y (3y - 2) + (3y - 2) = 0 ⇒ (3y - 2) (7y + 1) = 0
⇒ y = 2/3 or y = -1/7
Q.3. The LCM of smallest two digit composite number and smallest composite number is: (1 Mark)
(a) 12
(b) 4
(c) 20
(d) 44
Ans. (c)
Solution.
[Here, the smallest two digit composite number = 10 The smallest composite number = 4 Now, LCM of 4 and 10 = 20]
Q.4. The 21st term of the A.P, whose first two terms are -3 and 4 is : (1 Mark)
(a) 17
(b) 137
(c) 143
(d) -143
Ans. (b)
Solution.
In the given A.P, t1 = -3 and t2 = 4
⇒ d = t2 - t1 = 4 - (-3) = 7
tn = a + (n - 1) d
⇒ f21 = (-3) + (21-1)(7) = 137
Q.5. In figure, DE||BC, AD = 1 cm and BD = 2 cm. Then ar(ΔABC) : ar(ΔADE) = ? (1 Mark)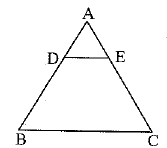
(a) 2 : 1
(b) 9 : 1
(c) 3 : 1
(d) 1 : 9
Ans. (b)
Solution.
Given, DE||BC, so that ΔABC ~ ΔADE
Given, AD = 1 cm and BD = 2 cm, so that AB = AD + BD = 1 cm + 2 cm = 3 cm.
The ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
∴ ar (ΔABC)/ar (ΔADE) = AB2/AD2 = (AB/AD)2 = (3/1)2 = 9/1 or 9 : 1
Q.6. Two coins are tossed simultaneously. What is the probability of getting tails on both the coins ? (1 Mark)
(a) 1/4
(b) 1/3
(c) 3/8
(d) 1/2
Ans. (a)
Solution.
Total possible outcomes
= (H, H), (H, T), (T, H), (T,T)
E = Event of getting tails on both the coins.
= (T, T)
∴ P(E) = 1/4
Q.7. Given that sin α = √3/2 and cos β = 0, then the value of β - a is: (1 Mark)
(a) 0°
(b) 90°
(c) 60°
(d) 30°
Ans. (d)
Solution.
[sin α = √3/2 ⇒ α = 600 and cos β = 0
Now, β - α = 900 - 600 = 300]
Q.8. If cos (α + β) = 0, then sin (α - β) can be reduced to (1 Mark)
(a) cos β
(b) cos 2β
(c) sin α
(d) sin 2α
Ans. (b)
Solution.
cos (α + β) = 0
cos(α + β) = cos 90°
α + β = 90°
α = 90° - β
sin (α - β) = sin (90° - β - β)
= sin (90° - 2β)
= cos 2β
Q.9. If tan 2A = cot (A - 24°), then A = ___. (1 Mark)
Ans. 38°
Given tan 2A = cot (A - 24°)
⇒ cot (90° - 2A) = cot (A - 24°) [∵ tan θ = cot (90° - θ)]
⇒ 90° - 24 = A - 24°
⇒ 90° + 24° = A + 2A
⇒ 3A - 114°
⇒ A = 38°
Q.10. Median class is the class whose cumulative frequency is (1 Mark)
(a) less than n/2
(b) greather than n/2
(c) less than n/4
(d) greater than n/4
Ans. (b)
Solution.
Median class is the class whose cumulative frequency is greater than n/2.
Q.11. The total surface area of the given solid figure is _______. (1 Mark)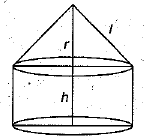
Ans. πr2 + 2πrh + πrl
[i.e., surface area of base + C.S.A. of cylinder + C.S.A. of cone]
Q.12. If the zeroes of the quadratic polynomial x2 + (a + 1) x + b are 2 and -3, then find the value of a and b. (1 Mark)
Ans. Let f(x) = x2 + (a + 1)x + b
As 2, and (-3) are zeroes of polynomial
f(x) = x2 + (a + 1)x + b, then
f(2) = 0
(2)2 + (a + 1)(2) + b = 0
4 + 2a + 2 + b = 0
2a + b = -6 ......(i)
And f(-3) = 0
(3)2+(a + 1)(-3) + b = 0
9 - 3a - 3 + b = 0
-3a + b = -6
3a-b = 6 ..... (ii)
5a = 0 [Adding (i) and (ii)]
a = 0
But 2a + b = - 6 [From (i)]
2(0) + b = - 6
⇒ b = - 6
Hence, the value of a = 0 and b = - 6.
Q.13. The following questions consist of two statements - Assertion (A) and Reason (R). Answer these questions selecting the appropriate option given below : (1 Mark)
(a) Both A and R are true and R is the correct explanation for A.
(b) Both A and R are true and R is not the correct explanation for A.
(c) A is true but R is false.
(d) A is false but R is true.
Assertion (A) : In a circle of radius 6 cm, the angle of sector is 60°. Then the area of sector is (18)6/7 cm2.
Reason (R) : Area of thee circle with radius r is πr2.
Ans. (b)
Solution.
Area of the sector = θ/360º × πr2 = 60º/360° × 22/7 × 6 × 6 = 132/7 = (18)6/7 cm2.
Q.14. The line joining the observer's eye and the object is called the _______. (1 Mark)
Ans. Line of sight
Q.15. A number is chosen at random from the numbers - 5, - 4, - 3, - 2, - 1, 0, 1 , 2, 3, 4, 5. Then the probability that square of this number is less than or equal to 1 is (1 Mark)
Ans. 3/11 [∵ The required numbers are - 1, 0,1. Hence, the probability = 3/11]
Q.16. In the given figure,, if ∠A = 90°, ∠B = 90°, OB = 4.5 cm, OA = 6 cm and AP = 4 cm, then find QB. (1 Mark)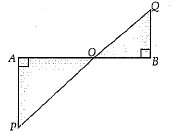
Ans. In ΔPAO and ΔQBO,
∠A = ∠B = 90° (Given)
∠POA = ∠QOB
(Vertically Opposite Angle)
Since, ΔPAO ~ ΔQBO,
(by AA)
Then, OA/OB = PA/QB
Or 6/4.5 = 4/QB
Or QB = 4 × 4.5 / 6
∴ QB = 3 cm
Q.17. Write the condition for unique solution of a system of linear equations a1x + b1y + c1 = 0 Q and a2x + b2y + c2 = 0. (1 Mark)
Ans. The system of given linear equations has a unique solution if
a1/a2 ≠ b1/b2
Q.18. The graph of y = p(x) is given below, find the number of zeroes of p(x). (1 Mark)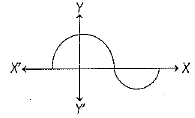
Ans. It is clear from the graph that curve intersects the X-axis at three points.
Hence, number of zeroes of the polynomial y = p(x) are three.
Q.19. If the first three terms of an AP are b, c and 2b, then find the ratio of b and c.(1 Mark)
Ans. Here, b, c, 2b are in AP
∴ c - b = 2b - c
⇒ 3b = 2c
⇒ b/c = 2/3
Hence, b : c = 2: 3.
Q.20. A die is thrown once. Find the probability of getting "at most 2." (1 Mark)
Ans. S = {1, 2, 3, 4, 5, 6}
n(S) = 6
A = {1,2}
n(A) = 2
∴ P(A) = n(A)/n(S) = 2/6 = 1/3
Section B
Q.21. Find the HCF of 1260 and 7344 using Euclid’s algorithm.
Or
Show that every positive odd integer is of the form (4q + 1) or (4q + 3), where q is some integer. (2 Mark)
Ans. Given integers are 1260 and 7344. Clearly 7344 > 1260.
Applying Euclid’s division algorithm, we get
7344 = 1260 × 5 + 1044
1260 = 1044 × 1 + 216
1044 = 216 × 4 + 180
216 = 180 × 1 + 36
180 = 36 × 5 + 0
In the last equation, the remainder is zero and divisor in the last equation is 36.
Hence, HCF of 1260 and 7344 = 36.
Or
Let a be any odd positive integer.
When a is divided by 4, remainder will be one of 0, 1, 2, 3.
∴ a = 4q + 0 i.e., 4q or 4q + 1 or 4q + 2 or 4q + 3
When a = 4q, which is even positive integer as it is divisible by 2.
When a = 4q + 2 = 2(2q + 1), which is even positive integer as it is divisible by 2.
Hence, every odd positive integer is of the form 4q + 1 or 4q + 3.
Q.22. Read the following passage and answer the questions that follows:
A teacher of Xth class draw a figure on blackboard and asked one question about figure from students that, if ΔACB ~ ΔAPQ, AB = 6 cm, BC = 8 cm and PQ = 4 cm, then find the length of AQ. (2 Mark)
Ans. As ΔACB ~ ΔAPQ
So, AB/BC = AQ/QP ⇒ 6/8 = AQ/4
[∵ AB = 6 cm, BC = 8 cm and PQ = 4 cm, given]
⇒ 6 x 4 / 8 = AQ = 3cm
Q.23. In the given figure, DEFG is a square and ∠BAC = 90°. Show that FG2 = BG x FC. (2 Mark)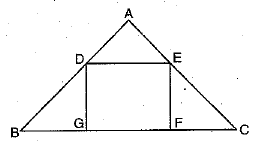
Or
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Ans. In ΔADE and ΔGBD
∠A = ∠G = 90°
∠ADE = ∠DBG
[corresponding ∠s]
∴ By using AA similarity rule, we have
ΔADE ∼ ΔGBD
Similarly, ΔADE ∼ ΔFEC
⇒ ΔGBD ∼ ΔFEC
[AA similarity criterion]
∴ GD/FC = GB/FE
⇒ GD × FE = GB × FC
⇒ FG × FG = BG × FC
[∵ GD = FE = DE = FG, as DEFG is a square]
⇒ FG2 = BG × FC
Or
In an equilateral ΔABC, draw AD ⊥ BC.
∴ AD is also the median
i.e., BD = DC = BC/2 .
Now, in rt. ∠ed ΔABD
AB2 = AD2 + BD2
= AD2 + (BC/2)2
= AD2 + BC2/4
4AB2 = 4AD2 + BC2
4AB2 - BC2 = 4AD2
4AB2 - AB2 = 4AD2
3AB2 = 4AD2
[∵ AB = BC = CA]
Q.24. If the point P(x, y) is equidistant from the points Q (a + b , b - a ) and R(a - b , a + b), then prove that bx = ay. (2 Mark)
Ans.
|PQ| = |PR|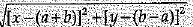
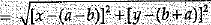
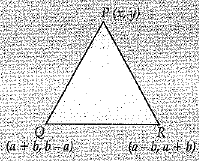
Squaring, we get
[x - (a + b)]2 + [y - (b - a)]2
= (x - (a - b)]2 + [y - (a + b)]2
or (x - a - b)2 [x - a + b]2
= (y - a - b)2 - (y - b + a)2
or, (x - a - b + x - a + b) (x - a - b - x + a - b)
= (y - a - b + y - b + a) (y - a - b - y + b - a)
or (2x - 2a) (-2b) = (2y - 2b) (-2a)
or, (x - a) = (y - b)a
or, bx = ay
Q.25. A die is thrown once. Find the probability of getting a number which (i) is a prime number (ii) lies between 2 and 6. (2 Mark)
Ans. When a die is thrown once, the possible outcomes are 1, 2, 3, 4, 5 and 6.
Total number of all possible outcomes = 6
Let A and B be events of getting a prime number and a number lying between 2 and 6.
(i) Prime numbers are 2, 3 and 5, so number of cases in favour of event A = 3
Probability of getting a prime number = P(A)
= Number of cases in favour of event A/Total number of cases = 3/6 = 1/2
(ii) Numbers lying between 2 and 6 are 3, 4 and 5.
∴ Number of cases in favour of event B = 3
Probability of getting a number that lies between 2 and 6
= P(B) = Number of cases in favour of event B/Total number of cases = 3/6 = 1/2
Q.26. Express 234 as the product of its prime factors.
Or
Show that any positive odd integer is of the form 4q +1 or 4q + 3, where q is a positive integer. (2 Mark)
Ans. We have,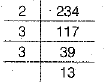
∴ 234 = 2 × 3 × 3 × 13
Or
Let a be any positive odd integer and b = 4.
By Euclid’s division algorithm, there exists integers ^ and r such that
a = 4q + r, where 0 < r < 4
a = 4q or 4g + 1 or 4q + 2 or 4g + 3
[∵ r = 0,1,2, 3]
⇒ a = 4g + 1 or a = 4q + 3
[∵ a is an odd integer ⇒ and a ≠ 4q + 2]
Hence, any odd integer is of the form 4q +1 or 4q + 3.
Section C
Q.27. Prove that √2 is an irrational number.
(3 Mark)
Ans. Let us assume to the contrary that √2 is a rational number. Then, there exists positive integers a and b such that
√2 = a/b, where a and b are coprime i.e., their HCF is 1 and b ≠ 0.
⇒√2b = a
Squaring both sides, we get
2b2 - a2
⇒ 2 divides a2
⇒ 2 divides a ......(1)
[If a prime number r divides a2, then prime number r divides a]
∴ a = 2m, for some integer m
Substituting a = 2m in 2b2 = a2, we have
2b2 = (2m)2 ⇒ b2 = 2m2
⇒ 2 divides b2
⇒ 2 divides b
From (1) and (2), we find that a and b have at least 2 as a common factor. But, this contradicts the fact that a and b are coprime. This contradiction has arisen because of our incorrect assumption that √2 is a rational number.
Q.28. The following table shows the age distribution of cases of a certain disease admitted during a year in a particular hospital.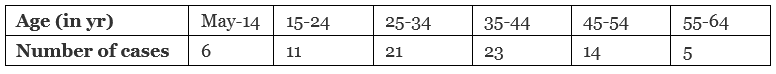
Find the average age for which maximum cases occurred. (3 Mark)
Ans.
Here, class intervals are not in inclusive form.
So, we first convert them in inclusive form by subtracting h/2 from the lower limit and adding h/2 to the upper limit of each class, where h is the difference between the lower limit of a class and the upper limit of the preceding class.
The given frequency distribution in inclusive form is as follows:
We observe that the class 34.5-44.5 has the maximum frequency.
So, it is the modal class such that
I = 34.5, h = 10, f = 23, f1 = 21 and f2 = 14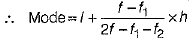
Q.29. In the figure, ABCDE is a pentagon with BE||CD and BC||DE. BC is perpendicular to CD. AB = 5 cm, AE = 5 cm, BE = 7 cm, BC = x - y and CD = x + y. If the perimeter of ABCDE is 27 cm, find the value of x and y, given x, y ≠ 0. (3 Mark)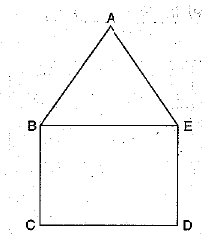
Or
Solve the following system of equations:
21/x + 47/y = 100
47/x + 21/y = 162, x, y ≠ 0
Ans. Here, AB = AE = 5 cm, BE = 7 cm,
BC = x - y and CD = x + y.
∴ x + y = 7 ...(i)
And BC + CD + DE + AE + AB = 27
∴ x - y + x + y + x - y + 5 + 5 = 27
∴ 3x - y = 17 ...(ii)
Adding (i) and (ii), we obtain
4x = 24
⇒ x = 6
From (i), we obtain 6 + y = 7 ⇒ y = 1
Hence, x = 6 and y = 1.
Or
Given equations are
21/x + 47/y = 110
47/x + 21/y = 162
Put 1/x = a and 1/y = b.
21a + 47b = 110 ......(i)
47a + 21b = 162 ......(ii)
Adding (i) and (ii), we obtain
68a + 68b = 272
a + b = 4 ......(iii)
Subtracting (i) and (ii), we obtain
26a - 26b = 52
a - b = 2 ...........(iv)
Adding (iii) and (iv) we have
2a = 6 ⇒ a = 3
From (iii), we have
3 + b = 4 b = 1
Now, a =1/x = 3 ⇒ x = 1/3
and, b = 1/y = 1 ⇒ y = 1
Q.30. Prove that:
cot θ - tan θ = 2cos2θ - 1/sinθcosθ (3 Mark)
Ans. LHS = cotθ - tanθ
= cosθ/sinθ - sinθ/cosθ
= cos2θ - sin2θ/sinθcosθ
= cos2θ - 1 + cos2θ/sinθcosθ
= 2cos2θ - 1/sinθ cosθ = RHS
Q.31. Prove that:
(sin θ + cosec θ)2 + (cos θ + sec θ)2 = 7 + tan2 θ + cot2 θ.
Or
Prove that:
(1 + cot A - cosec A)(1 + tan A + sec A) = 2. (3 Mark)
Ans. We have
L.H.S. = (sin θ + cosec θ)2 + (cos θ + sec θ)2
= sin2 θ + cosec2 θ + 2 sin θ cosec θ + cos2 θ + sec2 θ + 2 cos θ sec θ
= (sin2 θ + cos2 θ) + cosec2 θ + sec2 θ + 2 sin θ.cosec θ + 2 cos θ.sec θ
= (sin2θ+ cos2θ) + (1 + cot2θ) + (1+tan2θ) + 2sinθ. 1/sinθ + 2 cosθ. 1/cosθ
= 1 + (1 + cot2θ) + (1 + tan2θ) + 2 + 2
= 7 + tan2θ + cot2θ
= R.H.S.
Or
We have
L.H.S = (1 + cot A - cosec A) (1 + tan A + sec A)
= (1 + cos A/ sin A - 1 / sin A)(1 + sin A/cos A + 1/cos A)
= (sin A + cos A - 1 / sin A) (cos A + sin A + 1 / cos A)
= (sin A + cos A)2 - 1 / sin A cos A = sin2 A + cos2 A + 2 sin A cos A - 1 / sin A cos A
= (sin2A + cos2A) + 2 sin A cos A - 1 /sin A cos A = 1 + 2 sin A cos A - 1 / sin A cos A
= 2 sin A cos A / sin A cos A = 2
= R. H. S.
Q.32. The Resident Welfare Association of a , colony decided to build two straight paths in their neighbourhood park such that they do not cross each other, to plant trees along the boundary lines of each path.
One of the members of association, Sarika suggested that the paths should be constructed represented by the two linear equations x - 3y - 2 and - 2 x + 6y = 5.
Check whether the two paths will cross each other or not. (3 Mark)
Ans. Given linear equations are
x - 3y = 2
⇒ x - 3y - 2 = 0 ...(i)
and - 2x + 6y = 5
⇒ -2x + 6y - 5 = 0 ...(ii)
Here, a1 = 1, b1 = -3, c1 = -2
and a2 = -2, b2 = 6, c2 = -5
Now, a1/a2 = 1/-2 = - 1/2, b1/b2 = -3/6 = - 1/2
and c1/c2 = -2/-5 = 2/5
Here, a1/a2 = b1/b2 ≠c1/c2
So, the paths represented by the equations are parallel, i.e. not intersect each other.
Q.33. Sides of a right triangular field are 25 m, 24 m and 7 m. At the three comers of the field, a cow, a buffalo and a horse are tied separately with ropes of 3.5 m each to graze in the field. Find the area of the field that cannot be grazed by these animals. (3 Mark)
Ans.
Here, ar(ΔABC) = 1/2 × 24 × 7
= 84 m2 [∵ ∠A = 900]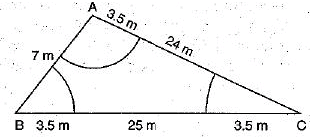
Area of three sectors = πr2 / 3600 × (1800)
= 1/2 x 22/7 × 3.5 × 3.5
= 77/4 = 19.25 m2
Required area = Area of ΔABC - Area of three sectors
= 84 - 19.25
= 64.75 m2.
Q.34. Use Euclid's Division Algorithm to find the HCF of 726 and 275. (3 Mark)
Ans. 726 = 275 × 2 +176
275 = 176 × 1 + 99
176 = 99 × 1 + 77
99 + 77 × 1 + 22
77 = 22 × 3 + 11
22 = 11 × 2 + 0
⇒ This HCF = 11
Section D
Q.35. Two water taps together can fill a tank in 15/8 hours. The tap with longer diameter takes 2 hours less than the tap with smaller one to fill the tank separately. Find the time in which each tap can fill the tank separately.
Or
A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water (4 Mark)
Ans. Let the time taken by the tap of smaller diameter = x hours
∴ Time taken by the tap of larger diameter
= (x - 2) hours
∴ Portion of the tank filled by the tap of smaller diameter in one hour = 1/x
and
Portion of the tank filled by the tap of larger diameter in one hour = 1/x-2
Thus, the portion of the tank filled by the two taps in one hour = 1/x + 1/x-2 ......(1)
It is given that both taps can fill the tank in = 15/8 hours
∴ The portion of the tank filled by the two taps in one hour = 8/15 .....(2)
From (1) and (2), we get
1/x - 1/x - 2 = 8/15
⇒ x - 2 + x / x(x - 2) = 8/15
⇒ 15(2x - 2) 8(x2 - 2x)
⇒ 8x2 - 16x - 30x + 30 = 0
⇒ 8x2 - 46x + 30 = 0
⇒ 4x2 - 23x + 15 = 0
⇒ 4x2 - 20x - 3x + 15 = 0
⇒ 4x(x - 5) - 3 (x - 5) = 0
⇒ (x - 5) (4x - 3) = 0
⇒ x - 5 = 0 or x = 3/4
When, x = 3/4, x - 2 = 3/4 - 2 = 3-8/4 = - 5/4, which is impossible as time to fill cannot be negative.
∴ When x = 5, x - 2 = 3
Hence, the larger pipe can fill the tank in 3 hours and the smaller pipe can fill the tank in 5 hour
Or
Let the speed of the boat in still water = x km/h
and the speed of the stream = y km/h
∴ Speed of the boat going upstream
= (x - y) km/h
and
Speed of the boat going downstream
= (x + y) km/h
We know that Time = Distance/Speed
∴ Time taken in going 30 km upstream
=(30/(x-y))h
and
Time taken in going 44 km downstream
= (44/(x+y))h
But, the total time of the journey is 10 hours.
∴ 30/x - y + 44/x+ y = 10 ....(1)
Again, Time taken in going 40 km upstream = (40/(x-y))h
and Time taken in going 55 km downstream = (55/(x+y))h
In this case, total time of journey is given to be 13 hours.
∴ 40/ x-y + 55/ x+y = 13 ...(2)
Multiplying (1) and (2) by 4 and 3 respectively, we pet
120/ x - y + 176 / x + y = 40 ...(3)
120/ x-y + 165/x+ y = 39 ......(4)
Subtracting (4) from (3), we get
11/ x + y = 1 ⇒ x + y = 11 ...(5)
Putting the value of x + y from (5) in (1), we have
30/x-y + 44/11 = 10 ⇒ 30/x - y = 6 ⇒ x - y = 5 ...(6)
Adding and subtracting (5) and (6), we get
2x = 16 and 2y = 6
⇒ a = 8 and y = 3
∴ Speed of the boat in still water = 8 km/h and speed of water stream = 3 km/h.
Q.36. The angles of a triangle are in AP. If the greatest angle equals to the sum of the other two, then find the angles. Also, find these angles are multiple of which angle.
Or
A sum of Rs. 1000 is invested at 8% simple interest per annum. Calculate the interest at the end of 1, 2, 3, ... years. Is the sequence of interests an AP? Find the interest at the end of 30 years. (4 Mark)
Ans. Let the angles of a triangle, are (a - d), a and (a + d).
Since, sum of the three angles of a triangle = 180°
∴ a - d + a + a + d = 180°
⇒ 3a = 180° ⇒ a = 60°
So, the angles are 60° - d , 60° and 60° + d .
According to the question,
Greatest angle = Sum of two smaller angles
∴ 60° + d = 60° - d + 60°
⇒ 2d = 60°
⇒ d = 30°
Hence, the required angles of a triangle are 60° - 30°, 60° and 60° + 30°, i.e. 30°, 60° and 90°.
Here, we see that above angles are multiple of 30°
Or
Sum of Rs. 1000 is invested at 8 % simple interest.
Interest at the end of 1st year
= 1000 x (8/100) × 1 = ₹ 80
Interest at the end of 2nd year
= 1000 x (8/100) × 2 = ₹ 160
Interest at the end of 3rd year
= 1000 x (8/100) × 3 = ₹ 240
Since, each interest is Rs. 80 more than the previous one.
Sequence of interest 80,160,240,... isanAR
Here, a = Rs. 80, n = 30
and d = a2 - a1 = Rs. (160 - 80) = Rs. 80
Now using an = a + (n - 1)d,
∴ a30 = 80 + (30 -1) (80)
⇒ a30 = 80 + (29) (80) = 80 + 2320 = 2400
Hence, interest at the end of 30 years is Rs. 2400
Q.37. A train covers a distance of 360 km at a uniform speed. Had the speed been 5 km/hour more, it would have taken 48 minutes less for the journey. Find the original speed of the train.
Or
Solve the following equation : (4 Mark)
Ans. Let the original speed of the train be x km/h. According to the statement of the question, we have
360/x - 360/x+5 = 48/60
360(x + 5 - x/x(x + 5)) = 4/5 (taking LCM of LHS)
360 x 5 x 5 = 4(x2 + 5x)
∴ x2 + 5x - 2250 = 0
⇒ (x + 50)(x - 45) = 0
∴ x = -50 or x = 45
Rejecting - ve value of x, because speed cann’t be negative, we have
x = 45
Hence, the original speed of the train is 45 km/h.
Or
1/x - 1/x-2 = 3
x-2-x/x(x-2) = 3
-2 = 3x2 - 6x
⇒ 3x2 - 6x + 2 = 0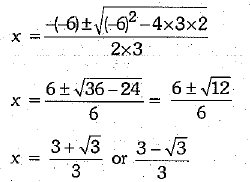
Q.38. Two poles of equal heights arc standing opposite to each other on either side of the road which is 80 m wide. From a point in between them on the road, the angles of elevation of the top of poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles.
OR
The angle of elevation of the top of a hill from the foot of a tower is 60° and the angle of depression from the top of the tower of the foot of the hill is 30°. If tower is 50 meter high, find the height of the hill. (4 Mark)
Ans.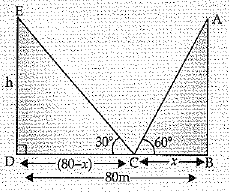
In ΔABC, h/x = tan 600
⇒ h = x√3 ...(1)
In ΔEDC, h/80-x = tan300
⇒ h√3 = 80 - x
From (1), x√3 × √3 = 80 - x
⇒ x = 20 m
∴ h = 20√3 m
∴ The height of poles = 20√3 m
Hence, the distance of poles from the point are 20 m and 60 m.
Q.39. Prove that in a right angled triangle, the square of the hypotenuse is equal the sum of squares of the other two sides. (4 Mark)
Ans. Given : A right triangle ABC, right angled at B.
To prove : (Hypotenuse)2 = (Base)2 + (Perpendicular)2
i.e., AC2 = AB2 + BC2 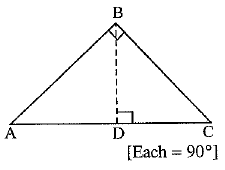
Construction : Draw BD ⊥ AC.
Proof : ΔADB ~ ΔABC.
In ΔADB and ΔABC
∠ADB = ∠ABC
and ∠A = ∠A
∴ By A A-similarity criterion, we have
ΔADB ~ ΔABC
So, AD/AB = AB/AC [In similar triangles, corresponding sides are proportional]
⇒ AD.AC = AB2 ......(1)
In ΔBDC and ΔASC
∠CDB = ∠ABC [Each= 90°]
and ∠C = ∠C
∴ ΔBDC ~ ΔABC
So, CD/BC = BC/AC [In similar triangles, corresponding sides are proportional]
⇒ CD.AC = BC2 ........(2)
Adding (1) and (2), we have
AD.AC + CD.A C = AB2 + BC2
⇒ (AD + CD) AC = AB2 + BC2
⇒ ACAC = AB2 + BC2
Hence, AC2 = AB2 + BC2
Q.40. Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle. (4 Mark)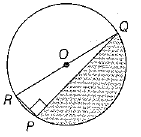
Ans. Given, PQ = 24 cm and PR = 7 cm
We know that any angle made by the diameter RQ in the semi-circle is 90°.
∴ ∠RPQ = 90°
In right angled ΔRPQ,
RQ2 = PR2 + PQ2 [by Pythagoras theorem]
⇒ RQ2 = 72 + 242 ⇒ RQ2 = 49 + 576
⇒ RQ2 = 625
⇒ RQ = √625 [∵ side cannot be negative]
⇒ RQ = 25 cm ...(1)
∴ Area of right angled ΔRPQ = 1/2 × RP × PQ
[∵ area of triangle - 1/2 × base × height]
= 1/2 × 7 × 24 = 84cm2
Area of semi-circle
= πr2/2 = (22/7 x 2)(25/2)2 [∵ = RQ/2 = 25/2 cm]
= 11 × 625 / 28 = 6875/28 cm2
Hence, area of the shaded region = Area of the semi-circle - Area of right angled ΔRPQ
= (6875/28) - (84)
= (6875 - 2352) / 28 (taking LCM)
= 4523 / 28 cm2
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 1 - Mathematics (Maths) Class 10
| 1. What is the importance of solving CBSE sample question papers for Class 10 Mathematics? |  |
| 2. How can solving CBSE sample question papers help in improving exam performance? |  |
| 3. Are CBSE sample question papers for Class 10 Mathematics similar to the actual board exam? |  |
| 4. Can solving CBSE sample question papers help in scoring better marks in Class 10 Mathematics? |  |
| 5. How can students effectively utilize CBSE sample question papers for Class 10 Mathematics preparation? |  |

















