Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Standard) - 1 | CBSE Sample Papers For Class 10 PDF Download
| Table of contents |

|
| Class XMathematics – StandardSample Question Paper 2020-21Max. Marks : 80Duration : 3 hrs. |

|
| General Instructions |

|
| Part – A |

|
| Part - B |

|
Class X
Mathematics – Standard
Sample Question Paper 2020-21
Max. Marks : 80
Duration : 3 hrs.
General Instructions
1. This question paper contains two parts A and B.
2. Both Part A and Part B have internal choices.
Part – A
1. It consists two sections- I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part – B
1. Section III, Question No. 21 to 26 are Very short answer Type questions of 2 marks each.
2. Section IV, Question No. 27 to 33 are Short Answer Type questions of 3 marks each.
3. Section V, Question No. 34 to 36 are Long Answer Type questions of 5 marks each.
4. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part – A
Section - I
Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
Q.1. If xy = 180 and HCF (x, y) = 3, then find the LCM (x, y). (1 Mark)
OR
The decimal representation of 14587 / 21 x 54 will terminate after how many decimal places? (1 Mark)
Ans. We know that,
► "LCM × HCF = Product of two numbers"
(LCM) (3) = 180
LCM = 60
OR
Four decimal places
Detailed Solution :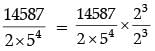
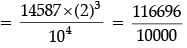
= 11.6696
Thus, the given rational number terminates after four decimal places.
Q.2. If the sum of the zeroes of the quadratic polynomial 3x2 – kx + 6 is 3, then find the value of k. (1 Mark)
Ans. Let the roots of the given quadratic equation α and β
► So we have,
α + β = k / 3
3 = k / 3
k = 9
Q.3. For what value of k, the pair of linear equations 3x + y = 3 and 6x + ky = 8 does not have a solution. (1 Mark)
Ans. System has no solution if
a1 / a2 = b1 / b2 ≠ c1 / c2
3 / 6 = 1 / k ≠ 3 / 8
3 / 6 = 1 / k
k = 2
OR
k not equal to 8 / 3.
Q.4. If 3 chairs and 1 table costs ₹ 1500 and 6 chairs and 1 table costs ₹ 2400. Form linear equations to represent this situation. (1 Mark)
Ans. Let the cost of 1 chair = ₹ x
and the cost of 1 table = ₹ y
According to question,
3x + y = 1500
and 6x + y = 2400
Q.5. Which term of the following A.P. 27, 24, 21,…..is zero? (1 Mark)
OR
In an Arithmetic Progression, if d = – 4, n = 7, an = 4, then find a. (1 Mark)
Ans. We know that an = a + (n – 1)d
► For l = 0
0 = 27 + (n – 1)(–3)
30 = 3n
n = 10
10th term of the given AP is zero
OR
an = a + (n – 1)d
4 = a + 6 × (– 4)
a = 28
Q.6. For what values of k, the given quadratic equation 9x2 + 6kx + 4 = 0 has equal roots? (1 Mark)
Ans. 9x2 + 6kx + 4 = 0
► For equal roots b2 – 4ac = 0
► Discriminant D = 0 so,
(6k)2 – 4 × 9 × 4 = 0
36k2 = 144
k2 = 4
k = ±2
Q.7. Find the roots of the equation x2 + 7x + 10 = 0. (1 Mark)
OR
For what value(s) of ‘a’ quadratic equation 3ax2 − 6x + 1 = 0 has no real roots? (1 Mark)
Ans. x2 + 7x +10 = 0
x2 + 5x + 2x + 10 = 0
(x + 5)(x + 2) = 0
Either x = – 5 or x = – 2
OR
Given that,
3ax2 – 6x + 1 = 0
► For no real roots b2 – 4ac < 0
► Discriminant D < 0 so,
(– 6)2 – 4(3a)(1) < 0
12a > 36
a > 3
Q.8. If PQ = 28 cm, then find the perimeter of ΔPLM. (1 Mark)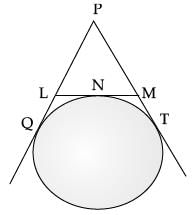 Ans. PQ = PT
Ans. PQ = PT
PL + LQ = PM + MT
PL + LN = PM + MN
(LQ = LN, MT = MN)
(Tangents to a circle from a common point)
Perimeter(ΔPLM)
= PL + LM + PM
= PL + LN + MN + PM
= 2(PL + LN)
= 2(PL + LQ)
= 2 × 28 = 56 cm
∵ LQ = LN
MT = MN
Tangents to a circle from a common point.
Q.9. If two tangents are inclined at 60˚ are drawn to a circle of radius 3 cm, then find length of each tangent. (1 Mark)
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP. (1 Mark)
Ans. 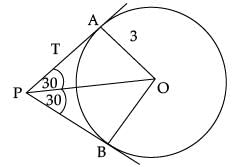
In ΔPAO,
tan 30° = AO / PA
(Using trigonometry)
1 / √3 = 3 / PA
PA = 3√3 cm
OR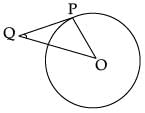
In ΔOPQ,
∠P + ∠Q + ∠O = 180°
(∠P = ∠Q isosceles triangle)
2∠Q + ∠P = 180°
2∠Q+90° =180°
2∠Q =90°
∠Q = 45°
Q.10. In the DABC, D and E are points on side AB and AC respectively such that DE || BC. If AE = 2 cm, AD = 3 cm and BD = 4.5 cm, then find CE. (1 Mark)
Ans. 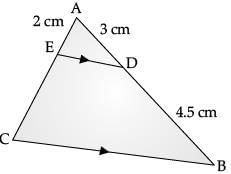 Using basic proportionality theorem:
Using basic proportionality theorem:
AD / BD = AE / CE [By using BPT]
3 / 4.5 = 2 / CE
CE = 3 cm
Q.11. In the figure, if B1, B2, B3,…... and A1, A2, A3,….. points have been marked at equal distances. On lines X and Y in what ratio does C divides AB? (1 Mark)
Ans. C divides AB internally in the ratio 8:5
Q.12. If sin A + cos B = 1, A = 30° and B is an acute angle, then find the value of B. (1 Mark)
Ans. sin 30° + cos B = 1
1 / 2 + cos B = 1
cos B = 1 / 2 = cos 60°
Q.13. If x = 2 sin2θ and y = 2 cos2θ + 1, then find the value of x + y. (1 Mark)
Ans. ∠B = 60°
x + y = 2 sin2θ + 2 cos2θ + 1
= 2(sin2θ + cos2θ) + 1
(As sin2x +cos2x = 1)
= 3
Q.14. In a circle of diameter 42 cm,if an arc subtends an angle of 60˚ at the centre where π = 22 / 7, then what will be the length of arc. (1 Mark)
Ans. Length of arc = θ / 360º (2πr)
60º / 360º = (2 x 22 / 7 x 21)
= 22 cm
Q.15. 12 solid spheres of the same radii are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. Find the diameter of the each sphere. (1 Mark)
Ans. R = radius of cylinder
H = height of cylinder
r = radius of sphere
πR2H =
1 × 1 × 16 =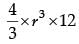
r3 = 1
r = 1
d = 2 cm.
Q.16. Find the probability of getting a doublet in a throw of a pair of dice. (1 Mark)
OR
Find the probability of getting a black queen when a card is drawn at random from a well-shuffled pack of 52 cards. (1 Mark)
Ans. Probability of getting a doublet = 1 / 6
Doublet means same number on both dice.
Detailed Solution
The outcomes when two dice are thrown together are:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
► Total number of outcomes = n(S) = 36
► Favourable outcomes are : (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) and (6, 6) i.e., n(E) = 6
► Required Probability = n(E) / n(S) = 6 / 36 = 1 / 6
OR
► Probability of getting a black queen = 2 / 52 = 1 / 26
Detailed Solution
► Total no. of cards = 52
► No. of black queens = 2
► So, Probability of black queen = 2 / 52 = 1 / 26
Section - II
Case study based questions are compulsory. Attempt any four subparts of each question. Each subpart carries 1 mark.
Q.17. Case Study Based-1
Sun Room
The diagrams show the plans for a sun room. It will be built onto the wall of a house. The four walls of the sun room are square clear glass panels. The roof is made using
- Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape
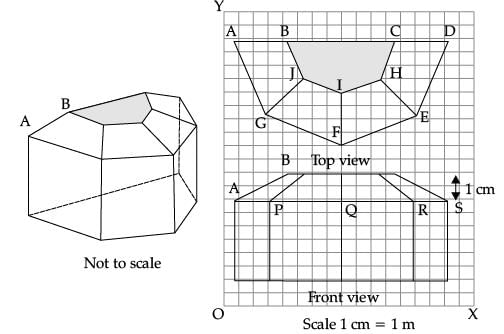
(i) Find the mid-point of the segment joining the points J (6, 17) and I (9, 16). (1 Mark)
(a) 33 / 2, 15 / 2
(b) 3 / 2, 1 / 2
(c) 15 / 2, 33 / 2
(d) 1 / 2, 3 / 2
Ans. (c)
Solution. Mid- point of J(6, 17) and I(9, 16) is
x = 15 / 2 and y = 33 / 2
(ii) The distance of the point P from the y-axis is (1 Mark)
(a) 4
(b) 15
(c) 19
(d) 25
Ans. (a)
(iii) The distance between the points A and S is (1 Mark)
(a) 4
(b) 8
(c) 16
(d) 20
Ans. (c)
(iv) Find the co-ordinates of the point which divides the line segment joining the points A and B in the ratio 1 : 3 internally. (1 Mark)
(a) (8.5, 2.0)
(b) (2.0, 9.5)
(c) (3.0, 7.5)
(d) (2.0, 8.5)
Ans. (d)
(v) If a point (x, y) is equidistant from the Q(9, 8) and S(17, 8), then (1 Mark)
(a) x + y = 13
(b) x – 13 = 0
(c) y – 13 = 0
(d) x – y = 13
Ans. (b)
Solution. Let point be P(x, y)
PQ2 = PS2
or, (x – 9)2 +(y – 8)2 = (x – 17)2 + (y – 8)2
or, x – 13 = 0
Q.18. Case Study Based- 2 Scale Factor And Similarity
Scale Factor:
A scale drawing of an object is of the same shape as the object but of a different size. The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The value of scale is written as a ratio.
Similar Figures:
The ratio of two corresponding sides in similar figures is called the scale factor.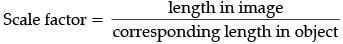
 If one shape can become another using Resizing then the shapes are Similar
If one shape can become another using Resizing then the shapes are Similar Hence, two shapes are Similar when one can become the other after a resize, flip, slide or turn.
Hence, two shapes are Similar when one can become the other after a resize, flip, slide or turn.
(i) A model of a boat is made on the scale of 1:4. The model is 120 cm long. The full size of the boat has a width of 60 cm. What is the width of the scale model? (1 Mark) (a) 20 cm
(a) 20 cm
(b) 25 cm
(c) 15 cm
(d) 240 cm
Ans. (c)
Solution. width of the scale model = 60 / 4 = 15 cm
(ii) What will effect the similarity of any two polygons? (1 Mark)
(a) They are flipped horizontally
(b) They are dilated by a scale factor
(c) They are translated down
(d) They are not the mirror image of one another
Ans. (d)
Solution. They are not the mirror image of one another
(iii) If two similar triangles have a scale factor of a:b. Which statement regarding the two triangles is true? (1 Mark)
(a) The ratio of their perimeters is 3a:b
(b) Their altitudes have a ratio a:b
(c) Their medians have a ratio a/2:b
(d) Their angle bisectors have a ratio a2: b2
Ans. (b)
Solution. Their altitudes have a ratio a : b
(iv) The length of shadow of a stick 5 m long is 2 m. At the same time the shadow of a tree 12.5 m high is (1 Mark)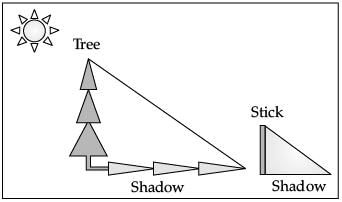 (a) 3 m
(a) 3 m
(b) 3.5 m
(c) 4.5 m
(d) 5 m
Ans. (d)
Solution. Let shadow of the tree be x.
By the property of similar triangle
we have 5 / 2 =12.5 / x
or, x = (12.5 × 2) / 5 = 5 cm
(v) Below you see a student's mathematical model of a farmhouse roof with measurements. The attic floor, ABCD in the model, is a square. The beams that support the roof are the edges of a rectangular prism, EFGHKLMN. E is the middle of AT, F is the middle of BT, G is the middle of CT, and H is the middle of DT. All the edges of the pyramid in the model have length of 12 m. What is the length of EF, where EF is one of the horizontal edges of the block? (1 Mark)
What is the length of EF, where EF is one of the horizontal edges of the block? (1 Mark)
(a) 24 m
(b) 3 m
(c) 6 m
(d) 10 m
Ans. (c)
Solution. Length of the horizontal edge EF
= half of the edge of pyramid
= 12 / 2
= 6 cm (as E is the mid point of AT)
Q.19. Case Study Based- 3
Applications of Parabolas-Highway Overpasses/Underpasses
A highway underpass is parabolic in shape.
Parabola
A parabola is the graph that results from p(x) = ax2 + bx + c.
Parabolas are symmetric about a vertical line known as the Axis of Symmetry.
The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the vertex.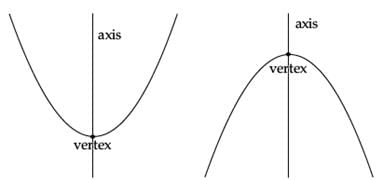
(i) If the highway overpass is represented by x2 – 2x – 8. Then its zeroes are (1 Mark)
(a) (2, – 4)
(b) (4, – 2)
(c) (– 2, – 2)
(d) (– 4, – 4)
Ans. (b)
Solution. x2 – 2x – 8 = 0
or, x2 – 4x + 2x – 8 = 0
or, x(x – 4) + 2(x – 4) = 0
or, (x – 4)(x + 2) = 0
or, x = 4, x = – 2
(ii) The highway overpass is represented graphically. Zeroes of a polynomial can be expressed graphically. Number of zeroes of polynomial is equal to number of points where the graph of polynomial (1 Mark)
(a) Intersects x-axis
(b) Intersects y-axis
(c) Intersects y-axis or x-axis
(d) None of the above
Ans. (a)
(iii) Graph of a quadratic polynomial is a (1 Mark)
(a) straight line
(b) circle
(c) parabola
(d) ellipse
Ans. (c)
(iv) The representation of Highway Underpass whose one zero is 6 and sum of the zeroes is 0, is (1 Mark)
(a) x2 – 6x + 2
(b) x2 – 36
(c) x2 – 6
(d) x2 – 3
Ans. (b)
Solution. x2 – 36 = 0
or, x = 6, – 6
(v) The number of zeroes that polynomial f(x) = (x – 2)2 + 4 can have is : (1 Mark)
(a) 1
(b) 2
(c) 0
(d) 3
Ans. (c)
Q.20. Case Study Based-4
100 m RACE
A stopwatch was used to find the time that it took a group of students to run 100 m.

(i) Estimate the mean time taken by a student to finish the race. (1 Mark)
(a) 54
(b) 63
(c) 43
(d) 50
Ans. (c)
Solution. 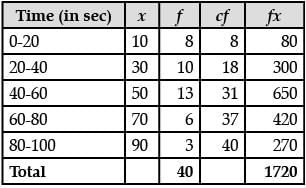
Mean = 1720 / 40 = 43
(ii) What will be the upper limit of the modal class? (1 Mark)
(a) 20
(b) 40
(c) 60
(d) 80
Ans. (c)
Solution. Modal class = 40 - 60
Upper limit = 60
(iii) The construction of cumulative frequency table is useful in determining the (1 Mark)
(a) Mean
(b) Median
(c) Mode
(d) All of the above
Ans. (b)
(iv) The sum of lower limits of median class and modal class is (1 Mark)
(a) 60
(b) 100
(c) 80
(d) 140
Ans. (c)
Solution. Median class = 40 - 60
Modal class = 40 - 60
Therefore, the sum of the lower limits of median and modal class = 40 + 40 = 80
(v) How many students finished the race within 1 minute? (1 Mark)
(a) 18
(b) 37
(c) 31
(d) 8
Ans. (c)
Solution. Number of students are: 8 + 10 + 13 = 31
Part - B
Section - III
All questions are compulsory. In case of internal choices, attempt any one.
Q.21. 3 bells ring at an interval of 4, 7 and 14 minutes. All three bells rang at 6 am, when the three bells will the ring together next? (2 Mark)
Ans. We know that,
The three bells again ring together on that time which is the LCM of individual time of each bell
4 = 2 × 2
7 = 7 × 1
14 = 2 × 7
LCM = 2 × 2 × 7 = 28
The three bells will ring together again at 6 : 28 am
Q.22. Find the point on x-axis which is equidistant from the points (2, – 2) and (– 4, 2). (2 Mark)
OR
P(–2, 5) and Q (3, 2) are two points. Find the co-ordinates of the point R on PQ such that PR = 2QR. (2 Mark)
Ans. Let P(x, 0) be a point on x-axis
PA = PB
PA2 = PB2
(x – 2)2 + (0 + 2)2 = (x + 4)2 + (0 – 2)2
x2 + 4 – 4x + 4 = x2 + 16 + 8x + 4 – 4x + 4
= 8x + 16
x = –1
Hence co-ordinate of point P(–1, 0)
OR
PR : QR = 2 : 1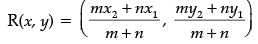
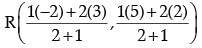
R(4 / 3, 3)
Q.23. Find a quadratic polynomial whose zeroes are 5 − 3√2 and 5 + 3√2. (2 Mark)
Ans.
► Sum of zeroes = 5 − 3√2 + 5+ 3√2 = 10
► Product of zeroes = (5 − 3√2)(5+ 3√2) = 7
► Polynomial is given by
x2 – (sum of zeroes) x + (product of zeroes) = 0
P(x) = x2 – 10x + 7
Q.24. Draw a line segment AB of length 9 cm. With A and B as centres, draw circles of radius 5 cm and 3 cm respectively. Construct tangents to each circle from the centre of the other circle. (2 Mark)
Ans. 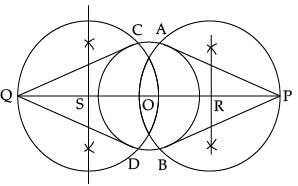 Detailed Solution
Detailed Solution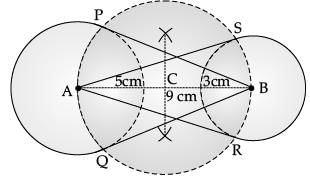
Steps of Construction
1. Draw a line segment AB of 9 cm.
2. Taking A and B as centres draw two circles radii of 5 cm and 3 cm respectively.
3. Bisect the line AB. Let mid-point of AB be C.
4. Taking C as centre draw a circle of radius AC which intersects the two circles at point P, Q, R and S.
5. Join BP, BQ, AS and AR.
BP, BQ and AR, AS are the required tangents.
Q.25. If tan A = 3 / 4, find the value of 1 / sin A + 1 / cos A (2 Mark)
OR
If √3 sin θ – cos θ = 0 and 0˚< θ < 90˚, then find the value of θ. (2 Mark)
Ans. Given that, tan A = 3 / 4 = 3k / 4k
sin A = 3k / 5k = 3 / 5
cos A = 4k / 5k = 4 / 5
1 / sin A + 1 / cos A = 5 / 3 + 5 / 4
= 20 + 15 / 12
= 35 / 12
OR
√3 sin θ = cos θ
sin θ / cos θ = 1 / √3
tan θ = 1 / √3
θ = 30°
Q.26. In the figure, quadrilateral ABCD is circumscribing a circle with centre O and AD ⊥ AB. If radius of incircle is 10 cm, then find the value of x. (2 Mark)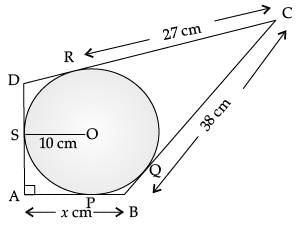 Ans. ∠A = ∠OPA = ∠OSA = 90°
Ans. ∠A = ∠OPA = ∠OSA = 90°
∠SOP = 90°
Also, AP = AS
Hence, OSAP is a square.
AP = AS = 10 cm
CR = CQ = 27 cm
BQ = BC – CQ
= 38 – 27 = 11 cm
BP = BQ = 11 cm
x = AB = AP + BP
= 10 + 11 = 21 cm
Section - IV
All questions are compulsory. In case of internal choices, attempt any one.
Q.27. Prove that 2 − √3 is irrational, given that √3 is irrational. (3 Mark)
Ans. Let 2 − √3 be a rational number
We can find co-primes numbers a and b (b ≠ 0) such that
2 − √3 = a / b
2 - a / b = √3
So, we get 2b - a / b = √3
Since a and b are integers, we get 2b - a / b = √3 is irrational and so √3 is rational. But √3 is an irrational number.
Which contradicts our statement
Therefore 2 − √3 is irrational.
Q.28. If one root of the quadratic equation 3x2 + px + 4 = 0 is 2 / 3, then find the value of p and the other root of the equation. (3 Mark)
OR
The roots α and β of the quadratic equation x2 – 5x + 3(k – 1) = 0 are such that α – β = 1. Find the value k. (3 Mark)
Ans. 3x2 + px + 4 = 0
∵ 2 / 3 is a root so it must satisfy the given equation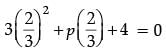

On solving we get
p = –8
3x2 – 8x + 4 = 0
3x2 – 6x – 2x + 4 = 0
3x(x – 2) – 2(x – 2) = 0
x = 2 / 3 or x = 2
Hence, x = 2
So the other root is 2.
OR
We have α + β = 5 ...(i)
α – β = 1 ...(ii)
Solving (i) and (ii), we get
α = 3 and β = 2
also αβ = 6
or 3(k – 1) = 6
k – 1 = 2
k = 3
Q.29. In the figure, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region. (3 Mark)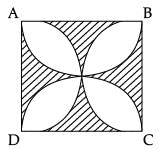 Ans. Area of 1 segment = area of sector – area of triangle
Ans. Area of 1 segment = area of sector – area of triangle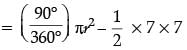
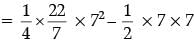
= 14 cm2
► Area of 8 segments = 8 × 14 = 112 cm2
► Area of the shaded region = 14 × 14 – 112
= 196 – 112 = 84 cm2
(each petal is divided into 2 segments)
Q.30. In an equilateral triangle ABC, D is a point on side BC such that BD = 1 / 3 BC. Prove that 9 AD2 = 7 AB2. (3 Mark)
Ans.  Construction: Draw AM ⊥ BC
Construction: Draw AM ⊥ BC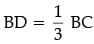
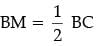
In ΔABM, AB2 = AM2 + BM2
= AM2 + (BD + DM)2
= AM2 + DM2 + BD2 + 2BD.DM
= AD2 + BD2 + 2BD (BM – BD)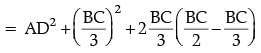
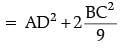
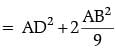
Hence, 7AB2 = 9AD2
Q.31. The Median of the following data is 16. Find the missing frequencies a and b, if the total of the frequencies is 70. (3 Mark)
Ans. 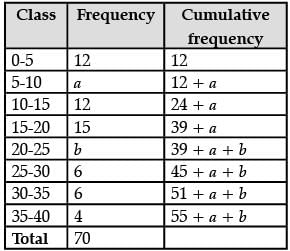
55 + a + b = 70
a + b = 15
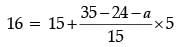
1 = (11 – a) / 3
a = 8
55 + a + b = 70
55 + 8 + b = 70
b = 7
Q.32.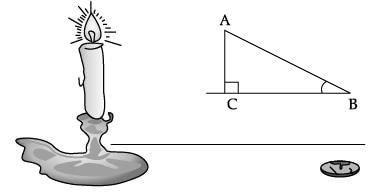 If the angles of elevation of the top of the candle from two coins distant ‘a’ cm and ‘b’ cm (a > b) from its base and in the same straight line from it are 30˚ and 60˚, then find the height of the candle. (3 Mark)
If the angles of elevation of the top of the candle from two coins distant ‘a’ cm and ‘b’ cm (a > b) from its base and in the same straight line from it are 30˚ and 60˚, then find the height of the candle. (3 Mark)
Ans. 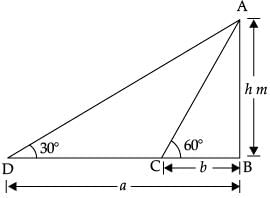 ► Let AB = candle C and D are Points
► Let AB = candle C and D are Points
tan 60° = AB / BD = h / b
√3 = h / b
h = b√3 ...(i)
tan 30° = AB / BD
1 / √3 = h / b
h = a / √3
► Multiplying (i) and (ii), we get
h2 = ba
h = √ab m
Q.33. The mode of the following data is 67. Find the missing frequency x. (3 Mark)
Ans. 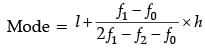
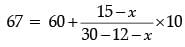
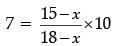
7 × (18 – x) = 10(15 – x)
126 – 7x = 150 – 10x
3x = 150 – 126
3x = 24
x = 8
Section - V
All questions are compulsory. In case of internal choices, attempt any one.
Q.34. The two palm trees are of equal heights and are standing opposite to each other on either side of the river, which is 80 m wide. From a point O between them on the river the angles of elevation of the top of the trees are 60° and 30°, respectively. Find the height of the trees and the distances of the point O from the trees. (5 Mark)
OR
The angles of depression of the top and bottom of a building 50 meters high as observed from the top of a tower are 30˚ and 60˚ respectively. Find the height of the tower, and also the horizontal distance between the building and the tower. (5 Mark)
Ans. 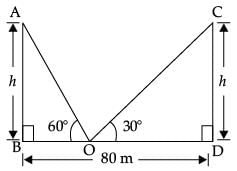
► Let BD = river
AB = CD = palm trees = h
BO = x
OD = 80 – x
In ΔABO,
tan 60° = h / x
√3 = h / x
h = √3x
In ΔCDO,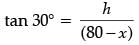
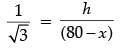 ...(ii)
...(ii)
► Solving (i) and (ii), we get
x = 20
h = 3x [From eqn. (i)]
= 34.6
► The height of the trees = h = 34.6 m
BO = x = 20 m
DO = 80 – x
= 80 – 20
= 60 m
OR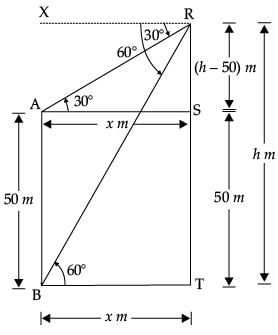 ► Let AB = Building of height 50 m
► Let AB = Building of height 50 m
RT = tower of height = h m
BT = AS = x m
AB = ST = 50 m
RS = TR – TS = (h – 50)m
In ΔARS, tan 30° = RS / AS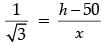 ..(i)
..(i)
► In ΔRBT, tan 60° = RT / BT
√3 = h / x
► Solving (i) and (ii), we get
h = 75
► From (ii), x = h / √3 = 75 / √3
= 25√3
► Hence, height of the tower = h = 75 m
► Distance between the building and the tower
= 25√3
= 43.25 m
Q.35. Water is flowing through a cylindrical pipe of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm at the rate of 0.7 m/sec. By how much will the water rise in the tank in half an hour? (5 Mark)
Ans. For pipe, r = 1 cm
Length of water flowing in 1 sec,
h = 0.7 m = 7 cm
Cylindrical Tank, R = 40 cm
rise in water level = H
Volume of water flowing in 1 sec
= πr2h = π × 1 × 1 × 70
= 70π
Volume of water flowing in 60 sec =70π × 60
Volume of water flowing in 30 minutes
= 70π × 60 × 30
Volume of water in tank = πr2H
= π × 40 × 40 × H
Volume of water in tank
= Volume of water flowing in 30 minutes
π × 40 × 40 × H = 70π × 60 × 30
H = 78.75 cm
Q.36. A motorboat covers a distance of 16 km upstream and 24 km downstream in 6 hours. In the same time it covers a distance of 12 km upstream and 36 km downstream. Find the speed of the boat in still water and that of the stream. (5 Mark)
Ans. Let speed of the boat in still water = x km/hr, and speed of the current = y km/hr
Downstream speed = (x + y) km/hr
Upstream speed = (x − y) km/hr ...(i)
...(i) ...(ii)
...(ii)
Let
and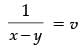
Put in the above equation, we get
24u + 16v = 6
or, 12u + 8v = 3 ...(iii)
36u + 12v = 6
or, 6u + 2v = 1 ...(iv)
Multiplying (iv) by 4, we get
24u + 8v = 4 ...(v)
Subtracting (iii) by (v), we get
12u = 1
⇒ u = 1 / 12
Putting the value of u in (iv), we get, v = 1 / 4
⇒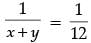
and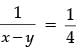
⇒ x + y = 12 and x − y = 4
Thus, speed of the boat in still water = 8 km/hr,
Speed of the current = 4 km/hr
|
303 docs|7 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Standard) - 1 - CBSE Sample Papers For Class 10
| 1. What is the maximum marks for the Class X Mathematics Standard Sample Question Paper? |  |
| 2. How long is the duration for the Class X Mathematics Standard Sample Question Paper? |  |
| 3. What are the general instructions for the Class X Mathematics Standard Sample Question Paper? |  |
| 4. Is the Class X Mathematics Standard Sample Question Paper divided into parts A and B? |  |
| 5. Are there any specific instructions mentioned for both Part A and Part B of the Class X Mathematics Standard Sample Question Paper? |  |

|
Explore Courses for Class 10 exam
|

|


















