Set Theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
What is a Set
- Set theory is a part of math that looks at groups of things and how we can work with them.
- A set is just a bunch of things together. Like if you have a bunch of players in a soccer team, that's a set, and each player is a part of it.
- Words like collection, group, and class mean the same thing as set. And elements, members, and objects all mean the individual things inside the set.
- Set is a well-defined collection of objects or people.
- Example:
A set of Natural Numbers is given by:
N = {1, 2, 3, 4…..}
The above example is a collection of natural numbers and is also well-defined. Well-defined means, that anyone should be able to tell whether the object belongs to the set or not.

Set Symbols
Important Terms Related to Sets
Elements of a Set
- The objects contained by a set are called the elements of the set.
- They are represented using the ∈ symbol which means “belongs to”.
- For Example:
In the set of Natural Numbers, 1, 2, 3, etc. are the objects, hence they are the elements of the set of Natural Numbers.
We can also say that 1 belongs to set N and it is represented as 1 ∈ N.

Cardinal Number of a Set
- The number of elements present in a set is called the Cardinal Number of a Set.
- For Example:
Suppose P is a set of the first five prime numbers given by P = {2, 3, 5, 7, 11}, then the Cardinal Number of set P is 5.
The Cardinal Number of Set P is represented by n(P) or |P| = 5.
Representation of Sets
Sets can be represented in two ways:
1. Roster Form or Tabular form
2. Set Builder Form

1. Roster Form
- In roster form, all the elements of the set are listed, separated by commas and enclosed between curly braces { }.
- Example: If set represents all the leap years between the year 1995 and 2015, then it would be described using Roster form as:
A ={1996,2000,2004,2008,2012} - Now, the elements inside the braces are written in ascending order. This could be descending order or any random order. As discussed before, the order doesn’t matter for a set represented in the Roster Form.
- Also, multiplicity is ignored while representing the sets. E.g. If L represents a set that contains all the letters in the word ADDRESS, the proper Roster form representation would be
- L ={A,D,R,E,S }= {S,E,D,A,R}
L≠ {A,D,D,R,E,S,S}
2. Set Builder Form
- In set builder form, all the elements have a common property. This property is not applicable to the objects that do not belong to the set.
- Example: If set S has all the elements which are even prime numbers, it is represented as:
S={ x: x is an even prime number} - where ‘x’ is a symbolic representation that is used to describe the element.
- ‘:’ means ‘such that’
- ‘{}’ means ‘the set of all’
- So, S = { x:x is an even prime number } is read as ‘the set of all x such that x is an even prime number’. The roster form for this set S would be S = 2. This set contains only one element. Such sets are called singleton/unit sets.
Types of Sets


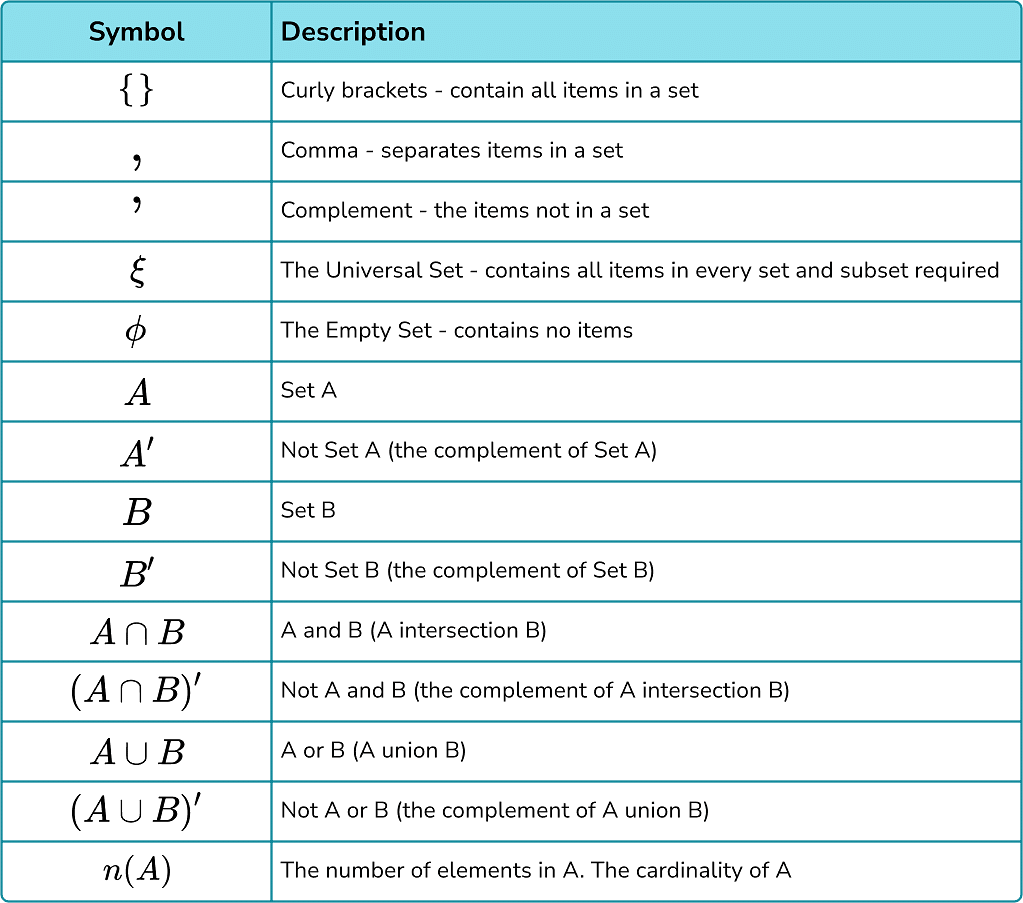
Set Theory Symbols
Given below are all symbols that are used in set theory:
Set Operations
1. Union (U):
- The combination of elements from two sets, including duplicates.
- Example:
If Set A = {1, 3, 5} and Set B = {2, 3, 4}, then A U B = {1, 2, 3, 4, 5}
2. Intersection (∩):
- The collection of elements that are in both sets.
- Example:
If Set A = {1, 3, 5} and Set B = {2, 3, 4}, then A ∩ B = {3}
3. Difference (\):
- The collection of elements in the first set that are not in the second set.
- Example:
If Set A = {1, 3, 5} and Set B = {2, 3, 4}, then A \ B = {1, 5}
4. Complement (A’):
- The collection of elements that are not in the first set, but are in the universal set.
- Example:
If Universal Set = {1, 2, 3, 4, 5} and Set A = {2, 4}, then A’ = {1, 3, 5}
5. Cartesian Product (A x B):
- The collection of ordered pairs where the first element comes from the first set and the second element comes from the second set.
- Example:
If Set A = {1, 2} and Set B = {a, b}, then A x B = {(1, a), (1, b), (2, a), (2, b)}
Properties of Set Operations

Set Theory Formulas
- For the size of the union of two overlapping sets A and B:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B) - For the size of the intersection of two overlapping sets A and B:
n(A ∩ B) = n(A) + n(B) – n(A ∪ B) - For the size of set A in terms of its overlap with set B:
n(A) = n(A ∪ B) + n(A ∩ B) – n(B) - For the size of set B in terms of its overlap with set A:
n(B) = n(A ∪ B) + n(A ∩ B) – n(A) - For the size of set A excluding the elements also in set B:
n(A – B) = n(A ∪ B) – n(B)
n(A – B) = n(A) – n(A ∩ B) - For the size of the union of three sets A, B, and C:
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n(C∩A) + n(A∩B∩C) - Disjoint Sets

Examples
Q1: If U = {a, b, c, d, e, f}, A = {a, b, c}, B = {c, d, e, f}, C = {c, d, e}, find (A ∩ B) ∪ (A ∩ C).
Sol: A ∩ B = {a, b, c} ∩ {c, d, e, f}
A ∩ B = { c }
A ∩ C = { a, b, c } ∩ { c, d, e }
A ∩ C = { c }
∴ (A ∩ B) ∪ (A ∩ C) = { c }
Q2: Give examples of finite sets.
Sol: The examples of finite sets are:
Set of months in a year
Set of days in a week
Set of natural numbers less than 20
Set of integers greater than -2 and less than 3
Q3: If U = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11}, A = {3, 5, 7, 9, 11} and B = {7, 8, 9, 10, 11}, Then find (A – B)′.
Sol: A – B is a set of member which belong to A but do not belong to B
∴ A – B = {3, 5, 7, 9, 11} – {7, 8, 9, 10, 11}
A – B = {3, 5}
According to formula,
(A − B)′ = U – (A – B)
∴ (A − B)′ = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11} – {3, 5}
(A − B)′ = {2, 4, 6, 7, 8, 9, 10, 11}.
Q4: If A and B are two sets such that n(A) = 17, n(B) = 23 and n(A ∪ B) = 38 then find n(A ∩ B).
Sol: We know that n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
⇒ 38 = 17 + 23 – n(A ∩ B)
⇒ n(A ∩ B) = 40 – 38 = 2
Q5: If X = {1, 2, 3, 4, 5}, Y = {4, 5, 6, 7, 8}, and Z = {7, 8, 9, 10, 11}, find (X ∪ Y), (X ∪ Z), (Y ∪ Z), (X ∪ Y ∪ Z), and X ∩ (Y ∪ Z)
Sol: (X ∪ Y) = {1, 2, 3, 4, 5} ∪ {4, 5, 6, 7, 8} = {1, 2, 3, 4, 5, 6, 7, 8}
(X ∪ Z) = {1, 2, 3, 4, 5} ∪ {7, 8, 9, 10, 11} = {1, 2, 3, 4, 5, 7, 8, 9, 10, 11}
(Y ∪ Z) = {4, 5, 6, 7, 8} ∪ {7, 8, 9, 10, 11} = {4, 5, 6, 7, 8, 9, 10, 11}
(X ∪ Y ∪ Z) = {1, 2, 3, 4, 5} ∪ {4, 5, 6, 7, 8} ∪ {7, 8, 9, 10, 11} = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
X ∩ (Y ∪ Z) = {1, 2, 3, 4, 5} ∩ {4, 5, 6, 7, 8, 9, 10, 11} = {4, 5}
|
88 videos|119 docs|91 tests
|
FAQs on Set Theory - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What is a set in set theory? |  |
| 2. What are some common set symbols used in set theory? |  |
| 3. How are sets represented in set theory? |  |
| 4. What are some important terms related to sets in set theory? |  |
| 5. What are some common set operations in set theory? |  |
|
88 videos|119 docs|91 tests
|

|
Explore Courses for CAT exam
|

|


















