Short & Long Answer Questions: Systems of Particles & Rotational Motion | Physics for EmSAT Achieve PDF Download
Q.1 What is the advantage of the concept of centre of mass?
Answer: Centre of mass helps us to describe the behaviour of a macroscopic body in terms of the laws developed for the microscopic bodies. If we are not concerned with the internal motion and structure of a system, the gross motion of the system can be analysed by applying Newton's laws of motion to the CM of the system which is a point where the entire mass of the system may be assumed to be concentrated and where all the external forces are assumed to apply.
Q.2 Should the centre of mass of a body necessarily lie inside the body?
Answer: Not necessarily. For example, the CM of a ring lies in its hollow portion.
Q.3 Does the centre of mass of a solid necessarily lie within the body? If not, give an example.
Answer: No. For example, the CM of L-shaped rod lies in the region outside the rod.
Q.4 Is centre of mass a reality?
Answer: No. The centre of mass of a system is a hypothetical point which acts as a single mass particle of the system for an external force.
Q.5 Is it correct to say that the centre of mass of a system particles is always given by the average Position vectors of the constituent particles? If not, when is this statement true?
Answer: No. This is true when all the particles of the system are of same mass.
Q.6 If two particles of masses m1 and m2 move velocities υ1 and υ2 towards each other on a smooth horizontal table, what is the velocity of their centre of mass?
Answer:
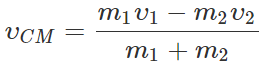
Q.7 Name the physical quantity that corresponds to the moment of force. On what factors does it depend?
Answer: The moment of force is called torque. It depends on (i) the magnitude of force, (ii) the perpendicular distance of the line of action of force from the axis of rotation.
Q.8 What happens to the moment of force about a point, if the line of action of the force moves towards the point?
Answer: Moment of force =Force × the perpendicular distance of the line of action of force "from" the axis of rotation. Hence the moment of force about a point decreases if the line of action of the force moves towards that point.
Q.9 A body is in rotational motion. Is it necessary that a torque be acting on it?
Answer: No, torque is required only for angular acceleration.
Q.10 Why do we prefer to use a wrench of longer aim?
Answer: The torque applied on the nut by the wrench is equal to the force multiplied by the perpendicular distance from the axis of rotation. Hence to increase torque a wrench of longer arm is preferred.
Q.11 Why in hand driven grinding machine, handle is put near the circumference of the stone or wheel?
Answer: For a given force, torque can be increased if the perpendicular distance of the point of application of the force from the axis of rotation is increased. Hence the handle put near the circumference produces maximum torque.
Q.12 It is difficult to open the door by pushing it or pulling it at the hinge. Why?
Answer: When the force is applied at the hinges, the line of action of the force passes through the axis of rotation i.e., r= 0, so τ F sinθ=0.. So we cannot open the door by pushing or pulling it at the hinges.
Q.13 Why a force is applied at right angles to the heavy door at the outer edge while closing or opening it?
Answer: Torque, τ=rFsinθ. For a force applied at right angle to the outer edge of the door both sinθ(=sin90∘=1)and r are maximum. Hence the torque produced is maximum.
Q.14 A man climbs a tall, old step ladder that has a tendency to sway. He feels much more unstable when standing near the top than when near the bottom. Why?
Answer: When the man stands at the top of step ladder it increases its distance from the point of contact, the point about which it can slip (rotate). The torque exerted is equal of rF. Hence larger the r, more are the chances to sway away.
Q.15 Why it is easier to open a tap with two fingers than with one finger?
Answer: With two fingers, we apply a couple whose moment is equal to the product of the force and perpendicular distance between the two fingers (which is equal to the length of the handle of the tap). When we apply force with one finger, an equal and opposite force of reaction acts at the axis of rotation. This results in a couple of smaller arm and hence lesser moment. So it is easier to open a tap with two fingers than with one finger.
Q.16 A faulty balance with unequal arms has its beam horizontal. Are the weights of the two pans equal?
Answer: They are of unequal mass. Their masses are in the inverse ratio of the arms of the balance.
Q.17 Can the couple acting on a rigid body produce translatory motion?
Answer: No, the couple acting on a rigid body cannot produce translatory motion; it can cause only rotation motion as the resultant force is zero.
Q.18 A labourer standing near the top of an old wooden step ladder feels unstable. Why?
Answer: The ladder can rotate about the point of contact of the ladder with the ground. When the labourer is at the top of the ladder, the lever arm of the force large. Hence the turning effect on the ladder will be large.
Q.19 Which physical quantities are expressed by the following: (i) the rate of change of angular momentum, and (ii) moment of linear momentum ?
Answer: (i) Torque, (ii) Angular momentum.
Q.20 If no external torque acts on a body, will its angular velocity remain conserved?
Answer: No. Angular velocity is not conserved but angular momentum is conserved.
Q.21 When a labourer cuts down a tree, he makes a cut on the side facing the direction in which he wants it to fall. Why?
Answer: The weight of tree exerts a torque about the point where the cut is made. This causes rotation of the tree about the cut.
Q.22 Define the term angular impulse.
Answer: The angular impulse acting on a body is the change of angular momentum of the body about a given axis.
Q.23 Which component of linear momentum does not contribute to angular momentum?
Answer: The radial component of linear momentum does not contribute to angular momentum.
Q.24 A particle revolves uniformly along a circular path, on a smooth horizontal table, by means of a string connected to it. Does its angular momentum change, if the string is suddenly cut?
Answer: No. The angular momentum remains unaltered when the string is cut.
Q.25 A heavenly body (such as a comet) revolves around a massive star in a highly elliptical orbit. Is its angular momentum constant over the entire orbit? (Ignore any mass loss of the comet when it comes too close to the star).
Answer: The heavenly body revolves around the massive star under the effect of gravitational force, which is purely radial. The torque exerted by such a force is zero. Hence the angular momentum of the heavenly body remains constant over its entire orbit.
Q.26 A projectile acquires angular monies turn about the point of projection during its flight. Does it violate the conservation of angular momentum?
Answer: A projectile will not acquire angular momentum, if no external force acts on it. However during its flight, the projectile is acted upon by the force of gravity and acquires angular momentum.
Q.27 Is a body in circular motion in equilibrium?
Answer: No. A body in circular motion has a centripetal acceleration 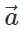 directed towards the centre of the circle. Since
directed towards the centre of the circle. Since 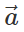 ≠0, the body is not in equilibrium.
≠0, the body is not in equilibrium.
Q.28 When is a body lying in a gravitation field in stable equilibrium?
Answer: A body in a gravitation field will be in stable equilibrium if the vertical line through its centre of gravity passes through the base of the body.
Q.29 Can a body in equilibrium while in motion? If yes, give an example.
Answer: Yes. A body in motion will be in equilibrium if it has no linear and angular accelerations. Hence a body moving with uniform velocity along a straight line will be in equilibrium.
Q.30 The bottom of a ship is made heavy. Why?
Answer: The bottom of a ship is made heavy so that its centre of gravity remains low. This ensures the stability of its equilibrium.
Q.31 Why does a girl lean towards right while carrying a bag in her left hand?
Answer: When the girl carries a bag in her left hand, her CG shifts towards left. In order to bring it in the middle (for stability of equilibrium), the girl has to lean towards her right.
Q.32 Some heavy boxes are to be loaded along with some empty boxes on a cart. Which boxes should be put on the cart first and why?
Answer: The heavy boxes should be loaded first so that the CG of the loaded cart remains in the lowest position. This ensures stability of equilibrium.
Q.33 Standing is not allowed in a double decker bus. Why?
Answer: When the passengers stand in the upper deck, the CG of the loaded bus is raised which makes it less stable.
Q.34 Why we cannot rise from a chair without bending a little forward?
Answer: Our weight exerts a torque about our feet. This makes difficult for us to rise from the chair. When we bend forward, the CG of our body comes above our feet. The torque due to our weight becomes zero and we can easily rise from the chair.
Q.35 A system is in stable equilibrium. What can we say about its potential energy?
Answer: The potential energy of the system is minimum.
Q.36 Why is moment of inertia also called rotational inertia?
Answer: The moment of inertia gives a measure of inertia in rotational motion. So it is also called rotational inertia.
Q.37 Give the physical significance of moment of inertia.
Answer: The moment of inertia plays the same role in rotatory motion as the mass does in translatory motion. It gives a measure of inertia in rotational motion.
Q.38 Does moment of inertia of a body r change with the change of the axis of rotation?
Answer: Yes. The moment of inertia of a body changes with the change in position and orientation of the axis of rotation.
Q.39 Does the moment of inertia of a rigid body change with the speed of rotation?
Answer: No, because the moment of inertia depends upon the axis of rotation and the distribution of mass.
Q.40 About which axis, the moment of inertia of a body is minimum?
Answer: The moment of inertia of a body is mini- mum about an axis passing through its centre of mass.
Q.41 Can the mass of body be taken to be concentrated at its centre of mass for the purpose of calculating its rotational inertia?
Answer: No. The moment of inertia greatly depends on the distribution of mass about the axis of rotation.
Q.42 About which axis would a uniform cube have a minimum rotational inertia?
Answer: About a diagonal, because the mass is more concentrated about a diagonal.
Q.43 Is radius of gyration a constant quantity?
Answer: No. It changes with the change in position of the axis of rotation.
Q.44 Does the radius of gyration depend upon the speed of rotation of the body?
Answer: No, it depends only on the distribution of mass of the body.
Q.45 Two lenses of same mass and same radius are given. One is convex and other is concave. Which one will have greater moment of inertia, when rotating about an axis perpendicular to the plane and passing through the centre?
Answer: The concave lens will have greater moment of inertia because the concave lens is thin at its centre and its mass is more concentrated at the outer edge.
Q.46 A disc is recast into a thin walled cylinder of same radius. Which will have large moment of inertia?
Answer: Hollow cylinder will have larger moment of inertia because most of its mass is located at comparatively larger distance from the axis of rotation.
Q.47 Two solid spheres of the same mass are made of metals of different densities. Which of them has a larger moment of inertia about the diameter? Why?
Answer: The sphere with small density will have larger radius and hence large moment of inertia.
Q.48 What is the advantage of the flywheel?
Answer: In case of a flywheel, the whole mass is practically near the rim which is situated far away from the axis of rotation. This is done to increase the moment of inertia of the wheel, thereby making the motion smooth and less jerky.
Q.49 Why spokes are provided in a bicycle wheel?
Answer: By connecting to the rim of wheel to the axle through the spokes, the mass of the wheel gets concentrated at its rim. This increases its moment of inertia. This ensures its uniform speed.
Q.50 Will two spheres of equal masses, one solid and the other hollow have equal moments of inertia? Give reason.
Answer: The hollow sphere will have a greater moment of inertia because its entire mass is concentrated at the boundary of the sphere i.e., at maximum distance from the axis of rotation.
Q.51 Why is it more difficult to revolve a stone tied to a large string than a stone tied to a smaller string?
Answer: The length of the string increases the distance of rotating mass from the axis of rotation and hence moment of inertia of the system is increased. Now, τ=Iαa thus a system with large moment of inertia requires large torque for its rotation.
Q.52 Two satellites of equal masses, which can be considered as particles are orbiting the earth at different heights? Will their moments of inertia be same or different?
Answer: M.I. of a satellite, I=Mr2 i.e., I ∝ r2 Hence the two satellites orbiting the earth at different heights will have different moments of inertia. The satellite orbiting at a larger height will have a larger moment of inertia.
Q.53 What is the use of flywheel in railway engine?
Answer: In a flywheel, most of the mass is concentrated at its rim. So it has a large moment of inertia. Any change of angular momentum imparted to the wheel by the piston results in a lesser change of angular velocity(L=Iω or ω=L/I ). Moreover, a flywheel stores a large amount of rotational energy(1/2 Iω2). This helps the wheel c fly off the dead point.
Q.54 There is a stick half of which is wooden is and half is of steel. It is pivoted at the wooden end and a force is applied at the steel end at right angles to its length. Next, it is pivoted at the steel end and the same force is applied at the wooden end. In which case is the angular acceleration more and why?
Answer: The distribution of mass is farther from the axis of rotation in the first case than in the second case. So the moment of inertia is more in first case than in second case, but the applied torque τ is same in both cases. Asτ=Iα or α=τ/I,, so the angular acceleration α is less in first case than in second case.
Q.55 Is the angular momentum of a system always conserved? If not, under what condition is it conserved?
Answer: No, angular momentum of a system is not always conserved. It is conserved only when no external torque acts on the system.
Q.56 A flywheel is revolving with a constant angular velocity. A chip of its rim breaks and flies away. What will be the effect on its angular velocity?
Answer: Due to the decrease in its mass, the moment of inertia of the flywheel will decrease. To conserve angular momentum, the angular velocity of the flywheel will increase.
Q.57 A cat is able to land on its feet after a fall. Why?
Answer: When a cat falls to ground from a height, it stretches its body along with the tail so that its moment of inertia becomes high. Since Iω is to remain constant, the value of angular speed ω decreases and therefore the cat is able to land on the ground gently.
Q.58 Why there are two propellers in a helicopter?
Answer: If there were only one propeller in the helicopter then, due to conservation of angular momentum, the helicopter itself would have turned in the opposite direction.
Q.59 The speed of a whirl wind in a tornado is alarmingly high. Why?
Answer: In a whirl wind, the air from nearby region gets concentrated in a small space thereby decreasing the value of moment of inertia considerably. Since, Iω=constant, due to decrease in moment of inertia, the angular speed becomes quite high.
Q.60 If earth contracts to half its radius, what would be the length of the day?
Answer: The moment of inertia (I=2/5 MR2) of the earth about its own axis will become one fourth and so its angular velocity will become four times L=Iω= constant). Hence the time period will reduce to one fourth (T=2π/ω)i.e., 6 hours.
Q.61 Two boys of the same weight sit at the opposite ends of a diameter of a rotating circular table. What happens to the speed of rotation if they move nearer to the axis of rotation?
Answer: The moment of inertia of the system /circular table + two boys) decreases. To conserve angular momentum (L=Iω=constant), the speed of rotation of the circular table increases.
Q.62 A thin wheel can stay up right on its rim for a considerable length of time when rolled with a considerable velocity, while it falls from its upright position at the slightest disturbance when stationary. Give reason.
Answer: When the wheel is rolling upright, it has angular momentum in the horizontal direction i.e., along the axis of the wheel. Because the angular momentum is to remain conserved, the wheel does not fall from its upright position because that would change the direction of angular momentum. The wheel falls only when it loses its angular velocity due to friction.
Q.63 A person is standing on a rotating table with metal spheres in his hands. If he withdraws his hands to his chest, what will be the effect on his angular velocity?
Answer: When the person withdraws his hands to his chest, his moment of inertia decreases. No external torque is acting on the system. So to conserve angular momentum, the angular velocity increases.
Q.64 A circular turn table rotates at constant angular velocity about a vertical axis. There is no friction and no driving torque. An ice pan containing ice also rotates with it. The ice melts but none of the water escapes from the pan. Is the velocity now greater, the same or less than the original velocity? Give reason.
Answer: Due to accumulation of water near the edge, the moment of inertia of the system increases. To conserve angular momentum, the angular velocity of the system decreases.
Q.65 Many rivers flow towards the equator. What effect does the sediment they carry to the seas have on the rotation of the earth?
Answer: The rivers carry sediments away from the axis of rotation of the earth. This increases the rotational inertia the earth. To conserve angular momentum, the rotational speed of the earth decreases.
Q.66 The moments of inertia of two rotating bodies A and B are IA and IB(IA>IB)and their angular momenta are equal. Which one has greater kinetic energy?
Answer: Angular momentum, L=Iω K.E. of rotation, 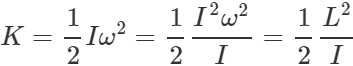 For constant L, K ∝ 1/I. As IA>IB ∴ KA<KB or KB>KA. So body B has a greater rotational K.E.
For constant L, K ∝ 1/I. As IA>IB ∴ KA<KB or KB>KA. So body B has a greater rotational K.E.
Q.67 If angular momentum is conserved in a system whose moment of inertia is decreased, will its rotational kinetic energy be conserved?
Answer: Here L=Iω=constant Rotational K.E. is given by  For constant L, K ∝ 1/I So when the moment of inertia decreases, the rotational K.E. increases. Hence rotational K.E. is not conserved.
For constant L, K ∝ 1/I So when the moment of inertia decreases, the rotational K.E. increases. Hence rotational K.E. is not conserved.
Q.68 How does an ice-skater, a ballet dancer or an acrobat take advantage of the principle of conservation of angular momentum?
Or
How does a ballet dancer vary her angular speed by outstretching her arms and legs?
Answer: An ice-skater, a ballet dancer or an acrobat is able to change his angular speed during the course of the performance. When the performer stretches out his hands and legs, his moment of inertia increases and the angular speed decreases. On the other hand, when he folds his hands and the legs near his body, the moment of inertia decreases and he is able to increase the angular speed.
Q.69 If earth were to shrink suddenly, what would happen to the length of the day?
Answer: When the earth shrinks, the moment of inertia  decreases about its own axis due to the decrease in radius R To conserve angular momentum.
decreases about its own axis due to the decrease in radius R To conserve angular momentum.
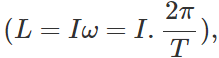 the time period T decreases. That is, the length of the day decreases.
the time period T decreases. That is, the length of the day decreases.
Q.70 A body A of mass M while falling vertically downwards under gravity breaks into two parts; a body B of mass M/ 3 and a body C of mass 2 M/ 3. How does the centre of mass of bodies B and C taken together shift compared to that of A?
Answer: The centre of mass of bodies B and C does not shift compared to body A. It continues to move vertically downwards under the effect of gravity. This is because there is no new external force acting on the system.
Q.71 Two identical particles move towards each other with velocity 2υ and υ respectively. What is the velocity of the centre of mass?
Answer: Here m1=m2=m; υ=2υ and υ2=−υ ∴ 
Q.72 A particle moves in a circular path with decreasing speed. What happens to its angular momentum?
Answer: The angular momentum of a particle of mass m moving with velocity 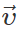 along a circular path of radius r is given by
along a circular path of radius r is given by 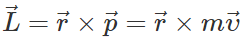 When the speed υ decreases, the magnitude of angular momentum decreases. But the direction of angular momentum remains unchanged.
When the speed υ decreases, the magnitude of angular momentum decreases. But the direction of angular momentum remains unchanged.
Q.73 A particle performing uniform circular motion has angular momentum L. What will be the new angular momentum, if its angular frequency is doubled and its kinetic energy halved?
Answer: Rotational K.E., K= 1/2 Iw2 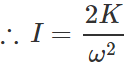 Angular momentum,
Angular momentum,
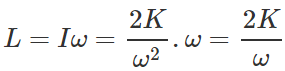 When angular frequency is doubled and kinetic energy is halved, the angular momentum becomes,
When angular frequency is doubled and kinetic energy is halved, the angular momentum becomes, 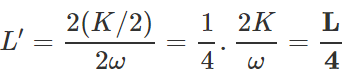
Q.74 The angular velocity of the earth around the sun increases, when it comes closer to the sun. Why?
Answer: When the earth comes closer to the sun, its moment of inertia about the axis through the sun decreases. To conserve angular momentum(L=Iω), the angular velocity of the earth increases.
Q.75 Why are we not able to rotate a wheel by pulling or pushing along its radius?
Answer: This is because radial component of the applied force cannot produce torque. τ = r F sinθ = 0 × Fsin θ = 0
Q.76 Two solid spheres of the same mass are made of metals of different densities. Which of them has larger moment of inertia about its diameter?
Answer: The sphere of metal with smaller density, will have larger size and hence it will have larger moment of inertia than the other sphere.
Q.77 A planet revolves around a massive star in a highly elliptical orbit. Is the angular momentum constant over the entire orbit?
Answer: A planet revolves around a star under the effect of the gravitational force, which is purely radial in nature. As radial component of a force does not contribute to torque, so the angular momentum of the planet remains unaffected. As τ=dL/dt=0, so L=constant.
Q.78 If no external torque acts on a body, will its angular velocity remain constant? Give reason.
Answer: When no external torque acts on a body, its angular momentum remains constant. But L=Iω Clearly, the angular velocity ω will remain constant only so long as the moment of inertia I of the body remains constant.
Q.79 "Newton's laws of motion are applicable to individual particles". How would you explain the motion of a large body?
Answer: A large body can be considered as made of a number of mass particles and all mass particles interact with each other. The vector sum of all these internal forces is zero. Therefore for a large body, it can be replaced by a single mass particle whose mass is supposed to be situated at its centre of mass and the Newton's laws can be applied.
Q.80 If an external force can change the state of motion of CM of a body, how does the internal force of the brakes bring a car to rest?
Answer: Actually, it is not the external force which brings the car to rest. The internal force of the brakes on the wheel locks the wheel. Now a large frictional force comes into play between the wheels and the grounds. This force is external to the system and brings the car to rest.
Q.81 Two men stand facing each other on two boats floating on still water at a distance apart. A rope is held at its ends by both. The two boats are found to meet always at the same point, whether each man pulls separately or both pull together, why? Will the time taken be different in the two cases? Neglect friction.
Answer: The men on the two boats floating on water constitute a single system. So the forces applied by the two men are internal forces. Whether each man pulls separately or both pull together, the centre of mass of the system of boats remains fixed due to the absence of any external force. Consequently, the two boats meet at a fixed point, which is the centre of mass of the system.
Q.82 What is the difference between centre of gravity and centre of mass?
Answer: Centre of mass is a point at which whole of the mass of the body may be assumed to be concentrated to describe its motion as a particle. Centre of gravity is a point at which resultant of the gravitational forces on all particles of the body acts. For bodies of normal dimensions, centre of mass and centre of gravity coincide. But centre of mass and centre of gravity relate to two different concepts. Even if the world were devoid of gravitational force, the centre of mass would still have a meaning.
Q.83 There are 100 passengers in a stationary railway compartment. A physical fight starts between the passengers over some difference of opinion, (i) Will the position of CM of the compartment change? (ii) Will the position of CM of system (compartment +100 passengers) change? Give reason.
Answer: (i) The position of the CM of the compartment will change because the passengers are external bodies for the compartment. (ii) The position of CM of the system will not change as no external force is acting on the system.
Q.84 Torque and work are both equal to force times distance. Then how do they differ?
Answer: (i) Work is a scalar quantity while torque is a vector quantity. (ii) Work is measured as the product of the applied force and the distance moved by the body in the direction of the force. Torque is measured as the product of the force and its perpendicular distance from the axis of rotation.
Q.85 When is a rigid body said to be in equilibrium? State the necessary conditions for a body to be in equilibrium.
Answer: A rigid body is said to be in equilibrium when its linear acceleration and angular acceleration are zero. (i) For translation equilibrium of a rigid body, the sum of all the external forces acting on it must be zero 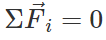 (ii) For rotational equilibrium of a rigid body, the sum of torques due to all forces acting on it must be zero.
(ii) For rotational equilibrium of a rigid body, the sum of torques due to all forces acting on it must be zero. 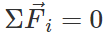
Q.86 Define moment of inertia. On what factors does it depend?
Answer: The moment of inertia of a rigid body about' an axis is the sum of the products of the masses of its various particles and squares of their perpendicular distances from the axis of rotation. I=Σmir2i The moment of inertia of a body depends on:-
(i) Mass of the body.
(ii) Size and shape of the body.
(iii) Distribution of mass about the axis of rotation.
(iv) Position and orientation of the axis of rotation with respect to the body.
Q.87 How will you distinguish between a hard boiled egg and a raw egg by spinning it on a table top?
Answer: Hard boiled egg acts just like a rigid body while rotating while it is not the case in a raw egg because of liquid matter present in it. In case of a raw egg, the liquid matter tries to go away from the centre, thereby increasing its moment of inertia. As moment of inertia is more the raw egg will spin with less angular acceleration provided same torque is applied in both the cases. Thus, hard boiled egg will spin faster.
Q.88 If two circular discs of the same mass and thickness are made from metals of different densities, which disc will have the larger moment of inertia about its central axis ? Explain.
Answer: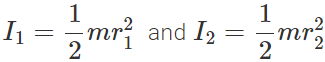
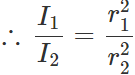 Also
Also 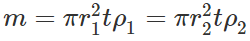
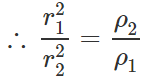 Hence
Hence 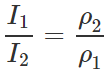 i.e., I∝1/ρ Thus the disc with greater density will have less moment of inertia.
i.e., I∝1/ρ Thus the disc with greater density will have less moment of inertia.
Q.89 Which one is easier to turn-a log or a bench of equal weight and length? The two have the same coefficient of friction with the ground. Explain.
Answer: In the case of a log, the force of friction is distributed along its entire length and so it is effective midway between the end where the force is applied and the centre of the log, but in the case of a bench, the force of friction is at the end. So to turn the log, the torque required is equal to μ mg l/2,, while to turn the bench, the torque required is equal to μ mgl. Hence it is easier to turn a log than a bench of equal weight and length.
Q.90 What is the moment of inertia of a rod of mass M, length l about an axis perpendicular to it through one end? Given the moment of inertia about the centre of mass is 1/12 Ml2
Answer: By using theorem of parallel axes, 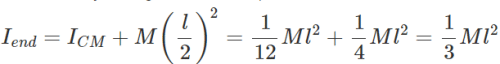
Q.91 What is the moment of inertia of a uniform circular disc of radius R and mass M about an axis passing through its centre and normal to the disc? The moment of inertia of the disc about any of its diameters is given to be(1 / 4) MR2.
Answer: M.I. of the disc about any diameter, ID=1/4MR2. By the theorem of perpendicular axes, M.I of the disc about an axis through the centre and normal to disc = M.I about any diameter+M.I about perpendicular diameter 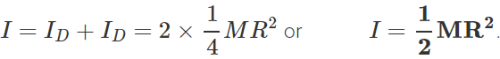
Q.92 The moment of inertia of a solid sphere about a tangent is 5/3 MR2, where M is mass and R is radius of the sphere. Find the M.I. of the sphere about its diameter.
Answer: Here IT=5/3 MR2 Now diameter of sphere is an axis passing through its centre of mass. By using theorem of parallel axes, IT=ICM+MR2 ∴
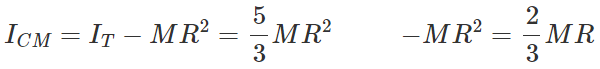
Q.93 The moment of inertia of a uniform circular disc about a tangent in its own plane is 5/4 MR2, where M is mass and R is the radius of the disc. Find its moment of inertia about an axis through its centre and perpendicular to its plane.
Answer: If ID is the M.I. of the disc about its diameter, then from the theorem of parallel axes, IT=ID+MR2 or ID=IT−MR2=5/4 MR2 −MR2=1/4 MR2 By the theorem of perpendicular axes, the M.I. about an axis through the centre and perpendicular to the plane of the disc, I= Sum of moments of inertia about two perpendicular diameters =ID+ID=2×1/4 MR2 or I=1/2 MR2.
Q.94 Using expressions for power and kinetic energy of rotational motion, derive the relation. τ=Iα,, where letters have their usual meanings.
Answer: Power in rotational motion, P=τω Rotational K.E., K=1/2 Iω2 Work done in rotational motion, W=Energy stored as rotational K.E. =1/2 Iω2 ∴ 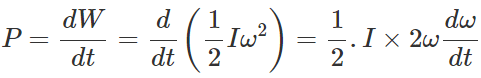 or τω=Iωα
or τω=Iωα
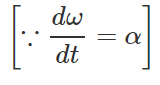 ∴ τ=Iα.
∴ τ=Iα.
Q.95 Explain if the ice on the polar caps of the earth melts, how will it affect the duration of the day?
Answer: If the ice on the polar caps of the earth melts, the water so formed will spread on the surface of earth. This increases the moment of inertia (I) of the earth about its own axis (due to change in the distribution of mass of the particles of water going away from the axis of rotation). To conserve angular momentum (=Iω), co (angular velocity of earth about its own axis) will decrease. As T=2π/ω,, hence due to decrease in the value of ω, T i.e., the duration of the day will increase.
Q.96 Two identical cylinders 'run a race' starting from rest at the top of an inclined plane, one slides without rolling and other rolls without slipping. Assuming that no mechanical energy is dissipated as heat, which one will win?
Answer: When the cylinder slides without rolling, E=1/2mυ′2 ∴
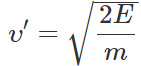 When the cylinder rolls without slipping,
When the cylinder rolls without slipping,
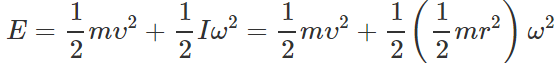
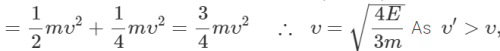 therefore sliding cylinder will win the race.
therefore sliding cylinder will win the race.
|
209 videos|261 docs|191 tests
|
FAQs on Short & Long Answer Questions: Systems of Particles & Rotational Motion - Physics for EmSAT Achieve
| 1. What are systems of particles in rotational motion? |  |
| 2. How is the moment of inertia calculated for a system of particles? |  |
| 3. What is the difference between rotational motion and translational motion? |  |
| 4. How does angular momentum relate to rotational motion? |  |
| 5. What are some real-life examples of systems of particles in rotational motion? |  |


















