Kinematics of Rotational Motion about a Fixed Axis | Physics for JEE Main & Advanced PDF Download

We all know that rotational motion and translational motion are analogous to each other. In rotational motion, the angular velocity is ω which is analogous to the linear velocity v in the transitional motion. Let us discuss further the kinematics of rotational motion about a fixed point.
The kinematic quantities in rotational motion like the angular displacement θ, angular velocity ω and angular acceleration α respectively corresponds to kinematic quantities in linear motion like displacement x, velocity v and acceleration a.

Angular Acceleration

The rate of change of angular velocity is the angular acceleration.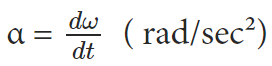

Now let us consider a particle P on a rotating object. The object undergoes a rotation motion at the fixed point. The angular displacement of a particle P is θ. Hence in time t = 0, the angular displacement of the particle P is 0. So we can say that in time t, its angular displacement will be equal to θ.

Angular Velocity

Angular velocity is the time rate of change of angular displacement. We can write it as,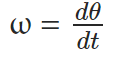

As we know that the rotational motion here is fixed, so there is no need to change the angular velocity. We know angular acceleration is α = dω/dt. So the kinematics equations of linear motion with uniform acceleration is,
v = v₀+ at 
x = x₀ + v₀t + 1/2 at² 
v² = v₀²+ 2ax 
Where  x₀  is the initial displacement and v₀ is the initial velocity of the particle. Here initial means t = 0. Now, this equation corresponds to the kinematics equation of the rotational motion. 

Kinematics Equations for Rotational Motion with Uniform Angular Acceleration

ω = ω₀+ αt 
θ = θ₀ + ω₀t + 1/2 αt² 
ω² =  ω₀² + 2α (θ – θ₀) 
Where θ₀  is the initial angular displacement of the rotating body and ω₀ is the initial angular velocity of the particle of the body.