Short & Long Answer Questions: Units & Measurement | Physics for JEE Main & Advanced PDF Download
Q.1. What is the necessity of selecting some units as fundamental units
Ans. The number of physical units required to be measured is very large. If a separate unit is defined for each of them, then it will become very difficult to remember all of them as they will be quite unrelated to each other.
Q.2. How is SI a coherent system of units?
Ans. In SI, all derived units can be obtained by multiplying and dividing the basic and supplementary units and no numerical factors are required to be introduced. So SI is a coherent system of units.
Q.3. In defining the standard of length, (the prototype metre), we have to specify the temperature at which the measurement should be made. Are we justified in calling length a fundamental quantity, if another physical quantity (temperature) has to be specified in choosing a standard?
Ans. Yes, the choice of length as a fundamental quantity is justified. The modem definition of metre in terms of wavelength of light radiation is not affected by temperature.
Q.4. Do Å and AU stand for the same unit of length?
Ans. No. 1 Å (angstrom) =10-10 m 1 AU (astronomical unit) = 1.496 × 1011 m.
Q.5. Why is it convenient to express the distances of stars in terms of light year rather than in metre or kilometre?
Ans. One light year = 9.46 × 1015 m = 9.46 × 1012 km. As the distances of stars are extra-ordinarily large, so it is convenient to express them in light year rather than in metre or kilometre.
Q.6. Comment on the statement: "To define a physical quantity for which no method of measurement is given or known has no meaning."
Ans. The given statement is not correct. A physical quantity, if it is called so, must have a physical meaning. If it cannot be measured by any direct method, these must be some indirect method for its measurement. Entropy is one such physical quantity.
Q.7. Is the measure of an angle dependent upon the unit of length?
Ans.
θ(radian) = (Arc/Radius)
As an angle is the ratio of the length of an arc and the radius i.e., it is the ratio of two lengths, so the measure of an angle does not depend upon the unit of length.
Q.8. What is meant by angular diameter of the moon? What is its value
Ans. The angle subtended by the two diametrically opposite ends of the moon at a point on the earth is called angular diameter of the moon. Its value is about 0.5∘.
Q.9. For a given base line, which will show a greater parallax - a distant star or a nearby star?
Ans. Parallactic angle, θ = (base line/distance of star) = b/S. Thus for a given base line b, parallax of a star is inversely proportional to its distance S. Hence the nearby star will show a greater parallax.
Q.10. Why is parallax method not useful for measuring the distances of stars more than 100 light years away?
Ans. For a star more than 100 light years away, the parallax angle is so small that it cannot be measured accurately.
Q.11. What is the difference between mN, Nm and nm?
Ans.
1 mN = 1 milli newton = 10-3 newton (unit of force).
1 Nm = 1 Newton metre (unit of work)
1 nm = 1 nanometre =10-9 metre (unit of distance).
Q.12. Do all physical quantities have dimensions? If no, name three physical quantities which are dimensionless.
Ans. No, all physical quantities do not have dimensions. The physical quantities like angle, strain and relative density are dimensionless.
Q.13. If 'slap' times speed equals power, what will be the dimensional equation for 'slap'?
Ans.
As slap x speed = power
Slap = (Power/Speed) = (ML2T-3/LT-1) = MLT-2
Q.14. What is the basis of the principle of homogeneity of dimensions
Ans. The principle of homogeneity of dimensions is based on the fact that only the physical quantities of the same kind can be added, subtracted or compared.
Q.15. If x = a + bt +ct2 where x is in metre and t in second; then what is the unit of c?
Ans.
[x] = [ct2]
or
[c] = [x/t2] Units of c = ms-2
Q.16. What are the dimensions of a and b in the relation: F =a+bx, where F is force and x is distance?
Ans.
[a] = [F] = MLT-2 [b] = [F/x] = (MLT-2/L) = MT-2
Q.17. Name two physical quantities having the dimensions [ML2T-2].
Ans. Work and torque.
Q.18. Write three physical quantities having dimensions [ML-1T-1]
Ans. Pressure, stress and Young's modulus of elasticity.
Q.19. If the units of force and length each are doubled, then how many times would the unit of energy be affected?
Ans. Energy = Work done = Force × length So when the units of force and length each are doubled, the unit of energy will increase four times.
Q.20. The velocity v of a particle depends on time t as: υ=At2 + Bt + C where v is in m/s and t in second. What are the units of A, B and C?
Ans.
Unit of
A = (Unit of v/Unit of t2) = ms-1/s2 = ms-3
Units of
B = (Unit of v/Unit of t) = ms-1/s = ms-2
Unit of
C = Unit of v = ms-1.
Q.21. Can a quantity have dimensions but still has no units?
Ans. No, a quantity having dimensions must have some units of its measurement.
Q.22. Can a quantity have different dimensions in different systems of units?
Ans. No, a quantity has same dimensions in all system of units.
Q.23. Can a quantity have units but still be dimensionless?
Ans. Yes. For example, a plane angle has no dimensions but has unit like radian for its measurement.
Q.24. Does the magnitude of a physical quantity depend on the system of units chosen?
Ans. No. The magnitude of physical quantity remains same in all systems of units.
Q.25. Justify L + L = L and L - L = L.
Ans. When we add a length to another length, we get length only so L + L = L is justified. When we subtract a length from another length, again we get length. This justifies L − L = L
Q.26. Can there be a physical quantity that has no units and no dimensions?
Ans. Yes, strain is a physical quantity that has no units and no dimensions.
Q.27. Can an instrument be called precise with-out being accurate? Can it be accurate without being precise?
Ans. Yes, an instrument can be precise without being accurate but the measurements cannot be accurate without being precise.
Q.28. Which of the following length measurements is
(i) most precise and
(ii) least precise?
Give reason
(i) l = 5 cm
(ii) l = 5.00 cm
(iii) 5.000 cm
(iv) 5.000 cm
(v) 5.00000 cm.
Ans.
(i) The last measurement is most precise, because it has been taken with an instrument whose least count is equal to 0.00001 cm.
(ii) The first measurement is least precise because it has been taken with a device having least count equal to 1 cm.
Q.29. Which of the following readings is the most accurate:
(i) 5000 m
(ii) 5×102 m
(iii) 5×103 m
Ans.
(i) 5000 m is most accurate.
Q.30. Which quantity in a given formula should be measured most accurately?
Ans. The quantity which has maximum power (say, n) in the formula should be measured more accurately because an error in measurement is multiplied n times in the final result.
Q.31. Which of the following measurements is more accurate and why?
(a) 0.0002 g
(b) 20.0 g
Ans. The measurement (a) 0.0002 g is more accurate because it is correct up to fourth decimal place while measurement (b) 20.0 g is correct up to first decimal place.
Q.32. Why do we treat length, mass and time as basic or fundamental quantities in mechanics?
Ans. In mechanics, the quantities like length, mass and time are taken as fundamental quantities because:
(i) These quantities represent basic scientific notations,
(ii) There is no other quantity simpler to them,
(iii) Length, mass and time cannot be expressed in terms of one another, and
(iv) All other physical quantities in mechanics can be expressed in terms of these quantities.
Q.33. SI is a rational system of units while mks system is not so. Justify.
Ans. SI assigns only one unit to a particular physical quantity so it is a rational system. For example, all types of energies are measured in joule in SI. But in mks system, mechanical energy is measured in joule, heat energy in calorie and electrical energy in watt-hour. So mks system is not a rational system of units.
Q.34. Why it became necessary to redefine metre on atomic standard?
Ans. It became necessary to redefine metre on atomic standard because the prototype metre offered the following difficulties:
(i) It is difficult to preserve a metre bar.
(ii) It is difficult to produce replicas of metre bar for their use in different countries.
(iii) The techniques used for producing replicas are not of very high accuracy.
Q.35. What are the advantages of defining metre in terms of the wavelength of light radiation?
Ans. The advantages of defining metre in terms of wavelength of light radiation are as follows:
(i) It can be easily reproduced anywhere and at any time.
(ii) It is invariant in time and space.
(iii) It is unaffected by environmental conditions like temperature and pressure.
(iv) It has an high accuracy of 1 part in 109.
Q.36. Give reasons why is platinum iridium alloy used in making prototype metre and kilogram.
Ans. The reasons for making standard kilogram and metre from platinum-iridium alloy are as follows:
(i) The alloy is least affected by temperature variations.
(ii) It is non-corrosive and so does not wear out easily.
(iii) It is quite hard.
(iv) It does not change with time.
Q.37. What is the basic principle of alpha particle scattering method for estimating the size of the nucleus?
Ans. Both the α-particle and nucleus are positively charged. When an α-particle approaches a nucleus, its kinetic energy gradually changes into potential energy due to repulsive forces. At the distance of closest approach r0, the entire kinetic energy changes into potential energy. This concept can be used to calculate r0, which gives the order of the size of the nucleus.
Q.38. What is common between bar and torr?
Ans. Both bar and torr are the units of pressure.
1 bar = 1 atmospheric pressure = 760 mm of Hg column
1 torr = 1 mm of Hg column
∴ 1 bar = 760 torr.
Q.39. Distinguish between accuracy and precision.
Ans. By accuracy of a measurement we mean that the measured value of a physical quantity is as close to the true value as possible. On the other hand, a measurement is said to be precise, if same value of the quantity is obtained in each of the various measurements carried out with the given apparatus.
Q.40 For the determination of "g" using a simple pendulum, measurements of land T are required. Error in the measurement of which of these will have larger effect on the value of "g" thus obtained and why? What is done to minimize this error?
Ans. Time period of a simple pendulum, 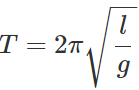
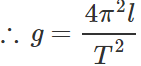
Clearly, the error in the measurement of time period T has larger effect on the value of g than the error in the measurement of length l.
Reasons
(i) T is very small.
(ii) In contrast to l, = T2 appears in the formula for g. To minimise the error, time period for a large number of oscillations is measured.
Q.41. Magnitude of force F experienced by a certain object moving with speed υ is given by F=Kv2 , where K is a constant. Find the dimensions of K.
Ans.
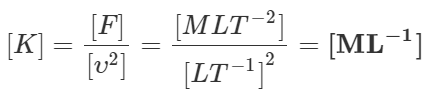
Q.42. Using the principle of homogeneity of dimensions, find which of the following is correct :
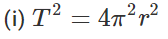
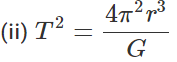
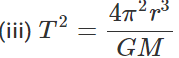
where T is time period, G is gravitational constant, M is mass and r is radius of orbit.
Ans.
(i) T2 = 4π2r2 Dimensionally, M0L0T2 = M0L2T0
As LHS ≠RHS, the formula is incorrect.
(ii)
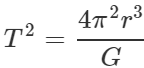
Dimensionally, m0L0T2
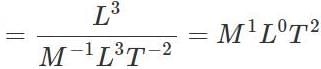

Dimensionally, m0L0T2

Q.43 The mean value of period of oscillation of a simple pendulum in an experiment is 2.825 s. The arithmetic mean of all the absolute errors is 0.11 s. Round off the period of simple pendulum to appropriate number of significant figures. Give reasons.
Ans. The absolute error 0.11 s has only two significant figures.
∴ Period of simple pendulum = 2.9 s [Rounded off up to 2 significant figures]
|
268 videos|740 docs|171 tests
|
FAQs on Short & Long Answer Questions: Units & Measurement - Physics for JEE Main & Advanced
| 1. What is the SI unit for measuring length? |  |
| 2. How can I convert centimeters to meters? |  |
| 3. What is the difference between mass and weight? |  |
| 4. How can I convert kilometers per hour to meters per second? |  |
| 5. What are some common units used to measure time? |  |

















