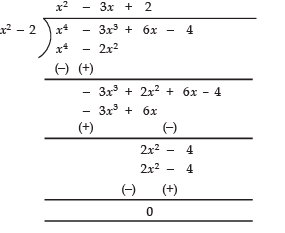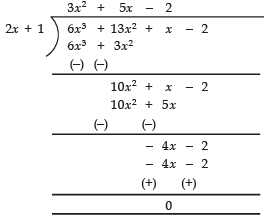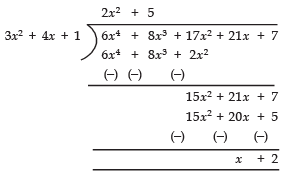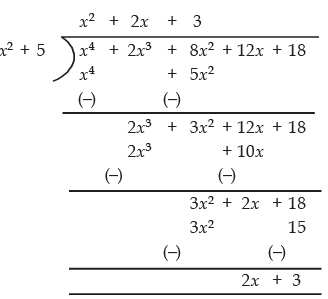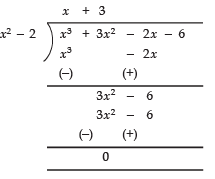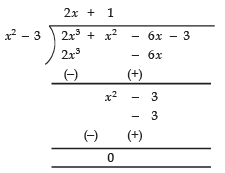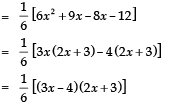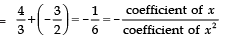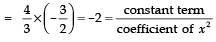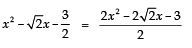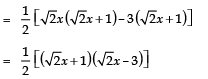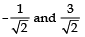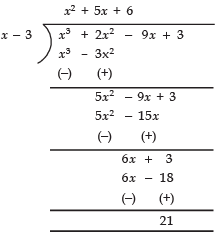Class 10 Maths Chapter 2 Question Answers - Polynomials - 1
Q1: Find the sum and product of zeroes of 3x2 - 5x + 6.
Here, p (x) = 3x2 - 5x + 6
Comparing it with ax2 + bx + c, we have
a = 3, b = - 5, c = 6
∴ Sum of the zeroes =
and, Product of the zeroes =
Q2: Find the sum and product of the zeroes of polynomial p (x) = 2x3 - 5x2 - 14x + 8.
Comparing p (x) = 2x3 - 5x2 - 14x + 8 with ax3 + bx2 + cx + d, we have
a = 2, b = –5,
c = - 14 and d = 8
∴ Sum of the zeroes =
Product of zeroes
Q3: Find a Quadratic polynomial whose zeroes are  .
.
Sum of zeroes (S)
Product of roots (P)
Since the required Quadratic polynomial
= k(x2 - Sx + P) ; where k is any real number.= k
Thus, the required polynomial is
= k (x2 - 2x - 1/4)
Q4: If α and β are the zeroes of a Quadratic polynomial x2 + x - 2 then find the value of  .
.
Comparing x2 + x - 2 with ax2 + bx + c, we have:
a = 1, b = 1, c = - 2
Thus,
Q5: If a and b are the zeroes of x2 + px + q then find the value of  .
.
Comparing x2 + px + q with ax2 + bx + c
a =1, b = p and c = q
∴ Sum of zeroes, a + b = - b/a
⇒
and αβ = c/a
⇒ αβ = q/1 = q
Now,Thus, the value of
is
Q6: Find the zeroes of the quadratic polynomial 6x2 - 3 - 7x.
We have,
= 6x2 - 3 - 7x = 6x2 - 7x - 3
= 6x2 - 9x + 2x - 3
= 3x (2x - 3) + 1 (2x - 3)
= (3x + 1) (2x - 3)
For 6x2 - 3 - 7x to be equal to zero,
either (3x + 1) = 0 or (2x - 3) = 0
⇒ 3x = - 1 or 2x = 3
⇒
Thus, the zeroes ofand 3/2.
Q7: Find the zeroes of 2x2 - 8x + 6.
We have,
2x2 - 8x + 6 = 2x2 - 6x - 2x + 6
= 2x (x - 3) - 2 (x - 3)
= (2x - 2) (x - 3)
= 2 (x - 1) (x - 3)
For 2x2 - 8x + 6 to be zero,
Either, x - 1 = 0 ⇒ x = 1
or x - 3 = 0 ⇒ x = 3
∴ The zeroes of 2x2 - 8x + 6 are 1 and 3.
Q8: Find the zeroes of the quadratic polynomial 3x2 + 5x - 2.
We have,
p (x) = 3x2 + 5x - 2
= 3x2 + 6x - x - 2
= 3x (x + 2) - 1 (x + 2)
= (x + 2) (3x - 1)
For p (x) = 0, we get
Either x + 2 = 0 ⇒ x = - 2
or 3x - 1 = 0 ⇒ x = 1/3
Thus, the zeroes of 3x2 + 5x - 2 are - 2 and 1/3.
Q9: If the zero of a polynomial p (x) = 3x2 - px + 2 and g (x) = 4x2 - q x - 10 is 2, then find the value of p and q.
∵ p (x) = 3x2 - px + 2
∴ p (2) = 3 (2)2 - p (2) + 2 = 0
[2 is a zero of p (x)]
or 12 - 2p + 2 or 14 - 2p = 0
or p = 7
Next g (x) = 4x2 - q x - 10
∴ g (2) = 4(2)2 - Q (2) - 10 = 0
[2 is a zero of g (x)]
or 4 × 4 - 2q - 10 = 0
or 16 - 2q - 10 = 0
or 6 - 2q = 0
⇒ q = 6/2 ⇒ q = 3
Thus, the required values are p = 7 and q = 3.
Q10: Find the value of ‘k’ such that the quadratic polynomial 3x2 + 2kx + x - k - 5 has the sum of zeroes as half of their product.
Here, p (x) = 3x2 + 2kx + x - k - 5
= 3x2 + (2k + 1) x - (k + 5)
Comparing p (x) with ax2 + bx + c, we have:
a = 3, b = (2k + 1),
c = - (k + 5)
∴ Sum of the zeroes
Product of the zeroes
According to the condition,
Sum of zeroes = 1/2 (product of roots)
⇒ - 2 (2k + 1) = - (k + 5)
⇒ 2 (2k + 1) = k + 5
⇒ 4k + 2 = k + 5
⇒ 4k - k = 5 - 2
⇒ 3k = 3
⇒ k = 3/3 = 1
Q11: On dividing p (x) by a polynomial x - 1 - x2, the Quotient and remainder were (x - 2) and 3 respectively. Find p (x).
Here,dividend = p (x)
Divisor, g (x) = (x - 1 - x2)
Quotient, q(x) = (x - 2)
Remainder, r (x) = 3
∵ Dividend = [Divisor × Quotient] +Remainder
∴ p (x)= [g (x) × q(x)] + r (x)
= [(x - 1 - x2) (x - 2)] + 3
= [x2 - x - x3 - 2x + 2 + 2x2] + 3
= 3x2 - 3x - x3 + 2 + 3
= - x3 + 3x2 - 3x + 5
Q12: Find the zeroes of the polynomial f (x) = 2 - x2.
We have f (x)= 2 - x2
= (√2 )2 - x2
Q13: Find the cubic polynomial whose zeroes are 5, 3 and - 2.
∵ 5, 3 and - 2 are zeroes of p (x)
∴ (x - 5), (x - 3) and (x + 2) are the factors of p (x)
⇒ p (x) = k (x - 5) (x - 3) (x + 2)
= k (x2 - 8x + 15) (x + 2)
= k (x3 - 8x2 + 15x + 2x2 - 16x + 30
= k (x3 + [- 8 + 2] x2 + [15 - 16] x + 30)
= k (x3 - 6x2 - x + 30)
Thus, the required polynomial is k (x3 - 6x2 - x + 30).
Q14: If α, β and γ be the zeroes of a polynomial p (x) such that (α + β +γ) = 3, (αβ + βγ + γα) = -10 and αβγ = - 24 then find p (x).
Here, α + β + γ = 3
αb + βγ + γα = - 10
αβγ = - 24
∵ A cubic polynomial having zeroes as α,β,γ is
p (x) = x3 - (a + b + γ) x2 + (αβ + βγ + γα) x - (αβγ)
∴The required cubic polynomial is
= k {x3 - (3) x2 + (- 10) x - (- 24)}
= k(x3 - 3x2 - 10x + 24)Note: If α, β and γ be the zeroes of a cubic polynomial p (x) then
p (x) = x3 - [Sum of the zeroes] x2 + [Product of the zeroes taken two at a time] x - [Product of zeroes]
i.e., p (x) = k {x3 - (α + β + γ) x2 + [αβ + βγ + γα] x - (αβγ).
Q15: Find all the zeroes of the polynomial 4x4 - 20x3 + 23x2 + 5x - 6 if two of its zeroes are 2 and 3.
Here, p (x) =4x4 - 20x3 + 23x2 + 5x - 6
Since, 2 and 3 are the zeroes of p (x),
∴ (x - 2) and (x - 3) are the factors of p(x)
⇒ (x - 2) (x - 3) is a factor of p (x)
⇒ x2 - 5x + 6 is a factor of p (x)
Now, using the division algorithm for x2 - 5x + 6 and the given polynomial p (x), we
get:
∴ We get (x2 - 5x + 6) (4x2 - 1) = p (x)
⇒ (x - 3) (x - 2) [(2x)2 - (1)2] = p (x)
⇒ (x - 3) (x - 2) (2x - 1) (2x + 1) = p (x)
⇒
Thus, all the zeroes of p (x) are:
Q16: If 1 is a zero of x3 - 3x2 - x + 3 then find all other zeroes.
Here,p (x) = x3 - 3x2 - x + 3
∵ 1 is a zero of p (x)
∴ (x - 1) is a factor of p (x).
Now, dividing p (x) by (x - 1), we have:
∴ p (x) = (x - 1) (x2 - 2x - 3)
⇒ p (x) = (x - 1) [(x2 - 3x + x - 3)]
= (x - 1) [x (x - 3) + 1 (x - 3)]
= (x - 1) [(x - 3) (x + 1)]
i.e., (x - 1), (x - 3) and (x + 1) are the factors of p (x).
⇒ 1, 3, and - 1 are the zeroes of p (x).
Q17: Find all the zeroes of 2x4 - 3x3 - 3x2 + 6x - 2, if two of its zeroes are 1 and 1/2.
Here, p(x) = 2x4 - 3x3 - 3x2 + 6x - 2
∵ 1 and are the zeroes of p (x)
∴ (x - 1) andare the factors of p (x)
⇒ (x - 1) (2x - 1) is a factor of p (x)
⇒ (2x2 - 3x + 1) is a factor of p (x).
Now, dividing p (x) by 2x2 - 3x + 1, we get
∴ p (x) = (2x2 − 3x + 1) (x2 − 2)
are the zeroes of p (x).
Q18: On dividing 4x3 - 8x2 + 8x + 1 by a polynomial g (x), the Quotient and remainder were (2x2 - 3x + 2) and (x + 3) respectively. Find g(x).
∵ Dividend = Divisor × Quotient + Remainder
i.e., p (x) = g (x) × Q (x) + r (x)
∴ g (x) =
Thus, the required polynomial g (x) = 2x - 1.
Q19: If α and β are the zeroes of the quadratic polynomial p (x) = kx2 + 4x + 4 such that α2 + β2 = 24, find the value of k.
Here, p (x) = kx2 + 4x + 4.
Comparing it with ax2 + bx + c, we have:
a = k; b = 4; c = 4
∴ Sum of the zeroes = -b/a
⇒ α + β = -4/k
and Product of the zeroes = c/a
⇒ αβ = 4/k
∵ α2 + β2 = 24
∴ (α + β)2 - 2αβ = 24
[∵ (x + y)2 = x2 + y2 + 2xy ⇒ (x + y)2 - 2xy = x2 + y2]
⇒
⇒
⇒ 16 − 8k − 24k2 =0
⇒ 24k2 + 8k − 16 = 0
⇒ (3k − 2) (k + 1) = 0
⇒ 3k − 2= 0 or k + 1 = 0
⇒ k = 2/3 or k = -1
Q20: Find the zeroes of the quadratic polynomial 6x2 - 3 - 7x and verify the relationship between the zeroes and the coefficients of the polynomial.
Here, p (x) = 6x2 - 3 - 7x = 6x2 - 7x - 3
= 6x2 - 9x + 2x - 3
= 3x (2x - 3) + 1 (2x - 3)
= (2x - 3) (3x + 1)
=
∴ Zeroes of p (x) are 3/2 and
To verify the relationship:
Sum of the zeroes =⇒
⇒
⇒ 7/6 = 7/6
L.H.S = R.H.S ⇒ Relationship is verified.
Product of the zeroes =⇒
⇒
i.e., L.H.S = R.H.S ⇒ Relationship is verified.
Q21: Find the zeroes of the quadratic polynomial 5x2 - 4 - 8x and verify the relationship between the zeroes and the coefficients of the polynomial.
p (x) = 5x2 - 4 - 8x
= 5x2 - 8x - 4
= 5x2 - 10x + 2x - 4
= 5x (x - 2) + 2 (x - 2)
= (x - 2) (5x + 2)
∴ zeroes of p (x) are 2 and
Relationship Verification
Sum of the zeroes
⇒
⇒
⇒ 8/5 = 8/5i.e., L.H.S. = R.H.S. ⇒ relationship is verified.
Product of the zeroes =
⇒
⇒
i.e., L.H.S. = R.H.S.
⇒ The relationship is verified.
Q22: Find the quadratic polynomial, the sum of whose zeroes is 8 and their product is 12. Hence, find the zeroes of the polynomial.
The quadratic polynomial p (x) is given by
x2 - (Sum of the zeroes) x + (Product of the zeroes)
∴ The required polynomial is
= x2 - [8] x + [12]
= x2 - 8x + 12
To find zeroes:
∵ x2 - 8x + 12 = x2 - 6x - 2x + 12
= x (x - 6) - 2 (x - 6)
= (x - 6) (x - 2)
∴ The zeroes of p (x) are 6 and 2.
Q23: If one zero of the polynomial (a2 - 9) x2 + 13x + 6a is reciprocal of the other, find the value of ‘a’.
Here, p (x) = (a2 - 9) x2 + 13x + 6a
Comparing it with Ax2 + Bx + C, we have:
A = (a2 - 9); B = 13; C = 6
Let one of the zeroes = a
∴ The other zero = 1/α
Now, Product of the zeroes⇒
⇒ 6a = a2 − 9 ⇒ a2 − 6a + 9 = 0
⇒ (a − 3)2 =0 ⇒ a − 3=0
⇒ a = 3
Thus, the required value of a is 3.
Q24: If the product of zeroes of the polynomial ax2 - 6x - 6 is 4, find the value of ‘a’
Here, p (x) = ax2 - 6x - 6
∵ Product of zeroes =
but product of zeroes is given as 4
∴⇒ − 6 = 4 × a
⇒⇒
Thus, the required value of a is -3/2.
Q25: Find all the zeroes of the polynomial x4 + x3 - 34x2 - 4x + 120, if two of its zeroes are 2 and - 2.
Here p (x) = x4 + x3 - 34x2 - 4x + 120
∵ The two zeroes of p (x) are 2 and - 2
∴ (x - 2) and (x + 2) are factors of p (x)
⇒ (x - 2) (x + 2) is a factor of p (x)
⇒ x2 - 4 is a factor of p (x).
Now, dividing p(x) by x2 - 4, we have:
∵ Remainder = 0
∴ p (x) = (x2 - 4) (x2 + x - 30)
i.e., x2 + x - 30 is also a factor of p (x).
∵ x2 + x - 30 = x2 + 6x - 5x - 30 = x (x + 6) - 5 (x + 6)
= (x + 6) (x - 5) = [x - (- 6)] [x - 5]
- 6 and 5 are also zeroes of p (x).
⇒ All the zeroes of the given polynomial are : 2, - 2, 5 and - 6
Q26: Find all the zeroes of the polynomial 2x4 + 7x3 - 19x2 - 14x + 30, if two of its zeroes are √2 and -√2.
P(x) = 2x4 + 7x3 - 19x2 - 14x + 30
∵ √2 and -√2 are the two zeroes of p (x).
∴are the factors of p (x).
⇒i.e., x2 - 2 is a factor of p (x).
Now, dividing p (x) by x2 - 2, we have:
∴ p (x) = (2x2 + 7x - 15) (x2 - 2)
[∵ Remainder = 0]
⇒ 2x2 + 7x - 15 is a factor of p (x)
∵ 2x2 + 7x - 15 = 2x2 + 10x - 3x - 15
= 2x (x + 5) - 3 (x + 5)
= (2x - 3) (x + 5)
=
∴ 3/2 and - 5 are zeroes of p (x)are the zeroes of p (x).
Q27: Find the quadratic polynomial whose zeroes are 1 and - 3. Verify the relation between the coefficients and the zeroes of the polynomial.
The given zeroes are 1 and - 3.
∴ Sum of the zeroes = 1 + (- 3) = - 2
Product of the zeroes = 1 × (- 3) = - 3
A quadratic polynomial p (x) is given by
x2 - (sum of the zeroes) x + (product of the zeroes)
∴ The required polynomial is
x2 - (- 2) x + (- 3)
⇒ x2 + 2x - 3
Verification of relationship
∵ Sum of the zeroes∴
⇒− 2= − 2i.e., L.H.S = R.H.S ⇒ The sum of zeroes is verified
∵ Product of the zeroes =
∴
⇒− 3= − 3i.e., L.H.S = R.H.S ⇒ The product of zeroes is verified.
Q28: Find the zeroes of the quadratic polynomial 4x2 - 4x - 3 and verify the relation between the zeroes and its coefficients.
Here, p (x) = 4x2 - 4x - 3 = 4x2 - 6x + 2x - 3
= 2x (2x - 3) + 1 (2x - 3)
= (2x - 3) (2x + 1)
=
∴are zeroes of p (x).
Verification of relationship
∵ Sum of the zeroes =∴

⇒ 2/2 = 1 ⇒ 1= 1
⇒
2/2 = 1 ⇒ 1 = 1
i.e., L.H.S = R.H.S ⇒ Sum of zeroes is verified
Now, Product of zeroes =
⇒
i.e., L.H.S = R.H.S ⇒ Product of zeroes is verified.
Q29: Obtain all other zeroes of the polynomial 2x3 - 4x - x2 + 2, if two of its zeroes are √2 and -√2.
p (x) = 2x3 - 4x - x2 + 2
∵ √2 and -√2 are the zeroes of p (x)
∴and are the factors of p (x)
⇒is a factor of p (x)
⇒ x2 - 2 is a factor of p (x)
Now, Dividing p (x) by (x2 - 2), we have:⇒ p (x) = (x2 - 2) (2x - 1)
∴ 2x - 1 is also a factor of p (x)
i.e.,is another factor of px.
⇒ 1/2 is another zero of p (x)
Q30: Find all the zeroes of x4 - 3x3 + 6x - 4, if two of its zeroes are √2 and - √2.
p (x) = x4 - 3x3 + 6x - 4
∵ √2 and (- √2) are the zeroes of p(x)
∴ x-√2 and x-(- √2) are factors of p (x)
⇒is a factor of p (x).
⇒ x2 - 2 is a factor of p (x)
On Dividing p (x) by x2 - 2, we have:
Since, remainder = 0
∴ (x2 - 2) (x2 - 3x + 2) = p (x)
Now, x2 - 3x + 2 = x2 - 2x - x + 2
= x (x - 2) - 1 (x - 2) = (x - 1) (x - 2)
i.e., (x - 1) (x - 2) is a factor of p (x)
∴ 1 and 2 are zeroes of p (x).
∴ All the zeroes of p (x) are ,√2 , - √2, 1 and 2.
Q31: Find a quadratic polynomial whose zeroes are - 4 and 3 and verify the relationship between the zeroes and the coefficients.
We know that:
P (x) = x2 - [Sum of the zeroes] x + [Product of the zeroes] ...(1)
∵ The given zeroes are - 4 and 3
∴ Sum of the zeroes = (- 4) + 3 = - 1
Product of the zeroes = (- 4) × 3 = - 12
From (1), we have
x2 - (- 1) x + (- 12)
= x2 + x - 12 ...(2)
Comparing (2) with ax2 + bx + c, we have
a = 1, b = 1, c = - 12
∴ Sum of the zeroes = -b/a
⇒ (+ 3) + (- 4) = -1/1
i.e., L.H.S = R.H.S ⇒ Sum of zeroes is verified.
Product of zeroes = c/a
⇒ 3 × (- 4) = -12/1
⇒ - 12 = - 12
i.e., L.H.S = R.H.S ⇒ Product of roots is verified.
Q32: Using division algorithm, find the quotient and remainder on dividing f (x) by g (x), where f (x) = 6x3 + 13x2 + x - 2 and g (x) = 2x + 1
Here, f (x) = 6x3 + 13x2 + x - 2
g (x) = 2x + 1
Now, dividing f (x) by g (x), we have:
Thus, The quotient = 3x2 + 5x - 2
remainder = 0
Q33: If the polynomial 6x4 + 8x3 + 17x2 + 21x + 7 is divided by another polynomial 3x2 + 4x + 1 then the remainder comes out to be ax + b, find ‘a’ and ‘b’.
We have:
∴ Remainder = x + 2
Comparing x + 2 with ax + b, we have
a = 1 and b = 2
Thus, the required value of a = 1 and b = 2.
Q34: If the polynomial x4 + 2x3 + 8x2 + 12x + 18 is divided by another polynomial x2 + 5, the remainder comes out to be px + q. Find the values of p and q.
We have:
∴ Remainder = 2x + 3
Comparing 2x + 3 with px + q, we have
p = 2 and q = 3
Q35: Find all the zeroes of the polynomial x3 + 3x2 - 2x - 6, if two of its zeroes are - √2 and √2.
p (x) = x3 + 3x2 - 2x - 6
∵ Two of its zeroes are -√2 and √2
⇒is a factor of p (x)
⇒ x2 - 2 is a factor of p (x).
Now, dividing p (x) by x2 - 2 we have:∴ p (x) = (x2 - 2) (x + 3)
i.e., (x + 3) is a factor of p (x),
⇒ (- 3) is a zero of p (x)
∴All the zeroes of p (x) are - √2, √2 and - 3.
Q36: Find all the zeroes of the polynomial 2x3 + x2 - 6x - 3, if two of its zeroes are -√3 and √3.
p (x) = 2x3 + x2 - 6x - 3
Two of its zeroes are -√3 and √3
∴and are factors of p (x)
i.e.,is a factor of p (x)
⇒ x2 - 3 is a factor of p (x)
Now, Dividing p (x) by x2 - 3, we have:∴ p (x) = (x2 - 3) (2x + 1)
⇒is a factor of p (x)
⇒ -1/2 is a zero of p (x)
∴ All the zeroes of p (x) are -√3 , √3 and -1/2.
Q37: Find the zeroes of the polynomial 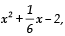 and verify the relation between the coefficients and the zeroes of the above polynomial.
and verify the relation between the coefficients and the zeroes of the above polynomial.
The given polynomial is
∴ zeroes of the given polynomial are
Now in,
co-efficient of x2 = 1
co-efficient of x = 1/6
constant term = –2
∴ Sum of zeroesProduct of zeroes
Q38: Find the quadratic polynomial, the sum and product of whose zeroes are  respectively. Also find its zeroes.
respectively. Also find its zeroes.
Sum of zeroes = √2
Product of zeroes
∵ A quadratic polynomial is given by
x2 – [sum of roots] x + [Product of roots]
∴ The required polynomial is
⇒
Since =
⇒ zeroes are
Q39: If the remainder on division of x3 + 2x2 + kx + 3 by x - 3 is 21, then find the quotient and the value of k. Hence, find the zeroes of the cubic polynomial x3 + 2x2 + kx - 18.
Let x3 + 2x2 + kx + 3 = p(x)
∵ The divisor = x – 3
∴ p(3) = 33 + 2 × 32 + 3k + 3
21 = 27 + 18 + 3k + 3
[∵ Remainder = 21]
⇒ 21 – 18 – 3 – 27 = 3k
⇒ –27 = 3k ⇒ k = – 9
Now, the given cubic polynomial
= x3 + 2x2 – 9x + 3
since,
∴ The required quotient = x2 + 5x + 6
Now, x3 + 2x2 – 9x – 18 = (x – 3) (x2 + 5x + 6)
= (x – 3) (x + 3) (x + 2)
⇒ The zeroes of x3 + 2x2 – 9x – 18 are 3, –3 and – 2
Q40: If a and b are zeroes of the quadratic polynomial x2 – 6x + a; find the value of ‘a’ if 3α + 2β = 20.
We have quadratic polynomial = x2 – 6x + a ...(1)
∵ a and b are zeroes of (1)
∴
It is given that: 3α + 2β = 20 ...(2)
Now, α +β = 6 ⇒ 2 (α+ β) = 2(6)
2α + 2β = 12 ...(3)
Subtracting (3) from (2), we have
Substituting a = 8 in α + β= 6, we get
8 +β = 6 ⇒ β = –2
Since, αβ = a
8(–2) = α ⇒ α = –16
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 2 Question Answers - Polynomials - 1
| 1. What is a polynomial? |  |
| 2. What are the different types of polynomials? |  |
| 3. How do you add and subtract polynomials? |  |
| 4. How do you multiply polynomials? |  |
| 5. What is the degree of a polynomial? |  |

|
Explore Courses for Class 10 exam
|

|











 and 3/2.
and 3/2.





 are the factors of p (x)
are the factors of p (x)

 are the zeroes of p (x).
are the zeroes of p (x).














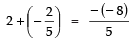
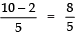
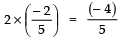
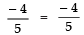
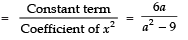
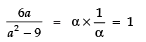
 ⇒ − 6 = 4 × a
⇒ − 6 = 4 × a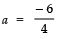 ⇒
⇒ 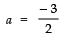
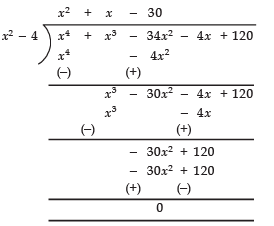
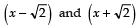 are the factors of p (x).
are the factors of p (x).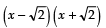 i.e., x2 - 2 is a factor of p (x).
i.e., x2 - 2 is a factor of p (x).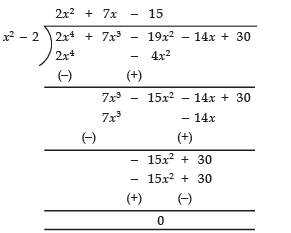
 are the zeroes of p (x).
are the zeroes of p (x).
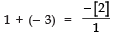
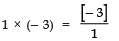
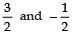 are zeroes of p (x).
are zeroes of p (x).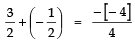
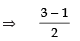


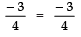
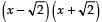 is a factor of p (x)
is a factor of p (x)