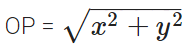Coordinate Geometry Class 10 Notes Maths Chapter 7
| Table of contents |

|
| Terminologies related to Cartesian Plane |

|
| Distance Formula |

|
| Section Formula |

|
| Finding Ratios given the Points |

|
| Mid Point of a Line Segment |

|
| Points of Trisection |

|
| Centroid of a Triangle |

|
Terminologies related to Cartesian Plane
- Position of a point P in the Cartesian plane with respect to co-ordinate axes is represented by the ordered pair (x, y).
- The line X’OX is called the X-axis and YOY’ is called the Y-axis.
- The part of intersection of the X-axis and Y-axis is called the origin O and the co-ordinates of O are (0, 0).
- The perpendicular distance of a point P from the Y-axis is the ‘x’ co-ordinate and is called the abscissa.
- The perpendicular distance of a point P from the X-axis is the ‘y’ co-ordinate and is called the ordinate.
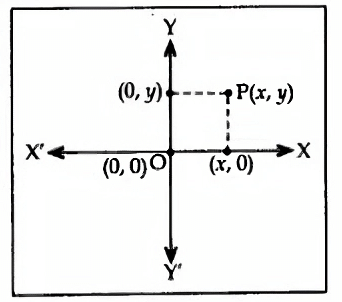
- Signs of abscissa and ordinate in different quadrants are as given in the diagram:
- Any point on the X-axis is of the form (x, 0).
- Any point on the Y-axis is of the form (0, y).
Distance Formula
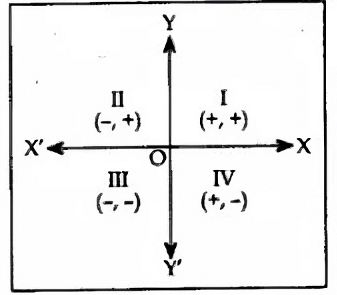
The distance between two points P(x1, y1) and Q (x2, y2) is given by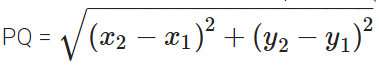
Note. If O is the origin, the distance of a point P(x, y) from the origin O(0, 0) is given by :
Example: Find the distance between the following points:
(i) (-1, 2) and (2, 3)
(ii) (0, 1) and (6, –1)
Solution:
(i) Let the distance between the points (-1, 2) and (2, 3) be d, then
d = √[(2 – ( –1))2 + (3 – 2)2] = √[9 + 1] = √10 units.
(ii) Let the distance between the points (0, 1) and (6, –1) be d, then
d = √[(6 – 0)2 + ( –1 – 1)2] = √[36 + 4] = √40 = 2√10 units.
Section Formula
The coordinates of the point which divides the line segment joining the points A(x1, y1) and B(x2, y2) internally in the ratio m : n are:
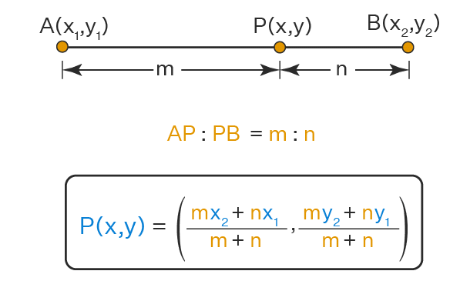
The above formula is section formula.
The ratio m: n can also be written as m/n : 1 or k:1, The co-ordinates of P can also be written as P(x, y) =
Example: Find the coordinates of the point which divides the line segment joining the points (4,6) and (-5,-4) internally in the ratio 3:2.
Sol: Let P(x, y) be the point which divides the line segment joining A(4, 6) and B(-5, -4) internally in the ratio 3 : 2.
Here,
(x1, y1) = (4, 6)
(x2, y2) = (-5, -4)
m : n = 3 : 2
Using the section formula,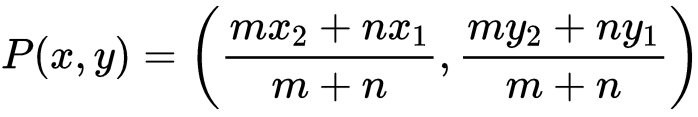
Coordinates of P are, 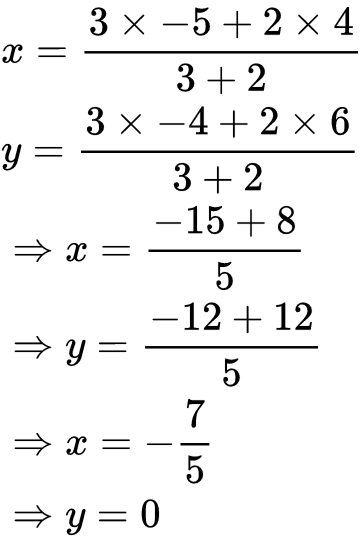
Therefore, P(x,y) = (-7/5,0).
Finding Ratios given the Points
To find the ratio in which a given point P(x, y) divides the line segment joining A(x1, y1) and B(x2, y2),
- Assume that the ratio is k : 1
- Substitute the ratio in the section formula for any of the coordinates to get the value of k.
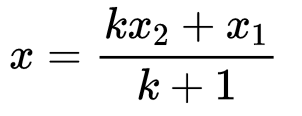 When x1, x2 and x are known, k can be calculated. The same can be calculated from the y- coordinate also.
When x1, x2 and x are known, k can be calculated. The same can be calculated from the y- coordinate also.
Example: Find the ratio when point (– 4, 6) divide the line segment joining the points A(– 6, 10) and B(3, – 8)?
Solution: Let the ratio be m:n.
We can write the ratio as:
m/n : 1 or k:1
Suppose (-4, 6) divide the line segment AB in k:1 ratio.
Now using the section formula, we have the following;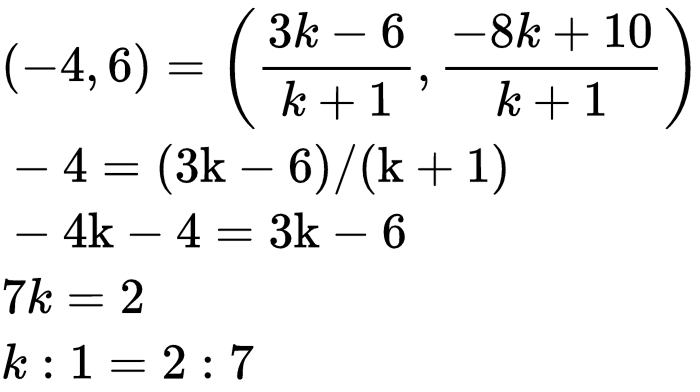
Thus, the required ratio is 2:7.
Mid Point of a Line Segment
The mid-point of the line segment joining the points P(x1, y1) and Q(x2, y2) is
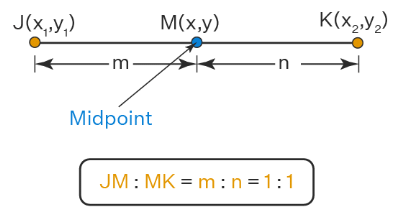
Substituting m = 1, n = 1 in section formula we get,
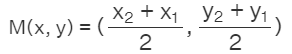
Points of Trisection
To find the points of trisection P and Q, which divides the line segment joining A(x1, y1) and B(x2, y2) into three equal parts:
i) AP : PB = 1 : 2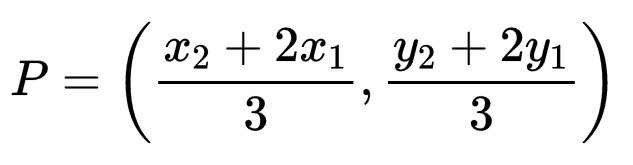
ii) AQ : QB = 2 : 1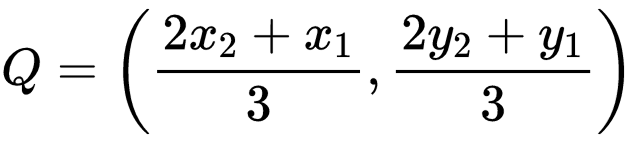
Example: Find the coordinates of the points of trisection of the line segment joining the points A(2, – 2) and B(– 7, 4).
Solution: Let P and Q divide the line segment AB into three parts.
So, P and Q are the points of trisection here.
Let P divides AB in 1:2, thus by section formula, the coordinates of P are (1, 0)
Let Q divides AB in 2:1 ratio, then by section formula, the coordinates are (-4,2)
Thus, the point of trisection for line segment AB are (1,0) and (-4,2).
Centroid of a Triangle
If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of a ΔABC, then the coordinates of its centroid(P) are given by: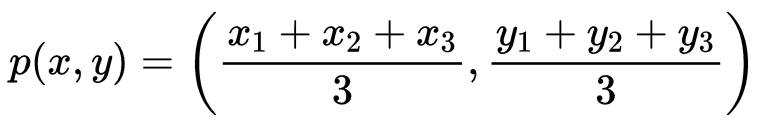
Example: Find the coordinates of the centroid of a triangle whose vertices are given as (-1, -3), (2, 1) and (8, -4)
Solution: Given,
The coordinates of the vertices of a triangle are (-1, -3), (2, 1) and (8, -4)
The Centroid of a triangle is given by:
G = ((x1+x2+x3)/3, (y1+y2+y3)/3)
G = ((-1+2+8)/3, (-3+1-4)/3)
G = (9/3, -6/3)
G = (3, -2)
Therefore, the centroid of a triangle, G = (3, -2)
|
127 videos|584 docs|79 tests
|
FAQs on Coordinate Geometry Class 10 Notes Maths Chapter 7
| 1. What is the Distance Formula and how is it derived? |  |
| 2. How do you use the Section Formula to find the coordinates of a point dividing a line segment? |  |
| 3. How do you find the midpoint of a line segment in the Cartesian Plane? |  |
| 4. What are the points of trisection of a line segment? |  |
| 5. How do you determine the centroid of a triangle using its vertices? |  |