Surface Area and Volumes Class 10 Notes Maths Chapter 12
Formulas for Surface Area and Volume of various Solids
Surface Area and Volume of Combinations
1. Cone on a Cylinder
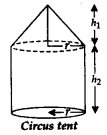
r = radius of cone & cylinder;
h1 = height of cone
h2 = height of cylinder
Total Surface area = Curved surface area of cone + Curved surface area of cylinder + area of circular base
= πrl + 2πrh2 +πr2;
Slant height, l =
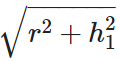
Total Volume = Volume of cone + Volume of cylinder
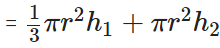
2. Cone on a Hemisphere
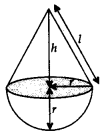
h = height of cone;
I = slant height of cone = 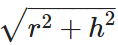
r = radius of cone and hemisphere
Total Surface area = Curved surface area of cone + Curved surface area of hemisphere = πrl + 2πr2
Volume = Volume of cone + Volume of hemisphere = 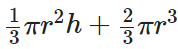
3. Conical Cavity in a Cylinder
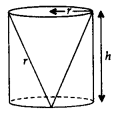 r = radius of cone and cylinder;
r = radius of cone and cylinder;
h = height of cylinder and conical cavity;
l = Slant height
Total Surface area = Curved surface area of cylinder + Area of the bottom face of cylinder + Curved surface area of cone = 2πrh + πr2 + πrl
Volume = Volume of cylinder – Volume of cone = 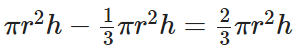
4. Cones on Either Side of the Cylinder
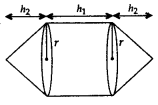 r = radius of cylinder and cone;
r = radius of cylinder and cone;
h1 = height of the cylinder
h2 = height of cones
Slant height of cone, l = 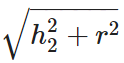
Surface area = Curved surface area of 2 cones + Curved surface area of cylinder = 2πrl + 2πrh1
Volume = 2(Volume of cone) + Volume of cylinder = 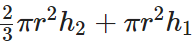
5. Cylinder with Hemispherical Ends
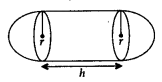 r = radius of cylinder and hemispherical ends;
r = radius of cylinder and hemispherical ends;
h = height of cylinder
Total surface area= Curved surface area of cylinder + Curved surface area of 2 hemispheres = 2πrh + 4πr2
Volume = Volume of cylinder + Volume of 2 hemispheres = πr2h+4/3πr3
6. Hemisphere on Cube or Hemispherical Cavity on Cube
a = side of cube;
r = radius of hemisphere.
Surface area = Surface area of cube – Area of hemisphere face + Curved surface area of hemisphere
= 6a2 – πr2 + 2πr2 = 6a2 + πr2
Volume = Volume of cube + Volume of hemisphere = 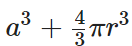
7. Hemispherical Cavity in a Cylinder
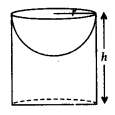 r = radius of hemisphere;
r = radius of hemisphere;
h = height of cylinder
Total surface area = Curved surface area of cylinder + Surface area of base + Curved surface area of hemisphere
= 2πrh + πr2 + 2πr2 = 2πrh + 3πr2
Volume = Volume of cylinder – Volume of hemisphere =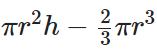
Some Solved Examples
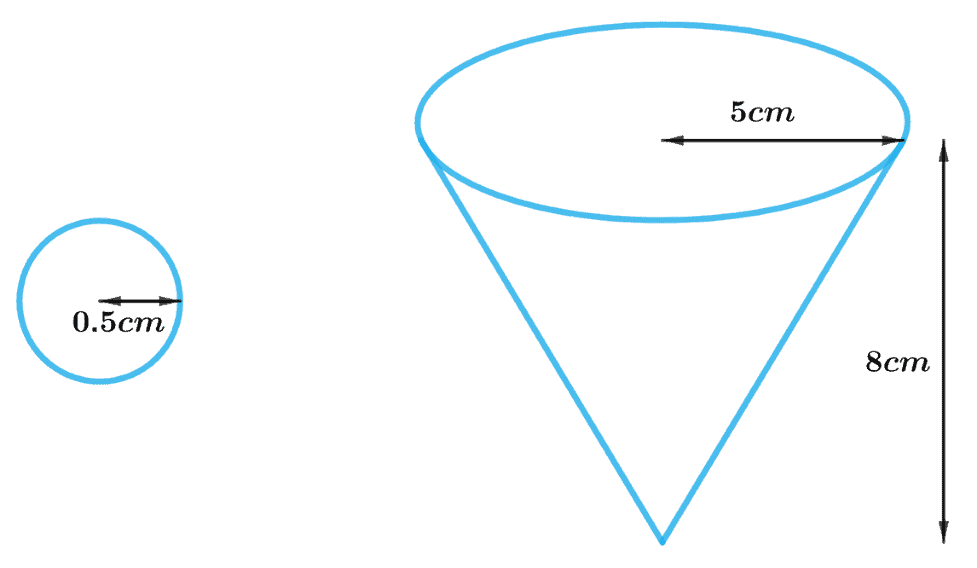
Example 1: A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Sol:
The figure drawn below of the vessel and lead shot is to visualize it.
As the water is filled up to the brim in the vessel
Volume of water in the vessel = Volume of the conical vessel
On dropping a certain number of lead shots (sphere) into the vessel one-fourth of the water flows out.
Volume of all lead shots dropped into the vessel = 1/4 × Volume of the water in the vessel
Hence,
Number of lead shots = 1/4 × volume of the water in the vessel ÷ volume of each lead shot
We will find the volume of the water in the vessel and lead shot by using formulae;
Volume of the sphere = 4/3 πr3
where r is the radius of the sphere
Volume of the cone = 1/3 πR2h
where R and h are the radius and height of the cone respectively
Height of the conical vessel, h = 8 cm
Radius of the conical vessel, R = 5 cm
Radius of the spherical lead shot, r = 0.5 cm
Number of lead shots = 1/4 × volume of the water in the vessel ÷ volume of each lead shot
= 1 /4 × (1/3) πR2h × 3/4 πr3
= πR2h/12 × 3/4πr3
= R2h / 16r3
= (5cm × 5 cm × 8 cm) / (16 × 0.5 cm × 0.5 cm × 0.5 cm)
= 100
Thus, the number of lead shots dropped in the vessel is 100.
Example 2: A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Sol:
The visualization of the solid figure is drawn below.
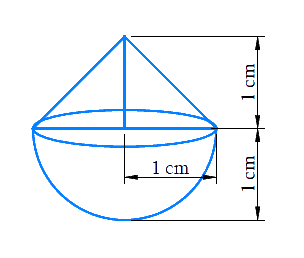
The volume of a solid is the space occupied inside it or the capacity that an object holds.
As the solid is made up of a conical part and a hemispherical part,
Volume of the solid = volume of the conical part + volume of the hemispherical part
Let us find the volume of the solid by using formulae;
Volume of the hemisphere = 2/3 πr3 where r is the radius of the hemisphere
Volume of the cone = 1/3 πr2h where r and h are the radius and height of the cone respectively.
Radius of hemispherical part = Radius of conical part = r = 1 cm
Height of conical part = h = r = 1 cm
Volume of the solid = volume of the conical part + volume of the hemispherical part
= 1/3 πr2h + 2/3 πr3
= 1/3 πr3 + 2/3 πr3 [Since, h = r]
= πr3
= π (1cm)3
= π cm3
Thus, the volume of the solid is π cm3.
|
126 videos|457 docs|75 tests
|


















