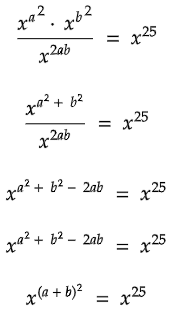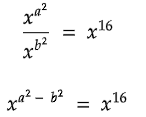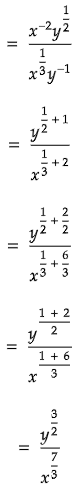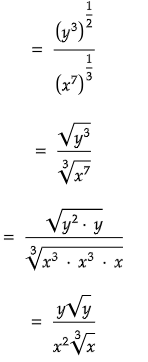Solved Examples: Exponents and Radicals | Mathematics for Digital SAT PDF Download

Clear all your SAT doubts with EduRev Join for Free

Join for Free

Q1: If 3^{x - 3} = 27, what is the value of x?
Solution:

In this question, we are trying to solve for the variable in exponent. In an equation, the idea to solve for the variable in exponent is to get the same base on both sides of the equation.

We have 27 on the right side of the given equation.

27 is a power of 3, that is 27 = 3³.

3^{x - 3} = 27

3^{x - 3} = 3³

In the equation, we have the same base on both sides. So, we can equate the exponents.

x - 3 = 3

Add 3 to both sides.

x = 6

Q2: If 9^x = 27⁸², what is the value of x?
Solution:

9^x = 27⁸²

(3²)^x = (3³)⁸² 

3^2x = 3²⁴⁶

2x = 246

Divide both sides by 2.

x = 123

Q3: If y⁸ = m and y⁹ = 2/3, what is the value of y in terms of m?
Solution:

y⁸ = m ----(1)

y⁹ = 2/3 

----(2)

Divide (2) by (1).

(2) ÷ (1) ----> y^m ÷ yⁿ = m ÷ (2/3)

y^{9 - 8} = m ⋅ (3/2)

y = 3m/2

Q4: k²x^2a = x^{2a + 2}
In the equation above, k, x and a are positive integers greater than 1. What is the value of x - k?
Solution:

k²x^2a = x^{2a + 2}

k²x^2a = x^2ax²

Divide both sides by x^2a.

k² = x²

Since both k and x are positive,

k = x

Therefore,

x - k = 0

Q5: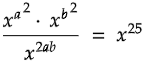
In the equation above, x > 1. Find the value of (a - b) such that (a - b) > 0. 
Solution:

(a + b)² = 25

Taking square root on both sides.

√(a + b)² = √25

a + b = ±5

a + b = 5  or  a + b = -5

Since (a + b) > 0,

a + b = 5

Q6: Which of the following is equal to ³√x² ⋅ √x³ ?
(a) x
(b) x^9/4
(c) x^13/6
(d) x³
Ans: (c)

³√x² ⋅ √x³ = (x²)^1/3 ⋅ (x³)^1/2

= x^2/3 ⋅ x^3/2

= x^{2/3 + 3/2}

= x^4/6 + 9/6

= x^{(4 + 9)/6}

= x^13/6

The correct answer choice is (c).

Q7: If 3√x³ = √72, what is the value of x?
Solution:

3√x³ = √72

√9√x³ = √72

√(9x³) = √72

Squaring both sides,

9x³ = 72

Divide both sides by 9.

x³ = 8

x³ = 2³

x = 2

Q8: If 3x - y = 12, what is the value of 8^x ÷ 2^y?
Solution:

8^x ÷ 2^y = (2³)^x ÷ 2^y

= 2^3x ÷ 2^y

= 2^{3x - y}

Substitute 3x - y = 12.

= 2¹²

Q9: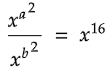
In the equation above, if x > 1 and a + b = 2, what is the value of (a - b)?
Solution:

a² - b² = 16

(a + b)(a - b) = 16

Substitute a + b = 2.

2(a - b) = 16

Divide both sides by 2.

a - b = 8

Q10: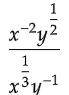
In the expression above x > 1 and y > 1. Which of the following is equivalent to the above expression ?
(a)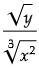
(b)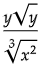
(c)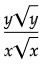
(d)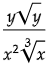

Ans: (d)

The correct answer choice is (d).