Solved Examples: Non Linear Equations | Mathematics for Digital SAT PDF Download

Clear all your SAT doubts with EduRev Join for Free

Join for Free

Example 1: f (x) = x² - 3
Complete the table below.

Sol:

Example 2: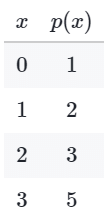

The table above shows the value of function p at several values of x.

Sol: According to the table, when x = 2, p(x) = 3. When x = 3, p(x) = 5.
As such, p(p(2)) = p(3) = 5.

Example 3: f(x) = x² + 3x + 7
g(x) = x³ 
The functions f and g are shown above. Which of the following expressions is equivalent to g(f(x))?
Sol: For g(f(x)), f is the inner function and g is the outer function. Therefore, we must replace each instance of x in the outer function with f(x): x² + 3x + 7.
f(x) = x² + 3x + 7
g(x) = x³
g(f(x)) = (x² + 3x + 7)³

Example 4: f(x) = -x² + 10
g(x) = f(x) -7
The functions f and g are shown above. For the same value of x, the value of g(x) is always greater than/less than/equal to the value of f(x).
Therefore, if the maximum value of the function f is 10, then the maximum value of function g is..........
Sol: g(x) is defined as f(x) - 7, which translates to 7 less than f(x). As such, for the same value of x, the value of g(x) is always 7 less than the value of f(x).
This means if the maximum value of the function f is 10, than the maximum value of function g must be 7 less than 10, or 10 - 7 = 3.

Example 5: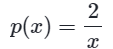
 
The function p is defined above. What is the value of p(2) + p(5) ?
Sol: We need to evaluate the function for both x = 2 and x = 5, then add the outputs.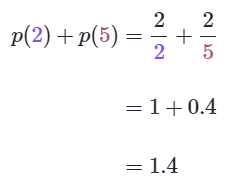

1.4 (or 7/5) is the value of p(2) + p (5).

Example 6: If f(x) = 3x + 5 and g(x) = x² - 4, what is the value of g(f(1)) ?
Sol: We need to input 1 into f, then use the output as the input for g.
First, let's evaluate f(1):
f(1) = 3(1) +5
= 3 + 5
= 8
Next, we need to input 8 into g to evaluate g(8):
9(8) = (8)2-4
= 64-4
= 60
60 is the value of g(f(1)).