Some Applications of Trigonometry Exercise 12.1(part-4) | Extra Documents, Videos & Tests for Class 10 PDF Download

Q56. A fire in a building B is reported on telephone to two fire station P and Q 2o km apart from each other on a straight road. P observes that the fire is at an angle of 60^∘ to the road and Q observes that it is at an angle of 45^∘ to the road. Which station sends its team and how much will this team have to travel?

Soln:

Let AB be the building

Angle of elevation from point P [fire station 1] α=60^∘

Angle of elevation from point Q [fire station 1] β=45^∘

Distance between fire station PQ = 20 km

The above data is represented in form of figure as shown

In right angle triangle if one of the included angle is Θ

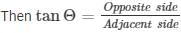
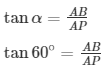
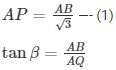
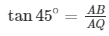
AQ = AB —- (2)

Adding (1) + (2)

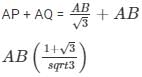
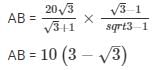
AQ = AB = 10(3−√3) = 12.64 km

Station 1 should send its team and they have to travel 7.32 km 

Q57.A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45^∘ and the angle of depression of the base is 30^∘ . Calculate the distance of the cliff from the ship and the height of the cliff.

Soln:

Height of the ship from water level = 10m = AB

Angle of elevation of top of the cliff α=45^∘

Angle of elevation of bottom of the cliff β=30^∘

Height of the cliff CD = ‘h’ m

Distance of the ship from foot of the tower cliff.

Height of cliff above ship be ‘a’ m

Then height of cliff = DX + XC = (10 + a) m

The above data is represented in form of figure as shown

In right angle triangle, if one of the included angle is Θ

AX = ‘a’m 

AX = 10√3

∴  a=10√3m

Height of the cliff = 10+10√3m=10(√3+1)

Q59.There are two temples one on each  bank of a river opposite to one other. One temple is 50m high. Form the top of this temple, the angles of depression of the top and foot of the other temple are 30^∘ and 60^∘ respectively. Find the width of the river and the height of the other temple.

Soln: 

Height of the temple 1 (AB) = 50m

Angle of depression of top of temple 2, α=30^∘

Angle of depression of bottom of temple 2, β=60^∘

Height of the temple 2 (CD) = ‘h’ m

Width of the river = BD = ‘x’ m

The above data is represented in from of figure as shown

In right angle triangle if one of the included angle is Θ

Here BD = CX, CD= BX 

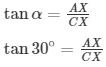
CX = A×√3m

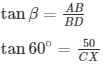
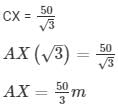
CD =XB = AB – AX =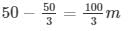 

Width of river = 50/√3

Height of temple 2 = 100/3 m

Q60.The angle of elevation of an airplane from a point on the ground is 45^∘. After a flight of 15 seconds, the elevation changes to 30^∘. If the airplane is flying at a height of 3000 meters, find the speed of the airplane.

Soln:

Let the airplane travelled from A to B in 15 sec

Angle of elevation of point A α=45^∘

Angle of elevation of point B β=30^∘

Height of the airplane from ground = 3000 meters

= AP = BQ

Distance travelled in 15 seconds = AB = PQ

Velocity (or) speed = distance travelled time

If the above data is represented is form of figure as shown

In right angle triangle if one of the included angle is Θ

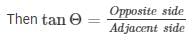
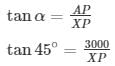
XP = 3000m 

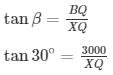
XQ =3000√3

PQ = XQ – XP = 3000(sqrt3−1)m

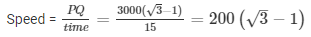
2000×0.732 

146.4 m/sec

Speed of the airplane = 146.4 m/sec

Q61.An airplane flying horizontally 1 km above the ground is observed at an elevation of 60^∘. After 10 seconds, its elevation is observed to be 30^∘. Find the speed of the airplane in km/hr.

Soln:

let airplane travelled from A to B in 10 seconds

Angle of elevation of point A α=60^∘

Angle of elevation of point B β=30^∘

Height of the airplane from ground = 1 km = AP = BQ

Distance travelled in 10 seconds = AB = PQ

The above data is represented in form of figure as shown

In right angle triangle if one of the included angle is Θ

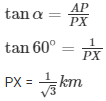
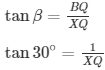
XQ =√3

PQ = XQ – PX =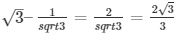

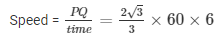
= 240√3

Speed of the airplane = 240√3

Q62.A tree standing on a horizontal plane is leaning towards east. At two points situated at distance a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is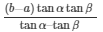 

Soln: 

AB be the tree leaning east

From distance ‘a’ m from tree, angle of elevation be α at point P.

From distance ‘b’ m from tree, angle of elevation be β at point Q.

The above data is represented in the form of figure as shown

In right angle triangle if one of the included angle is Θ

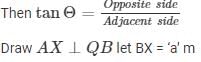
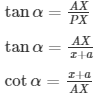
x+a = AXcotα —- (1)

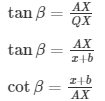
x+b = AXcotβ —- (2)

subtracting (1) from (2)

(x+b) – (x+a) = AXcot–AXcotα

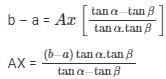
Height of top from ground =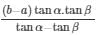 

Q63.The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15^∘ and the angle o0f depression of its reflection in the lake is 45^∘. What is the height of the cloud above the lake level?

Soln:

Let the cloud be at height PQ as represented from lake level

From point x, 2500 meters above the lake angle of elevation of top of cloud α=15^∘

Angle of depression of shadow reflection in water β=45^∘

Here above data is represented in form of figure as shown

In right angle triangle if one of the included angle is Θ

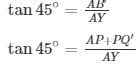
AY = x + (h + x)

AY = h + 2x —- (2)

From (1) and (2)

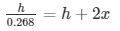
3.131h – h = 2 x 2500

h = 1830.8312

Height of the cloud above lake = h + x

= 1830.8312 + 2500

= 4330.8312 m

Q64.If the angle of elevation of a cloud from a point h meters above a lake is α and the angle of depression of its reflection in the lake be β, prove that the distance of the cloud from the point of observation is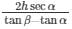 

Soln: 

let x be point ‘h’ meters above lake

Angle of elevation of cloud from x = α

Angle of depression of cloud reflection in lake = β

Height of the cloud from lake = PQ

PQ’ be the reflection then PQ’ = PQ

Draw XA + PQ, AQ = ‘x’ m, AP = ‘h’ m

Distance of cloud from point of observation is XQ.

The above data is represented in form of figure as shown

In ΔAQX

In ΔAXQ′

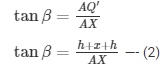
Subtracting (1) from (2) 

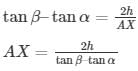
In ΔAQX

QX = AX sec α

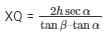
distance of cloud from point of observation =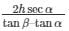 

Q65.From an airplane vertically above a straight horizontal road, the angle of depression of two consecutive mile stones on opposite side of the airplane are observed to be α and β. Show that the height in miles of airplane above the road is given by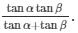

Soln: 

let PQ be the height of airplane from ground x and y be two mile stones on opposite side of the airplane xy = 1 mile

Angle of depression of x from p = α

Angle of depression of y from p = β

The above data is represented in the form of figure as shown

In right angle triangle if one of the included angle is Θ

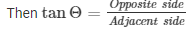
In ΔPXQ

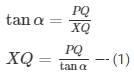
In ΔXQY

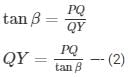
Adding (1) and (2) 

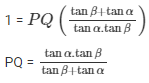
Height of airplane = 

Q66.PQ is a post given height ‘a’ m and AB is a tower at same distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.

Soln:

PQ is part height = ‘a’ m AB is tower height

Angle of elevation of B from P = α

Angle of elevation of B from Q = β

The above data is represented in gorm of figure as shown

In right angle triangle if one of the included angle is Θ

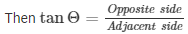
QX ⊥ AB, PQ = AK

In ΔABQ

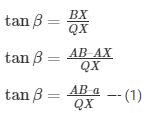
In ΔBPA

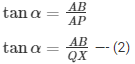
Dividing (1) by (2) 

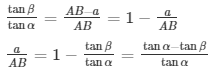
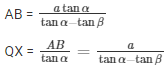
Height of tower =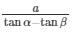 

Distance between post and tower =  

Q67.A ladder rest against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal. Show that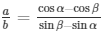

Soln: 

let AB be the ladder initially at an inclination α to ground

When its foot is pulled through distance ‘a’ let BB’ = ‘a’ m and AA’= ‘b’ m

New angle of elevation from B’ = B the above data is represented in form of figure as shown

Let AP⊥ groundB′P,AB=A′B′

A’P = x                  BP = y

In ΔABP

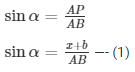
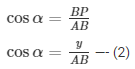
In ΔA′B′P

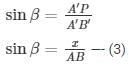
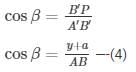
Subtracting (3) from (1) 

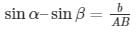
Subtracting (4) from (2) 

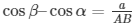
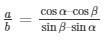
Q68.A tower subtends an angle α at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b meters just above A is β. Prove that the height of the tower is b tan α cot β.

Soln:

let height of the tower be ‘h’ m = PQ

Angle of elevation at point A on ground = α

Let B be the point ‘b’ m above the A

Angle of depression of foot of the tower from B = β

The above data is represented in form of figure as shown

Let BX ⊥ P,AB = A′B′

In ΔPBX

In ΔQBX

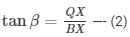
Dividing (1) by (2) 

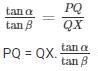 =b tan α.cot β

Q69.An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.

Soln:

Height of observer = AB = 1.5 m

Height of tower = PQ = 30 m

Height of tower above the observer eye = 30 – 1.5

QX = 28.5m

Distance between tower and observer XB = 28.5m

Θ be angle of elevation of tower top from eye

The above data is represented in the form of figure

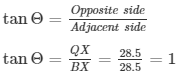
Θ=tan⁻¹(1)=45^∘ 

Angle of elevation = 45^∘

Q70. A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also each leg is inclined at an angle of 60^∘ to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distance.

Soln:

let AB be the height of stool = 1.5 m

Let P and Q be equal distance then AP = 0.5. AQ = 1 m

The above data is represented in form of figure as shown

BC = length of leg

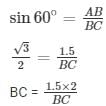
Draw PX ⊥ AB,QZ ⊥ AB,XY ⊥ CA,ZW ⊥ CA

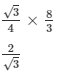
XC = 1.1077m 

CZ = 1.654m 

Q71.A boy is standing on the ground and flying a kite with 100m of string at an elevation of 30^∘. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45^∘. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the kites meet.

Soln:

For boy 1

Length of the string AB = 100 m

Angle made by string with ground = α=30^∘

For boy 2

Height of the building CD = 10m

Angle made by string with building top = β=45^∘

Length of the kite thread of boy 2 if both the kites meet must be ‘DB’

The above data is represented in form of figure as shown

Draw BX ⊥ AC,YD ⊥ BC

In ΔABX

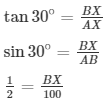
BX = 50m

BY = BX – XY = 50 – 10 = 40m

In ΔBYD

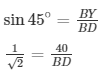
BD = 40√2

Length of thread or string of boy 2 = 40√2

Q72. From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h meters and the line joining the ships passes through the foot of the light house, show that the distance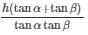

Soln: 

Height of light house = ‘h’ meters = AB

S₁ and S₂ be two ships on opposite sides of the light house

Angle of depression of S₁ from top of light house = α

Angle of depression of S₂ from top of light house = β

Required to prove that

Distance between ships = h(tanα+tanβ)/tanαtanβ  meters

The above data is represented in the form of figure as shown

In ΔABS₁

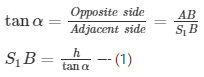
In ΔABS₂

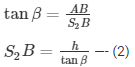
Adding (1) and (2) 

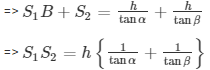
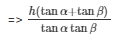
Distance between ships =