Some Special Parallelograms | Advance Learner Course: Mathematics (Maths) Class 7 PDF Download
Quadrilaterals can be defined as, types of polygons that have four sides, four vertices, and four angles along with a pair of diagonals. The Sum of interior angles of quadrilaterals is 360°. There are various kinds of quadrilaterals. As the name itself suggest the word is a combination of two Latin words ‘Quadri‘ means a variant of four, and ‘latus‘ means side. In this topic, we are going to study some special types of parallelogram like rectangle, square, rhombus.
A parallelogram is a special type of quadrilateral whose opposite side are equal and parallel.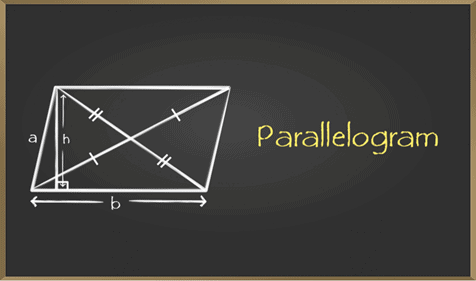
Properties of Parallelogram
There are different properties of parallelograms.
- Opposite sides are equal.
- Opposite angle are equal
- Diagonals bisect each other.
- A diagonal of a parallelogram divides it into two congruent triangles.
Some Special Parallelograms
Depending on the properties, there are three special types of parallelogram:
- Rectangle
- Rhombus
- Square
Rectangle
A rectangle is a special type of parallelogram which has all the properties of parallelogram along with some different properties. Each angle of a rectangle must be a right angle, i.e. of 90°. 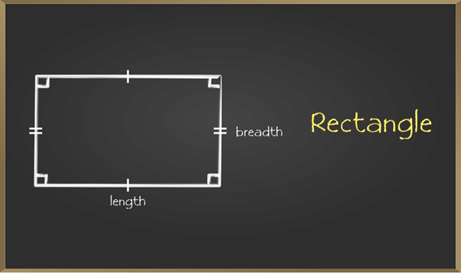
Properties of a Rectangle
Properties of a rectangle are similar to those of a parallelogram:
- Opposite Sides are parallel to each other.
- Opposite Sides of a rectangle are equal.
- Diagonals bisect each other
- Diagonals of the rectangle are equal.
- Each interior angle of a rectangle is equal i.e. 90°
Note: Rectangle has all the properties of parallelogram. So all rectangles are parallelogram but all parallelograms are not rectangle.
Sample Problems on Rectangles
Problem 1: In rectangle ABCD, AO = 5cm. Find the length of diagonal BD. Also find the perimeter of rectangle if AB = 8cm and AD = 6cm.
Solution:
AO = OC = 5cm (diagonals bisect each other)
Therefore, AC = 10cm
BD = AC =10cm (diagonals of rectangle are equal)
Perimeter = AB + BC + CD + DA
= 8 + 6 +8 +6 (opposite sides are equal)
= 28cm
Problem 2: In rectangle ABCD, ∠ABD = 3x – 7 and ∠CBA = 6x – 2. Find the value of x.
Solution:
Each angle of rectangle is 900
Therefore,
∠ABD + ∠CBA = 900
3x – 7 + 6x – 2 = 90
9x – 9 = 90
9x = 99
x = 11
Problem 3: In rectangle ABCD AO = 2x – 10 cm, OB = x + 4 cm. Find the length of diagonal BD
Solution:
In rectangle diagonals bisect each other and are equal.
Therefore, AO = OB
2x – 10 = x + 4
x = 14
OB = 14 + 4 = 18 cm
OD = 18 cm (as diagonals bisect each other)
Therefore, BD = 36 cm
Rhombus
A quadrilateral that has all sides equal and opposite sides parallel is called Rhombus. Opposite angles of a rhombus are equal and diagonals of the Rhombus bisect each other perpendicularly. Note all rhombus are parallelograms but the reverse of this is not true. 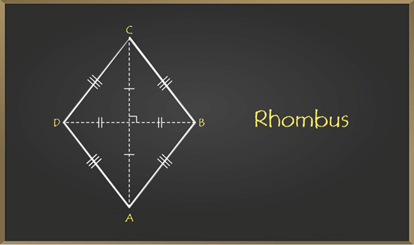
Properties of a Rhombus
Properties of a rhombus are similar to those of a parallelogram:
- Opposite Sides are parallel to each other.
- All the sides of a rhombus are equal to each other.
- Diagonals bisect each other
- Opposite angles of a rhombus are equal.
Note: Rhombus is a parallelogram with all side equal
Sample Problems on Rhombus
Problem 1: Diagonals of rhombus are 24cm and 10cm. Find the side of rhombus.
Solution:
AC = 24cm
BD = 10cm
Therefore, AO = 12cm and OB = 5cm (diagonals bisect each other)
In right-angled triangle AOB, (diagonals of rhombus are perpendicular)
AB2 = OA2 + OB2
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = 13cm
Therefore, side of rhombus is 13cm.
Problem 2: In a rhombus one of the diagonals is equal to a side of the rhombus. Find the angles of rhombus.
Solution:
In rhombus PQRS PR = PQ (given)
Therefore, PQ = QR = RS = SP = PR (as all side of rhombus are equal)
In triangle PQR
PQ = QR = PR
Therefore, it is an equilateral triangle.
∠QPR = ∠Q = ∠QRP = 600
||ly ∠SPR = ∠S = ∠PRS = 600
Therefore, angles of rhombus are ∠P = 1200 , ∠Q = 600, ∠R = 1200, ∠S = 600
Problem 3: Derive the formula for are of rhombus.
Solution:
As diagonals of rhombus bisect each other at right angle.
In rhombus ABCD
area of triangle ABD = 1/2 * BD *AO (1/2 * base *height) ………. (1)
area of triangle BCD = 1/2 * BD * CO ………………………………………….. (2)
Area of rhombus = Area of triangle ABD + area of triangle BCD
= 1/2 * BD * AO + 1/2 * BD * CO
= 1/2 * BD (AO + CO)
= 1/2 * BD * AC (AE + CE = AC)
Therefore, area of rhombus = 1/2 * product of diagonals
Square
A quadrilateral that has all sides equal and opposite sides parallel and all interior angles equal to 90° is called Square. Diagonals of a square bisect each other perpendicularly. Note that all squares are rhombus but not vice-versa.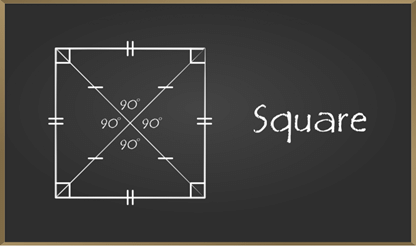
Properties of a Square
Properties of a square are similar to those of a rhombus:
- Opposite Sides are parallel to each other.
- All the sides of a square are equal to each other.
- Diagonals are perpendicular bisector of each other and are equal.
- All the angles of a square are equal and of 90° each.
Sample Problems on Square
Problem 1: All rhombus are squares or all squares are rhombus. Which of these statements is correct and why?
Solution:
Square and rhombus both have all sides equal but a rhombus is called square if each of its angle is 900. So all squares can be called rhombus but converse is not true.
Problem 2: In the figure ROPE is a square. Show that diagonals are equal.
Solution:
In Δ REP and Δ OEP
RE = OP (sides of square)
∠E = ∠P (each 900)
EP = EP (common)
Therefore, triangles are congruent by SAS criteria.
Therefore, RP = OE (c.p.c.t)
Therefore, diagonals of square are equal.
|
41 videos|45 docs|9 tests
|
FAQs on Some Special Parallelograms - Advance Learner Course: Mathematics (Maths) Class 7
| 1. What are some special properties of parallelograms? |  |
| 2. How can I determine if a quadrilateral is a parallelogram? |  |
| 3. What is the relationship between a rectangle and a parallelogram? |  |
| 4. Can a square be considered a parallelogram? |  |
| 5. What are some real-life examples of parallelograms? |  |






















