Step Functions | Calculus - Mathematics PDF Download
Before proceeding into solving differential equations we should take a look at one more function. Without Laplace transforms it would be much more difficult to solve differential equations that involve this function in g(t).
The function is the Heaviside function and is defined as,
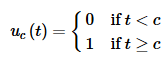
Here is a graph of the Heaviside function.
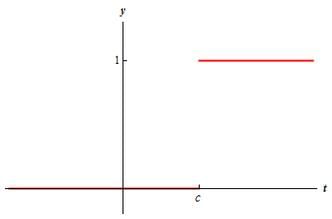
Heaviside functions are often called step functions. Here is some alternate notation for Heaviside functions.
uc(t)=u(t−c)=H(t−c)
We can think of the Heaviside function as a switch that is off until t=c at which point it turns on and takes a value of 1. So, what if we want a switch that will turn on and takes some other value, say 4, or -7?
Heaviside functions can only take values of 0 or 1, but we can use them to get other kinds of switches. For instance, 4uc(t) is a switch that is off until t=c and then turns on and takes a value of 4. Likewise, −7uc(t) will be a switch that will take a value of -7 when it turns on.
Now, suppose that we want a switch that is on (with a value of 1) and then turns off at t=c. We can use Heaviside functions to represent this as well. The following function will exhibit this kind of behavior.
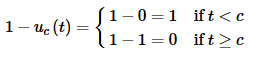
Prior to t=c the Heaviside is off and so has a value of zero. The function as whole then for t<c has a value of 1. When we hit t=c the Heaviside function will turn on and the function will now take a value of 0.
We can also modify this so that it has values other than 1 when it is on. For instance,
3−3uc(t)
will be a switch that has a value of 3 until it turns off at t=c.
We can also use Heaviside functions to represent much more complicated switches.
Example 1 Write the following function (or switch) in terms of Heaviside functions.
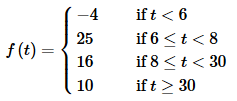
Solution:
There are three sudden shifts in this function and so (hopefully) it’s clear that we’re going to need three Heaviside functions here, one for each shift in the function. Here’s the function in terms of Heaviside functions.
f(t)=−4+29u6(t)−9u8(t)−6u30(t)
It’s fairly easy to verify this.
In the first interval, t<6 all three Heaviside functions are off and the function has the value
f(t)=−4
Notice that when we know that Heaviside functions are on or off we tend to not write them at all as we did in this case.
In the next interval, 6≤t<8 the first Heaviside function is now on while the remaining two are still off. So, in this case the function has the value.
f(t)=−4+29=25
In the third interval, 8≤t<30 the first two Heaviside functions are on while the last remains off. Here the function has the value.
f(t)=−4+29−9=16
In the last interval, t≥30 all three Heaviside function are one and the function has the value.
f(t)=−4+29−9−6=10
So, the function has the correct value in all the intervals.
All of this is fine, but if we continue the idea of using Heaviside function to represent switches, we really need to acknowledge that most switches will not turn on and take constant values. Most switches will turn on and vary continually with the value of t.
So, let’s consider the following function.
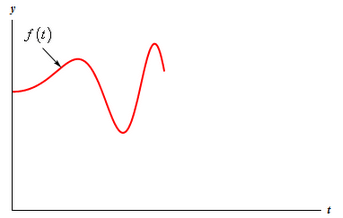
We would like a switch that is off until t=c and then turns on and takes the values above. By this we mean that when t=c we want the switch to turn on and take the value of f(0) and when t = c + 4 we want the switch to turn on and take the value of f(4), etc. In other words, we want the switch to look like the following,
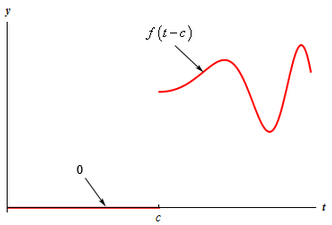
Notice that in order to take the values that we want the switch to take it needs to turn on and take the values of f(t-c)! We can use Heaviside functions to help us represent this switch as well. Using Heaviside functions this switch can be written as
g(t)=uc(t)f(t−c) (1)
Okay, we’ve talked a lot about Heaviside functions to this point, but we haven’t even touched on Laplace transforms yet. So, let’s start thinking about that. Let’s determine the Laplace transform of (1). This is actually easy enough to derive so let’s do that. Plugging (1) into the definition of the Laplace transform gives,
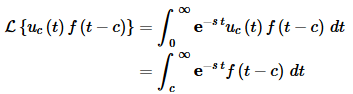
Notice that we took advantage of the fact that the Heaviside function will be zero if t<c and 1 otherwise. This means that we can drop the Heaviside function and start the integral at c instead of 0. Now use the substitution u = t – c and the integral becomes,

The second exponential has no u's in it and so it can be factored out of the integral. Note as well that in the substitution process the lower limit of integration went back to 0.

Now, the integral left is nothing more than the integral that we would need to compute if we were going to find the Laplace transform of f(t). Therefore, we get the following formula
L{uc(t)f(t−c)}=e−csF(s) (2)
In order to use (2) the function f(t) must be shifted by c, the same value that is used in the Heaviside function. Also note that we only take the transform of f(t) and not f(t-c)! We can also turn this around to get a useful formula for inverse Laplace transforms.
L−1{e−csF(s)}=uc(t)f(t−c) (3)
We can use (2) to get the Laplace transform of a Heaviside function by itself. To do this we will consider the function in (2) to be f(t)=1. Doing this gives us
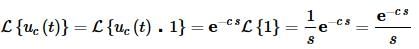
Putting all of this together leads to the following two formulas.
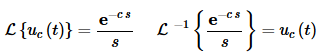 (4)
(4)
Let’s do some examples.
Example 2 Find the Laplace transform of each of the following.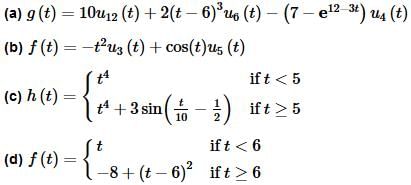
Solution:
In all of these problems remember that the function MUST be in the form
uc(t)f(t−c)
before we start taking transforms. If it isn’t in that form we will have to put it into that form!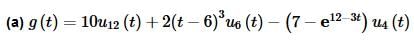
So, there are three terms in this function. The first is simply a Heaviside function and so we can use (4) on this term. The second and third terms however have functions with them and we need to identify the functions that are shifted for each of these. In the second term it appears that we are using the following function,
f(t)=2t3⇒f(t−6)=2(t−6)3
and this has been shifted by the correct amount.
The third term uses the following function,
f(t)=7−e−3t ⇒ f(t−4)=7−e−3(t−4)=7−e12−3t
which has also been shifted by the correct amount.
With these functions identified we can now take the transform of the function.
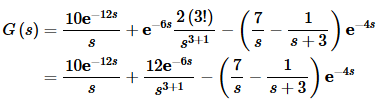
(b) f(t)=−t2u3(t)+cos(t)u5(t)
This part is going to cause some problems. There are two terms and neither has been shifted by the proper amount. The first term needs to be shifted by 3 and the second needs to be shifted by 5. So, since they haven’t been shifted, we will need to force the issue. We will need to add in the shifts, and then take them back out of course. Here they are.
f(t)=−(t−3+3)2u3(t)+cos(t−5+5)u5(t)
Now we still have some potential problems here. The first function is still not really shifted correctly, so we’ll need to use
(a+b)2=a2+2ab+b2
to get this shifted correctly.
The second term can be dealt with in one of two ways. The first would be to use the formula
cos(a+b)=cos(a)cos(b)−sin(a)sin(b)
to break it up into cosines and sines with arguments of t-5 which will be shifted as we expect. There is an easier way to do this one however. From our table of Laplace transforms we have #16 and using that we can see that if
g(t)=cos(t+5) ⇒ g(t−5)=cos(t−5+5)
This will make our life a little easier so we’ll do it this way.
Now, breaking up the first term and leaving the second term alone gives us,
f(t)=−((t−3)2+6(t−3)+9)u3(t)+cos(t−5+5)u5(t)
Okay, so it looks like the two functions that have been shifted here are
g(t)=t2+6t+9
g(t)=cos(t+5)
Taking the transform then gives,
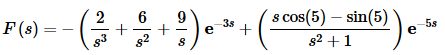
It’s messy, especially the second term, but there it is. Also, do not get excited about the cos(5) and sin(5). They are just numbers.
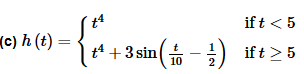
This one isn’t as bad as it might look on the surface. The first thing that we need to do is write it in terms of Heaviside functions.
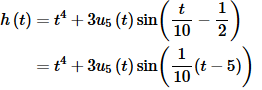
Since the t4 is in both terms there isn’t anything to do when we add in the Heaviside function. The only thing that gets added in is the sine term. Notice as well that the sine has been shifted by the proper amount.
All we need to do now is to take the transform.
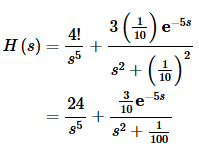
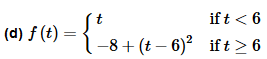
Again, the first thing that we need to do is write the function in terms of Heaviside functions.
f(t)=t+(−8−t+(t−6)2)u6(t)
We had to add in a “-8” in the second term since that appears in the second part and we also had to subtract a t in the second term since the t in the first portion is no longer there. This subtraction of the t adds a problem because the second function is no longer correctly shifted. This is easier to fix than the previous example however.
Here is the corrected function.
f(t)=t+(−8−(t−6+6)+(t−6)2)u6(t)
=t+(−8−(t−6)−6+(t−6)2)u6(t)
=t+(−14−(t−6)+(t−6)2)u6(t)
So, in the second term it looks like we are shifting
g(t)=t2−t−14
The transform is then,
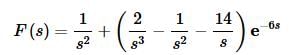
Without the Heaviside function taking Laplace transforms is not a terribly difficult process provided we have our trusty table of transforms. However, with the advent of Heaviside functions, taking transforms can become a fairly messy process on occasion.
So, let’s do some inverse Laplace transforms to see how they are done.
Example 3 Find the inverse Laplace transform of each of the following.
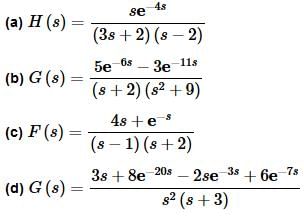
Solution:
All of these will use (3) somewhere in the process. Notice that in order to use this formula the exponential doesn’t really enter into the mix until the very end. The vast majority of the process is finding the inverse transform of the stuff without the exponential.
In these problems we are not going to go into detail on many of the inverse transforms. If you need a refresher on some of the basics of inverse transforms go back and take a look at the previous section.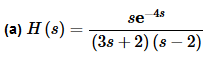
In light of the comments above let’s first rewrite the transform in the following way.
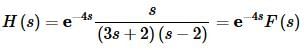
Now, this problem really comes down to needing f(t). So, let’s do that. We’ll need to partial fraction F(s) up. Here’s the partial fraction decomposition.
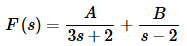
Setting numerators equal gives,
s=A(s−2)+B(3s+2)
We’ll find the constants here by selecting values of s. Doing this gives,
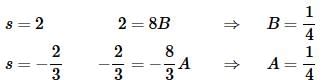
So, the partial fraction decomposition becomes,
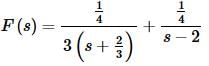
Notice that we factored a 3 out of the denominator in order to actually do the inverse transform. The inverse transform of this is then,

Now, let’s go back and do the actual problem. The original transform was,
H(s)=e−4sF(s)
Note that we didn’t bother to plug in F(s). There really isn’t a reason to plug it back in. Let’s just use (3) to write down the inverse transform in terms of symbols. The inverse transform is,
h(t)=u4(t)f(t−4)
where, f(t) is,
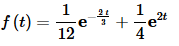
This is all the farther that we’ll go with the answer. There really isn’t any reason to plug in f(t) at this point. It would make the function longer and definitely messier. We will give almost all of our answers to these types of inverse transforms in this form.
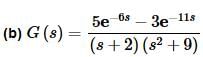
This problem is not as difficult as it might at first appear to be. Because there are two exponentials we will need to deal with them separately eventually. Now, this might lead us to conclude that the best way to deal with this function is to split it up as follows,
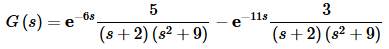
Notice that we factored out the exponential, as we did in the last example, since we would need to do that eventually anyway. This is where a fairly common complication arises. Many people will call the first function F(s) and the second function H(s) and then partial fraction both of them.However, if instead of just factoring out the exponential we would also factor out the coefficient we would get,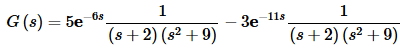
Upon doing this we can see that the two functions are in fact the same function. The only difference is the constant that was in the numerator. So, the way that we’ll do these problems is to first notice that both of the exponentials have only constants as coefficients. Instead of breaking things up then, we will simply factor out the whole numerator and get,
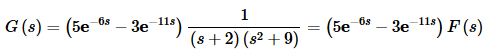
and now we will just partial fraction F(s).
Here is the partial fraction decomposition.
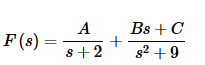
Setting numerators equal and combining gives us,
1=A(s2+9)+(s+2)(Bs+C)
=(A+B)s2+(2B+C)s+9A+2C
Setting coefficient equal and solving gives,
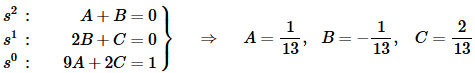
Substituting back into the transform gives and fixing up the numerators as needed gives,
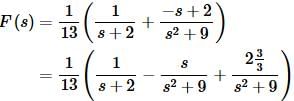
As we did in the previous section we factored out the common denominator to make our work a little simpler. Taking the inverse transform then gives,
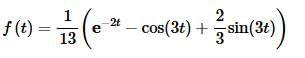
At this point we can go back and start thinking about the original problem.
G(s)=(5e−6s−3e−11s)F(s)
=5e−6sF(s)−3e−11sF(s)
We’ll also need to distribute the F(s) through as well in order to get the correct inverse transform. Recall that in order to use (3) to take the inverse transform you must have a single exponential times a single transform. This means that we must multiply the F(s) through the parenthesis. We can now take the inverse transform,
g(t)=5u6(t)f(t−6)−3u11(t)f(t−11)
where,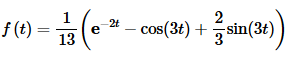
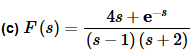
In this case, unlike the previous part, we will need to break up the transform since one term has a constant in it and the other has an s. Note as well that we don’t consider the exponential in this, only its coefficient. Breaking up the transform gives,
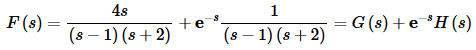
We will need to partial fraction both of these terms up. We’ll start with G(s).
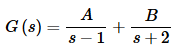
Setting numerators equal gives,
4s=A(s+2)+B(s−1)
Now, pick values of s to find the constants.
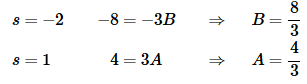
So G(s) and its inverse transform is,
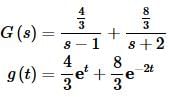
Now, repeat the process for H(s).
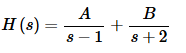
Setting numerators equal gives,
1=A(s+2)+B(s−1)
Now, pick values of s to find the constants.
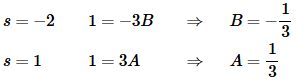
So H(s) and its inverse transform is,
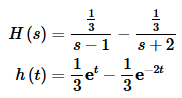
Putting all of this together gives the following,
F(s)=G(s)+e−sH(s)
f(t)=g(t)+u1(t)h(t−1)
where,
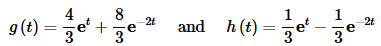
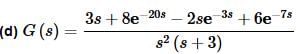
This one looks messier than it actually is. Let’s first rearrange the numerator a little.
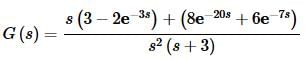
In this form it looks like we can break this up into two pieces that will require partial fractions. When we break these up we should always try and break things up into as few pieces as possible for the partial fractioning. Doing this can save you a great deal of unnecessary work. Breaking up the transform as suggested above gives,
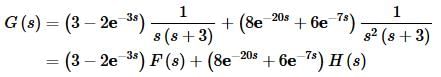
Note that we canceled an s in F(s). You should always simplify as much a possible before doing the partial fractions.
Let’s partial fraction up F(s) first.
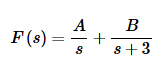
Setting numerators equal gives,
1=A(s+3)+Bs
Now, pick values of s to find the constants.
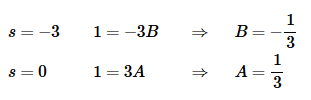
So F(s) and its inverse transform is,
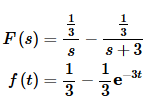
Now partial fraction H(s).
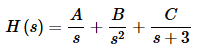
Setting numerators equal gives,
1=As(s+3)+B(s+3)+Cs2
Pick values of s to find the constants.
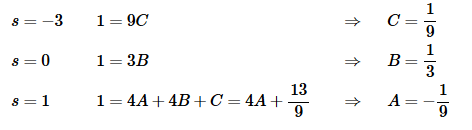
So, H(s) and its inverse transform is,
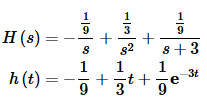
Now, let’s go back to the original problem, remembering to multiply the transform through the parenthesis.
G(s)=3F(s)−2e−3sF(s)+8e−20sH(s)+6e−7sH(s)
Taking the inverse transform gives,
g(t)=3f(t)−2u3(t)f(t−3)+8u20(t)h(t−20)+6u7(t)h(t−7)
So, as this example has shown, these can be a somewhat messy. However, the mess is really only that of notation and amount of work. The actual partial fraction work was identical to the previous sections work. The main difference in this section is we had to do more of it. As far as the inverse transform process goes. Again, the vast majority of that was identical to the previous section as well.
So, don’t let the apparent messiness of these problems get you to decide that you can’t do them. Generally, they aren’t as bad as they seem initially.
|
112 videos|65 docs|3 tests
|
FAQs on Step Functions - Calculus - Mathematics
| 1. What is a step function in mathematics? |  |
| 2. How are step functions useful in real-life applications? |  |
| 3. Can a step function have an infinite number of steps? |  |
| 4. How do you determine the domain and range of a step function? |  |
| 5. Are there any mathematical operations that can be performed on step functions? |  |
















