Solution of Initial value problem (IVP) | Calculus - Mathematics PDF Download
Solving IVP's with Laplace Transforms
It’s now time to get back to differential equations. We’ve spent the last three sections learning how to take Laplace transforms and how to take inverse Laplace transforms. These are going to be invaluable skills for the next couple of sections so don’t forget what we learned there.
Before proceeding into differential equations we will need one more formula. We will need to know how to take the Laplace transform of a derivative. First recall that f(n) denotes the nth derivative of the function f. We now have the following fact.
Fact
Suppose that f, f′, f′′,… f(n−1) are all continuous functions and f(n) is a piecewise continuous function. Then,
Since we are going to be dealing with second order differential equations it will be convenient to have the Laplace transform of the first two derivatives.
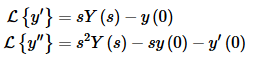
Notice that the two function evaluations that appear in these formulas, y(0) and y′(0), are often what we’ve been using for initial condition in our IVP’s. So, this means that if we are to use these formulas to solve an IVP we will need initial conditions at t=0.
While Laplace transforms are particularly useful for nonhomogeneous differential equations which have Heaviside functions in the forcing function we’ll start off with a couple of fairly simple problems to illustrate how the process works.
Example 1 Solve the following IVP.
y′′−10y′+9y=5t,y(0)=−1y′(0)=2
Solution:
The first step in using Laplace transforms to solve an IVP is to take the transform of every term in the differential equation.
L{y′′}−10L{y′}+9L{y}=L{5t}
Using the appropriate formulas from our table of Laplace transforms gives us the following.
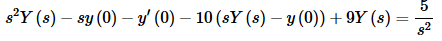
Plug in the initial conditions and collect all the terms that have a Y(s) in them
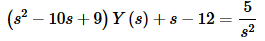
Solve for Y(s).
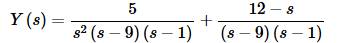
At this point it’s convenient to recall just what we’re trying to do. We are trying to find the solution, y(t), to an IVP. What we’ve managed to find at this point is not the solution, but its Laplace transform. So, in order to find the solution all that we need to do is to take the inverse transform.
Before doing that let’s notice that in its present form we will have to do partial fractions twice. However, if we combine the two terms up we will only be doing partial fractions once. Not only that, but the denominator for the combined term will be identical to the denominator of the first term. This means that we are going to partial fraction up a term with that denominator no matter what so we might as well make the numerator slightly messier and then just partial fraction once.
This is one of those things where we are apparently making the problem messier, but in the process we are going to save ourselves a fair amount of work!
Combining the two terms gives,
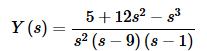
The partial fraction decomposition for this transform is,
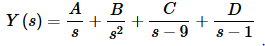
Setting numerators equal gives,
5+12s2−s3=As(s−9)(s−1)+B(s−9)(s−1)+Cs2(s−1)+Ds2(s−9)
Picking appropriate values of s and solving for the constants gives,
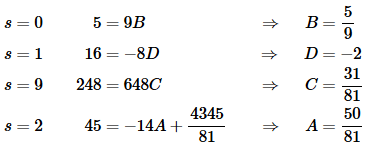
Plugging in the constants gives,
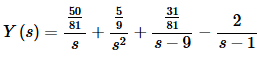
Finally taking the inverse transform gives us the solution to the IVP.
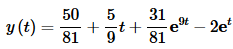
That was a fair amount of work for a problem that probably could have been solved much quicker using the techniques from the previous chapter. The point of this problem however, was to show how we would use Laplace transforms to solve an IVP.
There are a couple of things to note here about using Laplace transforms to solve an IVP. First, using Laplace transforms reduces a differential equation down to an algebra problem. In the case of the last example the algebra was probably more complicated than the straight forward approach from the last chapter. However, in later problems this will be reversed. The algebra, while still very messy, will often be easier than a straight forward approach.
Second, unlike the approach in the last chapter, we did not need to first find a general solution, differentiate this, plug in the initial conditions and then solve for the constants to get the solution. With Laplace transforms, the initial conditions are applied during the first step and at the end we get the actual solution instead of a general solution.
In many of the later problems Laplace transforms will make the problems significantly easier to work than if we had done the straight forward approach of the last chapter. Also, as we will see, there are some differential equations that simply can’t be done using the techniques from the last chapter and so, in those cases, Laplace transforms will be our only solution.
Let’s take a look at another fairly simple problem.
Example 2 Solve the following IVP.
2y′′+3y′−2y=te−2t,y(0)=0y′(0)=−2
Solution:
As with the first example, let’s first take the Laplace transform of all the terms in the differential equation. We’ll the plug in the initial conditions to get,
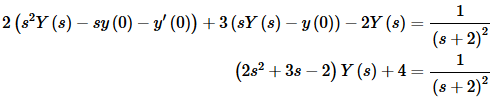
Now solve for Y(s).
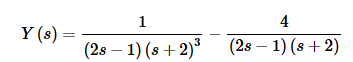
Now, as we did in the last example we’ll go ahead and combine the two terms together as we will have to partial fraction up the first denominator anyway, so we may as well make the numerator a little more complex and just do a single partial fraction. This will give,

The partial fraction decomposition is then,

Setting numerator equal gives,
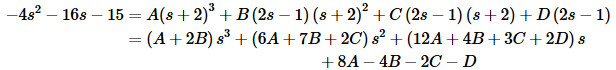
In this case it’s probably easier to just set coefficients equal and solve the resulting system of equation rather than pick values of s. So, here is the system and its solution.
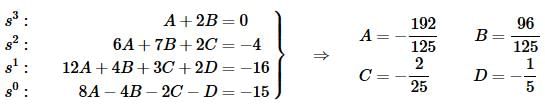
We will get a common denominator of 125 on all these coefficients and factor that out when we go to plug them back into the transform. Doing this gives,
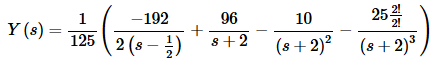
Notice that we also had to factor a 2 out of the denominator of the first term and fix up the numerator of the last term in order to get them to match up to the correct entries in our table of transforms.
Taking the inverse transform then gives,

Example 3 Solve the following IVP.
y′′−6y′+15y=2sin(3t), y(0)=−1 y′(0)=−4
Solution:
Take the Laplace transform of everything and plug in the initial conditions.
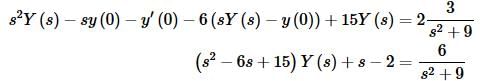
Now solve for Y(s) and combine into a single term as we did in the previous two examples.
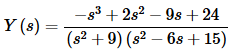
Now, do the partial fractions on this. First let’s get the partial fraction decomposition.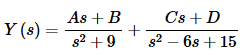
Now, setting numerators equal gives,
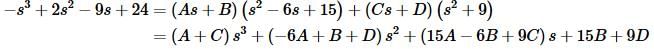
Setting coefficients equal and solving for the constants gives,
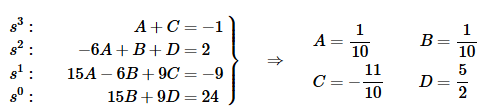
Now, plug these into the decomposition, complete the square on the denominator of the second term and then fix up the numerators for the inverse transform process.
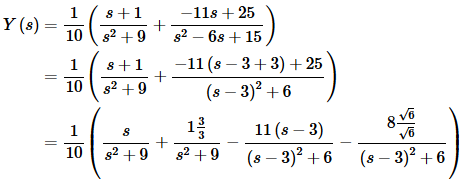
Finally, take the inverse transform.
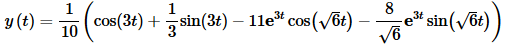
To this point we’ve only looked at IVP’s in which the initial values were at t=0. This is because we need the initial values to be at this point in order to take the Laplace transform of the derivatives. The problem with all of this is that there are IVP’s out there in the world that have initial values at places other than t=0. Laplace transforms would not be as useful as it is if we couldn’t use it on these types of IVP’s. So, we need to take a look at an example in which the initial conditions are not at t=0 in order to see how to handle these kinds of problems.
Example 4 Solve the following IVP.
y′′+4y′=cos(t−3)+4t, y(3)=0 y′(3)=7
Solution:
The first thing that we will need to do here is to take care of the fact that initial conditions are not at t=0. The only way that we can take the Laplace transform of the derivatives is to have the initial conditions at t=0.
This means that we will need to formulate the IVP in such a way that the initial conditions are at t=0. This is actually fairly simple to do, however we will need to do a change of variable to make it work. We are going to define
η=t−3 ⇒ t=η+3
Let’s start with the original differential equation.
y′′(t)+4y′(t) = cos(t−3)+4t
Notice that we put in the (t) part on the derivatives to make sure that we get things correct here. We will next substitute in for t.
y′′(η+3)+4y′(η+3) = cos(η)+4(η+3)
Now, to simplify life a little let’s define,
u(η)=y(η+3)
Then, by the chain rule, we get the following for the first derivative.
By a similar argument we get the following for the second derivative.
u′′(η)=y′′(η+3)
The initial conditions for u(η) are,
u(0)=y(0+3)=y(3)=0
u′(0)=y′(0+3)=y′(3)=7
The IVP under these new variables is then,
u′′+4u′=cos(η)+4η+12, u(0)=0 u′(0)=7
This is an IVP that we can use Laplace transforms on provided we replace all the t’s in our table with η’s. So, taking the Laplace transform of this new differential equation and plugging in the new initial conditions gives,
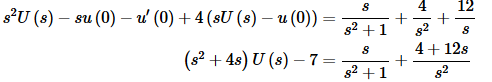
Solving for U(s) gives,
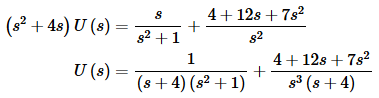
Note that unlike the previous examples we did not completely combine all the terms this time. In all the previous examples we did this because the denominator of one of the terms was the common denominator for all the terms. Therefore, upon combining, all we did was make the numerator a little messier and reduced the number of partial fractions required down from two to one. Note that all the terms in this transform that had only powers of s in the denominator were combined for exactly this reason.
In this transform however, if we combined both of the remaining terms into a single term we would be left with a fairly involved partial fraction problem. Therefore, in this case, it would probably be easier to just do partial fractions twice. We’ve done several partial fractions problems in this section and many partial fraction problems in the previous couple of sections so we’re going to leave the details of the partial fractioning to you to check. Partial fractioning each of the terms in our transform gives us the following.
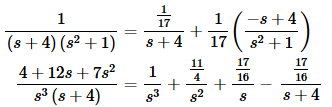
Plugging these into our transform and combining like terms gives us
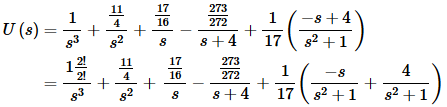
Now, taking the inverse transform will give the solution to our new IVP. Don’t forget to use η’s instead of t’s!
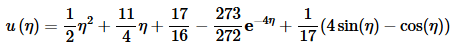
This is not the solution that we are after of course. We are after y(t). However, we can get this by noticing that
y(t)=y(η+3)=u(η)=u(t−3)
So, the solution to the original IVP is,
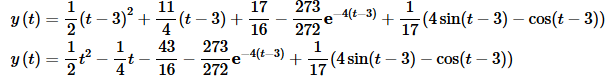
So, we can now do IVP’s that don’t have initial conditions that are at t=0. We also saw in the last example that it isn’t always the best to combine all the terms into a single partial fraction problem as we have been doing prior to this example.
The examples worked in this section would have been just as easy, if not easier, if we had used techniques from the previous chapter. They were worked here using Laplace transforms to illustrate the technique and method.
Nonconstant Coefficient IVP's
In this section we are going to see how Laplace transforms can be used to solve some differential equations that do not have constant coefficients. This is not always an easy thing to do. However, there are some simple cases that can be done.
To do this we will need a quick fact.
Fact
If f(t) is a piecewise continuous function on [0,∞) of exponential order then,
(1)
A function f(t) is said to be of exponential order α if there exists positive constants T and M such that
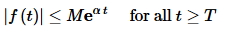
Put in other words, a function that is of exponential order will grow no faster than
Meαt
for some M and α and all sufficiently large t. One way to check whether a function is of exponential order or not is to compute the following limit.
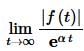
If this limit is finite for some α then the function will be of exponential order α. Likewise, if the limit is infinite for every a then the function is not of exponential order.
Almost all of the functions that you are liable to deal with in a first course in differential equations are of exponential order. A good example of a function that is not of exponential order is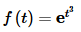
We can check this by computing the above limit.
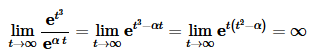
This is true for any value of α and so the function is not of exponential order.
Do not worry too much about this exponential order stuff. This fact is occasionally needed in using Laplace transforms with non constant coefficients.
So, let’s take a look at an example.
Example 1 Solve the following IVP.
y′′+3ty′−6y=2, y(0)=0 y′(0)=0
Solution:
So, for this one we will need to recall that #30 in our table of Laplace transforms tells us that,

So, upon taking the Laplace transforms of everything and plugging in the initial conditions we get,
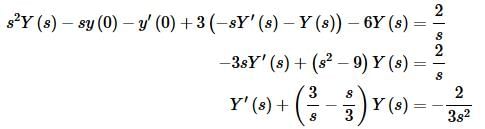
Unlike the examples in the previous section where we ended up with a transform for the solution, here we get a linear first order differential equation that must be solved in order to get a transform for the solution.
The integrating factor for this differential equation is,
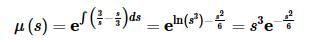
Multiplying through, integrating and solving for Y(s) gives,
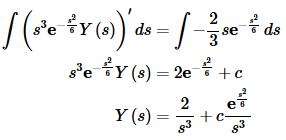
Now, we have a transform for the solution. However, that second term looks unlike anything we’ve seen to this point. This is where the fact about the transforms of exponential order functions comes into play. We are going to assume that whatever our solution is, it is of exponential order. This means that
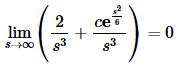
The first term does go to zero in the limit. The second term however, will only go to zero if c=0. Therefore, we must have c=0 in order for this to be the transform of our solution.
So, the transform of our solution, as well as the solution is,
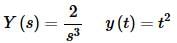
We’ll leave it to you to verify that this is in fact a solution if you’d like to.
Now, not all nonconstant differential equations need to use (1). So, let’s take a look at one more example.
Example 2 Solve the following IVP.
ty′′−ty′+y=2, y(0)=2 y′(0)=−4
Solution:
From the first example we have,
L{ty′}=−sY′(s)−Y(s)
We’ll also need,
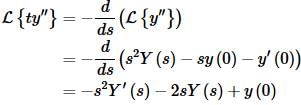
Taking the Laplace transform of everything and plugging in the initial conditions gives,
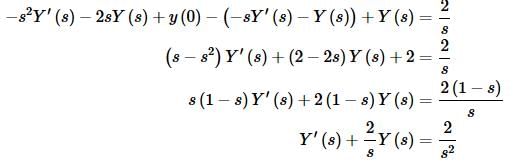
Once again we have a linear first order differential equation that we must solve in order to get a transform for the solution. Notice as well that we never used the second initial condition in this work. That is okay, we will use it eventually.
Since this linear differential equation is much easier to solve compared to the first one, we’ll leave the details to you. Upon solving the differential equation we get,
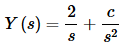
Now, this transform goes to zero for all values of c and we can take the inverse transform of the second term. Therefore, we won’t need to use (1) to get rid of the second term as did in the previous example.
Taking the inverse transform gives,
y(t)=2+ct
Now, this is where we will use the second initial condition. Upon differentiating and plugging in the second initial condition we can see that c=−4.
So, the solution to this IVP is,
y(t)=2−4t
So, we’ve seen how to use Laplace transforms to solve some nonconstant coefficient differential equations. Notice however that all we did was add in an occasional t to the coefficients. We couldn’t get too complicated with the coefficients. If we had we would not have been able to easily use Laplace transforms to solve them.
Sometimes Laplace transforms can be used to solve nonconstant differential equations, however, in general, nonconstant differential equations are still very difficult to solve.
IVP's With Step Functions
In this section we will use Laplace transforms to solve IVP’s which contain Heaviside functions in the forcing function. This is where Laplace transform really starts to come into its own as a solution method.
To work these problems we’ll just need to remember the following two formulas,
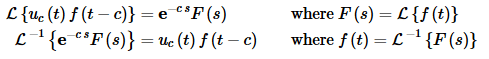
In other words, we will always need to remember that in order to take the transform of a function that involves a Heaviside we’ve got to make sure the function has been properly shifted.
Let’s work an example.
Example 1 Solve the following IVP.
y′′−y′+5y=4+u2(t)e4−2t, y(0)=2 y′(0)=−1
Solution:
First let’s rewrite the forcing function to make sure that it’s being shifted correctly and to identify the function that is actually being shifted.
y′′−y′+5y=4+u2(t)e−2(t−2)
So, it is being shifted correctly and the function that is being shifted is e−2t. Taking the Laplace transform of everything and plugging in the initial conditions gives,
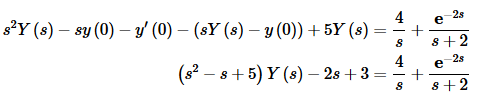
Now solve for Y(s).
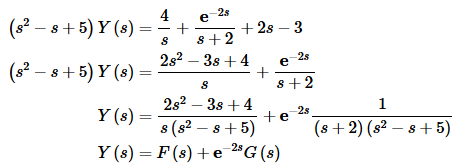
Notice that we combined a couple of terms to simplify things a little. Now we need to partial fraction F(s) and G(s). We’ll leave it to you to check the details of the partial fractions.
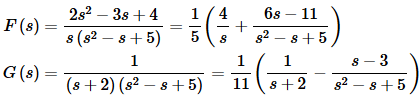
We now need to do the inverse transforms on each of these. We’ll start with F(s).
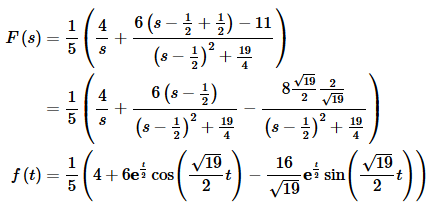
Now G(s).
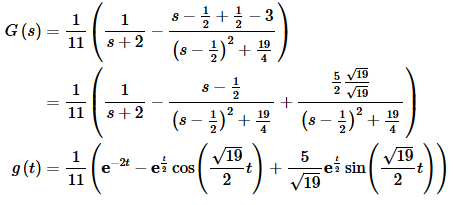
Okay, we can now get the solution to the differential equation. Starting with the transform we get,
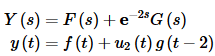
where f(t) and g(t) are the functions shown above.
There can be a fair amount of work involved in solving differential equations that involve Heaviside functions.
Let’s take a look at another example or two.
Example 2 Solve the following IVP.
y′′−y′=cos(2t)+cos(2t−12)u6(t) y(0)=−4, y′(0)=0
Solution:
Let’s rewrite the differential equation so we can identify the function that is actually being shifted.
y′′−y′=cos(2t)+cos(2(t−6))u6(t)
So, the function that is being shifted is cos(2t) and it is being shifted correctly. Taking the Laplace transform of everything and plugging in the initial conditions gives,
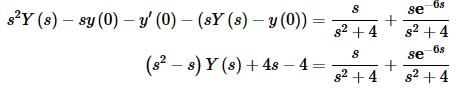
Now solve for Y(s).
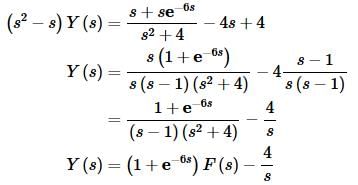
Notice that we combined the first two terms to simplify things a little. Also, there was some canceling going on in this one. Do not expect that to happen on a regular basis. We now need to partial fraction F(s). We’ll leave the details to you to check.
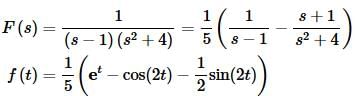
Okay, we can now get the solution to the differential equation. Starting with the transform we get,
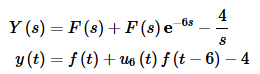
where f(t) is given above.
Example 3 Solve the following IVP.
y′′−5y′−14y=9+u3(t)+4(t−1)u1(t) y(0)=0, y′(0)=10
Solution :
Let’s take the Laplace transform of everything and note that in the third term we are shifting 4t.
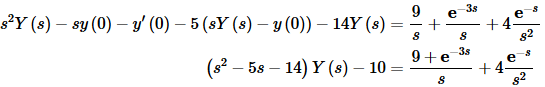
Now solve for Y(s).
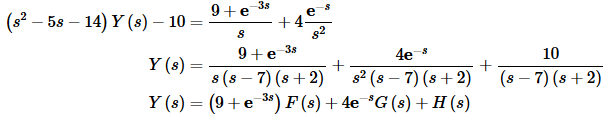
So, we have three functions that we’ll need to partial fraction for this problem. I’ll leave it to you to check the details.
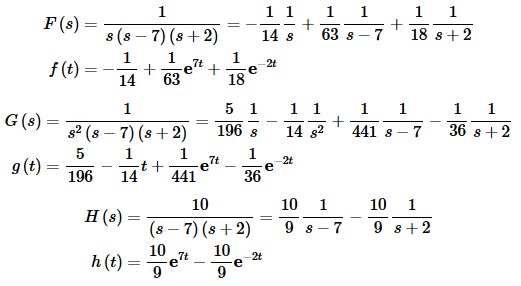
Okay, we can now get the solution to the differential equation. Starting with the transform we get,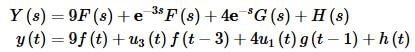
where f(t), g(t) and h(t) are given above.
Let’s work one more example.
Example 4 Solve the following IVP.
y′′+3y′+2y=g(t), y(0)=0 y′(0)=−2
where,
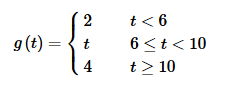
Solution:
The first step is to get g(t) written in terms of Heaviside functions so that we can take the transform.
g(t)=2+(t−2)u6(t)+(4−t)u10(t)
Now, while this is g(t) written in terms of Heaviside functions it is not yet in proper form for us to take the transform. Remember that each function must be shifted by a proper amount. So, getting things set up for the proper shifts gives us,
g(t)=2+(t−6+6−2)u6(t)+(4−(t−10+10))u10(t)
g(t)=2+(t−6+4)u6(t)+(−6−(t−10))u10(t)
So, for the first Heaviside it looks like f(t)=t+4 is the function that is being shifted and for the second Heaviside it looks like f(t)=−6−t is being shifted.
Now take the Laplace transform of everything and plug in the initial conditions.
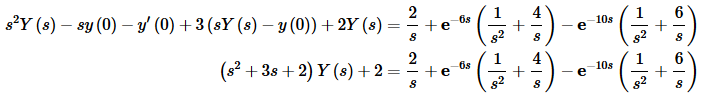
Solve for Y(s).
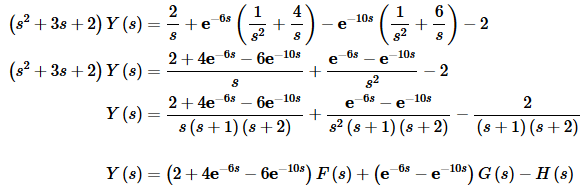
Now, in the solving process we simplified things into as few terms as possible. Even doing this, it looks like we’ll still need to do three partial fractions.
We’ll leave the details of the partial fractioning to you to verify. The partial fraction form and inverse transform of each of these are.

Putting this all back together is going to be a little messy. First rewrite the transform a little to make the inverse transform process possible.
Y(s)=2F(s)+e−6s(4F(s)+G(s))−e−10s(6F(s)+G(s))−H(s)
Now, taking the inverse transform of all the pieces gives us the final solution to the IVP.
y(t)=2f(t)−h(t)+u6(t)(4f(t−6)+g(t−6))−u10(t)(6f(t−10)+g(t−10))
where f(t), g(t), and h(t) are defined above.
So, the answer to this example is a little messy to write down, but overall the work here wasn’t too terribly bad.
Before proceeding with the next section let’s see how we would have had to solve this IVP if we hadn’t had Laplace transforms. To solve this IVP we would have had to solve three separate IVP’s. One for each portion of g(t). Here is a list of the IVP’s that we would have had to solve.
- 0<t<6
y′′+3y′+2y=2, y(0)=0 y′(0)=−2
The solution to this IVP, with some work, can be made to look like,
y1(t)=2f(t)−h(t) - 6≤t<10
y′′+3y′+2y=t, y(6)=y1(6) y′(6)=y′1(6)
where, y1(t) is the solution to the first IVP. The solution to this IVP, with some work, can be made to look like,
y2(t)=2f(t)−h(t)+4f(t−6)+g(t−6) - t≥10
y′′+3y′+2y=4, y(10)=y2(10) y′(10)=y′2(10)
where, y2(t) is the solution to the second IVP. The solution to this IVP, with some work, can be made to look like,
y3(t)=2f(t)−h(t)+4f(t−6)+g(t−6)−6f(t−10)−g(t−10)
There is a considerable amount of work required to solve all three of these and in each of these the forcing function is not that complicated. Using Laplace transforms saved us a fair amount of work.
|
112 videos|65 docs|3 tests
|
FAQs on Solution of Initial value problem (IVP) - Calculus - Mathematics
| 1. What is an initial value problem (IVP) in mathematics? |  |
| 2. How do you solve an initial value problem (IVP) in mathematics? |  |
| 3. What are the applications of initial value problems in mathematics? |  |
| 4. Can all differential equations be solved as initial value problems? |  |
| 5. Are there numerical methods available to solve initial value problems? |  |
















