JEE Advanced (Subjective Type Questions): Rotational Motion | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. A 40 kg mass, hanging at the end of a rope of length l, oscillates in a vertical plane with an angular amplitude θ0.What is the tension in the rope when it makes an engle θ with the vertical? If the breaking strength of the rope is 80 kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?
Ans.
Solution. 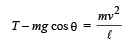
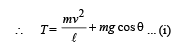
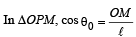
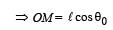
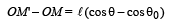
Loss in potential energy = Gain in kinetic energy (ActivityP to P')
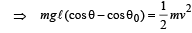
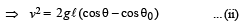
From (i) and (ii)
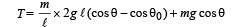
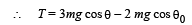
From equation (i) it is clear that the tension is maximum when cos θ = 1 i.e., θ = 0°
∴ T = mg
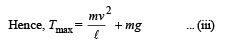
From eqn. (ii)
v2 = 2 g l(1 - cosθ0) ... (iv)
From (iii) and (iv)
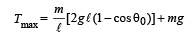
80 = 3 × 40 – 2 × 40 cosθ0
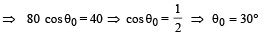
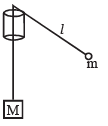
Q.2. A large mass M and a small mass m hang at two ends of a string that passes over a smooth tube as shown in the figure. The mass m moves around a circular path which lies in a horizontal plane. The length of string from the mass m to the top of the tube is l and θ is the ‘angle’ this length makes with the vertical. What should be the frequency of rotation of mass m, so that the mass M remains stationary?
Ans.
Solution.
Suppose mass m moves around a circular path of radius r.
Let the string makes an angle q with the vertical. Resolving tension T, we get and,
T sin θ = mrω2 ... (i)
T cos θ = mg ... (ii)
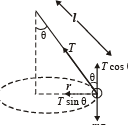
From diagram, sin θ =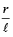
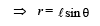
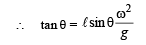
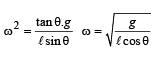
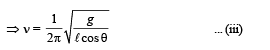
From (ii), T cosθ = mg.
For M to remain stationary, T = Mg
∴ Mg cos θ = mg
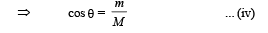
From (iii) and (iv), n =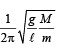
Q.3. A circular plate of uniform thickness has a diameter of 56 cm.
A circular portion of diameter 42 cm is removed from one edge of the plate as shown in figure. Find the position of the centre of mass of the remaining portion.
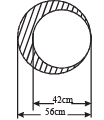
Ans. 9 cm from the origin towards left
Solution.
Let s be the mass per unit area.
Then the mass of the whole disc = σ × πR2
Mass of the portion removed = σ ×πr2
R = 28 cm; r = 21 cm; OP = 7 cm
Taking O as the origin
The position of c.m.
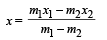
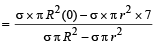
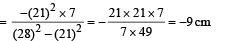
This means that the c.m. lies at a distance of 9 cm from the origin towards left.
Q.4. A block of mass M with a semicircular of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the top point A (see Fig).
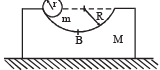
The cylinder slips on the semicircular frictionless track.
How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track ?
Ans.
Solution. C.M. of the system of two bodies in situation (i) in x-coordinate
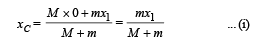
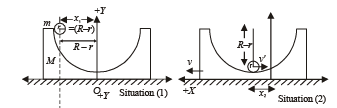
C.M. of the system in situation (ii) in x-coordinate is
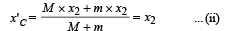
Since no external force is in x-direction
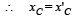
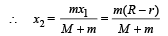
Applying conservation of linear momentum, Initial Momentum = Final Momentum
0 = MV – mv

Applying the concept of conservation of energy, we get Loss in P.E. of mass m = Gain in K.E. of m
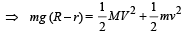
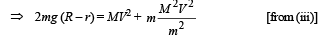
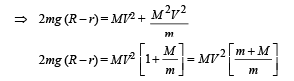
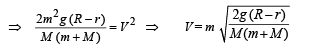
Q.5. A particle is projected at time t= 0 from a point P on the ground with a speed v0, at an angle of 45° to the horizontal.
Find the magnitude and direction of the angular momentum of the particle about P at time t = v0/g
Ans. perpendicular to the plane of motion and is directed away from the reader..
Solution. The angular momentum is given by L = xpy – ypx = m[xvy – yvx]
(x, y) are the coordinates of the particle after time t = v0 /g and
vx, vy are the components of velocities at that time.
For vx and vy
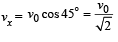
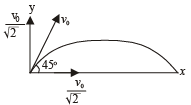
(The horizontal velocity does not change with time) Applying v = u + at in the vertical direction to find vy
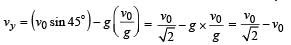
For x and y In horizontal direction x = vx*t
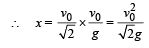
In vertical direction applying
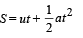
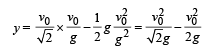
Putting the values in the above equation
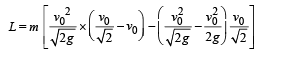
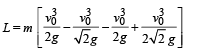
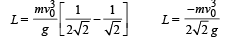
Note : The direction of L is perpendicular to the plane of motion and is directed away from the reader.
Q.6. A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part, The horizontal part is 1.0 metre above the ground level and the top of the track is 2.4 metres above the ground. Find the distance on the ground with respect to the point B (which is vertically below the end of the track as shown in fig.) where the sphere lands. During its flight as a projectile, does the sphere continue to rotate about its centre of mass? Explain.

Ans. 2m, yes
Solution. KEY CONCEPT : Applying law of conservation of energy at point D and point A P.E. at D = P.E. at Q + (K.E.)T + (K.E.)R where (K.E.)T = Translational K.E. and (K.E.)R = Rotational K.E.
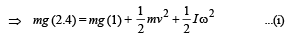
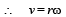
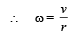
where r is the radius of the sphere

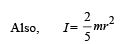
Putting in equation (i)
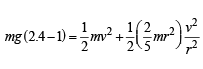
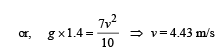
After point Q, the body takes a parabolic path.
The vertical motion parameters of parabolic motion will be

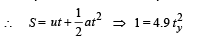
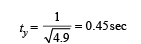
Applying this time in horizontal motion of parabolic path, BC = 4.43 × 0.45 = 2m
Note : During its flight as a projectile, the sphere continues
Q.7. A thin uniform bar lies on a frictionless horizontal surface and is free to move in any way on the surface. Its mass is 0.16 kg and length √3 meters. Two particles, each of mass 0.08 kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10 m/s, and other with 6 m/s as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distance of 0.5m from the centre of the bar. The particles strike the bar at the same instant of time and stick to the bar on collision. Calculate the loss of the kinetic energy of the system in the above collision process.
Ans. 2.72 J
Solution. Initial Kinetic Energy
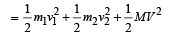
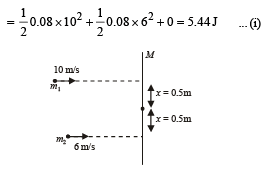
Applying law of conservation of linear momentum during collision
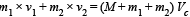
where Vc is the velocity of centre of mass of the bar and particles sticked on it after collision 0.08 × 10 + 0.08 × 6 = (0.16 + 0.08 + 0.08) Vc
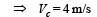
∴ Translational kinetic energy after collision
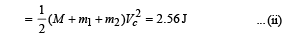 Applying conservation of angular momentum of the bar and two particle system about the centre of the bar.
Applying conservation of angular momentum of the bar and two particle system about the centre of the bar.
Since external torque is zero, the initial angular momentum is equal to final angular momentum.
Initial angular momentum
= m1v1 × x – m2v2x
= 0.08 × 10 × 0.5 – 0.08 × 6 × 0.5
= 0.4 – 0.24 = 0.16 kg m2s–1
(In clockwise direction) Final angular momentum = Iω
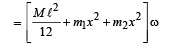
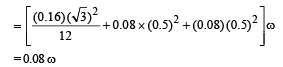
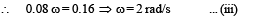
The rotational kinetic energy
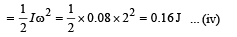
The final kinetic energy
= Translational K.E. + Rotational K.E.
= 2.56 + 0.16 = 2.72 J
The change in K.E. = Initial K.E. – Final K.E.
= 5.44 – 2.72 = 2.72 J
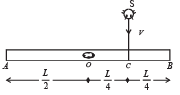
Q.8. A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the centre O in such a way that it can rotate freely in the vertical plane (Fig). The rod is initially in the horizontal position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity ω .
(a) Determine the angular velocity ω in terms of V and L. (b) If the insect reaches the end B when the rod has turned through an angle of 90°, determine V.
 Ans.
Ans.
Solution.
(a) Let us consider the system of homogeneous rod and insect and apply conservation of angular momentum during collision about the point O.
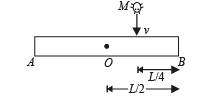
Angular momentum of the system before collision = angular momentum of the system after collision.
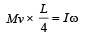
Where I is the moment of inertia of the system just after collision and w is the angular velocity just after collision.
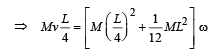
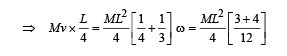
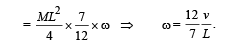
(b) Note : Initially the torque due to mass OB of the rod (acting in clockwise direction) was balanced by the torque due to mass OA of the rod (acting in anticlockwise direction).
But after collision there is an extra mass M of the insect which creates a torque in the clockwise direction, which tends to create angular acceleration in the rod. But the same is compensated by the movement of insect towards B due to which moment of inertia I of the system increases.
Let at any instant of time t the insect be at a distance x from the centre of the rod and the rod has turned through an angle q (= ωt) w.r.t its original position.
Instantaneous torque,
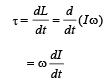
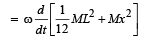
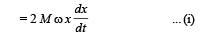
This torque is balanced by the torque due to weight of insect.
τ= Force × Perpendicular distance of force with axis of
rotation = Mg × (OM)
= Mg (x cosθ) ... (ii)
From (i) and (ii)
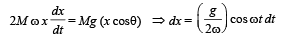
On integration, taking limits

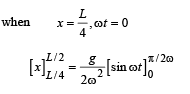
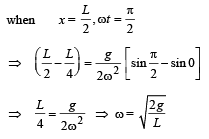
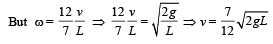
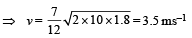
Q.9. A uniform thin rod of mass M and length L is standing vertically along the y-axis on a smooth horizontal surface, with its lower end at the origin (0, 0). A slight disturbance at t = 0 causes the lower end to slip on the smooth surface along the positive x-axis, and the rod starts falling.
(i) What is the path followed by the centre of mass of the rod during its fall? (ii) Find the equation to the trajectory of a point on the rod located at a distance r from the lower end. What is the shape of the path of this point?
Ans.
Solution. (i) Initially, the rod stands vertical. A straight disturbance makes the rod to rotate. While rotating, the force acting on the rod are its weight and normal reaction. These forces are vertical forces and cannot create a horizontal motion.
Therefore the centre of mass of the rod does not move horizontally. The center of mass moves vertically downwards. Thus the path of the center of mass is a straight line.
(ii) Trajectory of an arbitrary point of the rod Consider an arbitrary point P on the rod located at (x, y) and at a distance r from the end B. Let q be the angle of inclination of the rod with the horizontal at this position.
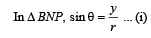
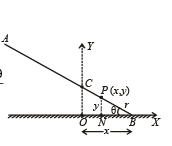
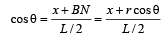
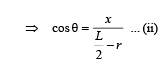
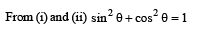
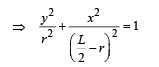
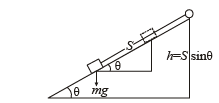
This is equation of an ellipse.
Q.10. A block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination 30° to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2 kg and of radius 0.2 m as shown in Figure.
The drum is given an initial angular velocity such that the block X starts moving up the plane.
(i) Find the tension in the string during the motion.
(ii) At a certain instant of time the magnitude of the angular velocity of Y is 10 rad s–1 calculate the distance travelled by X from that instant of time until it comes to rest
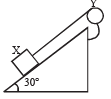
Ans. (i) 1.63N (ii) 1.22 m
Solution. (i) The drum is given an initial velocity such that the block X starts moving up the plane.

As the time passes, the velocity of the block decreases. The linear retardation a, of the block X is given by
mg sin θ - T= ma ... (i)
The linear retardation of the block and the angular acceleration of the drum (∝) are related as
a = R∝ ... (ii)
where R is the radius of the drum.
The retarding torque of the drum is due to tension T in the string.
τ = T × R
But τ = I∝. where I = M.I. of drum about its axis of rotation.
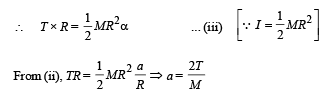
Substituting this value in (i)
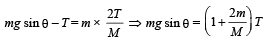
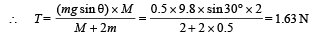
(ii) The total kinetic energy of the drum and the block at the instant when the drum is having angular velocity 10 rads–1 gets converted into the potential energy of the block.
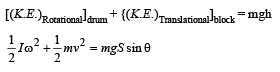
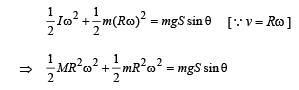
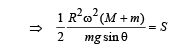
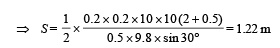 Q.11. Two uniform thin rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02 kg respectively are rigidly joined end to end. The combination is pivoted at the lighter end, P as shown in fig. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05 kg, moving horizontally, hits the lower end of the combination and sticks to it.
Q.11. Two uniform thin rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02 kg respectively are rigidly joined end to end. The combination is pivoted at the lighter end, P as shown in fig. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05 kg, moving horizontally, hits the lower end of the combination and sticks to it.
What should be the velocity of the object so that the system could just be raised to the horizontal position.
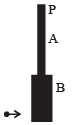
Ans. 6.3 m/s
Solution. During collision, the torque of the system about P will be zero because the only force acting on the system is through P (namely weight of rods/mass m/reaction at P)
Given : l = 0.6 m
mA = 0.01 kg
mB = 0.02 kg
m = 0.05 kg
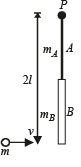
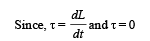
⇒ L is constant.
Angular momentum before collision = mv × 2 l ... (i)
Angular momentum after collision = Iω ... (ii)
Where I is the moment of inertia of the system after collision about P and w is the angular velocity of the system.
M.I. about P : I1 = M.I. of mass m
I2 = M.I. of rod mA
I3 = M.I. of rod mB
I = I1 + I2 + I3
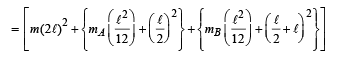
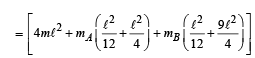
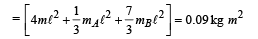
From (i) and (ii)
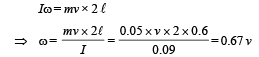
Applying conservation of mechanical energy after collision. (Using the concept of mass) Loss of K.E. = Gain in P.E.
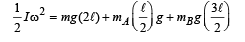
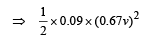
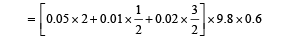
⇒ v = 6.3 m/s
Q.12. A rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radius R is placed horizontally at rest its length parallel to the edge such that the axis of the cylinder and the edge of the block are in the same vertical plane as shown in the figure below. There is sufficient friction present at the edge so that a very small displacement causes the cylinder to roll off the edge without slipping. Determine:
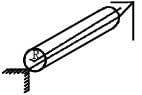
(a) the angle θc through which the cylinder rotates before it leaves contact with the edge, (b) the speed of the centre of mass of the cylinder before leaving contact with the edge, and (c) the ratio of the translational to rotational kinetic energies of the cylinder when its centre of mass is in horizontal line with the edge.
Ans.
Solution. (a) Let the original position of centre of mass of the cylinder be O. While rolling down off the edge, let the cylinder be at such a position that its centre of mass is at a position O'. Let∠NPO be θ. As the cylinder is rolling, the c.m. rotates in a circular path. The centripetal force required for the circular motion is given by the equation.
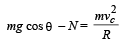
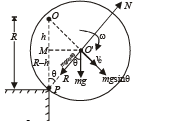
Where N is the normal reaction and m is mass of cylinder.
The condition for the cylinder leaving the edge is N = 0
Applying energy conservation from O to O'.
Loss of potential energy of cylinder
= Gain in translational K.E. + Gain in rotational K.E.
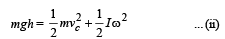
Where I is the moment of inertia of the cylinder about O', its axis of rotation, w is the angular speed, Vc is the velocity of center of mass.
Also for rolling, vc = wR

From (ii), (iii) and (iv), we get
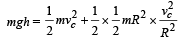
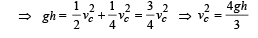

From (i) and (v), we get
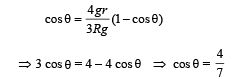
(b) From (v) speed of C.M. of cylinder before leaving contact with edge.
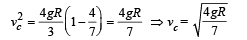
(c) Before the cylinder's c.m. reaches the horizontal line of the edge, it leaves contact with the edge as
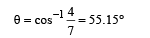
Therefore the rotational K.E., which the cylinder gains at the time of leaving contact with the edge remains the same in its further motion. Thereafter the cylinder gains translational K.E.
Again applying energy conservation from O to the point where c.m. is in horizontal line with edge
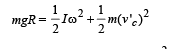
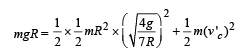
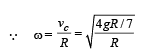
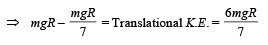
Also, Rotational K.E.


Q.13.
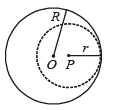
A small sphere of radius R is held against the inner surface of a larger sphere of radius 6R (Fig. P-3).
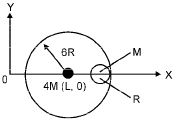
The masses of large and small spheres are 4M and M, respectively, This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position
Ans. (L + 2R, 0)
Solution. KEY CONCEPT : The concept of center of mass can be applied in this problem.
When small sphere M changes its position to other extreme position, there is no external force in the horizontal direction.
Therefore the x-coordinate of c.m. will not change.

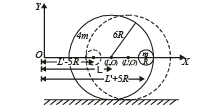
Thin line of sphere represents initial state, dotted line of sphere represents final state.
From (i)
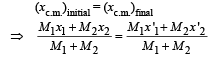
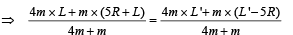
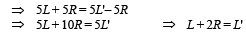
Since, the individual center of mass of the two spheres has a y co-ordinate zero in its initial state and its final state therefore the y-coordinate of c.m. of the two sphere system will remain zero.
Therefore the coordinate of c.m. of bigger sphere is (L + 2R, 0).
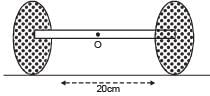
Q.14.Two thin circular disks of mass 2 kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. The axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z axis as the vertically upwards direction. If the truck has an acceleration of 9 m/s2.
Calculate:
(i) The force of friction on each disk, (ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms
Ans.
Solution. (i) The observer, let us suppose, is on the accelerated frame. Therefore a pseudo force ma is applied individually on each disc on the centre of mass. The frictional force is acting in the + X direction which is producing an angular acceleration ∝.
The torque acting on the
disc is
τ = I∝ = f × R
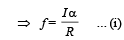

Let a' is the acceleration of c.m. of the disc as seen by the observer. Since the case is of pure rolling and from the perspective of the observer
a' =∝R ... (ii)
⇒ From (i) and (ii)

Applying Newton's law for motion in X-direction ma – f = ma'
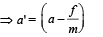
Also moment of inertia

From (iii), (iv) and (v)
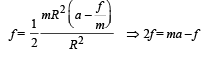
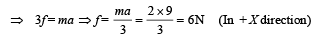
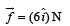
(ii) The position vector of point M, taking O as the origin
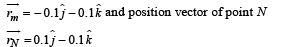
The torque due to friction on disc 1 about O
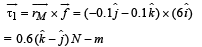
The torque due to friction on disc 2 about O
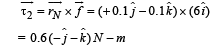
The magnitude of torque on each disc
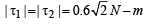
Q.15. A wedge of mass m and triangular cross-section (AB = BC = CA = 2R) is moving with a constant velocity -viˆ towards a sphere of radius R fixed on a smooth horizontal table as shown in Figure. The wedge makes an elastic collision with the fixed sphere and returns along the same path without any rotation. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very short time. Δt, during which the sphere exerts a constant force F on the wedge.
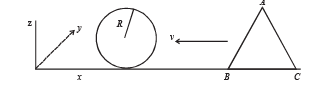
(a) Find the force F and also the normal force N exerted by the table on the wedge during the time Δt.
(b) Let h denote the perpen dicular distance between the centre of mass of the wedge and the line of action of F. Find the magnitude of the torque due to the normal force N about the centre of the wedge, during the interval Δt.
Ans.
Solution. 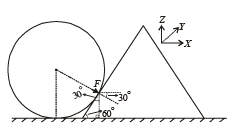
Resolving the force F acting on the wedge
Fx = F cos 30°; Fy = F sin 30°
Note : The collision is elastic and since the sphere is fixed, the wedge will return back with the same velocity (in magnitude).
The force responsible to change the velocity of the wedge in X-direction is Fx.
Fx ×Δt = mv – ( – mv) (Impulse) = (Change in momentum)
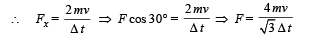
In vector terms
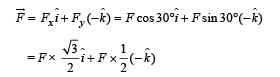
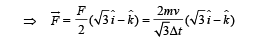
Taking equilibrium of force in Z-direction (acting on wedge) we get
Fy + mg = N

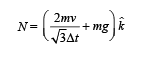
(b) Taking torques on wedge about the c.m. of the wedge.
F × h – Torque due to N + mg × 0 = 0

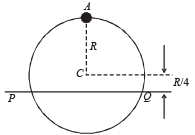
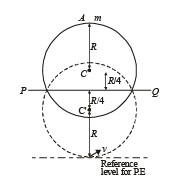
Q.16. A uniform circular disc has radius R and mass m. A particle also of mass m, is fixed at a point A on the edge of the disc as shown in Figure. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance R/4 from the centre C of the disc.The line AC is perpendicular to PQ.
Initially, the disc is held vertical with the point A at its highest position. It is then allowed to fall so that it starts rotating about PQ. Find the linear speed of the particle as it reaches its lowest position.
Ans.
Solution. KEY CONCEPT : During the fall, the disc-mass system gains rotational kinetic energy. This is at the expense of potential energy.
Applying energy conservation Total energy initially = total energy finally
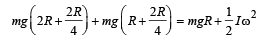
Where I = M.I. of disc-mass system about PQ
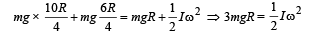
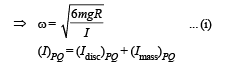
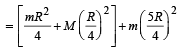
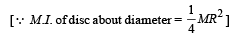
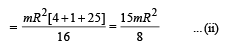
From (i) and (ii)
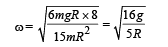
Let v be the velocity of mass m at the lowest point of rotation
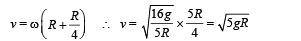
Q.17. A man pushes a cylinder of mass m1 with the help of a plank of mass m2 as shown in Figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
Find
(a) the accelerations of the plank and the center of mass of the cylinder, and (b) the magnitudes and directions of frictional forces at contact points.
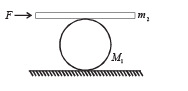
Ans. Solution.
The man applies a force F in the horizontal direction on the plank as shown. Therefore the point of contact of the plank with the cylinder will try to move towards right. Therefore the friction force F will act towards left on the plank. To each and every action there is equal and opposite reaction. Therefore a frictional force f will act on the top of the cylinder towards right.
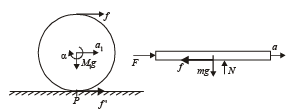
Direction of f ' : A force f is acting on the cylinder. This force is trying to move the point of contact P towards right by an acceleration

At the same time, the force f is trying to rotate the cylinder about its centre of mass.
f × R = I × α
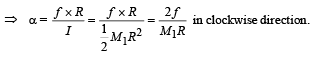
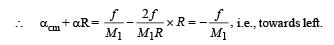
Therefore, the point of contact of the cylinder with the ground move towards left. Hence friction force acts towards right on the cylinder.
Note : You can assume any direction of friction at the point of contact and solve the problem. If the value of friction comes out to be positive, our assumed direction is correct otherwise the direction of friction is opposite. The above activity is done so that if only the direction of friction is asked, an approach may be developed.
Applying Newton's law on plank, we get

Because a2 is the acceleration of topmost point of cylinder and there is no slipping.
Applying Newton's law on cylinder
M1a1 = f + f ' ... (iii)
The torque equation for the cylinder is
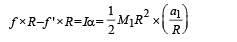
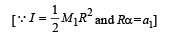
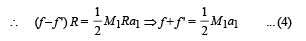
Solving equation (iii) and (iv), we get


From (i) and (iii)
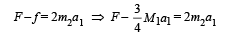
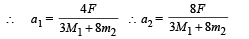
From (v) and (vi)
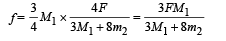
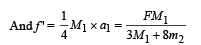
Q.18. Two h eavy met all ic plates are joined together at 90o to each other. A laminar sheet of mass 30 kg is hinged at the line AB joining the two heavy metallic plates. The hinges are frictionless. The moment of inertia of the laminar sheet about an axis parallel to AB and passing through its center of mass is 1.2 kgm2. Two rubber obstacles P and Q are fixed, one on each metallic plate at a distance 0.5 m from the line AB. This distance is chosen so that the reaction due to the hinges on the laminar sheet is zero during the impact.
Initially the laminar sheet hits one of the obstacles with an angular velocity 1 rad/s and turns back. If the impulse on the sheet due to each obstacle is 6 N-s, (a) Find the location of the center of mass of the laminar sheet from AB. (b) At what angular velocity does the laminar sheet come back after the first impact? (c) After how many impacts, does the laminar sheet come to rest?
Ans. (a) 0.1 m (b) 1 radian/sec. (c) infinite
Solution. Ic = 1.2 kg -m2
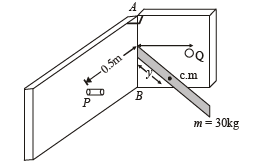
Let y be the distance of c.m. from line AB.
Applying parallel axis theorem of M.I. we get
M.I. of laminar sheet about AB
IAB = Ic.m. + my2
IAB = 12 + 30y2 ... (i)
The angular velocity of the laminar sheet will change after every impact because of impulse.
Impulse = Change in linear momentum
6 = 30 (Vf – Vi)
6 = 30 × y (ωf – ωi) ... (ii)
Also, change in angular momentum = Moment of Impulse
∴ IABωf – IABωi = Impulse × distance
IAB (wf – wi) = 6 ×0.5 = 3

Note : Minus sign with wi because the direction of laminar plate towards the obstacle is taken as – ve (assumption).
From (ii) and (iii)
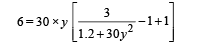
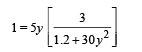
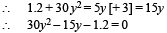
On solving, we get y = 0.1 or 0.4
(Not valid as per sign convention) Now, since the lamina sheet comes back with same angular speed as that of incident angular speed, the sheet will swing in between P and Q infinitely.
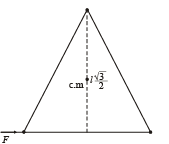
Q.19. Three particles A, B and C, each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l . This body is placed on a horizontal frictioness table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A (see figure). The body is set into rotational motion on the table about A with a constant angular velocity ω.
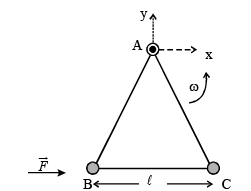
(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
Ans. √3mlω2 (b) (f net)x =-f/4 , (F net)y=√3mlω2
Solution. (a) The mass B is moving
in a circular path centred atA. The centripetal force (m l ω2) required for this circular motion is provided by F '. Therefore a force F ' acts on A (the hinge) which is equal to m l ω2. The same is the case for mass C. Therefore the net force on the hinge is
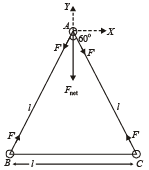
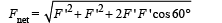
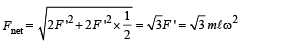
(b) The force F acting on B will provide a torque to the system. This torque is
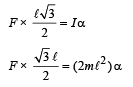
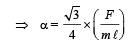
The total force acting on the system along x-direction is F + (Fnet)x
This force is responsible for giving an acceleration ax to the system.
Therefore,
F + (Fnet)x = 3m (ax) c.m.
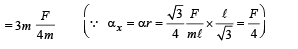

(Fnet)y remains the same as before = √3mlω2.
Q.20. A wooden log of mass M and length L is hinged by a frictionless nail at O. A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision about O.
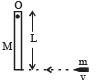
Ans.
Solution. We know that 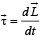
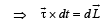
When angular impulse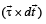 is zero, the angular momentum is constant. In this case for the wooden log-bullet system, the angular impulse about O is constant.
is zero, the angular momentum is constant. In this case for the wooden log-bullet system, the angular impulse about O is constant.
Therefore,
[angular momentum of the system]initial
= [angular momentum of the system]final
⇒ mv × L = I0 × ω ... (i)
where I0 is the moment of inertia of the wooden log-bullet system after collision about O

From (i) and (ii)
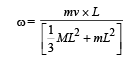
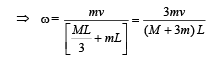
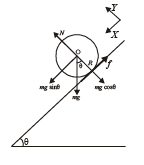
Q.21. A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
Ans. a =2/3 gsinθ
Solution. Applying Fnet = ma in X-direction mg sinθ – f = ma ... (i)
The torque about O will be τ = f × R
= Iα ... (ii)
As the case is of rolling
∴ a = αR

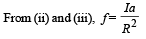
Substituting this value in (i), we get
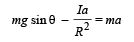
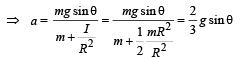
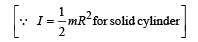
Q.22. Two identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. If the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
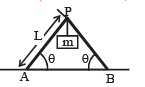
Ans.
Solution.
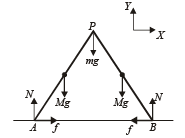
The various forces acting on the ladders are shown in the figure.
Since the system is in equilibrium, therefore ∑Fy = 0
⇒ Mg + mg + Mg = N + N
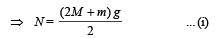
Considering the rotational equilibrium of one ladder as shown in figure. Calculating torques about P
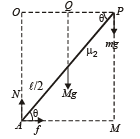
Mg × PQ + f × PM = N × OP
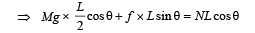
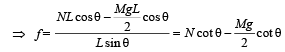
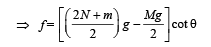
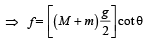
Q.23. A rectangular plate of mass M and dimension a × b is held in horizontal position by striking n small balls (each of mass m) per unit area per second. The balls are striking in the shaded half region of the plate. The collision of the balls with the plate is elastic. What is v?
(Given n = 100, M = 3 kg, m = 0.01 kg; b = 2 m; a = 1 m; g = 10 m/s2).Ans.
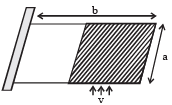
Ans.10 m/s
Solution. KEY CONCEPT Since the plate is held horizontal therefore net torque acting on the plate is zero.
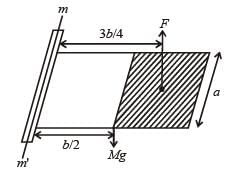
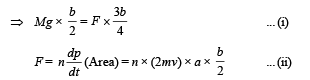
From (i) and (ii)
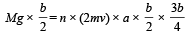
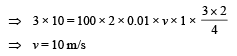
|
481 docs|964 tests
|





















