Subjective Type Questions: Differential Equations | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q. 1. If (a + bx) ey/x = x, then prove that 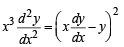
Solution. 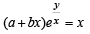
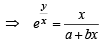 ...(1)
...(1)
Diff. w.r. to x, we get
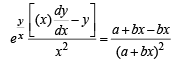
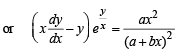 ...(2)
...(2)
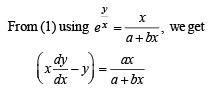
Differentiating (3) w. r. to x, we get
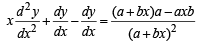
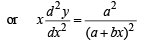
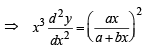 ..(4)
..(4)
Comparing (3) and (4) we get
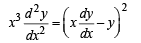
Q. 2. A normal is drawn at a point P(x, y) of a curve. It meets the x–axis at Q. If PQ is of constant length k, then show that the differential equation describing such curves is 
Find the equation of such a curve passing through (0, k).
Solution. The length of normla PQ to any curve y = f (x) is given by
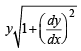
According to question
length of PQ = k
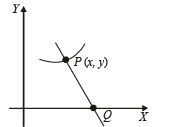
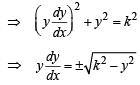
which is the required differential equation of given curve. On solving this D.E. we get the eqn of curve as follows
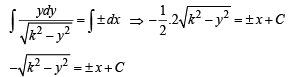
As it passes through (0, k) we get C = 0
∴ Eqn of curve is
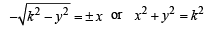
Q. 3. Let y = f (x) be a curve passing through (1, 1) such that the triangle formed by the coordinate axes and the tangent at any point of the curve lies in the first quadrant and has area 2. Form the differential equation and determine all such possible curves.
Ans. x +y = 2 and xy = 1, x,y > 0
Solution. Equation of the tangent to the curve y = f (x) at point
(x,y) is Y - y = f '(x)(X-x) ...(1)
The line (1) meets X-axis at 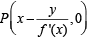 and Y-axis in
and Y-axis in
Q (0, y - xf '(x))
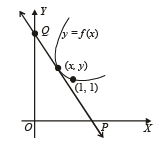
Area of triangle OPQ is
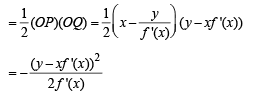
We are given that area of ΔOPQ = 2
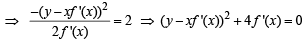
⇒ (y - px)2 + 4p = 0 ...(2)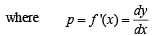
Since OQ > 0, y - xf '(x) > 0. Also note that
p = f '(x)<0
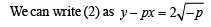
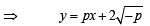 ...(3)
...(3)
Differentiating (3) with respect to x, we get
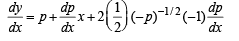
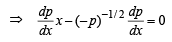
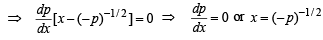
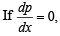 then p = c where c < 0 [∵ p < 0]
then p = c where c < 0 [∵ p < 0]
Putting this value in (3) we get
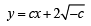 ...(4)
...(4)
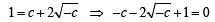
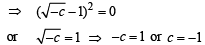
Putting the value of c in (4), we get
y = -x + 2, or x +y= 2
Next, putting x = (- p)-1/ 2 or - p = x-2 in (3) we get
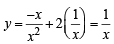
⇒ x y = 1(x > 0,y > 0)
Thus, the two required curves are x +y= 2 and xy = 1, ( x > 0,y> 0).
Q. 4. Determine the equation of the curve passing through the origin, in the form y = f (x), which satisfies the differential equation 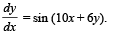
Ans. 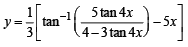
Solution. Put 10 x +6 y = v
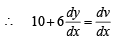

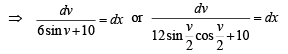
Divide numerator and denomenator by 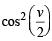 and put
and put 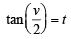
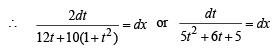
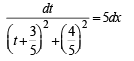
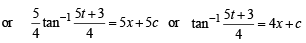
At origin x = 0,y = 0
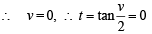
Hence, from above
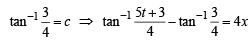
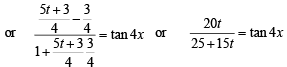
or 4t = (5 + 3t) tan 4x or t (4 - 3 tan 4 x) = 5 tan 4x
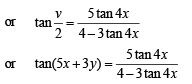
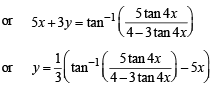
Q. 5. Let u(x) and v(x) satisfy the differential equation 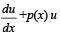
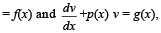 where p(x) f(x) and g(x) are continuous functions. If u(x1) > v(x1) for some x1 and f(x) > g(x) for all x > x1, prove that any point (x, y) where x > x1, does not satisfy the equatons y = u(x) and y = v(x).
where p(x) f(x) and g(x) are continuous functions. If u(x1) > v(x1) for some x1 and f(x) > g(x) for all x > x1, prove that any point (x, y) where x > x1, does not satisfy the equatons y = u(x) and y = v(x).
Solution. (i) y = u (x) and y = v(x) are solutions of given differential equations.
(ii) u (x1) > v(x1) for some x1
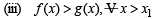
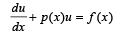
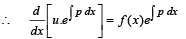
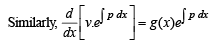
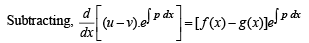
From above since 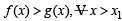 and exponential function is always +ive, then R.H.S. is +ive.
and exponential function is always +ive, then R.H.S. is +ive.
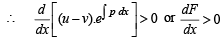
Hence the function 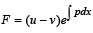 is an increasing function.
is an increasing function.
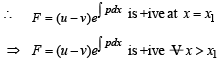
(F being increasing function)
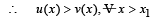
∴ Hence there is no point (x,y) such that x > x1 which can satisfy the equations.
y = u (x) and y = v(x).
Q. 6. A curve passing through the point (1, 1) has the property that the perpendicular distance of the origin from the normal at any point P of the curve is equal to the distance of P from the x–axis. Determine the equation of the curve.
Ans. x2 + y2 – 2 x = 0,x - 1 = 0
Solution. Equation of normal is 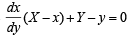
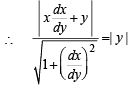
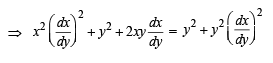
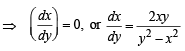
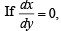 then x = c, when x = 1, y = 1,c= 1.
then x = c, when x = 1, y = 1,c= 1.
∴ x = 1 ...(1)
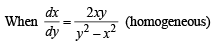

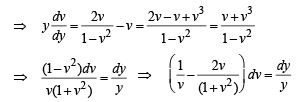
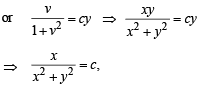
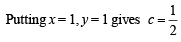
∴ Solution is x2 + y2 - 2x = 0 ...(2)
Hence the solutions are,
x2 + y2 - 2x = 0,x -1 = 0.
Q. 7. A country has a food deficit of 10%. Its population grows continously at a rate of 3% per year. Its annual food production every year is 4% more than that of the last year.
Assuming that the average food requirement per person remains constant, prove that the country will become self– sufficient in food after n years, where n is the smallest integer bigger than or equal to 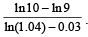
Solution. Let X0 be initial population of the country and Y0 be its initial food production. Let the average consumption be a units. Therefore, food required initially a X0. It is given
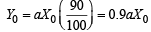 ...(i)
...(i)
Let X be the population of the country in year t.
Then dX/dt = rate of change of population
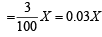
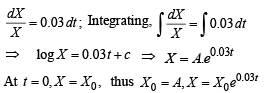
Let Y be the food production in year t.
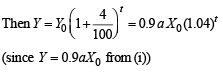
Food consumption in the year t is a X 0e0.03t
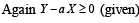
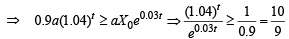
Taking log on both sides,
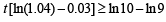
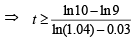
Thus, the least integral value of the year n, when the country becomes self-sufficient, is the smallest integer greater than or equal to 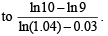
Q. 8. A hemispherical tank of radius 2 metres is initially full of water and has an outlet of 12 cm2 cross–sectional area at the bottom. The outlet is opened at some instant. The flow through the outlet is according to the law v(t) = 0.6 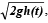 where v(t) and h(t) are respectively the velocity of the flow through the outlet and the height of water level above the outlet at time t, and g is the acceleration due to gravity. Find the time it takes to empty the tank. (Hint : Form a differential equation by relating the decrease of water level to the outflow).
where v(t) and h(t) are respectively the velocity of the flow through the outlet and the height of water level above the outlet at time t, and g is the acceleration due to gravity. Find the time it takes to empty the tank. (Hint : Form a differential equation by relating the decrease of water level to the outflow).
Ans. 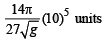
Solution. Let the water level be at a height h after time t, and water level falls by dh in time dt and the corresponding volume of water gone out be dV.
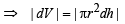 (∵ dh is very small)
(∵ dh is very small)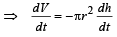 (∵ as t increases, h decreases)
(∵ as t increases, h decreases)
Now, velocity of water, 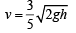
Rate of flow of water = Av (A= 12 cm 2)
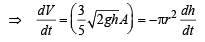
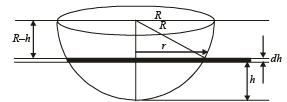
Also from figure,
R2 = (R - h)2+r2 ⇒ r2 = 2hR-h2
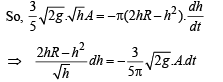
Integrating,
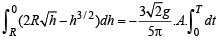
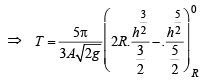
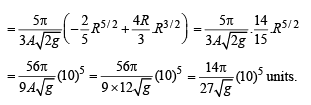
Q. 9. A right circular cone with radius R and height H contains a liquid which evaporates at a rate proportional to its surface area in contact with air (proportionality constant = k > 0).
Find the time after which the cone is empty.
Ans. H/k
Solution. Let at time t, r and h be the radius and height of cone of water.
∴ At time t, surface area of liquid in contact with air = πr2
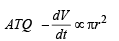
[∵ ‘–’ve sign shows that V decreases with time.]
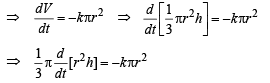
But from figure 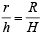 [Using similarity of Δ’s ]
[Using similarity of Δ’s ]
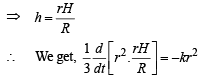
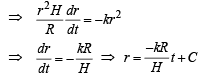
But at t = 0, r = R ⇒ R = 0 + C ⇒ C = R

Now let the time at which cone is empty be T then at T, r = 0 (no liquid is left)
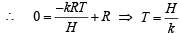
Q. 10. A curve ‘C’ passes thr ough (2, 0) an d the slope at (x, y) as 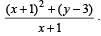 Find the equation of the curve. Find the area bounded by curve and x–axis in fourth quadrant.
Find the equation of the curve. Find the area bounded by curve and x–axis in fourth quadrant.
Ans. 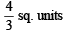
Solution. According to question
slope of curve C at 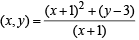
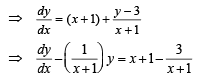
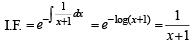
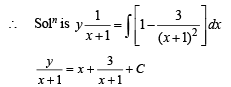
y = x( x + 1) + 3 + C (x+ 1) ...(1)
As the curve passes through (2, 0)
∴ 0 = 2.3 +3 + C.3
⇒ C =-3
∴ Eqn. (1) becomes
y = x(x +1) + 3 - 3x-3
y = x2- 2x ...(2)
which is the required eqn of curve.
This can be written as (x - 1)2 = (y+ 1)
[Upward parabola with vertex at (1, –1), meeting x-axis at (0, 0) and (2, 0)]
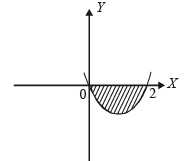
Area bounded by curve and x-axis in fourth quadrant is as shaded region in fig. given by
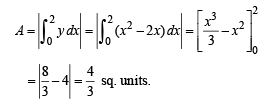
Q. 11. If length of tangen t at any point on the curve y = f(x) intecepted between the point and the x–axis is of length 1. Find the equation of the curve.
Ans. 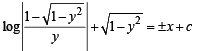
Solution. We know that length of tangent to curve y = f (x) is given by
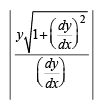
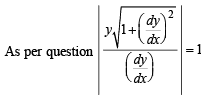
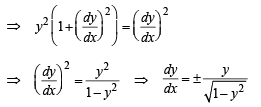
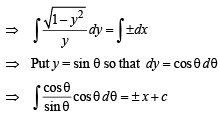
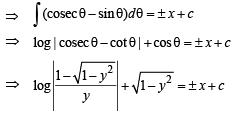
|
347 docs|185 tests
|
FAQs on Subjective Type Questions: Differential Equations - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What is a differential equation? |  |
| 2. What is the importance of differential equations in physics? |  |
| 3. How are differential equations classified? |  |
| 4. What are the techniques used to solve differential equations? |  |
| 5. How are differential equations used in real-life applications? |  |






















