JEE Advanced (Subjective Type Questions): Mechanical Properties of Solids & Fluids | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. A column of mercury of 10 cm length is contained in the middle of a narrow horizontal 1 m long tube which is closed at both the ends. Both the halves of the tube contain air at a pressure of 76 cm of mercury. By what distance will the column of mercury be displaced if the tube is held vertically? (1978)
Ans. 2.95 cm
Solution. M is the mid-point of tube AB.
At equilibrium
p1× A + mg = p2 × A
p1 × A + 10 × A × dHgg = p2 × A
⇒ p1 + 10dHg × g = p2 ... (i)
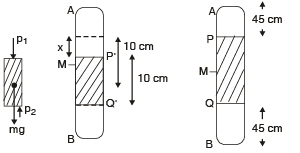
For air present in column AP
p × 45 × A = p1 × (45 + x) × A
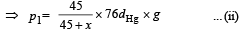
For air present in column QB
p × 45 × A = p2 × (45 – x) × A
From (i), (ii) and (iii)
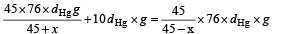
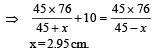
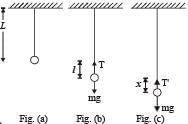
Q.2. A point mass m is suspended at the end of a massless wire of length l and cross section A. If Y is the Young’s modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line. (1978)
Ans.
Solution. From fig. (b), due to equilibrium
T = mg ... (i)
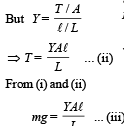
From fig. (c) Restoring force
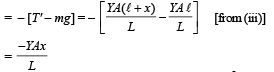
On comparing this equation with F = – mω2x, we get
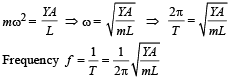
Q.3. A cube of wood supporting 200 gm mass just floats in water. When the mass is removed, the cube ruses by 2cm. What is the size of the cube? (1978)
Ans. l = 10 cm
Solution. Let the edge of cube be ℓ. When mass is on the cube of wood
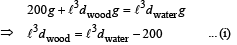
When the mass is removed

From (i) and (ii)
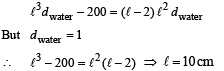
Q.4. A boat floating in a water tank is carrying a number of large stones. If the stones are unloaded into water, what will happen to the water level? (1979)
Ans. Fall
Solution. KEY CONCEPT :
When the stones were in the boat, the weight of stones were balanced by the buoyant force.
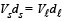
Vℓ, Vs = volume of liquid and stone respectively
dℓ, ds = density of liquid and stone respectively
Since, ds > dℓ ∴ Vs < Vℓ
Therefore when stones are put in water, the level of water falls.
Q.5. A wooden plank of length 1 m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig The tank is filled with water upto a height 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ = 0°) (1984- 8 Marks)
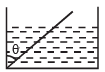
Ans. 45°
Solution. For equilibrium Fnet = 0 and τnet = 0
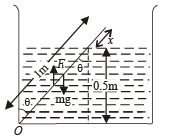
Taking moment about O
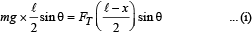
Also FT = wt. of fluid displaced = [(ℓ - x) A] ×ρwg... (ii)
And m = (ℓ A) 0.5ρw ... (iii)
Where A is the area of cross section of the rod.
From (i), (ii) and (iii)
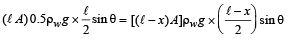
Here, ℓ = 1 m
∴ (1 – x)2 = 0.5 ⇒ x = 0.293 m
From the diagram
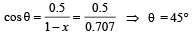
Q.6. A ball of density d is dropped on to a horizontal solid surface. It bounces elastically from the surface and returns to its original position in a time t1. Next, the ball is released and it falls through the same height before striking the surface of a liquid of density of dL (1992 - 8 Marks)
(a) If d < dL, obtain an expression (in terms of d, t1 and dL) for the time t2 the ball takes to come back to the position from which it was released. (b) Is the motion of the ball simple harmonic?
(c) If d = dL, how does the speed of the ball depend on its depth inside the liquid? Neglect all frictional and other dissipative forces. Assume the depth of the liquid to be large.
Ans.
(b) no
(c) remains same
Solution. (a) Let the ball be dropped from a height h. During fall
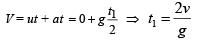
In the second case the ball is made to fall through the same height and then the ball strikes the surface of liquid of density dL. When the ball reaches inside the liquid, it is under the influence of two force (i) Vdg, the weight of ball in downward direction
(ii) VdLg, the upthrust in upward direction.
Note : The viscous forces are absent. (given)
Since, dL > d
the upward force is greater and the ball starts retarding.
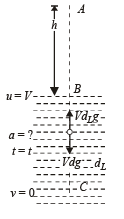
For motion B to C
u = V , v = 0, t = t, a = – a
v = u + at ⇒ 0 = v + (-a)t
⇒ t = v/a
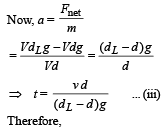
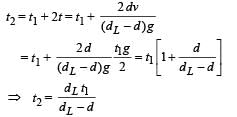
(b) Since the retardation is not proportional to displacement, the motion of the ball is not simple harmonic.
(c) If d = dL then the retardation a = 0. Since the ball strikes the water surface with some velocity, it will continue with the same velocity in downward direction (until it is interrupted by some other force).
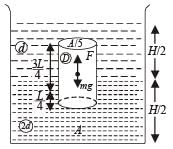
Q.7. A container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
(a) A homogeneous solid cylinder of length L(L < H/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid. Determine:
(i) the density D of the solid and
(ii) the total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area s(s << A) is punched on the vertical side of the container at a height h(h < H/2).
Determine :
(i) the initial speed of efflux of the liquid at the hole,
(ii) the horizontal distance x travelled by the liquid initially, and
(iii) the height hm at which the hole should be punched so that the liquid travels the maximum distance xm initially. Also calculate xm.
(Neglect the air resistance in these calculations.)
Ans.
Solution. (a) (i) KEY CONCEPT :
Since the cylinder is in equilibrium in the liquid therefore Weight of cylinder = upthrust
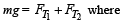
= upth rust due to lower a n d upper liquid respectively
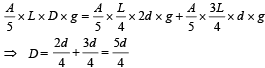
(ii) Total pressure at the bottom of the cylinder = Atmospheric pressure + Pressure due to liquid of density d + Pressure due to liquid of density 2d + Pressure due to cylinder [Weight/Area]
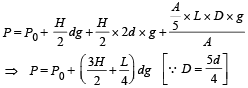
(b) KEY CONCEPT :
Applying Bernoulli's theorem

Horizontal Distance x
ux = v; t = t; x = vt .... (i)
For vertical motion of liquid falling from hole
uy = 0, Sy = h, ay = g, ty = t
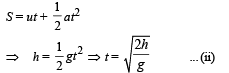
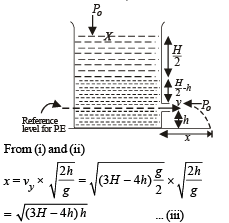
For finding the value of h for which x is maximum, we differentiate equation (iii) w.r.t. t
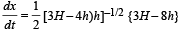
Putting dx/dt = 0 for finding values h for maxima/minima
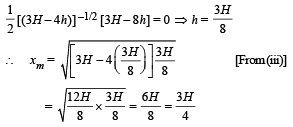
Q.8. A non-viscous liquid of constant density 1000 kg/m3 flows in a streamline motion along a tube of variable cross section.
The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two points P and Q at heights of 2 metres and 5 metres are respectively 4×10–3 m2 and 8×10–3 m2. The velocity of the liquid at point P is 1 m/s. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q. (1997 - 5 Marks)
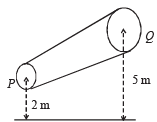
Ans. 29.025 × 103 J/m3 ; 29.4 × 103 J/m.
Solution. Given that
ρ = 1000 kg/m3, h1 = 2m, h2 = 5 m
A1 = 4 × 10–3m2, A2 = 8 × 10–3 m2, v1 = 1 m/s
Equation of continuity
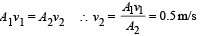
According to Bernoulli's theorem,
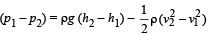
Where (p1 – p2) = work done/vol. [by the pressure]
ρg (h2 – h1) = work done/vol. [by gravity forces]
Now, work done/vol. by gravity forces
= ρg (h2 – h1) = 103 × 9.8 × 3 = 29.4 × 103 J/m3.
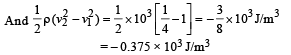
∴ Work done / vol. by pressure
= 29.4 × 103 – 0.375 × 103 J/m3 = 29.025 × 103 J/m3.
Q.9. A unifor m solid cylinder of density 0.8 g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
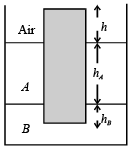
The densities of the liquids A and B are 0.7 g/cm3 and 1.2 g/ cm3, respectively. The height of liquid A is hA = 1.2 cm. The length of the part of the cylinder immersed in liquid B is hB = 0.8 cm.
(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
Ans. (a) zero (b) 0.25 cm (c) g/6,↑
Solution. (a) As the pressure exerted by liquid A on the cylinder is radial and symmetric, the force due to this pressure cancels out and the net value is zero.
(b) For equilibrium, Buoyant force = weight of the body
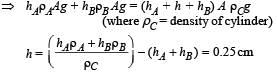
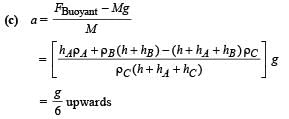
Q.10. A bubble having surface tension T and radius R is formed on a ring of radius b (b << R). Air is blown inside the tube with velocity v as shown. The air molecule collides perpendicularly with the wall of the bubble and stops.
Calculate the radius at which the bubble separates from the ring. (2003 - 4 Marks)

Ans.
Solution. KEY CONCEPT : When the force due to excess pressure in the bubble equals the force of air striking at the bubble, the bubble will detach from the ring.
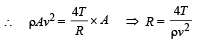
Q.11. Shown in the figure is a container whose top and bottom diameters are D and d respectively. At the bottom of the container, there is a capillary tube of outer radius b and inner radius a.
The volume flow rate in the capillary is Q. If the capillary is removed the liquid comes out with a velocity of v0. The density of the liquid is given as ρ. Calculate the coefficient of viscosity η. (2003 - 4 Marks)
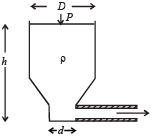
Ans.
Solution. KEY CONCEPT : When the tube is not ther e, using Bernoulli's theorem
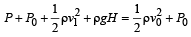
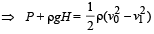
But according to equation of continuity
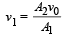
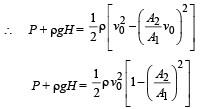
Here, P + ρgH = ΔP According to Poisseuille's equation
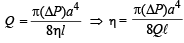
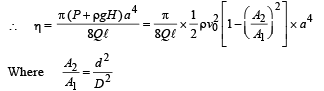
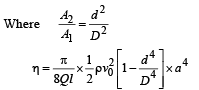
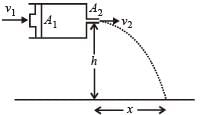
Q.12. A tube has two area of cross-section s as shown in figure. The diameters of the tube are 8 mm and 2 mm. Find range of water falling on horizontal surface, if piston is moving with a constant velocity of 0.25 m/s, h = 1.25 m (g = 10 m/s2) (2004 - 2 Marks)
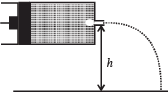 Ans. 2m
Ans. 2m
Solution. From law of continuity A1v1 = A2v2
Given A1 = π × (4 × 10–3 m)2, A2 = π × (1× 10–3 m)2
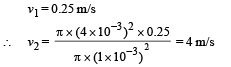
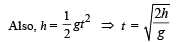
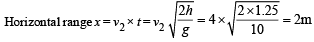
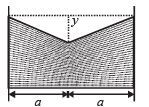
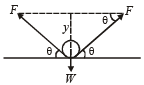
Q.13. A uniform wire having mass per unit length λ is placed over a liquid surface. The wire causes the liquid to depress by y(y << a) as shown in figure. Find surface tension of liquid.
Neglect end effect. (2004 - 2 Marks)
Ans.
Solution. The free body diagram of wire is given below. If ℓ is the length of wire, then for equilibrium 2F sin θ = W.
F = S × ℓ
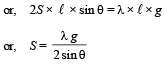
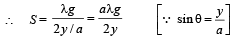
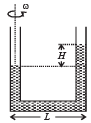
Q.14. A U tube is rotated about one of it’s limbs with an angular velocity ω. Find the difference in height H of the liquid (density ρ) level, where diameter of the tube d << L. (2005 - 2 Marks)
Ans.
Solution. Weight of liquid of height H
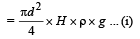
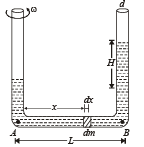
Let us consider a mass dm situated at a distance x from A as shown in the figure. The centripetal force required for the mass to rotate = (dm) xw2
∴ The total centripetal force required for the mass of length L to rotate
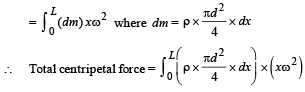
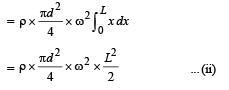
This centripetal force is provided by the weight of liquid of height H.
From (i) and (ii)
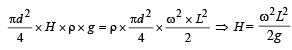
|
481 docs|964 tests
|
















