Surface Area and Volume Exercise 16.2(Part-2) | Extra Documents, Videos & Tests for Class 10 PDF Download

Q-20. A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.

Solution:

Given,

Radius of cylinder (r₁) = 6 cm

Radius of hemisphere (r₂) = 3 cm

Height of cylinder (h) = 15 cm

Height of the cones (l) = 12 cm

Volume of cylinder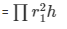 

Volume of each cone = Volume of cone + Volume of hemisphere 

Let, number of cones be ‘n’

n(Volume of each cone) = Volume of cylinder

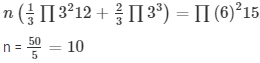
So, the number of cones being filled with the cylinder = n = 10 

Q-21. Consider a solid iron pole having cylindrical portion 110 cm high and the base diameter of 12 cm is surmounted by a cone of 9 cm height. Find the mass of the pole. Assume that the mass of 1 cm³ of iron pole is 8 gm.

Solution:

As per the data given in the question, we have

Base diameter of the cylinder = 12 cm

Radius of the cylinder = 6 cm = r                           (as we know that the radius os half of the diameter)

Height of the cylinder = 110 cm = h

Length of the cone = 9 cm = L

Now,

The volume of the cylinder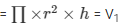 

The volume of the cone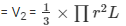  

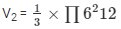
V₂ = 108π cm³

Volume of the pole = volume of the cylinder + volume of the cone = V₁ + V₂ = V

V = 108π + π (6)² 110

V = 12785.14 cm³

Given mass of 1 cm³ of the iron pole = 8 gm

Then, mass of 12785.14 cm³  of the iron pole = 8  12785.14  = 102281.12 gm = 102.2 kg

Therefore, the mass of the iron pole = 102.2 kg

Q-22. A solid toy is in the form of a hemisphere surmounted by a right circular cone. Height of the cone is 2 cm and the diameter of the base is 4 cm. If a right circular cylinder circumscribes the toy, find how much more space it will cover?

Solution:

Given that,

Radius of the cone, cylinder and hemisphere (r) = 2 cm

Height of the cone (l) = 2 cm

Height of the cylinder (h) = 4 cm

Volume of the cylinder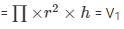

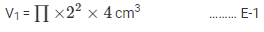
Volume of the cone 

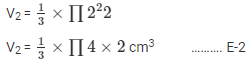
Volume of the hemisphere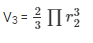 

So, remaining volume of the cylinder when the toy is inserted to it = V₁ – (V₂ + V₃)

V = 16π – 8 π = 8 π cm³

Hence, remaining volume of the cylinder when toy is inserted into it = V = 8 π cm³

Q-23. Consider a solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm, is placed upright in the right circular cylinder full of water such that it touches bottoms. Find the volume of the water left in the cylinder, if radius of the cylinder is 60 cm and its height is 180 cm.

Solution:

As per the data given in the question, we have

Radius of the circular cone = r = 60 cm

Height of the circular cone = L = 120 cm

Radius of the hemisphere = r = 60 cm

Radius of the cylinder = R = 60 cm

Height of the cylinder = H = 180 cm

Now,

Volume of the circular cone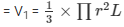

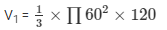
V₁ = 452571.429 cm³

Volume of the hemisphere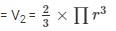

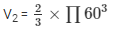
V₂ = 452571.429 cm³ 

Volume of the cylinder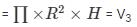 

V₃ = 2036571.43 cm³

Volume of water left in the cylinder = Volume of the cylinder – (volume of the circular cone + volume of the hemisphere ) = V

V = V₃ – (V₁ + V₂)

V = 2036571.43 – (452571.429 + 452571.429)

V = 2036571.43 – 905142.858

V = 1131428.57 cm³

V = 1.1314 m³

Therefore, the volume of the water left in the cylinder = V = 1.1314 m³

Q-24. Consider a cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 8 cm and height 6 cm is completely immersed in water. Find the value of water when :

(i) Displaced out of the cylinder (ii) Left in the cylinder

Solution:

As per the parameters given in the question, we have

Internal diameter of the cylindrical vessel = 10 cm

Radius of the cylindrical vessel = r = 5 cm                                       (as we know that the radius is half of the diameter)

Height of the cylindrical vessel = h = 10.5 cm

Base diameter of the solid cone = 7 cm

Radius of the solid cone = R = 3.5 cm                                                    (as we know that the radius is half of the diameter)

Height of the cone = L = 6 cm

(i) Volume of water displaced out from the cylinder = Volume of the cone = V₁

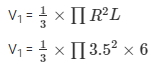
V₁ = 77 cm³

Therefore, the volume of the water displaced after immersion of the solid cone in the cylinder = V₁ =77 cm³

(ii) Volume of the cylindrical vessel =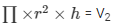

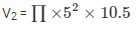
V₂ = 824.6 cm³ = 825 cm³

Volume of the water left in the cylinder = Volume of the cylindrical vessel – Volume of the solid cone

V = V₂ – V₁

V = 825- 77

V = 748 cm³

Therefore, the volume of the water left in cylinder = V = 748 cm³

Q-25. A hemispherical depression is cut from one face of a cubical wooden block of the edge 21 cm such that the diameter of the hemispherical surface is equal to the edge of the cubical surface. Determine the volume and the total surface area of the remaining block.

Solution:

As per the data given in the question itself, we have

Edge of the cubical wooden block = e = 21 cm

Diameter of the hemisphere = Edge of the cubical wooden block = 21 cm

Radius of the hemisphere = 10.5 cm = r                                               (as we know that the radius is half of the diameter)

Now,

Volume of the remaining block = Volume of the cubical block – Volume of the hemisphere

V = 6835.5 cm³ 

Surface area of the block = 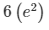 = SA

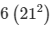SA =           ………………… E-1

Curved surface area of the hemisphere = CSA =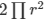 

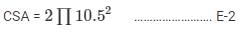
Base area of the hemisphere = BA = 

So, Remaining surface area of the box = SA – (CSA + BA)

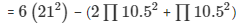
= 2992.5 cm²

Therefore, the remaining surface area of the block = 2992.5 cm²

Volume of the remaining block = V = 6835.5 cm³

Q-26. A boy is playing with a toy which is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21 cm and its volume is 2/3 of the volume of the hemisphere. Calculate the height of the cone and surface area of the toy.

Solution:

As per the parameter given in the question itself, we have

Radius of the cone = 21 cm = R

Radius of the hemisphere = Radius of the cone = 21 cm

Volume of the cone = 2/3 of the hemisphere

We know that,

The volume of the cone = V₁ 

Also, we know that,

The volume of the hemisphere =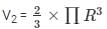

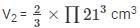
Now, as per the condition 

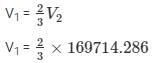
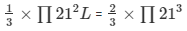
L = 28 cm

Curved surface area of the Cone = CSA₁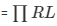 

Curved Surface area of the hemisphere = CSA₂ =  

Now, the total surface area = S = CSA₁ + CSA₂ 

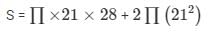
S = 5082 cm²

Therefore, the curved surface area of the toy = S = 5082 cm² 

Q-27. Consider a solid which is in the form of a cone surmounted on hemisphere. The radius of each of them is being 3.5 cm and the total height of the solid is 9.5 cm. Find the volume of the solid.

Solution:

As per the data given in the question, we have

Radius of the hemisphere = 3.5 cm = R

Radius of the cone = Radius of the hemisphere = 3.5 cm = R

Total height of the solid = 9.5 cm = H

Then,

Length of the cone = Total height – Radius of the cone

L = 9.5 – 3.5 = 6 cm

Now,

The volume of the cone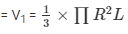

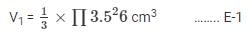
The volume of the hemisphere =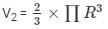 

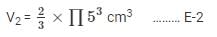
Total volume of the solid = Volume of the cone + Volume of the hemisphere = V

V = V₁ + V₂

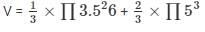
V = 166.75 cm³

So, the volume of the solid = V = 166.75 cm³

Q-28. A wooden toy is made by scooping out a hemisphere of same radius from each end of the solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the volume of the wood in the toy.

Solution:

Given that,

Radius of the cylinder = Radius of the hemisphere = 3.5 cm = r

Height of the hemisphere = 10 cm = h

Volume of the cylinder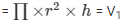

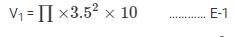
Volume of the hemisphere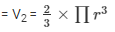 

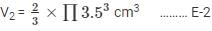
So,

Volume of the wood in the toy = Volume of the cylinder – 2(Volume of the hemisphere)

V = V₁ – V₂

V = 205.33 cm³

Q-29. The largest possible sphere is carved out of a wooden solid cube of side 7 cm. Find the volume of the wood left.

Solution:

Given that,

Diameter of the wooden solid = 7 cm

Radius of the wooden solid = 3.5 cm

Volume of the cube =e³

^{Volume of sphere}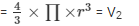 

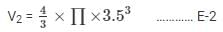
^{Volume of the wood left = Volume of the cube – Volume of sphere} 

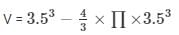
^{V = 163.33 cm3} 

Q-30. From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.

Solution:

Given that,

Height of the cylinder = 2.8 cm = Height of the cone

Diameter of the cylinder = 4.2 cm

Radius of the cylinder = 2.1 cm = Radius of the cone

CSA of the cylindrical part = CSA₁ = 2πRH

CSA₁ = 2π(2.8)(2.1) cm²

Curved surface area of the Cone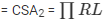

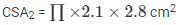
Area of the cylindrical base = πr² = π(2.1)²

Total surface area of the remaining solid = CSA of the cylindrical part + Curved surface area of the Cone + Area of the cylindrical base

TSA = 2π(2.8)(2.1)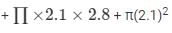 

TSA = 36.96 + 23.1 + 13.86

TSA = 73.92 cm²

Q-31. The largest cone is carved out from one face of the solid cube of side 21 cm. Find the volume of the remaining solid.

Solution:

Given that,

The radius of the largest possible cone is carved out of a solid cube is equal to the half of the side of the cube.

Diameter of the cone = 21 cm

Radius of the cone = 10.5 cm

The height of the cone is equal to the side of the cone.

Volume of the cube = e³

^{Volume of the cone =} 

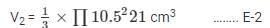
^{Volume of the remaining solid = Volume of cube – Volume of cone} 

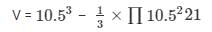
^{V = 6835.5 cm3} 

^{Q-32. A solid wooden toy is in the form of a hemisphere surmounted by a cone of the same radius. The radius of the hemisphere is 3.5 cm and the total wood used in the making of toy is}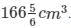   

Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs. 10 per square cm.

Solution:

Given that,

Radius of the hemisphere = 3.5 cm

Volume of the solid wooden toy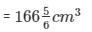

As, Volume of the solid wooden toy = Volume of the cone + Volume of the hemisphere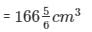  

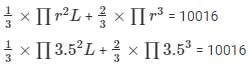
L + 7 = 13

L = 6 cm

Height of the solid wooden toy = Height of the cone + Radius of the hemisphere

= 6 + 3.5

= 9.5 cm

Now, curved surface area of the hemisphere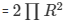

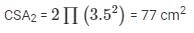
Cost of painting the hemispherical part of the toy = 10 77 = Rs. 770 

Q-33.  How many spherical bullets can be made out of a solid cube of lead whose edge measures 55 cm and each of the bullet being 4 cm in diameter?

Solution:

Let, the total number of bullets be a.

Diameter of the bullet = 4 cm

Radius of the spherical bullet = 2 cm                    (as we know that the radius is half of the diameter)

Now,

Volume of a spherical bullet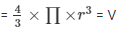 

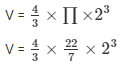
V = 33.5238 cm³

Volume of ‘a’ number of the spherical bullets = V a

V₁ = (33.5238 a) cm²³

Volume of the solid cube = (55)³ = 166375 cm³

Volume of ‘a’ number of the spherical bullets = Volume of the solid cube

33.5238 a = 166375

A = 4962.892

Hence, total number of the spherical bullets = 4963

Q-34. Consider a children’s toy which is in the form of a cone at the top having a radius of 5 cm mounted on a hemisphere which is the base of the toy having the same radius. The total height of the toy is 20 cm. Find the total surface area of the toy.

Solution:

As per the parameters given in the question, we have

Radius of the conical portion of the toy = 5 cm = r

Total height of the toy = 20 cm = h

Length of the cone = L = 20 – 5 = 15 cm

Now,

The curved surface area of the cone = πrL = SA

SA = π (5) (15)

SA = 235.7142 cm²

The curved surface area of the hemisphere = 2πr² = S

S = 2π ( 5 )²

S = 157.1428 cm²

Therefore, The total surface area of the toy = Curved surface area of the cone + curved surface area of the hemisphere = TSA

TSA = 235.7142 + 157.1428

TSA = 392.857 cm²

Hence, the total surface area of the children’s toy = TSA = 392.857 cm²

Q-35.  A boy is playing with a toy conical in shape and is surmounted with hemispherical surface. Consider a cylinder in with the toy is inserted. The diameter of cone is the same as that of the radius of cylinder and hemispherical portion of the toy which is 8 cm. The height of the cylinder is 6 cm and the height of the conical portion of the toy is 3 cm. Assume a condition in which the boy’s toy is inserted in the cylinder, then find the volume of the cylinder left vacant after insertion of the toy.

Solution:

As per the parameter given in the question, we have

Diameter of the cone = Diameter of the Cylinder = Diameter of the Hemisphere = 8 cm

Radius of the cone = Radius of the cylinder = Radius of the Hemisphere = 4 cm = r                        (as we know that the radius is half of the diameter)

Height of the conical portion = 3 cm = L

Height of the cylinder = 6 cm = H

Now,

Volume of the cylinder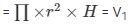

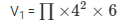
V₁ = 301.7142 cm³

Volume of the Conical portion of the toy =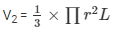

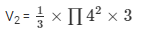
V₂ = 50.2857 cm³

Volume of the hemispherical portion of the toy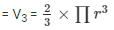

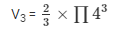
V₃ = 134.0952 cm³

So, the remaining volume of the cylinder when the toy (conical portion + hemispherical portion) is inserted in it = Volume of cylinder – ( volume of the conical portion + volume of the hemispherical portion )

V = V₁ – (V₂ + V₃)

V = 301.7142 – (50.2857 + 134.0952)

V = 301.7142 – 184.3809

V = 117.3333 cm³

Therefore, the remaining portion of the cylinder after insertion of the toy in it = V = 117.3333 cm³

Q-36. Consider a solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm, is placed upright in the right circular cylinder full of water such that it touches bottoms. Find the volume of the water left in the cylinder, if radius of the cylinder is 60 cm and its height is 180 cm.

Solution:

As per the data given in the question, we have

Radius of the circular cone = r = 60 cm

Height of the circular cone = L = 120 cm

Radius of the hemisphere = r = 60 cm

Radius of the cylinder = R = 60 cm

Height of the cylinder = H = 180 cm

Now,

Volume of the circular cone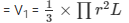

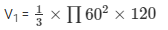
V₁ = 452571.429 cm³

Volume of the hemisphere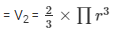

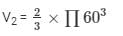
V₂ = 452571.429 cm³

Volume of the cylinder =

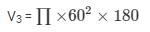
V₃ = 2036571.43 cm³

Volume of water left in the cylinder = Volume of the cylinder – (volume of the circular cone + volume of the hemisphere) = V

V = V₃ – (V₁ + V₂)

V = 2036571.43 – (452571.429 + 452571.429)

V = 2036571.43 – 905142.858

V = 1131428.57 cm³

V = 1.1314 m³

Therefore, the volume of the water left in the cylinder = V = 1.1314 m³

Q-37. Consider a cylindrical vessel with internal diameter 20 cm and height 12 cm is full of water. A solid cone of base diameter 8 cm and height 7 cm is completely immersed in water. Find the value of water when

(i) Displaced out of the cylinder

(ii) Left in the cylinder

Solution:

 As per the parameters given in the question, we have

Internal diameter of the cylindrical vessel = 20 cm

Radius of the cylindrical vessel = r = 10 cm                                       (as we know that the radius is half of the diameter)

Height of the cylindrical vessel = h = 12 cm

Base diameter of the solid cone = 8 cm

Radius of the solid cone = R = 4 cm                                                    (as we know that the radius is half of the diameter)

Height of the cone = L = 7 cm

(i) Volume of water displaced out from the cylinder = Volume of the cone = V₁

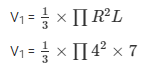
V₁ = 117.3333 cm³

Therefore, the volume of the water displaced after immersion of the solid cone in the cylinder = V₁ =117.3333 cm³

( ii ) Volume of the cylindrical vessel 

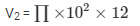
V₂ = 3771.4286 cm³

Volume of the water left in the cylinder = Volume of the cylindrical vessel – Volume of the solid cone

V = V₂ – V₁

V = 3771.4286 – 117.3333

V = 3654.0953 cm³

Therefore, the volume of the water left in cylinder = V = 3654.0953 cm³