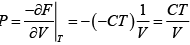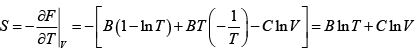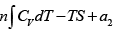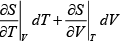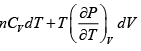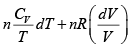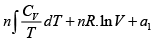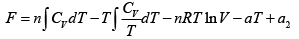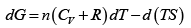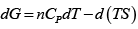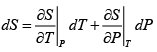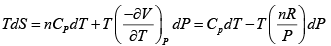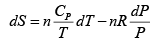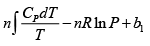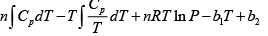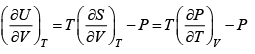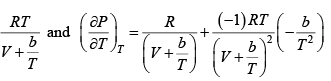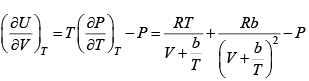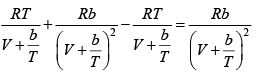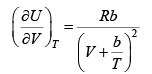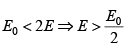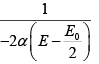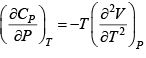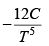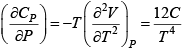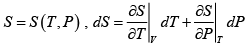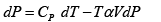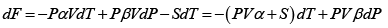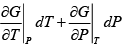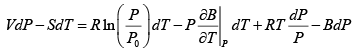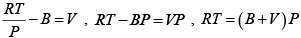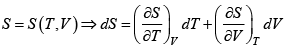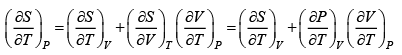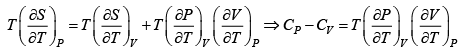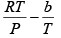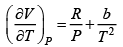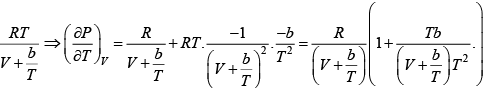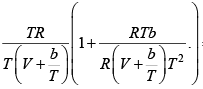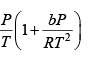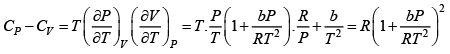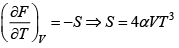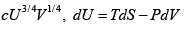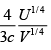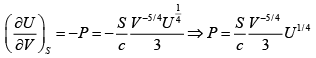Thermodynamical Potential: Assignment | Kinetic Theory & Thermodynamics - Physics PDF Download
Q.1. The Helmholtz free energy of a system given by, F = A+ BT(1-lnT) -CT lnV where A, B,C are constatnt. Obtain expression for pressure, entropy, internal energy, enthalpy and gibbs energy?
dU = TdS- PdV , H = U+ PV , F = U-TS , G = H- TS
dF = -PdV - SdT
Hence,
and
Also U = ( F+ TS )
U = A + BT (1 - ln T) - CT ln V + TB ln T + TC lnV = (A + BT )
H = (U + PV ) = (A+ BT)+CT
G = H - TS = (A+ BT + CT)- TB ln T - TC lnV = A + BT (1- ln T) + CT (1- lnV )
Q.2. Prove that for n -moles of an ideal gas
(a) F = 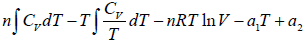
(b) G = 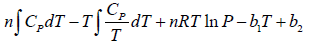
where a1 ,a2 ,b1 and b2 are constant parameter.
(a) F = U- TS , dF = dU- d (TS )
F =
S = S (T ,V)
dS =
TdS =
dS =
S =
(b) G = ( H - TS ) = U + PV - TS
dG = (dU + PdV + VdP) - d (TS ) = dU + nRdT - d (TS )
and S = S (T , P)
S =
Hence, G =
Q.3. If equation of state is given P = 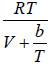
(a) Find the 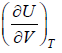
(b) If volume is expanded from V1 to V2 at very high temperature then what will be change in internal energy?
(a)
P =
=
(b) for very high temperature
Q.4. The entropy function of a system is given by S(E) = aE(E0 - E) where a and E0 are positive constants.
(a) For what is condition that energy E temperature is negative .
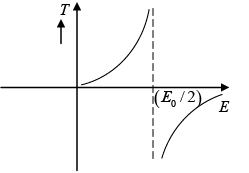
(b) Plot temperature with energy of the system .
(a) From first and second law of thermodynamics
=
⇒ T =
For negative temperature
(b) T =
Q.5. Calculate the Variation of CP with pressure at constant temperature for a substance whose equation of state is given by relation V = 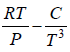
=
Q.6. If α = 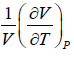 , β =
, β = 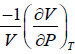 then prove that for an ideal gas prove that
then prove that for an ideal gas prove that
(a) 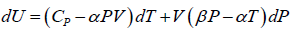
(b) 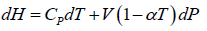
(c) 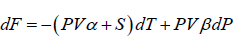
(a) α =
, β =
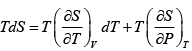
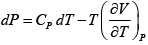
V =
dU =
dU =
(b) H = U+ PV , dH = dU + PdV +VdP = TdS - PdV + PdV +VdPdH = TdS +VdP
S = S (T , P)
dS =
(c) F = (U- TS )
dF = (TdS - PdV) - (TdS + SdT) = -PdV - SdT
and, V = V (T , P)
Q.7. The specific Gibbs energy of an ideal gas is given as-
G = 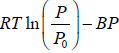
where B is a function of T only obtain the equation of state of gas?
we know that
G =
, dG =
comparing on both sides, we have
Q.8. The equation of state of a gas is given by V = 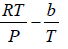
where R is the gas constant and b is another constant parameter. Show that the specific heat at constant pressure CP and the specific heat at constant volume CV for this gas is related by 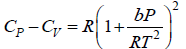
It is given V =
P =
=
=
Q.9. Helmholtz free energy is given by αVT4 where α > 0 .
(a) Find the value of internal energy
(b) For the adiabatic process prove that VT3 = K where K is constant parameter.
(a) U = F+ TS
U =αVT4 + T.4αVT3 = 3αVT4
(b) for adiabatic change dQ = 0 ⇒ TdS = 0, S = constant
= 4αVT3 = constant so VT3 = K
Q.10. For a particular thermodynamic system the entropy S is related to the internal energy U and volume V by 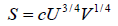
S =
⇒ T =
G = U
= 0
|
6 videos|20 docs|32 tests
|
FAQs on Thermodynamical Potential: Assignment - Kinetic Theory & Thermodynamics - Physics
| 1. What is a thermodynamical potential? |  |
| 2. How is a thermodynamical potential related to equilibrium conditions? |  |
| 3. Can you explain the concept of internal energy as a thermodynamical potential? |  |
| 4. What is the significance of thermodynamical potentials in practical applications? |  |
| 5. How are thermodynamical potentials related to the study of phase transitions? |  |