Tips and Tricks: HCF & LCM | Quantitative Aptitude for SSC CGL PDF Download
HCF and LCM Techniques
The Highest Common Factor (HCF) represents the greatest common divisor of multiple integers. It is essentially the largest positive integer that divides more than one integer. On the other hand, the Least Common Multiple (LCM) pertains to the smallest common multiple of two or more integers. Let's now explore and delve into some of the tips and tricks for HCF and LCM.

HCF and LCM Tips and Tricks and Shortcuts
- The H.C.F of two or more numbers is smaller than or equal to the smallest number of given numbers
- The smallest number which is exactly divisible by a, b and c is L.C.M of a, b, c.
- The L.C.M of two or more numbers is greater than or equal to the greatest number of given numbers.
- The smallest number which when divided by a, b and c leaves a remainder R in each case. Required number = (L.C.M of a, b, c) + R
- The greatest number which divides a, b and c to leave the remainder R is H.C.F of (a – R), (b – R) and (c – R)
- The greatest number which divide x, y, z to leave remainders a, b, c is H.C.F of (x – a), (y – b) and (z – c)
- The smallest number which when divided by x, y and z leaves remainder of a, b, c (x – a), (y – b), (z – c) are multiples of M
- Required number = (L.C.M of x, y and z) – M
Type 1: Tips and Tricks and Shortcuts to find the greatest or smallest number
Example 1: Find the greatest 5 digit number divisible by 5, 15, 20, and 25
(a) 99900
(b) 99000
(c) 99990
(d) 90990
Ans: (a)
LCM of 5, 15, 20, and 25 is 300
The greatest 5 digit number is 99999
99999/300 = 333.33
Type 2: Find the numbers, sum of numbers, product of numbers if
- Their ratio and H.C.F. are given.
- Product of H.C.F. and L.C.M are given
Example 1: The product of two numbers is 3888. If the H.C.F. of these numbers is 36, then the greater number is:
(a) 110
(b) 108
(c) 36
(d) 120
Ans: (b)
Let the two numbers be 36x and 36y
Now, 36x * 36y = 3888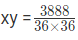
xy = 3
Now, co-primes with product 3 are (1, 3).
Therefore, the required numbers are 36 * 1 = 36
36 * 3 = 108
Therefore the greatest number is 108
Type 3: Tips , Tricks and Shortcuts when sum of two numbers is given , LCM and HCF is given to find the sum of reciprocals.
Example 1: Sum of two numbers is 60 and the H.C.F. and L.C.M. of these numbers are 5 and 100 respectively, then the sum of the reciprocals of the numbers is equals to:
(a) 3/25
(b) 11/220
(c) 21/120
(d) 11/320
Ans: (a)
Let the numbers be a and (b)
Now , given a+b = 60
a × b = HCF × LCM = 5 × 100
= 500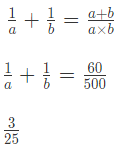
Type 4: How to Solve HCF, LCM Problems related to finding the biggest container to measure quantities
Example 1: Suppose there are three different containers contain different quantities of a mixture of Sugar and rice whose measurements are 403 grams, 434 grams and 465 grams What biggest measure must be there to measure all the different quantities exactly?
(a) 31 grams
(b) 21 grams
(c) 41 grams
(d) 30 litres
Ans: (a)
Prime factorization of 403, 434 and 465 is
403=13×31
434=2×7×31
465=3×5×31
H.C.F of 403, 434 and 465=31
Type 5: Tips , tricks and Shortcuts of HCF, LCM Problems related to Bell ring.
Example 1: Six bells commence tolling together and toll at intervals of 2, 4, 6, 8 10 and 12 seconds respectively. In 30 minutes, how many times do they toll together ?
(a) 8
(b) 16
(c) 9
(d) 10
Ans: (b)
L.C.M. of 2, 4, 6, 8, 10, 12 is 120.
Hence, the bells will toll together after every 120 seconds(2 minutes).
Therefore, in 30 minutes ,number of times bells toll together is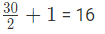
Type 6 : Tips , tricks and Shortcuts of HCF, LCM Problems related to Circle Based Runner Problem.
Example 1: Two people P and Q start running towards a circular track of length 400 m in opposite directions with initial speeds of 10 m/s and 40 m/s respectively. Whenever they meet, P’s speed doubles and Q’s speed halves. After what time from the start will they meet for the third time?
(a) 30 seconds
(b) 26 seconds
(c) 10 seconds
(d) 20 seconds
Ans: (b)
Time taken to meet for the 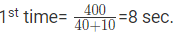
Now P’s speed = 20m/s and Q’s speed=20 m/s.
Time taken to meet for the 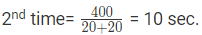
Now P’s speed =40 m/sec and Q’s speed = 10 m/sec.
Time taken to meet for the 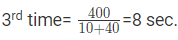
Therefore, Total time= (8+10+8) = 26 seconds.
Tips and Tricks and Shortcuts to find HCF easily
Example 2: Find HCF of 12 and 16.
(a) 5
(b) 4
(d) 12
(d) 16
Ans: (b)
Find the difference between 12 and 16. The difference is 4. Now, check whether the numbers are divisible by the difference. 12 is divisible by 4 and 16 is divisible by 4.Hence, the HCF is 4.
Example 3: Find HCF of 18 and 22.
(a) 2
(b) 4
(c) 18
(d) 36
Ans: (a)
Find the difference between 18 and 22. The difference is 4. Now, check whether the numbers are divisible by the difference. Both 18 and 22 are not divisible by 4. So take the factors of the difference. The factors of 4 are 2*2*1. Now, check whether the numbers are divisible by the factors. 18 and 22 are divisible by factor 2.
Hence, the HCF is 2.
Note: If there are more than two numbers, take the least difference.
Tips and Tricks and Shortcuts to find LCM easily
Example 4: Find LCM of 2,4,8,16.
(a) 16
(b) 18
(c) 12
(d) 2
Ans: (a)
Factorize of above numbe
2 = 2
8 = 23
16 = 24
Choose the largest number. In this example, the largest number is 16. Check whether 16 is divisible by all other remaining numbers. 16 is divisible by 2, 4, 8. Hence, the LCM is 16.
Example 5: Find the LCM of 2,3,7,21.
(a) 21
(b) 44
(c) 36
(d) 42
Ans: (d)
Choose the largest number. The largest number is 21. Check whether 21 is divisible by all other remaining numbers. 21 is divisible by 3 and 7 but not by 2. So multiply 21 and 2. The result is 42. Now, check whether 42 is divisible by 2, 3, 7. Yes, 42 is divisible. Hence, the LCM is 42.
|
315 videos|295 docs|185 tests
|





















