Toroid & Solenoid | Physics for JEE Main & Advanced PDF Download
9. Toroid : It is on hollow circular tube have windings of conducting wire closely attached to each other circularly on it (as shown below)

for ideal Toroid d << R
Magnetic field in Toroid
Let N = Total No. of turns
Now from Ampere's circuital law

B.2πR = μ0 iin = μ0 Ni
⇒ B = 

n =  = No of turns per unit length
= No of turns per unit length
so B = μ0 n i
What is Solenoid?
Let us consider a solenoid, such that its length is large as compared to its radius. Here, the wire is wound in the form of the helix with a very little gap between any two turns. Also, the wires are enameled, thus rendering them insulated from each other. As a result, each turn can be taken as a closed circular loop. The magnetic field thus generated is equivalent to that generated by a circular loop and the total magnetic field generated by the solenoid can be given as the vector sum of force generated by each such turn. The magnetic field lines generated inside a finite solenoid has been shown in the figure below.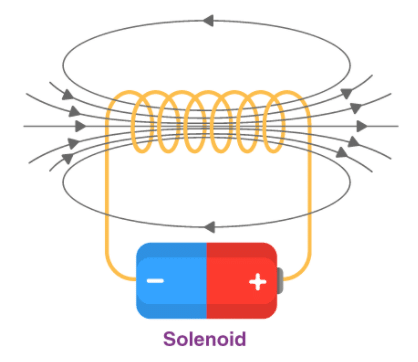
We can see from the figure that the magnetic field inside the solenoid is uniform in nature and is along the axis of the solenoid. The field at the exterior at any point immediately to the solenoid is very weak and the field lines cannot be seen near the close vicinity. It is important to note that the field inside it is parallel to its axis at every position.
From the Ampere’s Law, the magnetic force produced by a solenoid can be given as,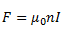
Where n is the number of turns of the wire per unit length, I is the current flowing through the wire and the direction is given using the right-hand thumb rule.
10. Infinite Current Carrying sheet
Now from Ampere's loop



Bl + 0 + Bl + 0 = μ0λ l 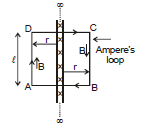
B = 
Ex.14 Three identical long solenoids P, Q and R are connected to each other as shown in figure. if the magnetic field at the center of P is 2.0 T, what would be the field at the centre of Q? Assume that the field due to any solenoid is confined within the volume of that solenoid only.
Sol. 
As the solenoids are identical, the currents in Q and R will be the same and will be half the current in P. The magnetic field within a solenoid is given by B = μ0 ni. Hence the field in Q will be equal to the field in R and will be half the field in P i.e., will be 1.0 T
11. Magnetic force on moving charge
When a charge q moves with velocity  , in a magnetic field
, in a magnetic field  , then the magnetic force experienced by moving charge is given by following formula :
, then the magnetic force experienced by moving charge is given by following formula :
 Put q with sign. ...(9)
Put q with sign. ...(9)
 : Instantaneous velocity
: Instantaneous velocity
 : Magnetic field at that point.
: Magnetic field at that point.
11.1 DIFFERENCE BETWEEN MAGNETIC FORCE AND ELECTRIC FORCE
(1) Magentic force is always perpendicular to the field while electric force is collinear with the field.
(2) Magnetic force is velocity dependent, i.e., acts only when the charged particle is in motion while electric force (qE) is independent of the state of rest or motion of the charged particle.
(3) Magentic force does no work when the charged particle is displaced while the electric force does work in displacing the charged particle.
Note :
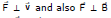
Therefore, 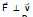 Therefore, power due to magnetic force on a charged particle is zero. (use the formula of power P =
Therefore, power due to magnetic force on a charged particle is zero. (use the formula of power P = 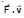 for its proof)
for its proof)
Since the 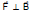 so work done by magnetic force is zero in every part of the motion. The magnetic force cannot increase or decrease the speed (or kinetic energy) of a charged particle. Its can only change the direction of velocity.
so work done by magnetic force is zero in every part of the motion. The magnetic force cannot increase or decrease the speed (or kinetic energy) of a charged particle. Its can only change the direction of velocity.
On a stationary charged particle, magnetic force is zero.
If 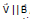 , then also magnetic force on charged particle is zero. It moves along a straight line if only magnetic field is acting.
, then also magnetic force on charged particle is zero. It moves along a straight line if only magnetic field is acting.
Ex.15 A Charged particle of mass 5 mg and charge q = +2μC has velocity  . Find out the magnetic force on the charged particle and its acceleration at this instant due to magnetic field
. Find out the magnetic force on the charged particle and its acceleration at this instant due to magnetic field  .
.  and
and  are in m/s and Wb/m2 respectively.
are in m/s and Wb/m2 respectively.
Sol.  = 2 × 10-6
= 2 × 10-6 
By Newton's Law 
=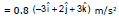
Ex.16 A charged particle has acceleration  in a magnetic field
in a magnetic field  . Find the value of x.
. Find the value of x.
Sol. 

Therefore, 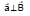
Therefore, 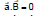
Therefore,  = 0
= 0
⇒ - 6 + 2x = 0 ⇒ x = 3.
12. MOTION OF A CHARGED PARTICLE IN A UNIFORM MAGNETIC FIELD.
12.1 WHEN THE CHARGED PARTICLE IS GIVEN VELOCITY PERPENDICULAR TO THE FIELD
Let a particle of charged q and mass m is moving with a velocity v and enters at right angles to a uniform magnetic field  as shown in figure.
as shown in figure.
The force on the particle is qvB and this force will always act in a direction perpendicular to v. Hence, the particle will move on a circular path. If the radius of the path is r then

 or, r =
or, r =  ...(10)
...(10)
Thus, radius of the path is proportional to the momentum mv of the particle and inversely proportional to the magnitude of magnetic field.
Time period : The time period is the time taken by the charged particle to complete one rotation of the circular path which is given by,
T =  =
=  ...(11)
...(11)
The time period is independent of the speed v.
Frequency : The frequency is number of revolution of charged particle in one second, which is given by,
 ..(12)
..(12)
and angular frequency = 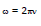
Ex 17. A proton (p), a - particle and deuteron (D) are moving in circular paths with same kinetic energies in the same magnetic field. Find the ratio of their radii and time periods. (Neglect interaction between particles).
Sol. R = 
Therefore, Rp : Ra : RD =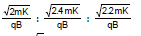
= 1 : 1 : 
T = 2πm/qB
Therefore, Tp : Ta : TD =  :
:  :
: 
= 1 : 2 : 2 Ans.
Ex.18 A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find

(i) time spent,
(ii) distance travelled in the magnetic field
(iii) impulse of magnetic force.
Sol. The particle will move in the field as shown. Angle subtended by the arc at the centre = 2q
(i) Time spent by the charge in magnetic field
wt = q ⇒  ⇒ t =
⇒ t = 
(ii) Distance travelled by the charge in magnetic field :
= r (2θ) = 
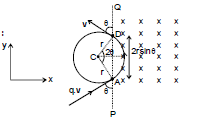
(iii) Impulse = change in momentum of the charge
= (-mv sin θ + mv cos θ  ) - (mv sin θ
) - (mv sin θ  + mv cos θ ) = -2mv sinθ
+ mv cos θ ) = -2mv sinθ
|
293 videos|654 docs|184 tests
|
FAQs on Toroid & Solenoid - Physics for JEE Main & Advanced
| 1. What is a toroid and how does it differ from a solenoid? |  |
| 2. How does a toroid work as an inductor? |  |
| 3. What are some applications of solenoids? |  |
| 4. How does a solenoid create a magnetic field? |  |
| 5. What are some advantages of using toroids and solenoids in electronic systems? |  |






















