Triangles | General Aptitude for GATE - Mechanical Engineering PDF Download
What is a Triangle?
- A triangle is a polygon of three sides.
- Triangles are classified in two general ways: by their sides and by their angles.
Types of Triangle
Based on sides, triangles have been classified into three categories:
- Scalene Triangle: A triangle with three sides of different lengths is called a scalene triangle.
- Isosceles triangle: An isosceles triangle has two equal sides. The third side is called the base. The angles that are opposite to the equal sides are also equal.
- Equilateral triangle: An equilateral triangle has three equal sides. In this type of triangle, the angles are also equal, so it can also be called an equiangular triangle. Each angle of an equilateral triangle must measure 60o, since the sum of the interior angles of any triangle must equal to 180o.

Triangles are also divided into three classes on the basis of measure of the interior angles:
- Obtuse Angled Triangle: When the measure of the largest angle of the triangle is greater than 900 then it is an obtuse angled triangle.
In the figure ΔABC is an obtuse triangle where C is an obtuse angle.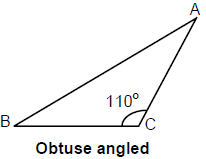
- Acute Angled Triangle: In which all angles are less than 90o e.g.
ΔPQR is an acute triangle because largest angle is less than 90o.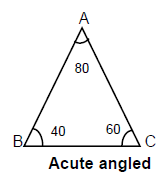
- Right Angled Triangle:
A triangle whose one angle is 90o is called a right (angled) Triangle.
In figure, b is the hypotenuse, and a & c the legs, called base and height respectively.
In right triangle ABC we have,
a2 + b2 = c2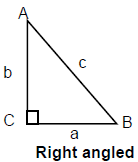

Properties of Triangle
- Sum of the three angles is 180o.
- Sum of exterior angles of any triangle is equal to 360o.
- An exterior angle is equal to the sum of the interior opposite angles.
- The sum of the two sides is always greater than the third side.
- The difference between any two sides is always less than the third side.
- The side opposite to the greatest angle is the greatest side and the side opposite to the smallest angle will be the shortest side.
- If ΔABC is a right-angled triangle then ∠B is equal to 90o unless mentioned otherwise.
- In a right-angled triangle whose angles are 30o, 60o, 90o.
In this triangle side opposite to angle 30o =Hypotenuse
Side opposite to Angle 60o =Hypotenuse.
- Centroid:
(a) The point of intersection of the medians of a triangle. (Median is the line joining the vertex to the
mid-point of the opposite side).
(b) The centroid divides each median from the vertex in the ratio 2 : 1.
(c) To find the length of the median we use the theorem of Apollonius.
AB2 + AC2 = 2(AD2 + BD2)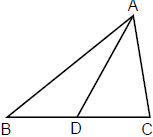
(d) The medians will bisect the area of the triangle.
(e) If x, y, z are the lengths of the medians through A, B, C of a triangle ABC, then
“Four times the sum of the squares of medians is equal to three times the sum of the square of the sides of the triangle”.
4(x2 + y2 + z2) = 3(a2 + b2 + c2). - Orthocentre: This is the point of intersection of the altitudes. (Altitude is a perpendicular drawn from a vertex of a triangle to the opposite side.)
In a right angled triangle, the orthocenter is the vertex, where the right angle is.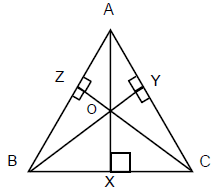
- Circumcentre: It is the point of intersection of perpendicular bisectors of the sides of the triangle.
(a) The Circumcentre of a triangle is the centre of the circle passing through the vertices of a triangle.
(b) The Circumcentre is equidistant from the vertices.
(c) If a, b, c, are the sides of the triangle, Δ is the area, then abc = 4R Δ where R is the radius of the circum-circle.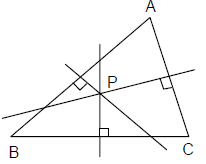
- Incentre: This is the point of intersection of the internal bisectors of the angles of a triangle.
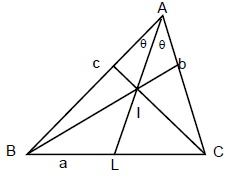
(c) Δ = rs if r is the radius of incircle, where s = semi-perimeter =
and Δ is the area of the triangle.
(d) BF = BD = s – b where 2s = a + b + c,
CE = CD = s – c
AF = AD = s – a
(e) The angle between the internal bisector and the external bisector is 90°.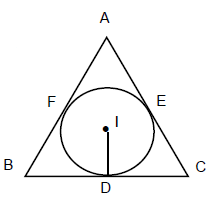
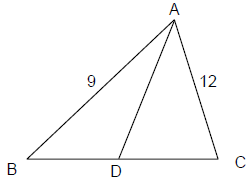
Example.1 In ΔABC, AB = 9, BC = 10, AC = 12. Find the length of median through A.
- In the adjacent figure AD is the required median. Using
- Apollonius theorem in the triangle we have,
2AD2 + 2(5)2 = 81+ 144 .
2AD2 + 50 = 225
Example.2 The sides of the triangle are 6 cm, 8 cm, and 10 cm. Find the area, Inradius and Circumradius of the triangle.
- s =
➢ Equilateral Triangle
In an equilateral triangle, all the sides are equal and all the angles are equal.
(a) Altitude =
(b) Area =
(c) Inradius =
(d) Circumradius =
➢ Congruency
- Two or more figures can be said congruent if and only if they all have same size and shape. If we talk about plane figures then they are congruent if their corresponding sides and angles are equal to the corresponding sides and angles of the other figure.
- Example: Two triangles ABC and DEF are said to the congruent, if they are
equal in all respects (equal in shape and size).
The notation for congruency is ≅ or ≡
➢
Congruent Triangles
- If ∠A =∠D, ∠B = ∠E, ∠C = ∠F
- AB = DE, BC = EF; AC = DF
- Then ΔABC ≡ ΔDEF or ΔABC ≅ ΔDEF
The Tests for Congruency:
(a) SAS Test: Two sides and the included angle of the first triangle are respectively equal to the two sides and included angle of the second triangle.
(b) SSS Test: Three sides of one triangle are respectively equal to the three sides of the other triangle.
(c) ASA Test: Two angles and one side of one triangle are respectively equal to the two angles and one side of the other triangle.
(d) RHS Test: The hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle.
➢
Mid-point Theorem
➢
- A line joining the mid points of any two sides of a triangle must be parallel to the third side and equal to half of that (third side).
- In the adjacent triangle ABC, if D and E are the respective mid-points of sides AB & AC, then DE II BC and DE =
BC

➢
Similar Triangles
➢
- Two figures are said to be similar, if they have the same shape but not necessarily
the same size. If two triangles are similar, the corresponding angles are equal
and the corresponding sides are proportional. - In the figure:
ΔABC ∼ ΔDEF then,
∠A = ∠D, ∠B = ∠E & ∠C = ∠F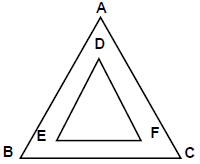

Test for Similarity of Triangles:
(a) AAA Similarity Test: Three angles of one triangle are respectively equal to the three corresponding angles of the other triangle.
(b) SAS Similarity Test: The ratio of two corresponding sides is equal and the angles containing the sides are equal.
(c) SSS Similarity Test: The ratio of all the three corresponding side of the two triangles are equal.
➢
Basic Proportionality Theorem
➢
➢
- In a triangle if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the other two sides proportionally.
- If in ΔABC, DE is drawn parallel to BC, it would divide sides AB and AC proportionally i.e.
Important Result
- If in ΔABC DE II BC, and a line is drawn passing through A and parallel to BC.
Then we will have:
➢
Areas of Similar Triangles
➢
➢
- The ratios of the areas of two similar triangles are equal to the ratio of the square of their corresponding sides i.e. If ΔABC ∼ ΔDEF then
- The ratio of the areas of two similar triangles is also equal to:
(a) Ratio of the square of their corresponding medians.
(b) Ratio of the square of their corresponding Altitudes.
(c) Ratio of the square of their corresponding angle bisectors. - If two triangles are similar, the following properties are true:
(a) The ratio of the medians is equal to the ratio of the corresponding sides.
(b) The ratio of the altitudes is equal to the ratio of the corresponding sides.
(c) The ratio of the internal bisectors is equal to the ratio of the corresponding sides.
➢
Angle Bisector Theorem
➢
➢
➢
- The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle. i.e. In a Δ ABC in which AD is the bisector of ∠A, then
➢
Intercept Theorem
➢
➢
➢
- Intercepts made by two transversals (cutting lines) on three or more parallel lines are proportional.
- In the figure, lines l and m are transversals to three parallel lines AB, CD, EF. Then, the intercepts (portions of lengths between two parallel lines) made, AC, BD & CE, DF, are respectively proportional.
➢
Pythagoras Theorem
➢
➢
➢
➢
- The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides i.e. in a right angled triangle ABC, right angled at C,
- Pythagorean Triplets:
Pythagorean triplets are sets of 3. Integers which can be taken as the three sides
of a right-angled triangle. Few Pythagorean triplets are (3, 4, 5), (5, 12, 13), (7, 24, 25), (9, 40, 41) etc.
➢
Acute Angled Theorem
➢
➢
➢
➢
- In an acute angle triangle ABC, AD is the altitude on BC from vertex A, and ∠ABC is the greatest angle among all the three angles. Then:
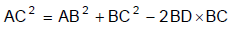
➢
Obtuse Angled Theorem
➢
➢
➢
➢
➢
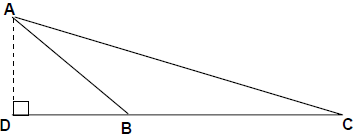
- In an obtuse angle triangle ABC, AD is the altitude on CB produced from vertex A, and ∠ABC is the greatest angle among all the three angles.
- Then AC2 = AB2 + BC2 + 2BD × BC
➢
Apollonius’ Theorem
➢
➢
➢
➢
➢
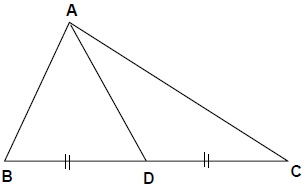
- This theorem is the combination of above two theorems and gives the length of the median. If in ΔABC, AD is the median, meeting side BC at D. Then
|
193 videos|169 docs|152 tests
|
FAQs on Triangles - General Aptitude for GATE - Mechanical Engineering
| 1. What is a triangle? |  |
| 2. What are the types of triangles? |  |
| 3. What are some properties of triangles? |  |
| 4. How do you find the area of a triangle? |  |
| 5. Can a triangle have more than one right angle? |  |