Trigonometric Ratios & Identities | Mathematics (Maths) for JEE Main & Advanced PDF Download
Introduction to Trigonometry
- The word 'trigonometry' is derived from the Greek words 'trigon' and 'metron' and it means 'measuring the sides of a triangle'. The subject was originally developed to solve geometric problems involving triangles. It was studied by sea captains for navigation, surveyor to map out the new lands, by engineers and others.
- Currently, trigonometry is used in many areas such as the science of seismology, designing electric circuits, describing the state of an atom, predicting the heights of tides in the ocean, analysing a musical tone and in many other areas.
Measurement of Angles
There are two systems of measurement of angles:(i) Sexagesimal or English System: Here 1 right angle = 90 (degrees)
1 = 60’ (minutes)
1’ = 60" (seconds)
(ii) Circular System: Here an angle is measured in radians. One radian corresponds to the angle subtended by an arc of length ’r ’ at the centre of the circle of radius r. It is a constant quantity and does not depend upon the radius of the circle.
(a) Relation between the two systems: Degree = Radian*180 / π
(b) If θ is the angle subtended at the centre of a circle of radius 'r',
by an arc of length 'l' then l / r = θ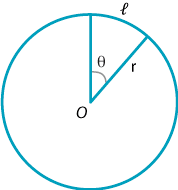
Note: l, r are in the same units and θ is always in radians.
Example.1. If the arcs of the same length in two circles subtend angles of 60° and 75° at their centres. Find the ratio of their radii.
Solution. Let r1 and r2 be the radii of the given circles and let their arcs of the same length s subtend angles of 60 and 75 at their centres.
Now,
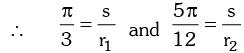
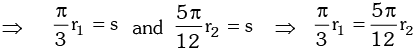
⇒ 4r1 = 5r2 ⇒ r1 : r2 = 5 : 4
T-ratios (or Trigonometric Functions)
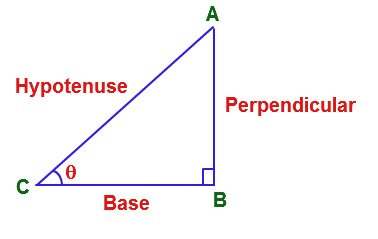
'p' is perpendicular, 'b' is base and 'h' is hypotenuse.
Note : The quantity by which the cosine falls short of unity i.e. 1 - cosθ, is called the versed sine θ of θ and also by which the sine falls short of unity i.e. 1- sinθ is called the coversed sine of θ.
➢ New Definition of T-ratios 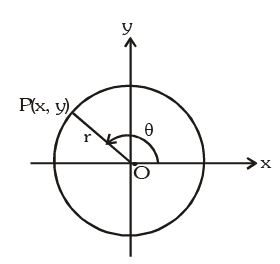 By using rectangular coordinates the definitions of trigonometric functions can be extended to angles of any size in the following way (see diagram). A point P is taken with coordinates (x, y). The radius vector OP has length r and the angle 0 is taken as the directed angle measured anticlockwise from the x-axis.
By using rectangular coordinates the definitions of trigonometric functions can be extended to angles of any size in the following way (see diagram). A point P is taken with coordinates (x, y). The radius vector OP has length r and the angle 0 is taken as the directed angle measured anticlockwise from the x-axis.
The three main trigonometric functions are then defined in terms of r and the coordinates x and y:
- sinθ = y / r
- cosθ = x / r
- tanθ = y / x
(The other function are reciprocals of these)
This can give negative values of the trigonometric functions.
Basic Trigonometric Identities
(i) sin θ. cosec θ = 1
(ii) cos θ. sec θ = 1
(iii) tan θ. cot θ = 1
(iv) tan θ = sin θ / cos θ & cot θ = cos θ / sin θ
(v) sin2 θ + cos2 θ = 1 or sin2 θ = 1 - cos2 θ or cos2 θ = 1 - sin2 θ
(vi) sec2 θ - tan2 θ = 1 or sec2 θ = 1 + tan2 θ or tan2 θ = sec2 θ - 1
(vii) 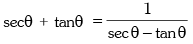
(viii) cosec2 θ - cot2 θ = 1 or cosec2 θ = 1 + cot2 θ or cot2 θ = cosec2 θ - 1
(ix) 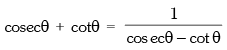
(x) Expressing trigonometrical ratio in terms of each other:
Example.2. If sin θ + sin2 θ = 1 , then prove that cos12 θ + 3 cos10 θ + 3 cos8 θ + cos6 θ - 1 = 0
Solution. Given that sin θ = 1 - sin2 θ = cos2 θ
L.H.S. = cos6 θ (cos2 θ + 1)3 - 1= sin3 θ (1 + sin θ )3 - 1= (sin θ + sin2 θ)3 - 1 = 1 - 1 = 0
Example.3. 2(sin6 θ + cos6 θ) - 3 ( sin4 θ + cos4 θ) + 1 is equal to
(a) 0
(b) 1
(c) –2
(d) none of these
Ans. (a)
Solution. 2 [(sin2 θ + cos2 θ )3 - 3 sin2 θ cos2 θ ( sin2 θ + cos2 θ) ] - 3 [(sin2 θ + cos2 θ)]2 - 2sin2 θ cos2 θ] + 1
= 2 [1 – 3 sin2 θ cos2 θ] - 3 [1 - 2 sin2 θ cos2 θ] + 1
= 2 - 6 sin2 θ cos2 θ - 3 + 6 sin2 θ cos2 θ + 1 = 0
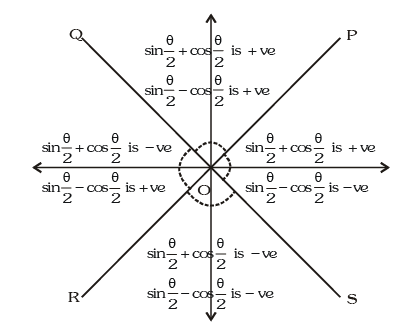
Signs of Trigonometric Functions in Different Quadrants
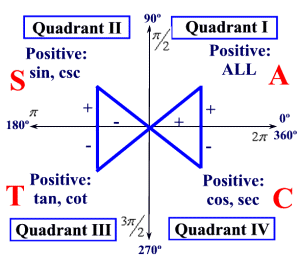
Trigonometric Functions of Allied Angles
(a) sin (2n π + θ) = sin θ, cos (2n π + θ) = cos θ, where n ∈ I
(b)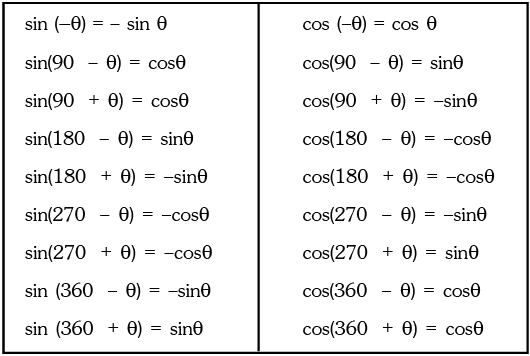
Values of T-ratios of Some Standard Angles
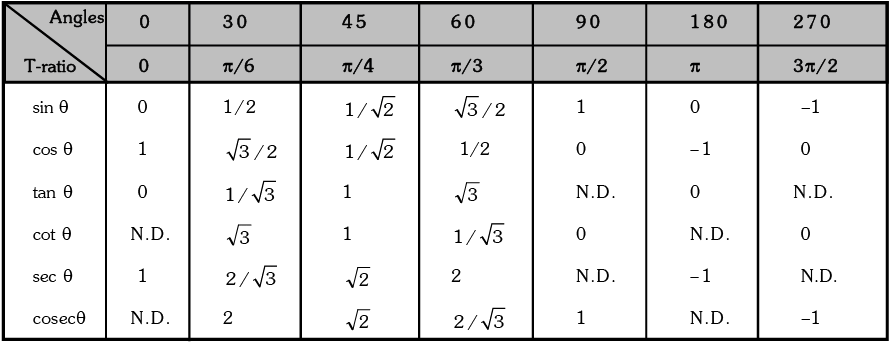
N.D. → Not Defined
(a) sin nπ = 0 ; cos nπ = (-1)n; tan nπ = 0 where n ∈ I
(b) sin(2n + 1) π / 2 = (-1)n; cos(2n + 1) π / 2 = 0 where n ∈ I
Example.4. If sin θ = -1 / 2 and tan θ = 1 / √3 then θ is equal to:
(a) 30°
(b) 150°
(c) 210°
(d) None of these
Ans. (c)
Solution. Let us first find out θ lying between 0 and 360°.
Since sin θ = -1 / 2 ⇒ θ = 210° or 330° and tan θ = 1 / √3 ⇒ θ = 30° or 210°
Hence, θ = 210° or 7π / 6 is the value satisfying both.
Graph of Trigonometric Functions
(i) y = sinx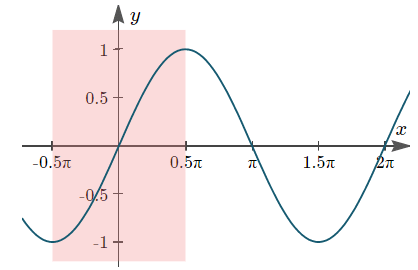
(ii) y = cosx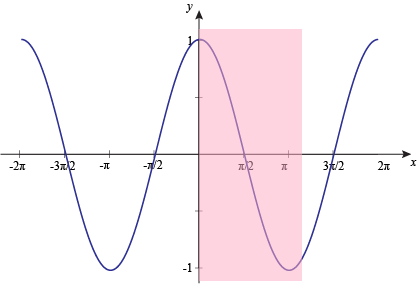
(iii) y = tanx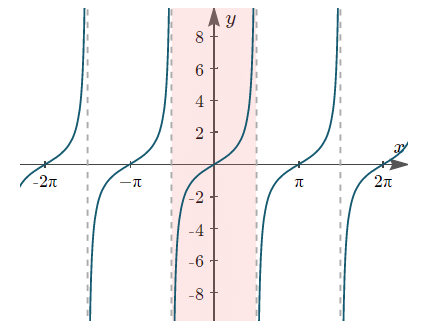 (iv) y = cotx
(iv) y = cotx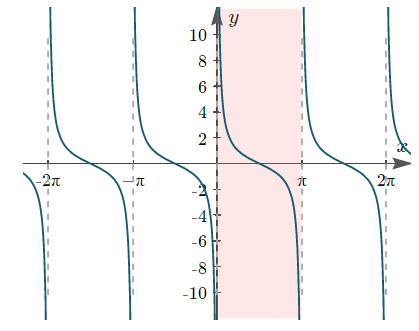 (v) y = secx
(v) y = secx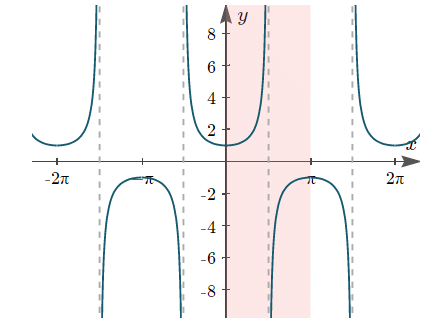
(vi) y = cosecx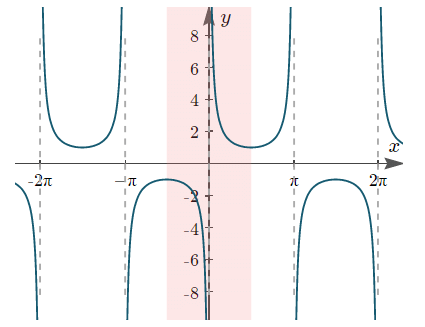
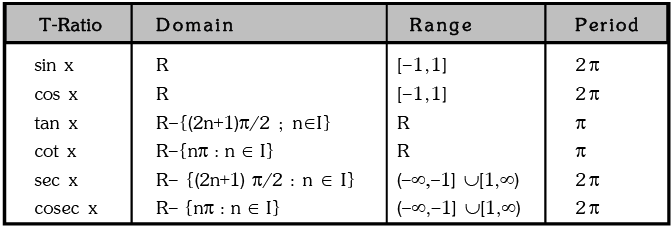
Domains, Ranges and Periodicity of Trigonometric Functions
Trigonometric Ratios of the Sum & Difference of Two Angles
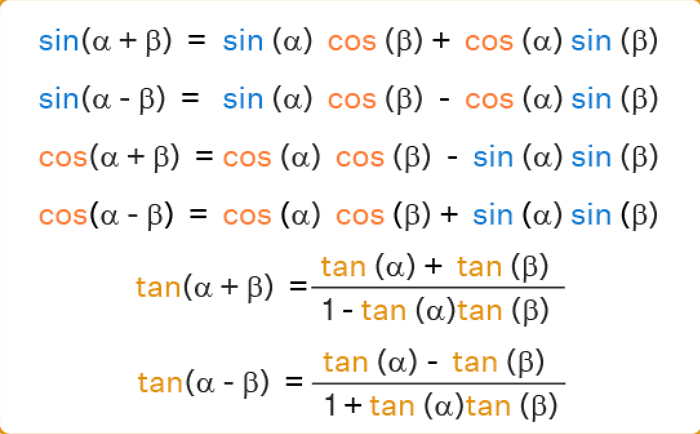
➢ Some More Results
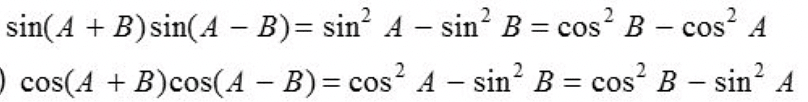
Solved Examples
Example.5. Prove that √3 cosec20° – sec20° = 4.
Solution. L.H.S.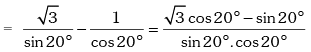
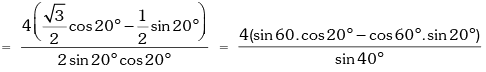
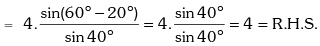
Example.6. Prove that tan70° = cot70° + 2cot40°.
Solution. L.H.S.
= tan70° = tan (20° + 50°)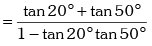
or tan70° – tan20° tan50° tan70° = tan20° + tan50°
or tan70° = tan70° tan50° tan20° + tan20° + tan50° = 2 tan 50° + tan20°
= cot70° + 2cot40° = R.H.S.
Formulas to Transform the Product into Sum or Difference

Example.7. If sin2A = λ sin2B, then prove that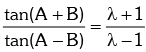
Solution. Given sin2A = λ sin2B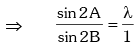
Applying componendo & dividendo,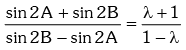
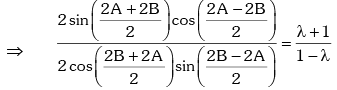
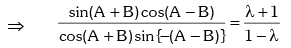
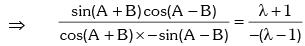
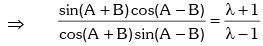
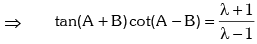
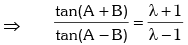
Formulas to Transform Sum or Difference into Product
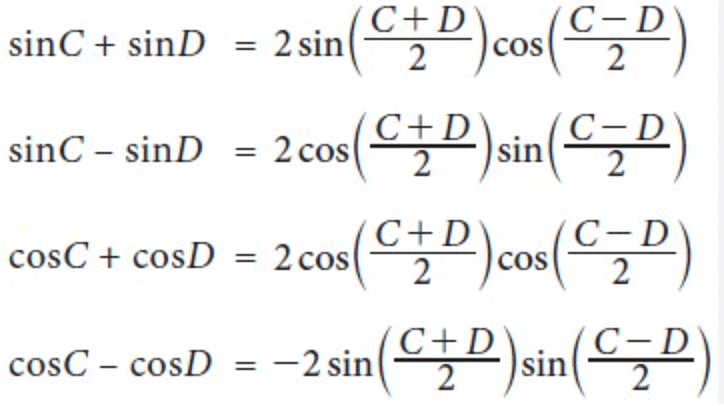
Example.8.
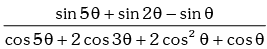 is equal to:
is equal to:(a) tan θ
(b) cos θ
(c) cot θ
(d) none of these
Ans. (a)
Solution. L.H.S.
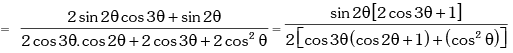
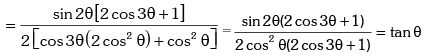
Example.9. Show that sin12º .sin48º .sin54º = 1 / 8
Solution. L.H .S.
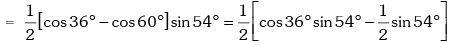
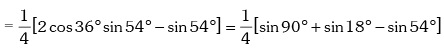
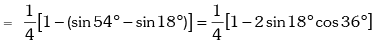
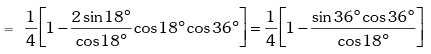
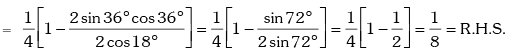
Trigonometric Ratios of sum of more than two angles
(i) sin (A + B + C) = sinAcosBcosC + sinBcosAcosC + sinCcosAcosB – sinAsinBsinC
= ΣsinA cosB cosC – Πsin A
cosA cosB cosC [tanA + tanB + tanC - tanA tanB tanC]
(ii) cos (A + B + C) = cosA cosB cosC – sinA sinB cosC – sinA cosB sinC – cosA sinB sinC
= Πcos A - Σsin A sin B cos C
= cos A cos B cos C [1 - tan A tan B - tan B tan C - tan C tan A]
(iii) tan (A + B + C) =
Trigonometric Ratios of Multiple Angles
(a) Trigonometrical ratios of an angle 2θ in terms of the angle θ :
(i) sin 2θ = 2 sin θ cos θ =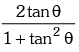
(ii) cos 2θ = cos2θ - sin2θ = 2 cos2θ - 1 = 1 - 2 sin2θ =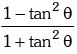
(iii) 1 + cos 2θ = 2 cos2 θ
(iv) 1 - cos 2θ = 2 sin2 θ
(v)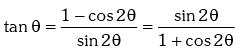
(vi)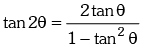
Example.10. Prove that :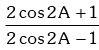 = tan (60º + A) tan (60º - A)
= tan (60º + A) tan (60º - A)
Solution. R.H.S. = tan(60° + A) tan(60° – A)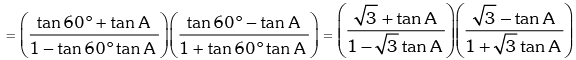
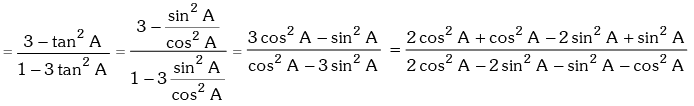
(b) Trigonometrical ratios of an angle 3θ in terms of the angle θ :
(i) sin3θ = 3sinθ - 4sin3θ.
(ii) cos3θ = 4cos3θ - 3cosθ.
(iii)
Example.11. Prove that : tanA + tan(60° + A) + tan(120° + A) = 3tan3A
Solution. L.H.S. = tanA + tan(60° + A) + tan(120° + A)
= tanA + tan(60° + A) + tan{180° –(60° – A)}
= tanA + tan(60° + A) – tan(60° – A) [∵ tan(180° - θ) = -tanθ]

Trigonometric Ratios of Sub Multiple Angles
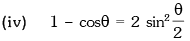
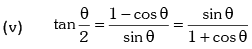
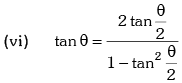
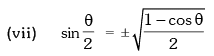
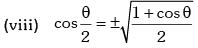
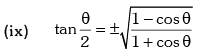
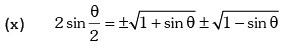
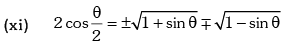
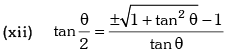
Example.12.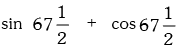 is equal to
is equal to
(a)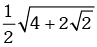
(b)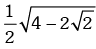
(c)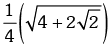
(d)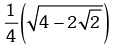
Ans. (a)
Solution. 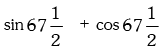
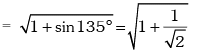
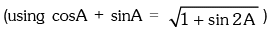
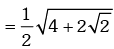
Trigonometric Ratios of Some Standard Angles
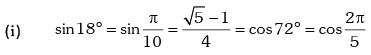
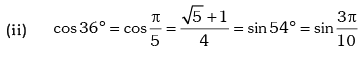
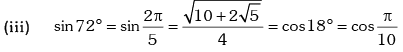
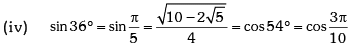
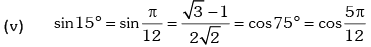
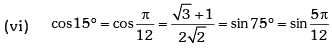
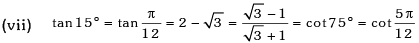
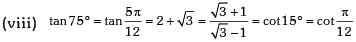
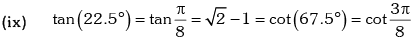

Example.13. Evaluate sin78 ° – sin66 ° – sin42 ° + sin 6°.
Solution. The expression = (sin78° - sin42°) - (sin66° - sin6°) = 2cos(60°) sin(18°) - 2cos36° . sin30°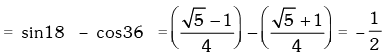
Conditional Trigonometric Identities
If A + B + C = 180°, then
(i) tan A + tan B + tan C = tan A tan B tan C
(ii) cot A cot B + cot B cot C + cot C cot A = 1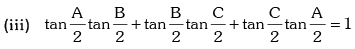
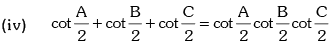
(v) sin 2A + sin 2B + sin 2C = 4 sinA sinB sinC
(vi) cos 2A + cos 2B + cos 2C = –1 – 4 cosA cosB cosC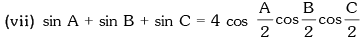
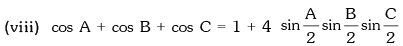
Example.14. In any triangle ABC, sin A – cos B = cos C, then angle B is
(a) π / 2
(b) π / 3
(c) π / 4
(d) π / 6
Ans. (a)
Solution. We have, sin A – cos B = cos C
sin A = cos B + cos C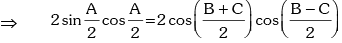
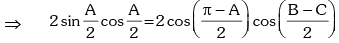 ∵ A + B + C = π
∵ A + B + C = π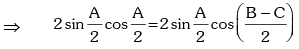
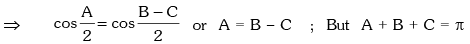
Therefore 2B = π ⇒ B = π / 2
Example.15. If A + B + C = 3π / 2, then cos 2A + cos 2B + cos2C is equal to
(a) 1 – 4cosA cosB cosC
(b) 4 sinA sin B sinC
(c) 1 + 2cosA cosB cosC
(d) 1 – 4 sinA sinB sinC
Ans. (d)
Solution. cos 2A + cos 2B + cos 2C = 2 cos (A + B ) cos (A – B) + cos 2C
=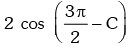 cos (A – B) + cos 2C ∵ A + B + C = 3π / 2
cos (A – B) + cos 2C ∵ A + B + C = 3π / 2
= – 2 sin C cos ( A– B) + 1 – 2 sin2C = 1 – 2 sinC [ cos ( A– B) + sin C)
= 1 – 2 sin C [ cos (A – B) + sin
= 1 – 2 sin C [ cos (A – B) – cos ( A +B ) ]
= 1 – 4 sin A sin B sin C
Maximum & Minimum Values of Trigonometric Expressions
(i) acosθ + bsinθ will always lie in the interval 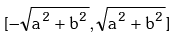 i.e. the maximum and minimum values are
i.e. the maximum and minimum values are 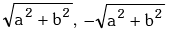 respectively.
respectively.
(ii) Minimum value of a2 tan2 θ + b2 cot2 θ = 2ab where a, b > 0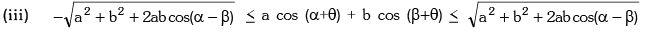 where α and β are known angles.(iv)
where α and β are known angles.(iv)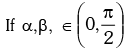 and α + β = s (constant) then
and α + β = s (constant) then
(a) Maximum value of the expression cos α cos β, cos α + cos β, sin α sin β or sin α + sin β occurs when α = β = a / 2
(b) Minimum value of sec α + sec β, tanα + tanβ, cosec α + cosec β occurs when α = β = a / 2
(v) If A, B, C are the angles of a triangle then the maximum value of
sin A + sin B + sin C and sin A sin B sin C occurs when A = B = C = 60
(vi) In case a quadratic in sin θ & cos θ is given then the maximum or minimum values can be obtained by making a perfect square.
Example.16. Prove that: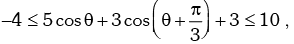 for all values of θ.
for all values of θ.
Solution. We have,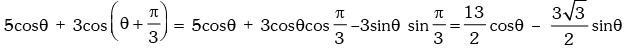
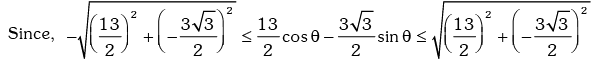
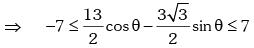
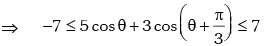 for all θ.
for all θ.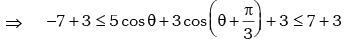 for all θ.
for all θ. for all θ.
for all θ.
Example.17. Find the maximum value of
(a) 1
(b) 2
(c) 3
(d) 4
Ans. (d)
Solution. We have
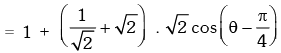
∴ maximum value =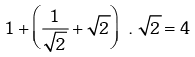
Important Results
(i) sinθ sin (60° – θ) sin (60° + θ) =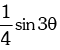
(ii) cosθ. cos (60° - θ) cos (60° + θ) =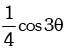
(iii) tanθ tan (60° - θ) tan (60° + θ) = tan 3θ
(iv) cot θ cot (60° - θ) cot (60° + θ) = cot 3θ
(v) (a) sin2 θ + sin2 (60° + θ) + sin2 (60° - θ) = 3 / 2
(b) cos2 θ + cos2 (60° + θ) + cos2 (60° - θ) = 3 / 2
(vi) (a) If tan A + tan B + tan C = tan A tan B tan C, then A + B + C = nπ, n ∈ I
(b) If tan A tan B + tan B tan C + tan C tan A = 1, then A + B + C = (2n + 1) π / 2, n ∈ I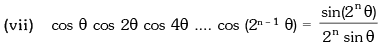
(viii) (a) cotA – tanA = 2cot2A
(b) cotA + tanA = 2cosec2A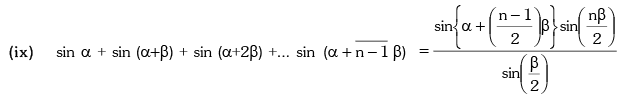
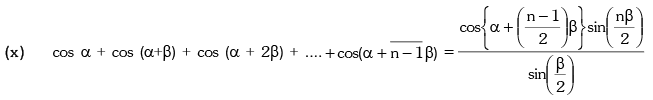
Example.18. Prove that tanA + 2tan2A + 4tan4A + 8cot8A = cot A.
Solution. 8 cot 8A = cotA - tanA - 2tan2A - 4tan4A
= 2 cot2A - 2tan2A - 4tan4A (using viii (a) in above results)
= 4 cot4A - 4tan4A (using viii (a) in above results)
= 8 cot8A.
Alternate Method:
L.H.S. = tanA + 2tan2A + 4tan4A +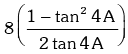
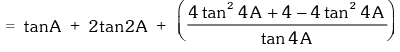
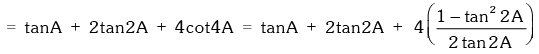
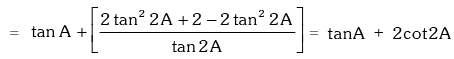
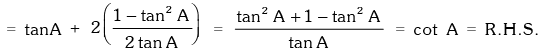
Example.19. Evaluate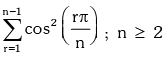
Solution.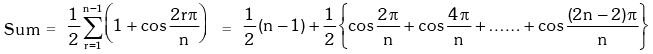

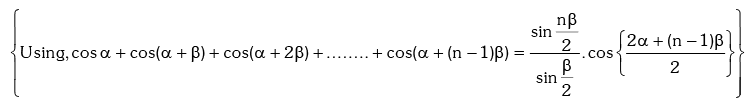
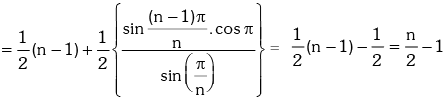
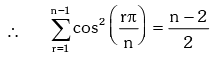
Example.20. Prove that : (1 + sec2θ)(1 + sec22θ)(1 + sec23θ)....(1 + sec2nθ) = tan2nθ.cotθ.
Solution. L.H.S.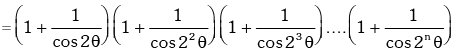
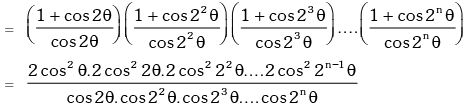

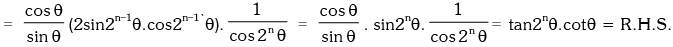
Miscellaneous Illustration
Example.21. Prove that
tanα + 2 tan2α + 22 tan2α + . .. .. . + 2n - 1 tan 2n - 1 α + 2n cot2nα = cot α
Solution. We know tanθ = cotθ - 2 cot 2θ .....(i)
Putting 0 = a, 2α, 22α,.....in (i), we get
tan α = (cot α - 2 cot 2α)
2 (tan 2 α) = 2(cot 2α - 2 cot 22α)
22 (tan 22α) = 22 (cot 22α - 2 cot 23α)
...........................................................
2n - 1 (tan 2n - 1α) = 2n - 1 (cot 2n - 1α - 2 cot 2nα)
Adding,
tan α + 2 tan2α + 22 tan2α +....+ 2n-1 tan 2n-1α = cot a - 2n cot 2nα
∴ tan α + 2 tan2 α + 22 tan2α +....+ 2n-1 tan 2n-1 a + 2n cot 2n a = cot α
Example.22. If A,B,C and D are angles of a quadrilateral and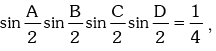 prove that A = B = C = D = π / 2.
prove that A = B = C = D = π / 2.
Solution. 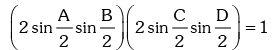
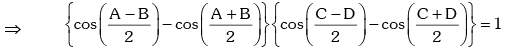
Since, A + B = 2π - (C + D), the above equation becomes,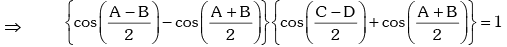
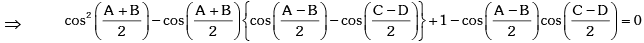
This is a quadratic equation in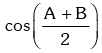 which has real roots .
which has real roots .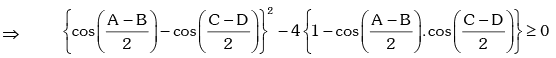
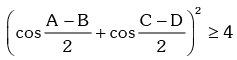

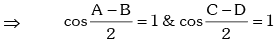
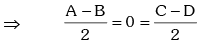
⇒ A = B , C = D .
Similarly A = C, B = D ⇒ A = B = C = D = π / 2
|
172 videos|503 docs|154 tests
|
FAQs on Trigonometric Ratios & Identities - Mathematics (Maths) for JEE Main & Advanced
| 1. What are T-ratios and how are they related to trigonometric functions? |  |
| 2. What are the basic trigonometric identities? |  |
| 3. How do the signs of trigonometric functions vary in different quadrants? |  |
| 4. What are allied angles and how are they related to trigonometric functions? |  |
| 5. What are the domains, ranges, and periodicity of trigonometric functions? |  |
















