Understanding Elementary Shapes Class 6 Notes Maths Chapter 5
Introduction
- Everything we see around us, like shapes and objects, is made up of curves or straight lines.
- These shapes have parts like corners, edges, and surfaces, and they can be open or closed. We can group them into different categories like line segments, angles, triangles, polygons, and circles.
- Each shape has its own size and measurement.
- Now, let’s learn how to compare the sizes of these different shapes.

Measuring Line Segments
A line segment is a part of a line with fixed endpoints, meaning it has a definite length that can be measured.The length of a line segment is a specific number that allows us to compare it with other line segments.
To compare two line segments, we simply compare their lengths, which can be done in different ways.
1. Comparison by observation
By just looking at the line segments we can tell which one is longer.Here we see that line segment AB is longer than CD.
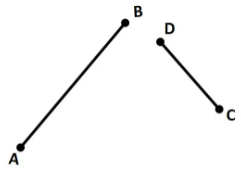
But we can’t tell how much longer, so, we need better methods of comparing line segments.
2. Comparison by tracing
Here, we have to compare AB and CD.

We will use tracing paper this time.
Trace the line segment CD onto the paper and place it over the line segment on AB.
Now, we will be able to decide which is longer. This method depends on the accuracy in tracing the line segment.
But if we want to compare with another line segment you have to trace another line segment. You cannot trace every time you want to compare. So, yet another method was used.
3. Comparison using Ruler and a Divider
 Place the zero mark of the ruler at A. Read the mark against B. This gives the length of AB.
Place the zero mark of the ruler at A. Read the mark against B. This gives the length of AB.
Suppose the length is 5 cm, we may write,
Length AB = 5 cm or more simply as
AB = 5 cm.
Mistakes can happen with this method. The thickness of the ruler might make it hard to read the measurements accurately.
Let us use the divider to measure length.
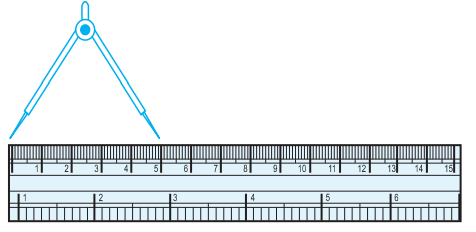
Open the divider.
Place the endpoint of one of its arms at A and the endpoint of the second arm at B.
Now read the mark against the other end point.
Example: Which of the following line-segments is longer?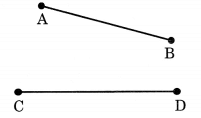
Ans: By using divider, 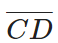 seems greater than
seems greater than 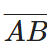 AB¯¯¯¯¯¯
AB¯¯¯¯¯¯
Angles – ‘Right’ and ‘Straight’
Study the following positions: You stand facing north.
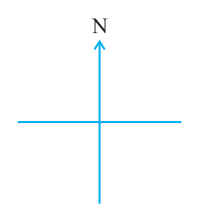
If you turn to the right until you face east, you've made a right-angle turn.
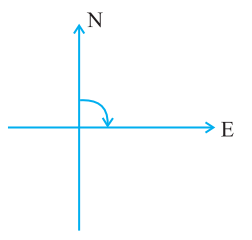
After another right-angle turn to the right, you will now be facing south.
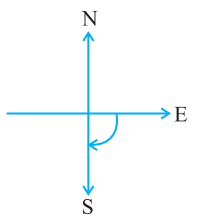
If you turn from north to south, you make a straight angle, which is two right angles.
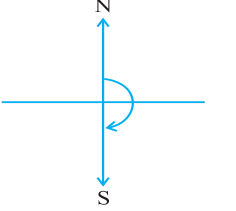
Here, NS is a straight line.
If you turn again from south to north, that's another straight angle. So, after two straight angles, you're back to your original position facing north.
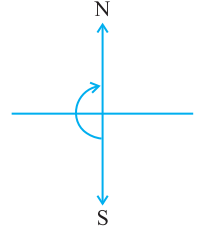
To return to your original position, you need to turn by four right angles, which is one full revolution. The angle for one revolution is a complete angle.
On a clock, if the hand starts at 12 and goes around to 12 again, it has completed one revolution, which equals four right angles.
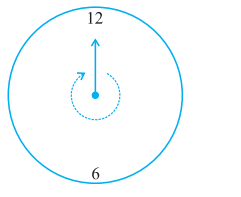
Example 1: How many degrees are there in between the clock hands when it displays 7′0 clock?

Ans: It is 30∘ between any two numbers on the clock.
So, there are 7 divisions between 12 and 7.
Thus, total degrees =7×30∘=210∘
Example 2: How many right angles will you make if you start facing
(a) South(S) and turn clockwise to the West(W)?
(b) North(N) and turn anti-clockwise to the East(E)?
(c) West(W) and turn to West(W)?
(d) South(S) and turn to the North(N)?
Ans: Suppose we revolve one complete round in either a clockwise or anti-clockwise direction. In that case, we will revolve by 360º or four right angles, and the two adjacent directions will be at 90º or one right angle away from each other.
(a) Now, if we start facing South and turn clockwise to West, we make one right angle (90 degrees).
(b) If we start facing North(N) and turn anti-clockwise to East(E), we make three right angles (90 degrees).
(c) If we start facing West(W) and turn to West(W), then we make one complete round or four right angles (90 degrees).
(d) If we start facing South(S) and turn to North(N), then we make two right angles (90 degrees).
Angles – ‘Acute’, ‘Obtuse’ and‘Reflex’
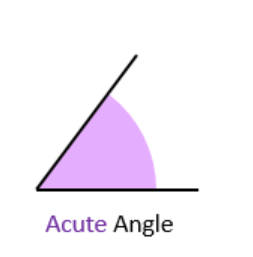
1. Acute Angle
- An angle smaller than a right angle (less than 90 degrees).
- Sharp and pointy. Examples include the angles in an equilateral triangle.
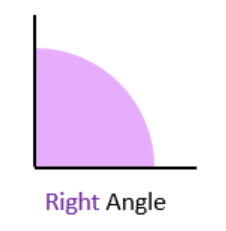
2. Right Angle
- An angle of exactly 90 degrees.
- Forms a perfect "L" shape. Common in corners of squares and rectangles.
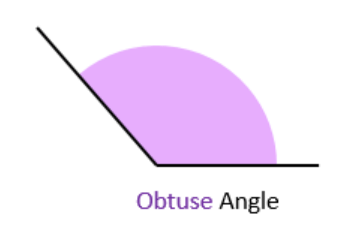
3. Obtuse Angle
- An angle larger than a right angle but smaller than a straight angle (between 90 and 180 degrees).
- Wider than a right angle but not as wide as a straight line.
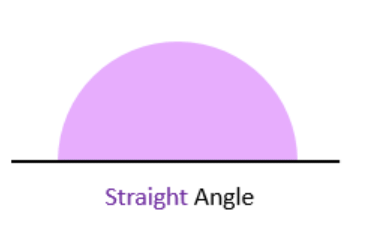
4. Straight Angle
- An angle of exactly 180 degrees.
- Forms a straight line. It is essentially two right angles back-to-back.
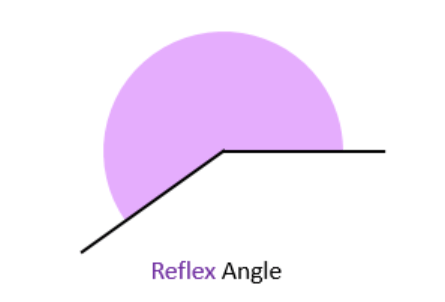
5. Reflex Angle
- An angle larger than a straight angle but less than a full circle (between 180 and 360 degrees).
- Measures more than 180 degrees, often seen in angles that appear to "bend back" on themselves.
Example 1: State the kind of each of the following angles:
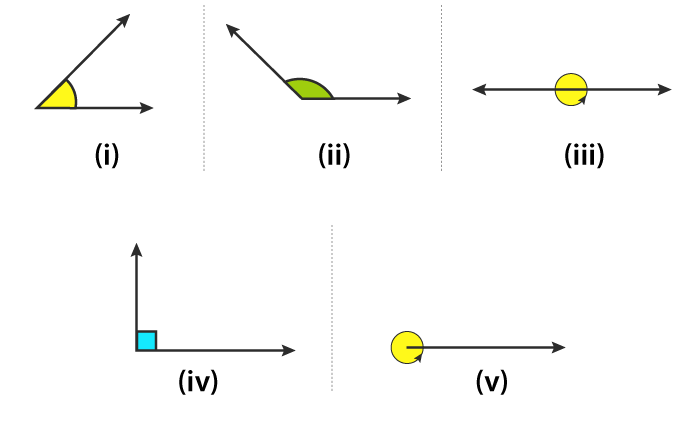
Ans:
(i) Acute angle, which measures between 0o and 90o.
(ii) Obtuse angle, which measures between 90o and 180o.
(iii) Straight angle, which measures 180o.
(iv) Right angle, which measures 90o.
(v) Complete angle, which measures 360o.
Example 2: Classify the following angles as acute, obtuse, straight, right, zero and complete angle:
(i) 118o
(ii) 29o
(iii) 145o
Ans:
(i) 118o is an obtuse angle.
(ii) 29o is an acute angle.
(iii) 145o is an obtuse angle.
How to measure angles?
To measure angles accurately, we use a protractor.

The curved edge is divided into 180 equal parts. Each part is equal to a ‘degree’.
We call our measure, ‘degree measure’.
One complete revolution is divided into 360 equal parts. Each part is a degree.
Let us see how to measure the given angle using a protractor.
- Find the Angle: Place the protractor’s center point at the angle’s vertex.
- Align the Base: Align one side of the angle with the base line of the protractor.
- Read the Measurement: Find where the other side of the angle intersects the protractor’s scale to get the degree measure.
Example:
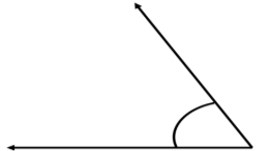
Put the protractor over the angle and you will be get the accurate measure of angle.
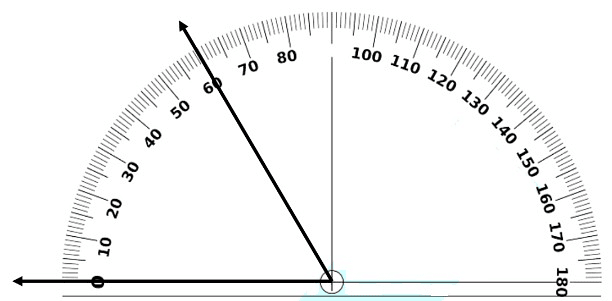
Here, the measure of angle is 60°.
Perpendicular Lines
When two lines intersect and form a right angle (90°) between them, they are called perpendicular. For example, if line AB is perpendicular to line XY, we write it as AB ⊥ XY.Reverse Perpendicularity: If AB ⊥ CD, then CD ⊥ AB as well. Perpendicularity is mutual; the relationship is the same in either direction.
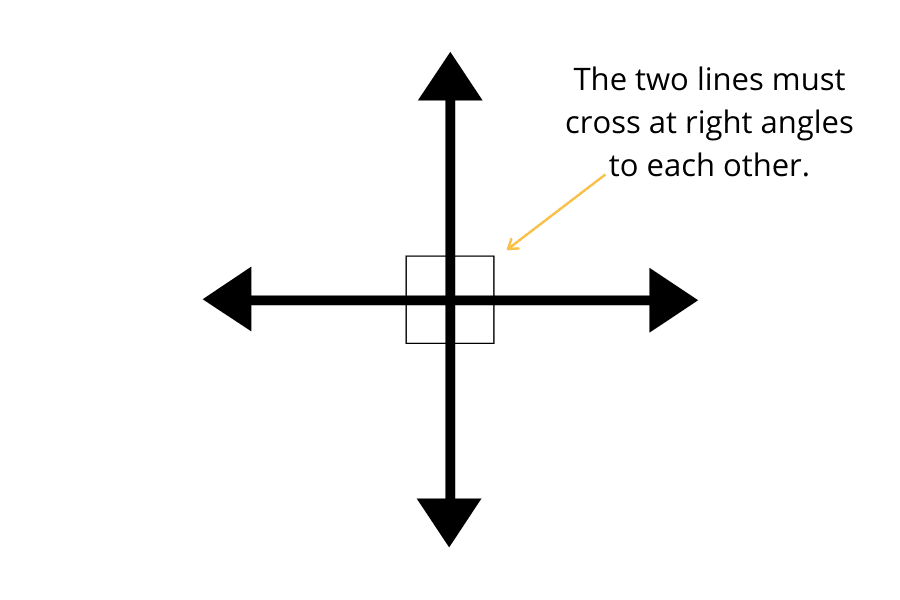
Examples
- English Alphabet: The letter "T" has perpendicular lines. Another example is the letter "F."
- Postcard Edges: The edges of a postcard are perpendicular to each other.
Perpendicular Bisector
If you have a line segment AB and you mark its midpoint M, a line perpendicular to AB at M will divide AB into two equal parts. This line is called the perpendicular bisector of AB.
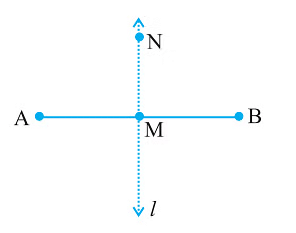
So, a perpendicular bisector not only divides a line segment into two equal parts but also forms a right angle with it.
Classification of Triangles
Triangles can be classified on the basis of
- Sides
- Angles
On the basis of Size
On the basis of side lengths, the triangles are classified into the following types:
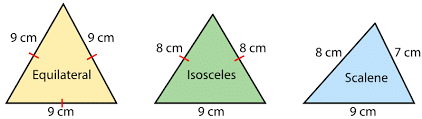
- Equilateral Triangle: A triangle is considered to be an equilateral triangle when all three sides have the same length.
- Isosceles triangle: When two sides of a triangle are equal or congruent, then it is called an isosceles triangle.
- Scalene triangle: When none of the sides of a triangle are equal, it is called a scalene triangle.
Example: What are the types of the following triangles on the basis of sides?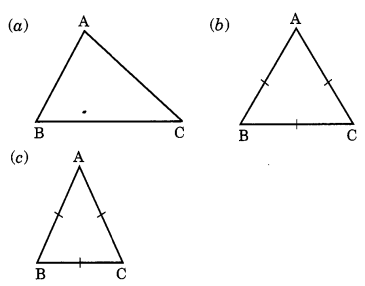
Ans:(a) Scalene triangle.
(b) Equilateral triangle.
(c) Isosceles triangle.
On the basis of Angles
On the basis of angles, triangles are classified into the following types: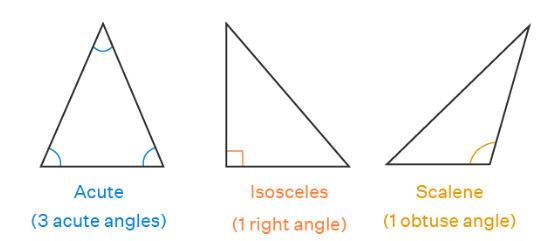
- Acute Triangle: When all the angles of a triangle are acute, that is, they measure less than 90°, it is called an acute-angled triangle or acute triangle.
- Right Triangle: When one of the angles of a triangle is 90°, it is called a right-angled triangle or right triangle.
- Obtuse Triangle: When one of the angles of a triangle is an obtuse angle, that is, it measures greater than 90°, it is called an obtuse-angled triangle or obtuse triangle.
Example: There are five triangles. The measures of some of their angles have been indicated. State for each triangle whether it is acute, right or obtuse.
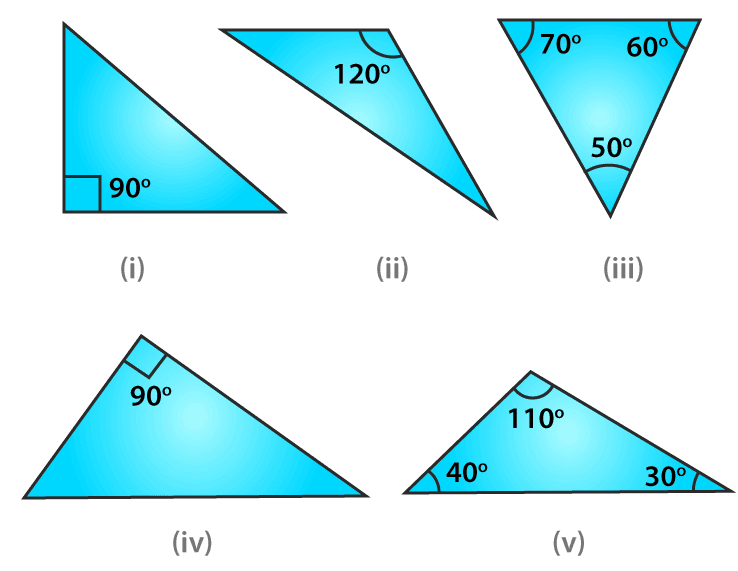
Ans:
(i) It is a right triangle with one angle as 90o.
(ii) It is an obtuse triangle with one angle as 120o.
(iii) It is an acute triangle with one angle as 60o.
(iv) It is a right triangle with one angle as 90o.
(v) It is an obtuse triangle with one angle as 110o.
Quadrilaterals
- A four-sided polygon is a quadrilateral.
- It has 4 sides and 4 angles.
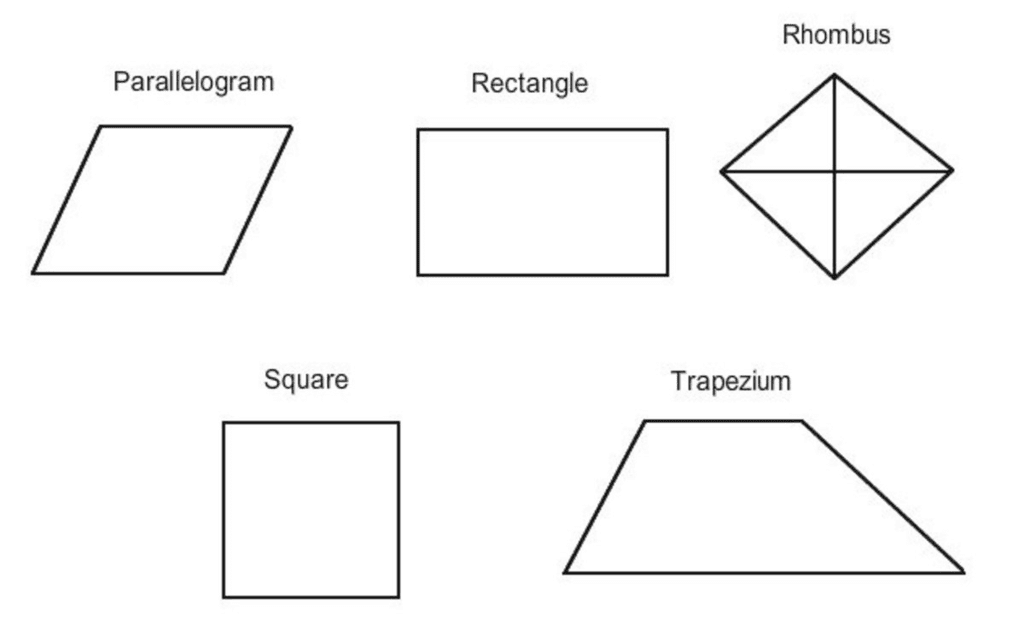
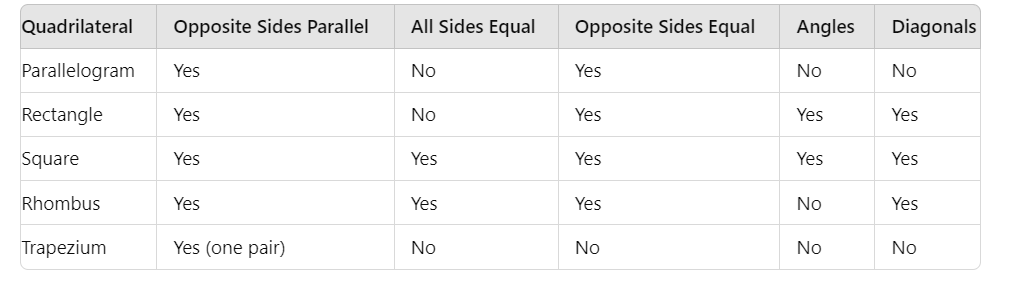
(a) Rectangle: Opposite sides are equal and parallel. Angles are 90°, and diagonals are equal.
(b) Square: All sides are equal. All angles are 90°. Diagonals are equal and perpendicular.
(c) Parallelogram: Opposite sides are parallel and equal. Diagonals are not necessarily equal.
(d) Rhombus: All sides are equal. Opposite angles are equal. Diagonals are perpendicular but not equal.
(e) Trapezium: One pair of opposite sides is parallel.
Example: Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?
Answer: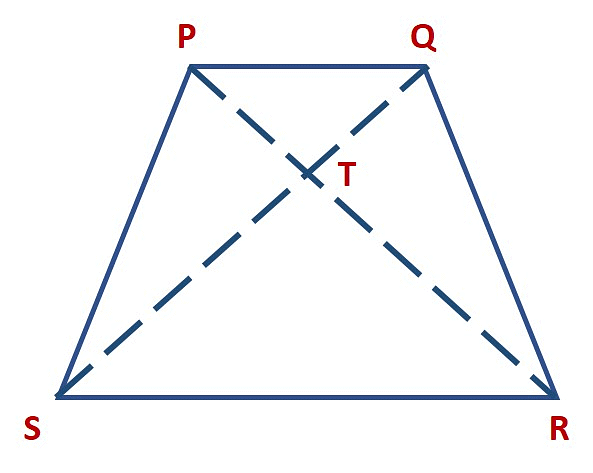
The two diagonals are PR and QS.
Diagonal PR and diagonal QS meet at point T which is in the interior of the quadrilateral PQRS.
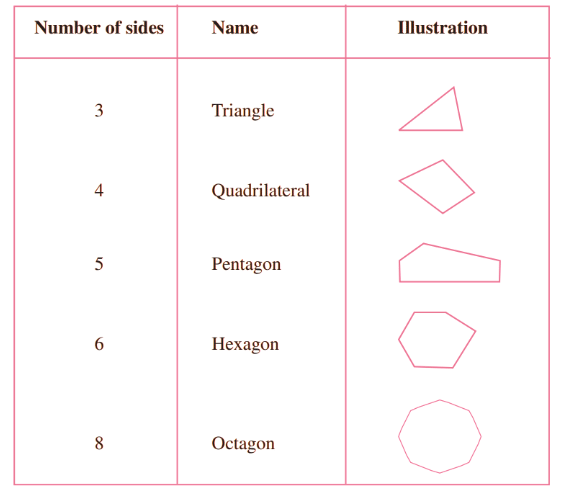
Polygons
A polygon is a closed figure formed of three or more line segments.- Polygons are two dimensional.
- They are bounded by straight lines and the shape is closed.
- Minimum three line segments are required to make a closed figure, thus a triangle is a polygon with a minimum of three sides.
We may classify polygons according to the number of their sides. Let us see some of them:
You can spot many shapes in everyday objects. Rectangles are common in windows, doors, walls, almirahs, blackboards, and floor tiles. They are used because they are easy to make and fit well together. Triangles are also important. You’ll see them in things like bridge supports and roof trusses because they are strong and help hold things up. Triangles are used in many places for their stability and strength.
FAQs on Understanding Elementary Shapes Class 6 Notes Maths Chapter 5
| 1. What are the different types of angles and how are they classified? |  |
| 2. How can I measure line segments accurately? |  |
| 3. What are perpendicular lines and how are they identified? |  |
| 4. How do you classify triangles based on their sides and angles? |  |
| 5. What are polygons and how are they categorized? |  |

















